hypothesis statement in math

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.1: Statements and Conditional Statements

• Last updated
• Save as PDF
• Page ID 7034

• Ted Sundstrom
• Grand Valley State University via ScholarWorks @Grand Valley State University

Much of our work in mathematics deals with statements. In mathematics, a statement is a declarative sentence that is either true or false but not both. A statement is sometimes called a proposition . The key is that there must be no ambiguity. To be a statement, a sentence must be true or false, and it cannot be both. So a sentence such as "The sky is beautiful" is not a statement since whether the sentence is true or not is a matter of opinion. A question such as "Is it raining?" is not a statement because it is a question and is not declaring or asserting that something is true.

Some sentences that are mathematical in nature often are not statements because we may not know precisely what a variable represents. For example, the equation 2\(x\)+5 = 10 is not a statement since we do not know what \(x\) represents. If we substitute a specific value for \(x\) (such as \(x\) = 3), then the resulting equation, 2\(\cdot\)3 +5 = 10 is a statement (which is a false statement). Following are some more examples:

• There exists a real number \(x\) such that 2\(x\)+5 = 10. This is a statement because either such a real number exists or such a real number does not exist. In this case, this is a true statement since such a real number does exist, namely \(x\) = 2.5.
• For each real number \(x\), \(2x +5 = 2 \left( x + \dfrac{5}{2}\right)\). This is a statement since either the sentence \(2x +5 = 2 \left( x + \dfrac{5}{2}\right)\) is true when any real number is substituted for \(x\) (in which case, the statement is true) or there is at least one real number that can be substituted for \(x\) and produce a false statement (in which case, the statement is false). In this case, the given statement is true.
• Solve the equation \(x^2 - 7x +10 =0\). This is not a statement since it is a directive. It does not assert that something is true.
• \((a+b)^2 = a^2+b^2\) is not a statement since it is not known what \(a\) and \(b\) represent. However, the sentence, “There exist real numbers \(a\) and \(b\) such that \((a+b)^2 = a^2+b^2\)" is a statement. In fact, this is a true statement since there are such integers. For example, if \(a=1\) and \(b=0\), then \((a+b)^2 = a^2+b^2\).
• Compare the statement in the previous item to the statement, “For all real numbers \(a\) and \(b\), \((a+b)^2 = a^2+b^2\)." This is a false statement since there are values for \(a\) and \(b\) for which \((a+b)^2 \ne a^2+b^2\). For example, if \(a=2\) and \(b=3\), then \((a+b)^2 = 5^2 = 25\) and \(a^2 + b^2 = 2^2 +3^2 = 13\).

Progress Check 1.1: Statements

Which of the following sentences are statements? Do not worry about determining whether a statement is true or false; just determine whether each sentence is a statement or not.

• 2\(\cdot\)7 + 8 = 22.
• \((x-1) = \sqrt(x + 11)\).
• \(2x + 5y = 7\).
• There are integers \(x\) and \(y\) such that \(2x + 5y = 7\).
• There are integers \(x\) and \(y\) such that \(23x + 27y = 52\).
• Given a line \(L\) and a point \(P\) not on that line, there is a unique line through \(P\) that does not intersect \(L\).
• \((a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3\).
• \((a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3\) for all real numbers \(a\) and \(b\).
• The derivative of \(f(x) = \sin x\) is \(f' (x) = \cos x\).
• Does the equation \(3x^2 - 5x - 7 = 0\) have two real number solutions?
• If \(ABC\) is a right triangle with right angle at vertex \(B\), and if \(D\) is the midpoint of the hypotenuse, then the line segment connecting vertex \(B\) to \(D\) is half the length of the hypotenuse.
• There do not exist three integers \(x\), \(y\), and \(z\) such that \(x^3 + y^2 = z^3\).

Add texts here. Do not delete this text first.

How Do We Decide If a Statement Is True or False?

In mathematics, we often establish that a statement is true by writing a mathematical proof. To establish that a statement is false, we often find a so-called counterexample. (These ideas will be explored later in this chapter.) So mathematicians must be able to discover and construct proofs. In addition, once the discovery has been made, the mathematician must be able to communicate this discovery to others who speak the language of mathematics. We will be dealing with these ideas throughout the text.

For now, we want to focus on what happens before we start a proof. One thing that mathematicians often do is to make a conjecture beforehand as to whether the statement is true or false. This is often done through exploration. The role of exploration in mathematics is often difficult because the goal is not to find a specific answer but simply to investigate. Following are some techniques of exploration that might be helpful.

Techniques of Exploration

• Guesswork and conjectures . Formulate and write down questions and conjectures. When we make a guess in mathematics, we usually call it a conjecture.

For example, if someone makes the conjecture that \(\sin(2x) = 2 \sin(x)\), for all real numbers \(x\), we can test this conjecture by substituting specific values for \(x\). One way to do this is to choose values of \(x\) for which \(\sin(x)\)is known. Using \(x = \frac{\pi}{4}\), we see that

\(\sin(2(\frac{\pi}{4})) = \sin(\frac{\pi}{2}) = 1,\) and

\(2\sin(\frac{\pi}{4}) = 2(\frac{\sqrt2}{2}) = \sqrt2\).

Since \(1 \ne \sqrt2\), these calculations show that this conjecture is false. However, if we do not find a counterexample for a conjecture, we usually cannot claim the conjecture is true. The best we can say is that our examples indicate the conjecture is true. As an example, consider the conjecture that

If \(x\) and \(y\) are odd integers, then \(x + y\) is an even integer.

We can do lots of calculation, such as \(3 + 7 = 10\) and \(5 + 11 = 16\), and find that every time we add two odd integers, the sum is an even integer. However, it is not possible to test every pair of odd integers, and so we can only say that the conjecture appears to be true. (We will prove that this statement is true in the next section.)

• Use of prior knowledge. This also is very important. We cannot start from square one every time we explore a statement. We must make use of our acquired mathematical knowledge. For the conjecture that \(\sin (2x) = 2 \sin(x)\), for all real numbers \(x\), we might recall that there are trigonometric identities called “double angle identities.” We may even remember the correct identity for \(\sin (2x)\), but if we do not, we can always look it up. We should recall (or find) that for all real numbers \(x\), \[\sin(2x) = 2 \sin(x)\cos(x).\]
• We could use this identity to argue that the conjecture “for all real numbers \(x\), \(\sin (2x) = 2 \sin(x)\)” is false, but if we do, it is still a good idea to give a specific counterexample as we did before.
• Cooperation and brainstorming . Working together is often more fruitful than working alone. When we work with someone else, we can compare notes and articulate our ideas. Thinking out loud is often a useful brainstorming method that helps generate new ideas.

Progress Check 1.2: Explorations

Use the techniques of exploration to investigate each of the following statements. Can you make a conjecture as to whether the statement is true or false? Can you determine whether it is true or false?

• \((a + b)^2 = a^2 + b^2\), for all real numbers a and b.
• There are integers \(x\) and \(y\) such that \(2x + 5y = 41\).
• If \(x\) is an even integer, then \(x^2\) is an even integer.
• If \(x\) and \(y\) are odd integers, then \(x \cdot y\) is an odd integer.

Conditional Statements

One of the most frequently used types of statements in mathematics is the so-called conditional statement. Given statements \(P\) and \(Q\), a statement of the form “If \(P\) then \(Q\)” is called a conditional statement . It seems reasonable that the truth value (true or false) of the conditional statement “If \(P\) then \(Q\)” depends on the truth values of \(P\) and \(Q\). The statement “If \(P\) then \(Q\)” means that \(Q\) must be true whenever \(P\) is true. The statement \(P\) is called the hypothesis of the conditional statement, and the statement \(Q\) is called the conclusion of the conditional statement. Since conditional statements are probably the most important type of statement in mathematics, we give a more formal definition.

A conditional statement is a statement that can be written in the form “If \(P\) then \(Q\),” where \(P\) and \(Q\) are sentences. For this conditional statement, \(P\) is called the hypothesis and \(Q\) is called the conclusion .

Intuitively, “If \(P\) then \(Q\)” means that \(Q\) must be true whenever \(P\) is true. Because conditional statements are used so often, a symbolic shorthand notation is used to represent the conditional statement “If \(P\) then \(Q\).” We will use the notation \(P \to Q\) to represent “If \(P\) then \(Q\).” When \(P\) and \(Q\) are statements, it seems reasonable that the truth value (true or false) of the conditional statement \(P \to Q\) depends on the truth values of \(P\) and \(Q\). There are four cases to consider:

• \(P\) is true and \(Q\) is true.
• \(P\) is false and \(Q\) is true.
• \(P\) is true and \(Q\) is false.
• \(P\) is false and \(Q\) is false.

The conditional statement \(P \to Q\) means that \(Q\) is true whenever \(P\) is true. It says nothing about the truth value of \(Q\) when \(P\) is false. Using this as a guide, we define the conditional statement \(P \to Q\) to be false only when \(P\) is true and \(Q\) is false, that is, only when the hypothesis is true and the conclusion is false. In all other cases, \(P \to Q\) is true. This is summarized in Table 1.1 , which is called a truth table for the conditional statement \(P \to Q\). (In Table 1.1 , T stands for “true” and F stands for “false.”)

Table 1.1: Truth Table for \(P \to Q\)

The important thing to remember is that the conditional statement \(P \to Q\) has its own truth value. It is either true or false (and not both). Its truth value depends on the truth values for \(P\) and \(Q\), but some find it a bit puzzling that the conditional statement is considered to be true when the hypothesis P is false. We will provide a justification for this through the use of an example.

Example 1.3:

Suppose that I say

“If it is not raining, then Daisy is riding her bike.”

We can represent this conditional statement as \(P \to Q\) where \(P\) is the statement, “It is not raining” and \(Q\) is the statement, “Daisy is riding her bike.”

Although it is not a perfect analogy, think of the statement \(P \to Q\) as being false to mean that I lied and think of the statement \(P \to Q\) as being true to mean that I did not lie. We will now check the truth value of \(P \to Q\) based on the truth values of \(P\) and \(Q\).

• Suppose that both \(P\) and \(Q\) are true. That is, it is not raining and Daisy is riding her bike. In this case, it seems reasonable to say that I told the truth and that\(P \to Q\) is true.
• Suppose that \(P\) is true and \(Q\) is false or that it is not raining and Daisy is not riding her bike. It would appear that by making the statement, “If it is not raining, then Daisy is riding her bike,” that I have not told the truth. So in this case, the statement \(P \to Q\) is false.
• Now suppose that \(P\) is false and \(Q\) is true or that it is raining and Daisy is riding her bike. Did I make a false statement by stating that if it is not raining, then Daisy is riding her bike? The key is that I did not make any statement about what would happen if it was raining, and so I did not tell a lie. So we consider the conditional statement, “If it is not raining, then Daisy is riding her bike,” to be true in the case where it is raining and Daisy is riding her bike.
• Finally, suppose that both \(P\) and \(Q\) are false. That is, it is raining and Daisy is not riding her bike. As in the previous situation, since my statement was \(P \to Q\), I made no claim about what would happen if it was raining, and so I did not tell a lie. So the statement \(P \to Q\) cannot be false in this case and so we consider it to be true.

Progress Check 1.4: xplorations with Conditional Statements

1 . Consider the following sentence:

If \(x\) is a positive real number, then \(x^2 + 8x\) is a positive real number.

Although the hypothesis and conclusion of this conditional sentence are not statements, the conditional sentence itself can be considered to be a statement as long as we know what possible numbers may be used for the variable \(x\). From the context of this sentence, it seems that we can substitute any positive real number for \(x\). We can also substitute 0 for \(x\) or a negative real number for x provided that we are willing to work with a false hypothesis in the conditional statement. (In Chapter 2 , we will learn how to be more careful and precise with these types of conditional statements.)

(a) Notice that if \(x = -3\), then \(x^2 + 8x = -15\), which is negative. Does this mean that the given conditional statement is false?

(b) Notice that if \(x = 4\), then \(x^2 + 8x = 48\), which is positive. Does this mean that the given conditional statement is true?

(c) Do you think this conditional statement is true or false? Record the results for at least five different examples where the hypothesis of this conditional statement is true.

2 . “If \(n\) is a positive integer, then \(n^2 - n +41\) is a prime number.” (Remember that a prime number is a positive integer greater than 1 whose only positive factors are 1 and itself.) To explore whether or not this statement is true, try using (and recording your results) for \(n = 1\), \(n = 2\), \(n = 3\), \(n = 4\), \(n = 5\), and \(n = 10\). Then record the results for at least four other values of \(n\). Does this conditional statement appear to be true?

Further Remarks about Conditional Statements

Suppose that Ed has exactly $52 in his wallet. The following four statements will use the four possible truth combinations for the hypothesis and conclusion of a conditional statement.

• If Ed has exactly $52 in his wallet, then he has $20 in his wallet. This is a true statement. Notice that both the hypothesis and the conclusion are true.
• If Ed has exactly $52 in his wallet, then he has $100 in his wallet. This statement is false. Notice that the hypothesis is true and the conclusion is false.
• If Ed has $100 in his wallet, then he has at least $50 in his wallet. This statement is true regardless of how much money he has in his wallet. In this case, the hypothesis is false and the conclusion is true.

This is admittedly a contrived example but it does illustrate that the conventions for the truth value of a conditional statement make sense. The message is that in order to be complete in mathematics, we need to have conventions about when a conditional statement is true and when it is false.

If \(n\) is a positive integer, then \((n^2 - n + 41)\) is a prime number.

Perhaps for all of the values you tried for \(n\), \((n^2 - n + 41)\) turned out to be a prime number. However, if we try \(n = 41\), we ge \(n^2 - n + 41 = 41^2 - 41 + 41\) \(n^2 - n + 41 = 41^2\) So in the case where \(n = 41\), the hypothesis is true (41 is a positive integer) and the conclusion is false \(41^2\) is not prime. Therefore, 41 is a counterexample for this conjecture and the conditional statement “If \(n\) is a positive integer, then \((n^2 - n + 41)\) is a prime number” is false. There are other counterexamples (such as \(n = 42\), \(n = 45\), and \(n = 50\)), but only one counterexample is needed to prove that the statement is false.

• Although one example can be used to prove that a conditional statement is false, in most cases, we cannot use examples to prove that a conditional statement is true. For example, in Progress Check 1.4 , we substituted values for \(x\) for the conditional statement “If \(x\) is a positive real number, then \(x^2 + 8x\) is a positive real number.” For every positive real number used for \(x\), we saw that \(x^2 + 8x\) was positive. However, this does not prove the conditional statement to be true because it is impossible to substitute every positive real number for \(x\). So, although we may believe this statement is true, to be able to conclude it is true, we need to write a mathematical proof. Methods of proof will be discussed in Section 1.2 and Chapter 3 .

Progress Check 1.5: Working with a Conditional Statement

The following statement is a true statement, which is proven in many calculus texts.

If the function \(f\) is differentiable at \(a\), then the function \(f\) is continuous at \(a\).

Using only this true statement, is it possible to make a conclusion about the function in each of the following cases?

• It is known that the function \(f\), where \(f(x) = \sin x\), is differentiable at 0.
• It is known that the function \(f\), where \(f(x) = \sqrt[3]x\), is not differentiable at 0.
• It is known that the function \(f\), where \(f(x) = |x|\), is continuous at 0.
• It is known that the function \(f\), where \(f(x) = \dfrac{|x|}{x}\) is not continuous at 0.

Closure Properties of Number Systems

The primary number system used in algebra and calculus is the real number system . We usually use the symbol R to stand for the set of all real numbers. The real numbers consist of the rational numbers and the irrational numbers. The rational numbers are those real numbers that can be written as a quotient of two integers (with a nonzero denominator), and the irrational numbers are those real numbers that cannot be written as a quotient of two integers. That is, a rational number can be written in the form of a fraction, and an irrational number cannot be written in the form of a fraction. Some common irrational numbers are \(\sqrt2\), \(\pi\) and \(e\). We usually use the symbol \(\mathbb{Q}\) to represent the set of all rational numbers. (The letter \(\mathbb{Q}\) is used because rational numbers are quotients of integers.) There is no standard symbol for the set of all irrational numbers.

Perhaps the most basic number system used in mathematics is the set of natural numbers . The natural numbers consist of the positive whole numbers such as 1, 2, 3, 107, and 203. We will use the symbol \(\mathbb{N}\) to stand for the set of natural numbers. Another basic number system that we will be working with is the set of integers . The integers consist of zero, the positive whole numbers, and the negatives of the positive whole numbers. If \(n\) is an integer, we can write \(n = \dfrac{n}{1}\). So each integer is a rational number and hence also a real number.

We will use the letter \(\mathbb{Z}\) to stand for the set of integers. (The letter \(\mathbb{Z}\) is from the German word, \(Zahlen\), for numbers.) Three of the basic properties of the integers are that the set \(\mathbb{Z}\) is closed under addition , the set \(\mathbb{Z}\) is closed under multiplication , and the set of integers is closed under subtraction. This means that

• If \(x\) and \(y\) are integers, then \(x + y\) is an integer;
• If \(x\) and \(y\) are integers, then \(x \cdot y\) is an integer; and
• If \(x\) and \(y\) are integers, then \(x - y\) is an integer.

Notice that these so-called closure properties are defined in terms of conditional statements. This means that if we can find one instance where the hypothesis is true and the conclusion is false, then the conditional statement is false.

Example 1.6: Closure

• In order for the set of natural numbers to be closed under subtraction, the following conditional statement would have to be true: If \(x\) and \(y\) are natural numbers, then \(x - y\) is a natural number. However, since 5 and 8 are natural numbers, \(5 - 8 = -3\), which is not a natural number, this conditional statement is false. Therefore, the set of natural numbers is not closed under subtraction.
• We can use the rules for multiplying fractions and the closure rules for the integers to show that the rational numbers are closed under multiplication. If \(\dfrac{a}{b}\) and \(\dfrac{c}{d}\) are rational numbers (so \(a\), \(b\), \(c\), and \(d\) are integers and \(b\) and \(d\) are not zero), then \(\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}.\) Since the integers are closed under multiplication, we know that \(ac\) and \(bd\) are integers and since \(b \ne 0\) and \(d \ne 0\), \(bd \ne 0\). Hence, \(\dfrac{ac}{bd}\) is a rational number and this shows that the rational numbers are closed under multiplication.

Progress Check 1.7: Closure Properties

Answer each of the following questions.

• Is the set of rational numbers closed under addition? Explain.
• Is the set of integers closed under division? Explain.
• Is the set of rational numbers closed under subtraction? Explain.
• Which of the following sentences are statements? (a) \(3^2 + 4^2 = 5^2.\) (b) \(a^2 + b^2 = c^2.\) (c) There exists integers \(a\), \(b\), and \(c\) such that \(a^2 + b^2 = c^2.\) (d) If \(x^2 = 4\), then \(x = 2.\) (e) For each real number \(x\), if \(x^2 = 4\), then \(x = 2.\) (f) For each real number \(t\), \(\sin^2t + \cos^2t = 1.\) (g) \(\sin x < \sin (\frac{\pi}{4}).\) (h) If \(n\) is a prime number, then \(n^2\) has three positive factors. (i) 1 + \(\tan^2 \theta = \text{sec}^2 \theta.\) (j) Every rectangle is a parallelogram. (k) Every even natural number greater than or equal to 4 is the sum of two prime numbers.
• Identify the hypothesis and the conclusion for each of the following conditional statements. (a) If \(n\) is a prime number, then \(n^2\) has three positive factors. (b) If \(a\) is an irrational number and \(b\) is an irrational number, then \(a \cdot b\) is an irrational number. (c) If \(p\) is a prime number, then \(p = 2\) or \(p\) is an odd number. (d) If \(p\) is a prime number and \(p \ne 2\) or \(p\) is an odd number. (e) \(p \ne 2\) or \(p\) is a even number, then \(p\) is not prime.
• Determine whether each of the following conditional statements is true or false. (a) If 10 < 7, then 3 = 4. (b) If 7 < 10, then 3 = 4. (c) If 10 < 7, then 3 + 5 = 8. (d) If 7 < 10, then 3 + 5 = 8.
• Determine the conditions under which each of the following conditional sentences will be a true statement. (a) If a + 2 = 5, then 8 < 5. (b) If 5 < 8, then a + 2 = 5.
• Let \(P\) be the statement “Student X passed every assignment in Calculus I,” and let \(Q\) be the statement “Student X received a grade of C or better in Calculus I.” (a) What does it mean for \(P\) to be true? What does it mean for \(Q\) to be true? (b) Suppose that Student X passed every assignment in Calculus I and received a grade of B-, and that the instructor made the statement \(P \to Q\). Would you say that the instructor lied or told the truth? (c) Suppose that Student X passed every assignment in Calculus I and received a grade of C-, and that the instructor made the statement \(P \to Q\). Would you say that the instructor lied or told the truth? (d) Now suppose that Student X did not pass two assignments in Calculus I and received a grade of D, and that the instructor made the statement \(P \to Q\). Would you say that the instructor lied or told the truth? (e) How are Parts ( 5b ), ( 5c ), and ( 5d ) related to the truth table for \(P \to Q\)?

Theorem If f is a quadratic function of the form \(f(x) = ax^2 + bx + c\) and a < 0, then the function f has a maximum value when \(x = \dfrac{-b}{2a}\). Using only this theorem, what can be concluded about the functions given by the following formulas? (a) \(g (x) = -8x^2 + 5x - 2\) (b) \(h (x) = -\dfrac{1}{3}x^2 + 3x\) (c) \(k (x) = 8x^2 - 5x - 7\) (d) \(j (x) = -\dfrac{71}{99}x^2 +210\) (e) \(f (x) = -4x^2 - 3x + 7\) (f) \(F (x) = -x^4 + x^3 + 9\)

Theorem If \(f\) is a quadratic function of the form \(f(x) = ax^2 + bx + c\) and ac < 0, then the function \(f\) has two x-intercepts.

Using only this theorem, what can be concluded about the functions given by the following formulas? (a) \(g (x) = -8x^2 + 5x - 2\) (b) \(h (x) = -\dfrac{1}{3}x^2 + 3x\) (c) \(k (x) = 8x^2 - 5x - 7\) (d) \(j (x) = -\dfrac{71}{99}x^2 +210\) (e) \(f (x) = -4x^2 - 3x + 7\) (f) \(F (x) = -x^4 + x^3 + 9\)

Theorem A. If \(f\) is a cubic function of the form \(f (x) = x^3 - x + b\) and b > 1, then the function \(f\) has exactly one \(x\)-intercept. Following is another theorem about \(x\)-intercepts of functions: Theorem B . If \(f\) and \(g\) are functions with \(g (x) = k \cdot f (x)\), where \(k\) is a nonzero real number, then \(f\) and \(g\) have exactly the same \(x\)-intercepts.

Using only these two theorems and some simple algebraic manipulations, what can be concluded about the functions given by the following formulas? (a) \(f (x) = x^3 -x + 7\) (b) \(g (x) = x^3 + x +7\) (c) \(h (x) = -x^3 + x - 5\) (d) \(k (x) = 2x^3 + 2x + 3\) (e) \(r (x) = x^4 - x + 11\) (f) \(F (x) = 2x^3 - 2x + 7\)

• (a) Is the set of natural numbers closed under division? (b) Is the set of rational numbers closed under division? (c) Is the set of nonzero rational numbers closed under division? (d) Is the set of positive rational numbers closed under division? (e) Is the set of positive real numbers closed under subtraction? (f) Is the set of negative rational numbers closed under division? (g) Is the set of negative integers closed under addition? Explorations and Activities
• Exploring Propositions . In Progress Check 1.2 , we used exploration to show that certain statements were false and to make conjectures that certain statements were true. We can also use exploration to formulate a conjecture that we believe to be true. For example, if we calculate successive powers of \(2, (2^1, 2^2, 2^3, 2^4, 2^5, ...)\) and examine the units digits of these numbers, we could make the following conjectures (among others): \(\bullet\) If \(n\) is a natural number, then the units digit of \(2^n\) must be 2, 4, 6, or 8. \(\bullet\) The units digits of the successive powers of 2 repeat according to the pattern “2, 4, 8, 6.” (a) Is it possible to formulate a conjecture about the units digits of successive powers of \(4 (4^1, 4^2, 4^3, 4^4, 4^5,...)\)? If so, formulate at least one conjecture. (b) Is it possible to formulate a conjecture about the units digit of numbers of the form \(7^n - 2^n\), where \(n\) is a natural number? If so, formulate a conjecture in the form of a conditional statement in the form “If \(n\) is a natural number, then ... .” (c) Let \(f (x) = e^(2x)\). Determine the first eight derivatives of this function. What do you observe? Formulate a conjecture that appears to be true. The conjecture should be written as a conditional statement in the form, “If n is a natural number, then ... .”

A hypothesis is a proposition that is consistent with known data, but has been neither verified nor shown to be false.

In statistics, a hypothesis (sometimes called a statistical hypothesis) refers to a statement on which hypothesis testing will be based. Particularly important statistical hypotheses include the null hypothesis and alternative hypothesis .

In symbolic logic , a hypothesis is the first part of an implication (with the second part being known as the predicate ).

In general mathematical usage, "hypothesis" is roughly synonymous with " conjecture ."

Explore with Wolfram|Alpha

More things to try:

• 30 choose 18
• Cesaro fractal

Cite this as:

Weisstein, Eric W. "Hypothesis." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/Hypothesis.html

Subject classifications

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Published 2008 Revised 2019

Understanding Hypotheses

'What happens if ... ?' to ' This will happen if'

The experimentation of children continually moves on to the exploration of new ideas and the refinement of their world view of previously understood situations. This description of the playtime patterns of young children very nicely models the concept of 'making and testing hypotheses'. It follows this pattern:

• Make some observations. Collect some data based on the observations.
• Draw a conclusion (called a 'hypothesis') which will explain the pattern of the observations.
• Test out your hypothesis by making some more targeted observations.

So, we have

• A hypothesis is a statement or idea which gives an explanation to a series of observations.

Sometimes, following observation, a hypothesis will clearly need to be refined or rejected. This happens if a single contradictory observation occurs. For example, suppose that a child is trying to understand the concept of a dog. He reads about several dogs in children's books and sees that they are always friendly and fun. He makes the natural hypothesis in his mind that dogs are friendly and fun . He then meets his first real dog: his neighbour's puppy who is great fun to play with. This reinforces his hypothesis. His cousin's dog is also very friendly and great fun. He meets some of his friends' dogs on various walks to playgroup. They are also friendly and fun. He is now confident that his hypothesis is sound. Suddenly, one day, he sees a dog, tries to stroke it and is bitten. This experience contradicts his hypothesis. He will need to amend the hypothesis. We see that

• Gathering more evidence/data can strengthen a hypothesis if it is in agreement with the hypothesis.
• If the data contradicts the hypothesis then the hypothesis must be rejected or amended to take into account the contradictory situation.

• A contradictory observation can cause us to know for certain that a hypothesis is incorrect.
• Accumulation of supporting experimental evidence will strengthen a hypothesis but will never let us know for certain that the hypothesis is true.

In short, it is possible to show that a hypothesis is false, but impossible to prove that it is true!

Whilst we can never prove a scientific hypothesis to be true, there will be a certain stage at which we decide that there is sufficient supporting experimental data for us to accept the hypothesis. The point at which we make the choice to accept a hypothesis depends on many factors. In practice, the key issues are

• What are the implications of mistakenly accepting a hypothesis which is false?
• What are the cost / time implications of gathering more data?
• What are the implications of not accepting in a timely fashion a true hypothesis?

For example, suppose that a drug company is testing a new cancer drug. They hypothesise that the drug is safe with no side effects. If they are mistaken in this belief and release the drug then the results could have a disastrous effect on public health. However, running extended clinical trials might be very costly and time consuming. Furthermore, a delay in accepting the hypothesis and releasing the drug might also have a negative effect on the health of many people.

In short, whilst we can never achieve absolute certainty with the testing of hypotheses, in order to make progress in science or industry decisions need to be made. There is a fine balance to be made between action and inaction.

Hypotheses and mathematics So where does mathematics enter into this picture? In many ways, both obvious and subtle:

• A good hypothesis needs to be clear, precisely stated and testable in some way. Creation of these clear hypotheses requires clear general mathematical thinking.
• The data from experiments must be carefully analysed in relation to the original hypothesis. This requires the data to be structured, operated upon, prepared and displayed in appropriate ways. The levels of this process can range from simple to exceedingly complex.

Very often, the situation under analysis will appear to be complicated and unclear. Part of the mathematics of the task will be to impose a clear structure on the problem. The clarity of thought required will actively be developed through more abstract mathematical study. Those without sufficient general mathematical skill will be unable to perform an appropriate logical analysis.

Using deductive reasoning in hypothesis testing

There is often confusion between the ideas surrounding proof, which is mathematics, and making and testing an experimental hypothesis, which is science. The difference is rather simple:

• Mathematics is based on deductive reasoning : a proof is a logical deduction from a set of clear inputs.
• Science is based on inductive reasoning : hypotheses are strengthened or rejected based on an accumulation of experimental evidence.

Of course, to be good at science, you need to be good at deductive reasoning, although experts at deductive reasoning need not be mathematicians. Detectives, such as Sherlock Holmes and Hercule Poirot, are such experts: they collect evidence from a crime scene and then draw logical conclusions from the evidence to support the hypothesis that, for example, Person M. committed the crime. They use this evidence to create sufficiently compelling deductions to support their hypotheses beyond reasonable doubt . The key word here is 'reasonable'. There is always the possibility of creating an exceedingly outlandish scenario to explain away any hypothesis of a detective or prosecution lawyer, but judges and juries in courts eventually make the decision that the probability of such eventualities are 'small' and the chance of the hypothesis being correct 'high'.

• If a set of data is normally distributed with mean 0 and standard deviation 0.5 then there is a 97.7% certainty that a measurement will not exceed 1.0.
• If the mean of a sample of data is 12, how confident can we be that the true mean of the population lies between 11 and 13?

It is at this point that making and testing hypotheses becomes a true branch of mathematics. This mathematics is difficult, but fascinating and highly relevant in the information-rich world of today.

To read more about the technical side of hypothesis testing, take a look at What is a Hypothesis Test?

You might also enjoy reading the articles on statistics on the Understanding Uncertainty website

This resource is part of the collection Statistics - Maths of Real Life

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.1: Introduction to Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 10211

• Kyle Siegrist
• University of Alabama in Huntsville via Random Services

Basic Theory

Preliminaries.

As usual, our starting point is a random experiment with an underlying sample space and a probability measure \(\P\). In the basic statistical model, we have an observable random variable \(\bs{X}\) taking values in a set \(S\). In general, \(\bs{X}\) can have quite a complicated structure. For example, if the experiment is to sample \(n\) objects from a population and record various measurements of interest, then \[ \bs{X} = (X_1, X_2, \ldots, X_n) \] where \(X_i\) is the vector of measurements for the \(i\)th object. The most important special case occurs when \((X_1, X_2, \ldots, X_n)\) are independent and identically distributed. In this case, we have a random sample of size \(n\) from the common distribution.

The purpose of this section is to define and discuss the basic concepts of statistical hypothesis testing . Collectively, these concepts are sometimes referred to as the Neyman-Pearson framework, in honor of Jerzy Neyman and Egon Pearson, who first formalized them.

A statistical hypothesis is a statement about the distribution of \(\bs{X}\). Equivalently, a statistical hypothesis specifies a set of possible distributions of \(\bs{X}\): the set of distributions for which the statement is true. A hypothesis that specifies a single distribution for \(\bs{X}\) is called simple ; a hypothesis that specifies more than one distribution for \(\bs{X}\) is called composite .

In hypothesis testing , the goal is to see if there is sufficient statistical evidence to reject a presumed null hypothesis in favor of a conjectured alternative hypothesis . The null hypothesis is usually denoted \(H_0\) while the alternative hypothesis is usually denoted \(H_1\).

An hypothesis test is a statistical decision ; the conclusion will either be to reject the null hypothesis in favor of the alternative, or to fail to reject the null hypothesis. The decision that we make must, of course, be based on the observed value \(\bs{x}\) of the data vector \(\bs{X}\). Thus, we will find an appropriate subset \(R\) of the sample space \(S\) and reject \(H_0\) if and only if \(\bs{x} \in R\). The set \(R\) is known as the rejection region or the critical region . Note the asymmetry between the null and alternative hypotheses. This asymmetry is due to the fact that we assume the null hypothesis, in a sense, and then see if there is sufficient evidence in \(\bs{x}\) to overturn this assumption in favor of the alternative.

An hypothesis test is a statistical analogy to proof by contradiction, in a sense. Suppose for a moment that \(H_1\) is a statement in a mathematical theory and that \(H_0\) is its negation. One way that we can prove \(H_1\) is to assume \(H_0\) and work our way logically to a contradiction. In an hypothesis test, we don't prove anything of course, but there are similarities. We assume \(H_0\) and then see if the data \(\bs{x}\) are sufficiently at odds with that assumption that we feel justified in rejecting \(H_0\) in favor of \(H_1\).

Often, the critical region is defined in terms of a statistic \(w(\bs{X})\), known as a test statistic , where \(w\) is a function from \(S\) into another set \(T\). We find an appropriate rejection region \(R_T \subseteq T\) and reject \(H_0\) when the observed value \(w(\bs{x}) \in R_T\). Thus, the rejection region in \(S\) is then \(R = w^{-1}(R_T) = \left\{\bs{x} \in S: w(\bs{x}) \in R_T\right\}\). As usual, the use of a statistic often allows significant data reduction when the dimension of the test statistic is much smaller than the dimension of the data vector.

The ultimate decision may be correct or may be in error. There are two types of errors, depending on which of the hypotheses is actually true.

Types of errors:

• A type 1 error is rejecting the null hypothesis \(H_0\) when \(H_0\) is true.
• A type 2 error is failing to reject the null hypothesis \(H_0\) when the alternative hypothesis \(H_1\) is true.

Similarly, there are two ways to make a correct decision: we could reject \(H_0\) when \(H_1\) is true or we could fail to reject \(H_0\) when \(H_0\) is true. The possibilities are summarized in the following table:

Of course, when we observe \(\bs{X} = \bs{x}\) and make our decision, either we will have made the correct decision or we will have committed an error, and usually we will never know which of these events has occurred. Prior to gathering the data, however, we can consider the probabilities of the various errors.

If \(H_0\) is true (that is, the distribution of \(\bs{X}\) is specified by \(H_0\)), then \(\P(\bs{X} \in R)\) is the probability of a type 1 error for this distribution. If \(H_0\) is composite, then \(H_0\) specifies a variety of different distributions for \(\bs{X}\) and thus there is a set of type 1 error probabilities.

The maximum probability of a type 1 error, over the set of distributions specified by \( H_0 \), is the significance level of the test or the size of the critical region.

The significance level is often denoted by \(\alpha\). Usually, the rejection region is constructed so that the significance level is a prescribed, small value (typically 0.1, 0.05, 0.01).

If \(H_1\) is true (that is, the distribution of \(\bs{X}\) is specified by \(H_1\)), then \(\P(\bs{X} \notin R)\) is the probability of a type 2 error for this distribution. Again, if \(H_1\) is composite then \(H_1\) specifies a variety of different distributions for \(\bs{X}\), and thus there will be a set of type 2 error probabilities. Generally, there is a tradeoff between the type 1 and type 2 error probabilities. If we reduce the probability of a type 1 error, by making the rejection region \(R\) smaller, we necessarily increase the probability of a type 2 error because the complementary region \(S \setminus R\) is larger.

The extreme cases can give us some insight. First consider the decision rule in which we never reject \(H_0\), regardless of the evidence \(\bs{x}\). This corresponds to the rejection region \(R = \emptyset\). A type 1 error is impossible, so the significance level is 0. On the other hand, the probability of a type 2 error is 1 for any distribution defined by \(H_1\). At the other extreme, consider the decision rule in which we always rejects \(H_0\) regardless of the evidence \(\bs{x}\). This corresponds to the rejection region \(R = S\). A type 2 error is impossible, but now the probability of a type 1 error is 1 for any distribution defined by \(H_0\). In between these two worthless tests are meaningful tests that take the evidence \(\bs{x}\) into account.

If \(H_1\) is true, so that the distribution of \(\bs{X}\) is specified by \(H_1\), then \(\P(\bs{X} \in R)\), the probability of rejecting \(H_0\) is the power of the test for that distribution.

Thus the power of the test for a distribution specified by \( H_1 \) is the probability of making the correct decision.

Suppose that we have two tests, corresponding to rejection regions \(R_1\) and \(R_2\), respectively, each having significance level \(\alpha\). The test with region \(R_1\) is uniformly more powerful than the test with region \(R_2\) if \[ \P(\bs{X} \in R_1) \ge \P(\bs{X} \in R_2) \text{ for every distribution of } \bs{X} \text{ specified by } H_1 \]

Naturally, in this case, we would prefer the first test. Often, however, two tests will not be uniformly ordered; one test will be more powerful for some distributions specified by \(H_1\) while the other test will be more powerful for other distributions specified by \(H_1\).

If a test has significance level \(\alpha\) and is uniformly more powerful than any other test with significance level \(\alpha\), then the test is said to be a uniformly most powerful test at level \(\alpha\).

Clearly a uniformly most powerful test is the best we can do.

\(P\)-value

In most cases, we have a general procedure that allows us to construct a test (that is, a rejection region \(R_\alpha\)) for any given significance level \(\alpha \in (0, 1)\). Typically, \(R_\alpha\) decreases (in the subset sense) as \(\alpha\) decreases.

The \(P\)-value of the observed value \(\bs{x}\) of \(\bs{X}\), denoted \(P(\bs{x})\), is defined to be the smallest \(\alpha\) for which \(\bs{x} \in R_\alpha\); that is, the smallest significance level for which \(H_0\) is rejected, given \(\bs{X} = \bs{x}\).

Knowing \(P(\bs{x})\) allows us to test \(H_0\) at any significance level for the given data \(\bs{x}\): If \(P(\bs{x}) \le \alpha\) then we would reject \(H_0\) at significance level \(\alpha\); if \(P(\bs{x}) \gt \alpha\) then we fail to reject \(H_0\) at significance level \(\alpha\). Note that \(P(\bs{X})\) is a statistic . Informally, \(P(\bs{x})\) can often be thought of as the probability of an outcome as or more extreme than the observed value \(\bs{x}\), where extreme is interpreted relative to the null hypothesis \(H_0\).

Analogy with Justice Systems

There is a helpful analogy between statistical hypothesis testing and the criminal justice system in the US and various other countries. Consider a person charged with a crime. The presumed null hypothesis is that the person is innocent of the crime; the conjectured alternative hypothesis is that the person is guilty of the crime. The test of the hypotheses is a trial with evidence presented by both sides playing the role of the data. After considering the evidence, the jury delivers the decision as either not guilty or guilty . Note that innocent is not a possible verdict of the jury, because it is not the point of the trial to prove the person innocent. Rather, the point of the trial is to see whether there is sufficient evidence to overturn the null hypothesis that the person is innocent in favor of the alternative hypothesis of that the person is guilty. A type 1 error is convicting a person who is innocent; a type 2 error is acquitting a person who is guilty. Generally, a type 1 error is considered the more serious of the two possible errors, so in an attempt to hold the chance of a type 1 error to a very low level, the standard for conviction in serious criminal cases is beyond a reasonable doubt .

Tests of an Unknown Parameter

Hypothesis testing is a very general concept, but an important special class occurs when the distribution of the data variable \(\bs{X}\) depends on a parameter \(\theta\) taking values in a parameter space \(\Theta\). The parameter may be vector-valued, so that \(\bs{\theta} = (\theta_1, \theta_2, \ldots, \theta_n)\) and \(\Theta \subseteq \R^k\) for some \(k \in \N_+\). The hypotheses generally take the form \[ H_0: \theta \in \Theta_0 \text{ versus } H_1: \theta \notin \Theta_0 \] where \(\Theta_0\) is a prescribed subset of the parameter space \(\Theta\). In this setting, the probabilities of making an error or a correct decision depend on the true value of \(\theta\). If \(R\) is the rejection region, then the power function \( Q \) is given by \[ Q(\theta) = \P_\theta(\bs{X} \in R), \quad \theta \in \Theta \] The power function gives a lot of information about the test.

The power function satisfies the following properties:

• \(Q(\theta)\) is the probability of a type 1 error when \(\theta \in \Theta_0\).
• \(\max\left\{Q(\theta): \theta \in \Theta_0\right\}\) is the significance level of the test.
• \(1 - Q(\theta)\) is the probability of a type 2 error when \(\theta \notin \Theta_0\).
• \(Q(\theta)\) is the power of the test when \(\theta \notin \Theta_0\).

If we have two tests, we can compare them by means of their power functions.

Suppose that we have two tests, corresponding to rejection regions \(R_1\) and \(R_2\), respectively, each having significance level \(\alpha\). The test with rejection region \(R_1\) is uniformly more powerful than the test with rejection region \(R_2\) if \( Q_1(\theta) \ge Q_2(\theta)\) for all \( \theta \notin \Theta_0 \).

Most hypothesis tests of an unknown real parameter \(\theta\) fall into three special cases:

Suppose that \( \theta \) is a real parameter and \( \theta_0 \in \Theta \) a specified value. The tests below are respectively the two-sided test , the left-tailed test , and the right-tailed test .

• \(H_0: \theta = \theta_0\) versus \(H_1: \theta \ne \theta_0\)
• \(H_0: \theta \ge \theta_0\) versus \(H_1: \theta \lt \theta_0\)
• \(H_0: \theta \le \theta_0\) versus \(H_1: \theta \gt \theta_0\)

Thus the tests are named after the conjectured alternative. Of course, there may be other unknown parameters besides \(\theta\) (known as nuisance parameters ).

Equivalence Between Hypothesis Test and Confidence Sets

There is an equivalence between hypothesis tests and confidence sets for a parameter \(\theta\).

Suppose that \(C(\bs{x})\) is a \(1 - \alpha\) level confidence set for \(\theta\). The following test has significance level \(\alpha\) for the hypothesis \( H_0: \theta = \theta_0 \) versus \( H_1: \theta \ne \theta_0 \): Reject \(H_0\) if and only if \(\theta_0 \notin C(\bs{x})\)

By definition, \(\P[\theta \in C(\bs{X})] = 1 - \alpha\). Hence if \(H_0\) is true so that \(\theta = \theta_0\), then the probability of a type 1 error is \(P[\theta \notin C(\bs{X})] = \alpha\).

Equivalently, we fail to reject \(H_0\) at significance level \(\alpha\) if and only if \(\theta_0\) is in the corresponding \(1 - \alpha\) level confidence set. In particular, this equivalence applies to interval estimates of a real parameter \(\theta\) and the common tests for \(\theta\) given above .

In each case below, the confidence interval has confidence level \(1 - \alpha\) and the test has significance level \(\alpha\).

• Suppose that \(\left[L(\bs{X}, U(\bs{X})\right]\) is a two-sided confidence interval for \(\theta\). Reject \(H_0: \theta = \theta_0\) versus \(H_1: \theta \ne \theta_0\) if and only if \(\theta_0 \lt L(\bs{X})\) or \(\theta_0 \gt U(\bs{X})\).
• Suppose that \(L(\bs{X})\) is a confidence lower bound for \(\theta\). Reject \(H_0: \theta \le \theta_0\) versus \(H_1: \theta \gt \theta_0\) if and only if \(\theta_0 \lt L(\bs{X})\).
• Suppose that \(U(\bs{X})\) is a confidence upper bound for \(\theta\). Reject \(H_0: \theta \ge \theta_0\) versus \(H_1: \theta \lt \theta_0\) if and only if \(\theta_0 \gt U(\bs{X})\).

Pivot Variables and Test Statistics

Recall that confidence sets of an unknown parameter \(\theta\) are often constructed through a pivot variable , that is, a random variable \(W(\bs{X}, \theta)\) that depends on the data vector \(\bs{X}\) and the parameter \(\theta\), but whose distribution does not depend on \(\theta\) and is known. In this case, a natural test statistic for the basic tests given above is \(W(\bs{X}, \theta_0)\).

Reset password New user? Sign up

Existing user? Log in

Hypothesis Testing

Already have an account? Log in here.

A hypothesis test is a statistical inference method used to test the significance of a proposed (hypothesized) relation between population statistics (parameters) and their corresponding sample estimators . In other words, hypothesis tests are used to determine if there is enough evidence in a sample to prove a hypothesis true for the entire population.

The test considers two hypotheses: the null hypothesis , which is a statement meant to be tested, usually something like "there is no effect" with the intention of proving this false, and the alternate hypothesis , which is the statement meant to stand after the test is performed. The two hypotheses must be mutually exclusive ; moreover, in most applications, the two are complementary (one being the negation of the other). The test works by comparing the \(p\)-value to the level of significance (a chosen target). If the \(p\)-value is less than or equal to the level of significance, then the null hypothesis is rejected.

When analyzing data, only samples of a certain size might be manageable as efficient computations. In some situations the error terms follow a continuous or infinite distribution, hence the use of samples to suggest accuracy of the chosen test statistics. The method of hypothesis testing gives an advantage over guessing what distribution or which parameters the data follows.

Definitions and Methodology

Hypothesis test and confidence intervals.

In statistical inference, properties (parameters) of a population are analyzed by sampling data sets. Given assumptions on the distribution, i.e. a statistical model of the data, certain hypotheses can be deduced from the known behavior of the model. These hypotheses must be tested against sampled data from the population.

The null hypothesis \((\)denoted \(H_0)\) is a statement that is assumed to be true. If the null hypothesis is rejected, then there is enough evidence (statistical significance) to accept the alternate hypothesis \((\)denoted \(H_1).\) Before doing any test for significance, both hypotheses must be clearly stated and non-conflictive, i.e. mutually exclusive, statements. Rejecting the null hypothesis, given that it is true, is called a type I error and it is denoted \(\alpha\), which is also its probability of occurrence. Failing to reject the null hypothesis, given that it is false, is called a type II error and it is denoted \(\beta\), which is also its probability of occurrence. Also, \(\alpha\) is known as the significance level , and \(1-\beta\) is known as the power of the test. \(H_0\) \(\textbf{is true}\)\(\hspace{15mm}\) \(H_0\) \(\textbf{is false}\) \(\textbf{Reject}\) \(H_0\)\(\hspace{10mm}\) Type I error Correct Decision \(\textbf{Reject}\) \(H_1\) Correct Decision Type II error The test statistic is the standardized value following the sampled data under the assumption that the null hypothesis is true, and a chosen particular test. These tests depend on the statistic to be studied and the assumed distribution it follows, e.g. the population mean following a normal distribution. The \(p\)-value is the probability of observing an extreme test statistic in the direction of the alternate hypothesis, given that the null hypothesis is true. The critical value is the value of the assumed distribution of the test statistic such that the probability of making a type I error is small.

Methodologies: Given an estimator \(\hat \theta\) of a population statistic \(\theta\), following a probability distribution \(P(T)\), computed from a sample \(\mathcal{S},\) and given a significance level \(\alpha\) and test statistic \(t^*,\) define \(H_0\) and \(H_1;\) compute the test statistic \(t^*.\) \(p\)-value Approach (most prevalent): Find the \(p\)-value using \(t^*\) (right-tailed). If the \(p\)-value is at most \(\alpha,\) reject \(H_0\). Otherwise, reject \(H_1\). Critical Value Approach: Find the critical value solving the equation \(P(T\geq t_\alpha)=\alpha\) (right-tailed). If \(t^*>t_\alpha\), reject \(H_0\). Otherwise, reject \(H_1\). Note: Failing to reject \(H_0\) only means inability to accept \(H_1\), and it does not mean to accept \(H_0\).

Assume a normally distributed population has recorded cholesterol levels with various statistics computed. From a sample of 100 subjects in the population, the sample mean was 214.12 mg/dL (milligrams per deciliter), with a sample standard deviation of 45.71 mg/dL. Perform a hypothesis test, with significance level 0.05, to test if there is enough evidence to conclude that the population mean is larger than 200 mg/dL. Hypothesis Test We will perform a hypothesis test using the \(p\)-value approach with significance level \(\alpha=0.05:\) Define \(H_0\): \(\mu=200\). Define \(H_1\): \(\mu>200\). Since our values are normally distributed, the test statistic is \(z^*=\frac{\bar X - \mu_0}{\frac{s}{\sqrt{n}}}=\frac{214.12 - 200}{\frac{45.71}{\sqrt{100}}}\approx 3.09\). Using a standard normal distribution, we find that our \(p\)-value is approximately \(0.001\). Since the \(p\)-value is at most \(\alpha=0.05,\) we reject \(H_0\). Therefore, we can conclude that the test shows sufficient evidence to support the claim that \(\mu\) is larger than \(200\) mg/dL.

If the sample size was smaller, the normal and \(t\)-distributions behave differently. Also, the question itself must be managed by a double-tail test instead.

Assume a population's cholesterol levels are recorded and various statistics are computed. From a sample of 25 subjects, the sample mean was 214.12 mg/dL (milligrams per deciliter), with a sample standard deviation of 45.71 mg/dL. Perform a hypothesis test, with significance level 0.05, to test if there is enough evidence to conclude that the population mean is not equal to 200 mg/dL. Hypothesis Test We will perform a hypothesis test using the \(p\)-value approach with significance level \(\alpha=0.05\) and the \(t\)-distribution with 24 degrees of freedom: Define \(H_0\): \(\mu=200\). Define \(H_1\): \(\mu\neq 200\). Using the \(t\)-distribution, the test statistic is \(t^*=\frac{\bar X - \mu_0}{\frac{s}{\sqrt{n}}}=\frac{214.12 - 200}{\frac{45.71}{\sqrt{25}}}\approx 1.54\). Using a \(t\)-distribution with 24 degrees of freedom, we find that our \(p\)-value is approximately \(2(0.068)=0.136\). We have multiplied by two since this is a two-tailed argument, i.e. the mean can be smaller than or larger than. Since the \(p\)-value is larger than \(\alpha=0.05,\) we fail to reject \(H_0\). Therefore, the test does not show sufficient evidence to support the claim that \(\mu\) is not equal to \(200\) mg/dL.

The complement of the rejection on a two-tailed hypothesis test (with significance level \(\alpha\)) for a population parameter \(\theta\) is equivalent to finding a confidence interval \((\)with confidence level \(1-\alpha)\) for the population parameter \(\theta\). If the assumption on the parameter \(\theta\) falls inside the confidence interval, then the test has failed to reject the null hypothesis \((\)with \(p\)-value greater than \(\alpha).\) Otherwise, if \(\theta\) does not fall in the confidence interval, then the null hypothesis is rejected in favor of the alternate \((\)with \(p\)-value at most \(\alpha).\)

• Statistics (Estimation)
• Normal Distribution
• Correlation
• Confidence Intervals

Problem Loading...

Note Loading...

Set Loading...

A statement that could be true, which might then be tested.

Example: Sam has a hypothesis that "large dogs are better at catching tennis balls than small dogs". We can test that hypothesis by having hundreds of different sized dogs try to catch tennis balls.

Sometimes the hypothesis won't be tested, it is simply a good explanation (which could be wrong). Conjecture is a better word for this.

Example: you notice the temperature drops just as the sun rises. Your hypothesis is that the sun warms the air high above you, which rises up and then cooler air comes from the sides.

Note: when someone says "I have a theory" they should say "I have a hypothesis", because in mathematics a theory is actually well proven.

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

5.2 - writing hypotheses.

The first step in conducting a hypothesis test is to write the hypothesis statements that are going to be tested. For each test you will have a null hypothesis (\(H_0\)) and an alternative hypothesis (\(H_a\)).

When writing hypotheses there are three things that we need to know: (1) the parameter that we are testing (2) the direction of the test (non-directional, right-tailed or left-tailed), and (3) the value of the hypothesized parameter.

• At this point we can write hypotheses for a single mean (\(\mu\)), paired means(\(\mu_d\)), a single proportion (\(p\)), the difference between two independent means (\(\mu_1-\mu_2\)), the difference between two proportions (\(p_1-p_2\)), a simple linear regression slope (\(\beta\)), and a correlation (\(\rho\)). 
• The research question will give us the information necessary to determine if the test is two-tailed (e.g., "different from," "not equal to"), right-tailed (e.g., "greater than," "more than"), or left-tailed (e.g., "less than," "fewer than").
• The research question will also give us the hypothesized parameter value. This is the number that goes in the hypothesis statements (i.e., \(\mu_0\) and \(p_0\)). For the difference between two groups, regression, and correlation, this value is typically 0.

Hypotheses are always written in terms of population parameters (e.g., \(p\) and \(\mu\)).  The tables below display all of the possible hypotheses for the parameters that we have learned thus far. Note that the null hypothesis always includes the equality (i.e., =).

Hypothesis Testing

Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.

A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.

What is Hypothesis Testing in Statistics?

Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.

Hypothesis Testing Definition

Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.

Null Hypothesis

The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as \(H_{0}\). Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.

Alternative Hypothesis

The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as \(H_{1}\) or \(H_{a}\). For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.

Hypothesis Testing P Value

In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, \(\alpha\) or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.

Hypothesis Testing Critical region

All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.

Hypothesis Testing Formula

Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:

• z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the size of the sample.
• t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). s is the sample standard deviation.
• \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\). \(O_{i}\) is the observed value and \(E_{i}\) is the expected value.

We will learn more about these test statistics in the upcoming section.

Types of Hypothesis Testing

Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.

Hypothesis Testing Z Test

A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:

• One sample: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
• Two samples: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing t Test

The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.

• One sample: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\).
• Two samples: t = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing Chi Square

The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.

One Tailed Hypothesis Testing

One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.

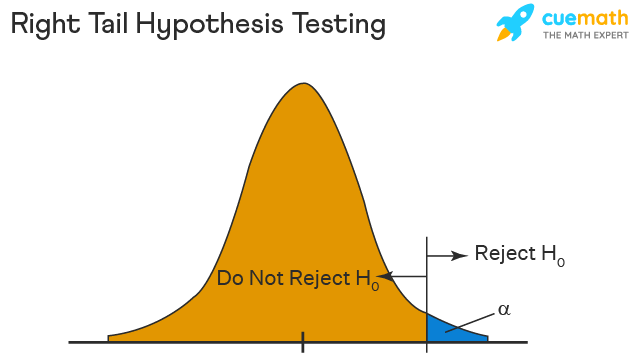
Right Tailed Hypothesis Testing

The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:

\(H_{0}\): The population parameter is ≤ some value

\(H_{1}\): The population parameter is > some value.

If the test statistic has a greater value than the critical value then the null hypothesis is rejected

Left Tailed Hypothesis Testing

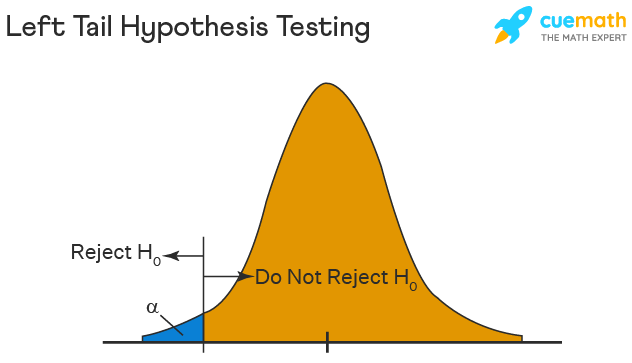
The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:

\(H_{0}\): The population parameter is ≥ some value

\(H_{1}\): The population parameter is < some value.

The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

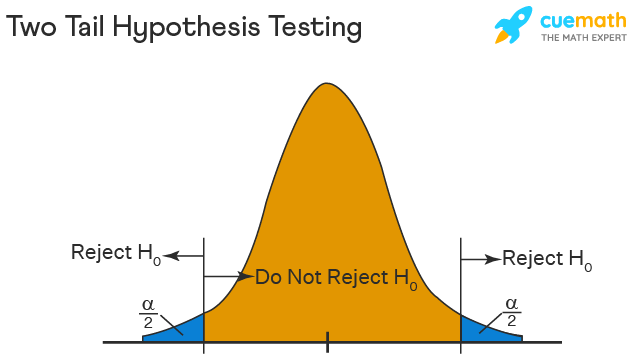
Two Tailed Hypothesis Testing

In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:

\(H_{0}\): the population parameter = some value

\(H_{1}\): the population parameter ≠ some value

The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

Hypothesis Testing Steps

Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:

• Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
• Step 2: Set up the alternative hypothesis.
• Step 3: Choose the correct significance level, \(\alpha\), and find the critical value.
• Step 4: Calculate the correct test statistic (z, t or \(\chi\)) and p-value.
• Step 5: Compare the test statistic with the critical value or compare the p-value with \(\alpha\) to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.

Hypothesis Testing Example

The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.

Step 1: This is an example of a right-tailed test. Set up the null hypothesis as \(H_{0}\): \(\mu\) = 100.

Step 2: The alternative hypothesis is given by \(H_{1}\): \(\mu\) > 100.

Step 3: As this is a one-tailed test, \(\alpha\) = 100% - 95% = 5%. This can be used to determine the critical value.

1 - \(\alpha\) = 1 - 0.05 = 0.95

0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.

Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).

\(\mu\) = 100, \(\overline{x}\) = 112.5, n = 30, \(\sigma\) = 15

z = \(\frac{112.5-100}{\frac{15}{\sqrt{30}}}\) = 4.56

Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.

Hypothesis Testing and Confidence Intervals

Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.

Related Articles:

• Probability and Statistics
• Data Handling

Important Notes on Hypothesis Testing

• Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
• It involves the setting up of a null hypothesis and an alternate hypothesis.
• There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
• Hypothesis testing can be classified as right tail, left tail, and two tail tests.

Examples on Hypothesis Testing

• Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) > 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 5, s = 18. \(\alpha\) = 0.05 Using the t-distribution table, the critical value is 2.132 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
• Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. \(H_{0}\): \(\mu\) = 80, \(H_{1}\): \(\mu\) ≠ 80 \(\overline{x}\) = 88, \(\mu\) = 80, n = 36, \(\sigma\) = 10. \(\alpha\) = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) z = \(\frac{88-80}{\frac{10}{\sqrt{36}}}\) = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
• Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) < 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = \(\frac{82-90}{\frac{18}{\sqrt{6}}}\) t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Hypothesis Testing

What is hypothesis testing.

Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.

What is the z Test in Hypothesis Testing?

The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.

What is the t Test in Hypothesis Testing?

The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?

The formula for a one sample z test in hypothesis testing is z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) and for two samples is z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

What is the p Value in Hypothesis Testing?

The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.

What is One Tail Hypothesis Testing?

When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.

What is the Alpha Level in Two Tail Hypothesis Testing?

To get the alpha level in a two tail hypothesis testing divide \(\alpha\) by 2. This is done as there are two rejection regions in the curve.

Conditional Statement – Definition, Truth Table, Examples, FAQs

What is a conditional statement, how to write a conditional statement, what is a biconditional statement, solved examples on conditional statements, practice problems on conditional statements, frequently asked questions about conditional statements.

A conditional statement is a statement that is written in the “If p, then q” format. Here, the statement p is called the hypothesis and q is called the conclusion. It is a fundamental concept in logic and mathematics. 

Conditional statement symbol :  p → q

A conditional statement consists of two parts.

• The “if” clause, which presents a condition or hypothesis.
• The “then” clause, which indicates the consequence or result that follows if the condition is true. 

Example : If you brush your teeth, then you won’t get cavities.

Hypothesis (Condition): If you brush your teeth

Conclusion (Consequence): then you won’t get cavities 

Conditional Statement: Definition

A conditional statement is characterized by the presence of “if” as an antecedent and “then” as a consequent. A conditional statement, also known as an “if-then” statement consists of two parts:

• The “if” clause (hypothesis): This part presents a condition, situation, or assertion. It is the initial condition that is being considered.
• The “then” clause (conclusion): This part indicates the consequence, result, or action that will occur if the condition presented in the “if” clause is true or satisfied. 

Related Worksheets

Representation of Conditional Statement

The conditional statement of the form ‘If p, then q” is represented as p → q. 

It is pronounced as “p implies q.”

Different ways to express a conditional statement are:

• p implies q
• p is sufficient for q
• q is necessary for p

Parts of a Conditional Statement

There are two parts of conditional statements, hypothesis and conclusion. The hypothesis or condition will begin with the “if” part, and the conclusion or action will begin with the “then” part. A conditional statement is also called “implication.”

Conditional Statements Examples:

Example 1: If it is Sunday, then you can go to play. 

Hypothesis: If it is Sunday

Conclusion: then you can go to play. 

Example 2: If you eat all vegetables, then you can have the dessert.

Condition: If you eat all vegetables

Conclusion: then you can have the dessert 

To form a conditional statement, follow these concise steps:

Step 1 : Identify the condition (antecedent or “if” part) and the consequence (consequent or “then” part) of the statement.

Step 2 : Use the “if… then…” structure to connect the condition and consequence.

Step 3 : Ensure the statement expresses a logical relationship where the condition leads to the consequence.

Example 1 : “If you study (condition), then you will pass the exam (consequence).” 

This conditional statement asserts that studying leads to passing the exam. If you study (condition is true), then you will pass the exam (consequence is also true).

Example 2 : If you arrange the numbers from smallest to largest, then you will have an ascending order.

Hypothesis: If you arrange the numbers from smallest to largest

Conclusion: then you will have an ascending order

Truth Table for Conditional Statement

The truth table for a conditional statement is a table used in logic to explore the relationship between the truth values of two statements. It lists all possible combinations of truth values for “p” and “q” and determines whether the conditional statement is true or false for each combination. 

The truth value of p → q is false only when p is true and q is False. 

If the condition is false, the consequence doesn’t affect the truth of the conditional; it’s always true.

In all the other cases, it is true.

The truth table is helpful in the analysis of possible combinations of truth values for hypothesis or condition and conclusion or action. It is useful to understand the presence of truth or false statements. 

Converse, Inverse, and Contrapositive

The converse, inverse, and contrapositive are three related conditional statements that are derived from an original conditional statement “p → q.” 

Consider a conditional statement: If I run, then I feel great.

• Converse: 

The converse of “p → q” is “q → p.” It reverses the order of the original statement. While the original statement says “if p, then q,” the converse says “if q, then p.” 

Converse: If I feel great, then I run.

• Inverse: 

The inverse of “p → q” is “~p → ~q,” where “” denotes negation (opposite). It negates both the antecedent (p) and the consequent (q). So, if the original statement says “if p, then q,” the inverse says “if not p, then not q.”

Inverse : If I don’t run, then I don’t feel great.

• Contrapositive: 

The contrapositive of “p → q” is “~q → ~p.” It reverses the order and also negates both the statements. So, if the original statement says “if p, then q,” the contrapositive says “if not q, then not p.”

Contrapositive: If I don’t feel great, then I don’t run.

A biconditional statement is a type of compound statement in logic that expresses a bidirectional or two-way relationship between two statements. It asserts that “p” is true if and only if “q” is true, and vice versa. In symbolic notation, a biconditional statement is represented as “p ⟺ q.”

In simpler terms, a biconditional statement means that the truth of “p” and “q” are interdependent. 

If “p” is true, then “q” must also be true, and if “q” is true, then “p” must be true. Conversely, if “p” is false, then “q” must be false, and if “q” is false, then “p” must be false. 

Biconditional statements are often used to express equality, equivalence, or conditions where two statements are mutually dependent for their truth values. 

Examples : 

• I will stop my bike if and only if the traffic light is red.  
• I will stay if and only if you play my favorite song.

Facts about Conditional Statements

• The negation of a conditional statement “p → q” is expressed as “p and not q.” It is denoted as “𝑝 ∧ ∼𝑞.” 
• The conditional statement is not logically equivalent to its converse and inverse.
• The conditional statement is logically equivalent to its contrapositive. 
• Thus, we can write p → q ∼q → ∼p

In this article, we learned about the fundamentals of conditional statements in mathematical logic, including their structure, parts, truth tables, conditional logic examples, and various related concepts. Understanding conditional statements is key to logical reasoning and problem-solving. Now, let’s solve a few examples and practice MCQs for better comprehension.

Example 1: Identify the hypothesis and conclusion. 

If you sing, then I will dance.

Solution : 

Given statement: If you sing, then I will dance.

Here, the antecedent or the hypothesis is “if you sing.”

The conclusion is “then I will dance.”

Example 2: State the converse of the statement: “If the switch is off, then the machine won’t work.” 

Here, p: The switch is off

q: The machine won’t work.

The conditional statement can be denoted as p → q.

Converse of p → q is written by reversing the order of p and q in the original statement.

Converse of  p → q is q → p.

Converse of  p → q: q → p: If the machine won’t work, then the switch is off.

Example 3: What is the truth value of the given conditional statement? 

If 2+2=5 , then pigs can fly.

Solution:  

q: Pigs can fly.

The statement p is false. Now regardless of the truth value of statement q, the overall statement will be true. 

F → F = T

Hence, the truth value of the statement is true. 

Conditional Statement - Definition, Truth Table, Examples, FAQs

Attend this quiz & Test your knowledge.

What is the antecedent in the given conditional statement? If it’s sunny, then I’ll go to the beach.

A conditional statement can be expressed as, what is the converse of “a → b”, when the antecedent is true and the consequent is false, the conditional statement is.

What is the meaning of conditional statements?

Conditional statements, also known as “if-then” statements, express a cause-and-effect or logical relationship between two propositions.

When does the truth value of a conditional statement is F?

A conditional statement is considered false when the antecedent is true and the consequent is false.

What is the contrapositive of a conditional statement?

The contrapositive reverses the order of the statements and also negates both the statements. It is equivalent in truth value to the original statement.

RELATED POSTS

• Ordering Decimals: Definition, Types, Examples
• Decimal to Octal: Steps, Methods, Conversion Table
• Lattice Multiplication – Definition, Method, Examples, Facts, FAQs
• X Intercept – Definition, Formula, Graph, Examples
• Lateral Face – Definition With Examples

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

Hypothesis test

A significance test, also referred to as a statistical hypothesis test, is a method of statistical inference in which observed data is compared to a claim (referred to as a hypothesis) in order to assess the truth of the claim. For example, one might wonder whether age affects the number of apples a person can eat, and may use a significance test to determine whether there is any evidence to suggest that it does.

Generally, the process of statistical hypothesis testing involves the following steps:

• State the null hypothesis.
• State the alternative hypothesis.
• Select the appropriate test statistic and select a significance level.
• Compute the observed value of the test statistic and its corresponding p-value.
• Reject the null hypothesis in favor of the alternative hypothesis, or do not reject the null hypothesis.

The null hypothesis

The null hypothesis, H 0 , is the claim that is being tested in a statistical hypothesis test. It typically is a statement that there is no difference between the populations being studied, or that there is no evidence to support a claim being made. For example, "age has no effect on the number of apples a person can eat."

A significance test is designed to test the evidence against the null hypothesis. This is because it is easier to prove that a claim is false than to prove that it is true; demonstrating that the claim is false in one case is sufficient, while proving that it is true requires that the claim be true in all cases.

The alternative hypothesis

The alternative hypothesis is the opposite of the null hypothesis in that it is a statement that there is some difference between the populations being studied. For example, "younger people can eat more apples than older people."

The alternative hypothesis is typically the hypothesis that researchers are trying to prove. A significance test is meant to determine whether there is sufficient evidence to reject the null hypothesis in favor of the alternative hypothesis. Note that the results of a significance test should either be to reject the null hypothesis in favor of the alternative hypothesis, or to not reject the null hypothesis. The result should not be to reject the alternative hypothesis or to accept the alternative hypothesis.

Test statistics and significance level

A test statistic is a statistic that is calculated as part of hypothesis testing that compares the distribution of observed data to the expected distribution, based on the null hypothesis. Examples of test statistics include the Z-score, T-statistic, F-statistic, and the Chi-square statistic. The test statistic used is dependent on the significance test used, which is dependent on the type of data collected and the type of relationship to be tested.

In many cases, the chosen significance level is 0.05, though 0.01 is also used. A significance level of 0.05 indicates that there is a 5% chance of rejecting the null hypothesis when the null hypothesis is actually true. Thus, a smaller selected significance level will require more evidence if the null hypothesis is to be rejected in favor of the alternative hypothesis.

After the test statistic is computed, the p-value can be determined based on the result of the test statistic. The p-value indicates the probability of obtaining test results that are at least as extreme as the observed results, under the assumption that the null hypothesis is correct. It tells us how likely it is to obtain a result based solely on chance. The smaller the p-value, the less likely a result can occur purely by chance, while a larger p-value makes it more likely. For example, a p-value of 0.01 means that there is a 1% chance that a result occurred solely by chance, given that the null hypothesis is true; a p-value of 0.90 means that there is a 90% chance.

A p-value is significantly affected by sample size. The larger the sample size, the smaller the p-value, even if the difference between populations may not be meaningful. On the other hand, if a sample size is too small, a meaningful difference may not be detected.

The last step in a significance test is to determine whether the p-value provides evidence that the null hypothesis should be rejected in favor of the alternative hypothesis. This is based on the selected significance level. If the p-value is less than or equal to the selected significance level, the null hypothesis is rejected in favor of the alternative hypothesis, and the result is deemed statistically significant. If the p-value is greater than the selected significance level, the null hypothesis is not rejected, and the result is deemed not statistically significant.

Discrete Mathematics: An Open Introduction, 3rd edition

Oscar Levin

Search Results:

Section 0.2 mathematical statements, investigate.

While walking through a fictional forest, you encounter three trolls guarding a bridge. Each is either a knight , who always tells the truth, or a knave , who always lies. The trolls will not let you pass until you correctly identify each as either a knight or a knave. Each troll makes a single statement:

Troll 1: If I am a knave, then there are exactly two knights here. Troll 2: Troll 1 is lying. Troll 3: Either we are all knaves or at least one of us is a knight.

Which troll is which?

In order to do mathematics, we must be able to talk and write about mathematics. Perhaps your experience with mathematics so far has mostly involved finding answers to problems. As we embark towards more advanced and abstract mathematics, writing will play a more prominent role in the mathematical process.

Communication in mathematics requires more precision than many other subjects, and thus we should take a few pages here to consider the basic building blocks: mathematical statements .

Subsection Atomic and Molecular Statements

A statement is any declarative sentence which is either true or false. A statement is atomic if it cannot be divided into smaller statements, otherwise it is called molecular .

Example 0.2.1 .

These are statements (in fact, atomic statements):

Telephone numbers in the USA have 10 digits.

The moon is made of cheese.

42 is a perfect square.

Every even number greater than 2 can be expressed as the sum of two primes.

\(\displaystyle 3+7 = 12\)

And these are not statements:

Would you like some cake?

The sum of two squares.

\(1+3+5+7+\cdots+2n+1\text{.}\)

Go to your room!

\(\displaystyle 3+x = 12\)

The reason the sentence “ \(3 + x = 12\) ” is not a statement is that it contains a variable. Depending on what \(x\) is, the sentence is either true or false, but right now it is neither. One way to make the sentence into a statement is to specify the value of the variable in some way. This could be done by specifying a specific substitution, for example, “ \(3+x = 12\) where \(x = 9\text{,}\) ” which is a true statement. Or you could capture the free variable by quantifying over it, as in, “for all values of \(x\text{,}\) \(3+x = 12\text{,}\) ” which is false. We will discuss quantifiers in more detail at the end of this section.

You can build more complicated (molecular) statements out of simpler (atomic or molecular) ones using logical connectives . For example, this is a molecular statement:

Telephone numbers in the USA have 10 digits and 42 is a perfect square.

Note that we can break this down into two smaller statements. The two shorter statements are connected by an “and.” We will consider 5 connectives: “and” (Sam is a man and Chris is a woman), “or” (Sam is a man or Chris is a woman), “if…, then…” (if Sam is a man, then Chris is a woman), “if and only if” (Sam is a man if and only if Chris is a woman), and “not” (Sam is not a man). The first four are called binary connectives (because they connect two statements) while “not” is an example of a unary connective (since it applies to a single statement).

These molecular statements are of course still statements, so they must be either true or false. The absolutely key observation here is that which truth value the molecular statement achieves is completely determined by the type of connective and the truth values of the parts. We do not need to know what the parts actually say, only whether those parts are true or false. So to analyze logical connectives, it is enough to consider propositional variables (sometimes called sentential variables), usually capital letters in the middle of the alphabet: \(P, Q, R, S, \ldots\text{.}\) We think of these as standing in for (usually atomic) statements, but there are only two values the variables can achieve: true or false.  1  We also have symbols for the logical connectives: \(\wedge\text{,}\) \(\vee\text{,}\) \(\imp\text{,}\) \(\iff\text{,}\) \(\neg\text{.}\)

Logical Connectives.

\(P \wedge Q\) is read “ \(P\) and \(Q\text{,}\) ” and called a conjunction .

\(P \vee Q\) is read “ \(P\) or \(Q\text{,}\) ” and called a disjunction .

\(P \imp Q\) is read “if \(P\) then \(Q\text{,}\) ” and called an implication or conditional .

\(P \iff Q\) is read “ \(P\) if and only if \(Q\text{,}\) ” and called a biconditional .

\(\neg P\) is read “not \(P\text{,}\) ” and called a negation .

The truth value of a statement is determined by the truth value(s) of its part(s), depending on the connectives:

Truth Conditions for Connectives.

\(P \wedge Q\) is true when both \(P\) and \(Q\) are true.

\(P \vee Q\) is true when \(P\) or \(Q\) or both are true.

\(P \imp Q\) is true when \(P\) is false or \(Q\) is true or both.

\(P \iff Q\) is true when \(P\) and \(Q\) are both true, or both false.

\(\neg P\) is true when \(P\) is false.

Note that for us, or is the inclusive or (and not the sometimes used exclusive or ) meaning that \(P \vee Q\) is in fact true when both \(P\) and \(Q\) are true. As for the other connectives, “and” behaves as you would expect, as does negation. The biconditional (if and only if) might seem a little strange, but you should think of this as saying the two parts of the statements are equivalent in that they have the same truth value. This leaves only the conditional \(P \imp Q\) which has a slightly different meaning in mathematics than it does in ordinary usage. However, implications are so common and useful in mathematics, that we must develop fluency with their use, and as such, they deserve their own subsection.

Subsection Implications

Implications..

An implication or conditional is a molecular statement of the form

where \(P\) and \(Q\) are statements. We say that

\(P\) is the hypothesis (or antecedent ).

\(Q\) is the conclusion (or consequent ).

An implication is true provided \(P\) is false or \(Q\) is true (or both), and false otherwise. In particular, the only way for \(P \imp Q\) to be false is for \(P\) to be true and \(Q\) to be false.

Easily the most common type of statement in mathematics is the implication. Even statements that do not at first look like they have this form conceal an implication at their heart. Consider the Pythagorean Theorem . Many a college freshman would quote this theorem as “ \(a^2 + b^2 = c^2\text{.}\) ” This is absolutely not correct. For one thing, that is not a statement since it has three variables in it. Perhaps they imply that this should be true for any values of the variables? So \(1^2 + 5^2 = 2^2\text{???}\) How can we fix this? Well, the equation is true as long as \(a\) and \(b\) are the legs of a right triangle and \(c\) is the hypotenuse. In other words:

If \(a\) and \(b\) are the legs of a right triangle with hypotenuse \(c\text{,}\) then \(a^2 + b^2 = c^2\text{.}\)

This is a reasonable way to think about implications: our claim is that the conclusion (“then” part) is true, but on the assumption that the hypothesis (“if” part) is true. We make no claim about the conclusion in situations when the hypothesis is false.  2 

Still, it is important to remember that an implication is a statement, and therefore is either true or false. The truth value of the implication is determined by the truth values of its two parts. To agree with the usage above, we say that an implication is true either when the hypothesis is false, or when the conclusion is true. This leaves only one way for an implication to be false: when the hypothesis is true and the conclusion is false.

Example 0.2.2 .

Consider the statement:

If Bob gets a 90 on the final, then Bob will pass the class.

This is definitely an implication: \(P\) is the statement “Bob gets a 90 on the final,” and \(Q\) is the statement “Bob will pass the class.”

Suppose I made that statement to Bob. In what circumstances would it be fair to call me a liar? What if Bob really did get a 90 on the final, and he did pass the class? Then I have not lied; my statement is true. However, if Bob did get a 90 on the final and did not pass the class, then I lied, making the statement false. The tricky case is this: what if Bob did not get a 90 on the final? Maybe he passes the class, maybe he doesn't. Did I lie in either case? I think not. In these last two cases, \(P\) was false, and the statement \(P \imp Q\) was true. In the first case, \(Q\) was true, and so was \(P \imp Q\text{.}\) So \(P \imp Q\) is true when either \(P\) is false or \(Q\) is true.

Just to be clear, although we sometimes read \(P \imp Q\) as “ \(P\) implies \(Q\) ”, we are not insisting that there is some causal relationship between the statements \(P\) and \(Q\text{.}\) In particular, if you claim that \(P \imp Q\) is false , you are not saying that \(P\) does not imply \(Q\text{,}\) but rather that \(P\) is true and \(Q\) is false.

Example 0.2.3 .

Decide which of the following statements are true and which are false. Briefly explain.

If \(1=1\text{,}\) then most horses have 4 legs.

If \(0=1\text{,}\) then \(1=1\text{.}\)

If 8 is a prime number, then the 7624th digit of \(\pi\) is an 8.

If the 7624th digit of \(\pi\) is an 8, then \(2+2 = 4\text{.}\)

All four of the statements are true. Remember, the only way for an implication to be false is for the if part to be true and the then part to be false.

Here both the hypothesis and the conclusion are true, so the implication is true. It does not matter that there is no meaningful connection between the true mathematical fact and the fact about horses.

Here the hypothesis is false and the conclusion is true, so the implication is true.

I have no idea what the 7624th digit of \(\pi\) is, but this does not matter. Since the hypothesis is false, the implication is automatically true.

Similarly here, regardless of the truth value of the hypothesis, the conclusion is true, making the implication true.

It is important to understand the conditions under which an implication is true not only to decide whether a mathematical statement is true, but in order to prove that it is. Proofs might seem scary (especially if you have had a bad high school geometry experience) but all we are really doing is explaining (very carefully) why a statement is true. If you understand the truth conditions for an implication, you already have the outline for a proof.

Direct Proofs of Implications.

To prove an implication \(P \imp Q\text{,}\) it is enough to assume \(P\text{,}\) and from it, deduce \(Q\text{.}\)

Perhaps a better way to say this is that to prove a statement of the form \(P \imp Q\) directly, you must explain why \(Q\) is true, but you get to assume \(P\) is true first. After all, you only care about whether \(Q\) is true in the case that \(P\) is as well.

There are other techniques to prove statements (implications and others) that we will encounter throughout our studies, and new proof techniques are discovered all the time. Direct proof is the easiest and most elegant style of proof and has the advantage that such a proof often does a great job of explaining why the statement is true.

Example 0.2.4 .

Prove: If two numbers \(a\) and \(b\) are even, then their sum \(a+b\) is even.

Suppose the numbers \(a\) and \(b\) are even. This means that \(a = 2k\) and \(b=2j\) for some integers \(k\) and \(j\text{.}\) The sum is then \(a+b = 2k+2j = 2(k+j)\text{.}\) Since \(k+j\) is an integer, this means that \(a+b\) is even.

Notice that since we get to assume the hypothesis of the implication, we immediately have a place to start. The proof proceeds essentially by repeatedly asking and answering, “what does that mean?” Eventually, we conclude that it means the conclusion.

This sort of argument shows up outside of math as well. If you ever found yourself starting an argument with “hypothetically, let's assume …,” then you have attempted a direct proof of your desired conclusion.

An implication is a way of expressing a relationship between two statements. It is often interesting to ask whether there are other relationships between the statements. Here we introduce some common language to address this question.

Converse and Contrapositive.

The converse of an implication \(P \imp Q\) is the implication \(Q \imp P\text{.}\) The converse is NOT logically equivalent to the original implication. That is, whether the converse of an implication is true is independent of the truth of the implication.

The contrapositive of an implication \(P \imp Q\) is the statement \(\neg Q \imp \neg P\text{.}\) An implication and its contrapositive are logically equivalent (they are either both true or both false).

Mathematics is overflowing with examples of true implications which have a false converse. If a number greater than 2 is prime, then that number is odd. However, just because a number is odd does not mean it is prime. If a shape is a square, then it is a rectangle. But it is false that if a shape is a rectangle, then it is a square.

However, sometimes the converse of a true statement is also true. For example, the Pythagorean theorem has a true converse: if \(a^2 + b^2 = c^2\text{,}\) then the triangle with sides \(a\text{,}\) \(b\text{,}\) and \(c\) is a right triangle. Whenever you encounter an implication in mathematics, it is always reasonable to ask whether the converse is true.

The contrapositive, on the other hand, always has the same truth value as its original implication. This can be very helpful in deciding whether an implication is true: often it is easier to analyze the contrapositive.

Example 0.2.5 .

True or false: If you draw any nine playing cards from a regular deck, then you will have at least three cards all of the same suit. Is the converse true?

True. The original implication is a little hard to analyze because there are so many different combinations of nine cards. But consider the contrapositive: If you don't have at least three cards all of the same suit, then you don't have nine cards. It is easy to see why this is true: you can at most have two cards of each of the four suits, for a total of eight cards (or fewer).

The converse: If you have at least three cards all of the same suit, then you have nine cards. This is false. You could have three spades and nothing else. Note that to demonstrate that the converse (an implication) is false, we provided an example where the hypothesis is true (you do have three cards of the same suit), but where the conclusion is false (you do not have nine cards).

Understanding converses and contrapositives can help understand implications and their truth values:

Example 0.2.6 .

Suppose I tell Sue that if she gets a 93% on her final, then she will get an A in the class. Assuming that what I said is true, what can you conclude in the following cases:

Sue gets a 93% on her final.

Sue gets an A in the class.

Sue does not get a 93% on her final.

Sue does not get an A in the class.

Note first that whenever \(P \imp Q\) and \(P\) are both true statements, \(Q\) must be true as well. For this problem, take \(P\) to mean “Sue gets a 93% on her final” and \(Q\) to mean “Sue will get an A in the class.”

We have \(P \imp Q\) and \(P\text{,}\) so \(Q\) follows. Sue gets an A.

You cannot conclude anything. Sue could have gotten the A because she did extra credit for example. Notice that we do not know that if Sue gets an \(A\text{,}\) then she gets a 93% on her final. That is the converse of the original implication, so it might or might not be true.

The contrapositive of the converse of \(P \imp Q\) is \(\neg P \imp \neg Q\text{,}\) which states that if Sue does not get a 93% on the final, then she will not get an A in the class. But this does not follow from the original implication. Again, we can conclude nothing. Sue could have done extra credit.

What would happen if Sue does not get an A but did get a 93% on the final? Then \(P\) would be true and \(Q\) would be false. This makes the implication \(P \imp Q\) false! It must be that Sue did not get a 93% on the final. Notice now we have the implication \(\neg Q \imp \neg P\) which is the contrapositive of \(P \imp Q\text{.}\) Since \(P \imp Q\) is assumed to be true, we know \(\neg Q \imp \neg P\) is true as well.

As we said above, an implication is not logically equivalent to its converse, but it is possible that both the implication and its converse are true. In this case, when both \(P \imp Q\) and \(Q \imp P\) are true, we say that \(P\) and \(Q\) are equivalent and write \(P \iff Q\text{.}\) This is the biconditional we mentioned earlier.

If and only if.

\(P \iff Q\) is logically equivalent to \((P \imp Q) \wedge (Q \imp P)\text{.}\)

Example: Given an integer \(n\text{,}\) it is true that \(n\) is even if and only if \(n^2\) is even. That is, if \(n\) is even, then \(n^2\) is even, as well as the converse: if \(n^2\) is even, then \(n\) is even.

You can think of “if and only if” statements as having two parts: an implication and its converse. We might say one is the “if” part, and the other is the “only if” part. We also sometimes say that “if and only if” statements have two directions: a forward direction \((P \imp Q)\) and a backwards direction ( \(P \leftarrow Q\text{,}\) which is really just sloppy notation for \(Q \imp P\) ).

Let's think a little about which part is which. Is \(P \imp Q\) the “if” part or the “only if” part? Consider an example.

Example 0.2.7 .

Suppose it is true that I sing if and only if I'm in the shower. We know this means both that if I sing, then I'm in the shower, and also the converse, that if I'm in the shower, then I sing. Let \(P\) be the statement, “I sing,” and \(Q\) be, “I'm in the shower.” So \(P \imp Q\) is the statement “if I sing, then I'm in the shower.” Which part of the if and only if statement is this?

What we are really asking for is the meaning of “I sing if I'm in the shower” and “I sing only if I'm in the shower.” When is the first one (the “if” part) false ? When I am in the shower but not singing. That is the same condition on being false as the statement “if I'm in the shower, then I sing.” So the “if” part is \(Q \imp P\text{.}\) On the other hand, to say, “I sing only if I'm in the shower” is equivalent to saying “if I sing, then I'm in the shower,” so the “only if” part is \(P \imp Q\text{.}\)

It is not terribly important to know which part is the “if” or “only if” part, but this does illustrate something very, very important: there are many ways to state an implication!

Example 0.2.8 .

Rephrase the implication, “if I dream, then I am asleep” in as many different ways as possible. Then do the same for the converse.

The following are all equivalent to the original implication:

I am asleep if I dream.

I dream only if I am asleep.

In order to dream, I must be asleep.

To dream, it is necessary that I am asleep.

To be asleep, it is sufficient to dream.

I am not dreaming unless I am asleep.

The following are equivalent to the converse (if I am asleep, then I dream):

I dream if I am asleep.

I am asleep only if I dream.

It is necessary that I dream in order to be asleep.

It is sufficient that I be asleep in order to dream.

If I don't dream, then I'm not asleep.

Hopefully you agree with the above example. We include the “necessary and sufficient” versions because those are common when discussing mathematics. In fact, let's agree once and for all what they mean.

Necessary and Sufficient.

“ \(P\) is necessary for \(Q\) ” means \(Q \imp P\text{.}\)

“ \(P\) is sufficient for \(Q\) ” means \(P \imp Q\text{.}\)

If \(P\) is necessary and sufficient for \(Q\text{,}\) then \(P \iff Q\text{.}\)

To be honest, I have trouble with these if I'm not very careful. I find it helps to keep a standard example for reference.

Example 0.2.9 .

Recall from calculus, if a function is differentiable at a point \(c\text{,}\) then it is continuous at \(c\text{,}\) but that the converse of this statement is not true (for example, \(f(x) = |x|\) at the point 0). Restate this fact using “necessary and sufficient” language.

It is true that in order for a function to be differentiable at a point \(c\text{,}\) it is necessary for the function to be continuous at \(c\text{.}\) However, it is not necessary that a function be differentiable at \(c\) for it to be continuous at \(c\text{.}\)

It is true that to be continuous at a point \(c\text{,}\) it is sufficient that the function be differentiable at \(c\text{.}\) However, it is not the case that being continuous at \(c\) is sufficient for a function to be differentiable at \(c\text{.}\)

Thinking about the necessity and sufficiency of conditions can also help when writing proofs and justifying conclusions. If you want to establish some mathematical fact, it is helpful to think what other facts would be enough (be sufficient) to prove your fact. If you have an assumption, think about what must also be necessary if that hypothesis is true.

Subsection Predicates and Quantifiers

Consider the statements below. Decide whether any are equivalent to each other, or whether any imply any others.

You can fool some people all of the time.

You can fool everyone some of the time.

You can always fool some people.

Sometimes you can fool everyone.

It would be nice to use variables in our mathematical sentences. For example, suppose we wanted to claim that if \(n\) is prime, then \(n+7\) is not prime. This looks like an implication. I would like to write something like

where \(P(n)\) means “ \(n\) is prime.” But this is not quite right. For one thing, because this sentence has a free variable (that is, a variable that we have not specified anything about), it is not a statement. A sentence that contains variables is called a predicate .

Now, if we plug in a specific value for \(n\text{,}\) we do get a statement. In fact, it turns out that no matter what value we plug in for \(n\text{,}\) we get a true implication in this case. What we really want to say is that for all values of \(n\text{,}\) if \(n\) is prime, then \(n+7\) is not. We need to quantify the variable.

Although there are many types of quantifiers in English (e.g., many, few, most, etc.) in mathematics we, for the most part, stick to two: existential and universal.

Universal and Existential Quantifiers.

The existential quantifier is \(\exists\) and is read “there exists” or “there is.” For example,

asserts that there is a number less than 0.

The universal quantifier is \(\forall\) and is read “for all” or “every.” For example,

asserts that every number is greater than or equal to 0.

As with all mathematical statements, we would like to decide whether quantified statements are true or false. Consider the statement

You would read this, “for every \(x\) there is some \(y\) such that \(y\) is less than \(x\text{.}\) ” Is this true? The answer depends on what our domain of discourse is: when we say “for all” \(x\text{,}\) do we mean all positive integers or all real numbers or all elements of some other set? Usually this information is implied. In discrete mathematics, we almost always quantify over the natural numbers , 0, 1, 2, …, so let's take that for our domain of discourse here.

For the statement to be true, we need it to be the case that no matter what natural number we select, there is always some natural number that is strictly smaller. Perhaps we could let \(y\) be \(x-1\text{?}\) But here is the problem: what if \(x = 0\text{?}\) Then \(y = -1\) and that is not a number! (in our domain of discourse). Thus we see that the statement is false because there is a number which is less than or equal to all other numbers. In symbols,

To show that the original statement is false, we proved that the negation was true. Notice how the negation and original statement compare. This is typical.

Quantifiers and Negation.

\(\neg \forall x P(x)\) is equivalent to \(\exists x \neg P(x)\text{.}\) \(\neg \exists x P(x)\) is equivalent to \(\forall x \neg P(x) \text{.}\)

Essentially, we can pass the negation symbol over a quantifier, but that causes the quantifier to switch type. This should not be surprising: if not everything has a property, then something doesn't have that property. And if there is not something with a property, then everything doesn't have that property.

Implicit Quantifiers.

It is always a good idea to be precise in mathematics. Sometimes though, we can relax a little bit, as long as we all agree on a convention. An example of such a convention is to assume that sentences containing predicates with free variables are intended as statements, where the variables are universally quantified.

For example, do you believe that if a shape is a square, then it is a rectangle? But how can that be true if it is not a statement? To be a little more precise, we have two predicates: \(S(x)\) standing for “ \(x\) is a square” and \(R(x)\) standing for “ \(x\) is a rectangle”. The sentence we are looking at is,

This is neither true nor false, as it is not a statement. But come on! We all know that we meant to consider the statement,

and this is what our convention tells us to consider.

Similarly, we will often be a bit sloppy about the distinction between a predicate and a statement. For example, we might write, let \(P(n)\) be the statement , “ \(n\) is prime,” which is technically incorrect. It is implicit that we mean that we are defining \(P(n)\) to be a predicate, which for each \(n\) becomes the statement, \(n\) is prime.

Exercises Exercises

For each sentence below, decide whether it is an atomic statement, a molecular statement, or not a statement at all.

atomic statement

molecular statement

not a statement

This is not a statement. It is an imperative sentence, but is not either true or false. It doesn’t matter that this might actually be the rule or not. Note that “The rule is that all customers must wear shoes” is a statement.

This is a statement, as it is either true or false. It is an atomic statement because it cannot be divided into smaller statements.

This is again a statement, but this time it is molecular. In fact, it is a conjunction, as we can write it as “The customers wore shoes and the customers wore socks.”

Classify each of the sentences below as an atomic statement, a molecular statement, or not a statement at all. If the statement is molecular, say what kind it is (conjunction, disjunction, conditional, biconditional, negation).

The sum of the first 100 odd positive integers.

Everybody needs somebody sometime.

The Broncos will win the Super Bowl or I'll eat my hat.

We can have donuts for dinner, but only if it rains.

Every natural number greater than 1 is either prime or composite.

This sentence is false.

Suppose \(P\) and \(Q\) are the statements: \(P\text{:}\) Jack passed math. \(Q\text{:}\) Jill passed math.

Translate “Jack and Jill both passed math” into symbols.

Translate “If Jack passed math, then Jill did not” into symbols.

Translate “ \(P \vee Q\) ” into English.

Translate “ \(\neg(P \wedge Q) \imp Q\) ” into English.

Suppose you know that if Jack passed math, then so did Jill. What can you conclude if you know that:

Jill passed math?

Jill did not pass math?

\(P \wedge Q\text{.}\)

\(P \imp \neg Q\text{.}\)

Jack passed math or Jill passed math (or both).

If Jack and Jill did not both pass math, then Jill did.

Nothing else.

Jack did not pass math either.

Determine whether each molecular statement below is true or false, or whether it is impossible to determine. Assume you do not know what my favorite number is (but you do know that 13 is prime).

Not enough information

It is impossible to tell. The hypothesis of the implication is true. Thus the implication will be true if the conclusion is true (if 13 is my favorite number) and false otherwise.

This is true, no matter whether 13 is my favorite number or not. Any implication with a true conclusion is true.

This is true, again, no matter whether 13 is my favorite number or not. Any implication with a false hypothesis is true.

For a disjunction to be true, we just need one or the other (or both) of the parts to be true. Thus this is a true statement.

We cannot tell. The statement would be true if 13 is my favorite number, and false if not (since a conjunction needs both parts to be true to be true).

This is definitely false. 13 is prime, so its negation (13 is not prime) is false. At least one part of the conjunction is false, so the whole statement is false.

This is true. Either 13 is my favorite number or it is not, but whichever it is, at least one part of the disjunction is true, so the whole statement is true.

In my safe is a sheet of paper with two shapes drawn on it in colored crayon. One is a square, and the other is a triangle. Each shape is drawn in a single color. Suppose you believe me when I tell you that if the square is blue, then the triangle is green . What do you therefore know about the truth value of the following statements?

The main thing to realize is that we don’t know the colors of these two shapes, but we do know that we are in one of three cases: We could have a blue square and green triangle. We could have a square that was not blue but a green triangle. Or we could have a square that was not blue and a triangle that was not green. The case in which the square is blue but the triangle is not green cannot occur, as that would make the statement false.

This must be false. In fact, this is the negation of the original implication.

This might be true or might be false.

True. This is the contrapositive of the original statement, which is logically equivalent to it.

We do not know. This is the converse of the original statement. In particular, if the square is not blue but the triangle is green, then the original statement is true but the converse is false.

True. This is logically equivalent to the original statement.

Again, suppose the statement “if the square is blue, then the triangle is green” is true. This time however, assume the converse is false. Classify each statement below as true or false (if possible).

The only way for an implication \(P\imp Q\) to be true but its converse to be false is for \(Q\) to be true and \(P\) to be false. Thus:

Consider the statement, “If you will give me a cow, then I will give you magic beans.” Decide whether each statement below is the converse, the contrapositive, or neither.

Contrapositive

The converse is “If I will give you magic beans, then you will give me a cow.” The contrapositive is “If I will not give you magic beans, then you will not give me a cow.” All the other statements are neither the converse nor contrapositive.

Consider the statement “If Oscar eats Chinese food, then he drinks milk.”

Write the converse of the statement.

Write the contrapositive of the statement.

Is it possible for the contrapositive to be false? If it was, what would that tell you?

Suppose the original statement is true, and that Oscar drinks milk. Can you conclude anything (about his eating Chinese food)? Explain.

Suppose the original statement is true, and that Oscar does not drink milk. Can you conclude anything (about his eating Chinese food)? Explain.

You have discovered an old paper on graph theory that discusses the viscosity of a graph (which for all you know, is something completely made up by the author). A theorem in the paper claims that “if a graph satisfies condition (V) , then the graph is viscous .” Which of the following are equivalent ways of stating this claim? Which are equivalent to the converse of the claim?

Equivalent to the converse.

Equivalent to the original theorem.

Write each of the following statements in the form, “if …, then ….” Careful, some of the statements might be false (which is alright for the purposes of this question).

To lose weight, you must exercise.

To lose weight, all you need to do is exercise.

Every American is patriotic.

You are patriotic only if you are American.

The set of rational numbers is a subset of the real numbers.

A number is prime if it is not even.

Either the Broncos will win the Super Bowl, or they won't play in the Super Bowl.

If you have lost weight, then you exercised.

If you exercise, then you will lose weight.

If you are American, then you are patriotic.

If you are patriotic, then you are American.

If a number is rational, then it is real.

If a number is not even, then it is prime. (Or the contrapositive: if a number is not prime, then it is even.)

If the Broncos don't win the Super Bowl, then they didn't play in the Super Bowl. Alternatively, if the Broncos play in the Super Bowl, then they will win the Super Bowl.

Which of the following statements are equivalent to the implication, “if you win the lottery, then you will be rich,” and which are equivalent to the converse of the implication?

Either you win the lottery or else you are not rich.

Either you don't win the lottery or else you are rich.

You will win the lottery and be rich.

You will be rich if you win the lottery.

You will win the lottery if you are rich.

It is necessary for you to win the lottery to be rich.

It is sufficient to win the lottery to be rich.

You will be rich only if you win the lottery.

Unless you win the lottery, you won't be rich.

If you are rich, you must have won the lottery.

If you are not rich, then you did not win the lottery.

You will win the lottery if and only if you are rich.

Let \(P(x)\) be the predicate, “ \(3x+1\) is even.”

Neither (not a statement)

What, if anything, can you conclude about \(\exists x P(x)\) from the truth value of \(P(5)\text{?}\)

What, if anything, can you conclude about \(\forall x P(x)\) from the truth value of \(P(5)\text{?}\)

\(P(5)\) is the statement “ \(3\cdot 5 + 1\) is even”, which is true. Thus the statement \(\exists x P(x)\) is true (for example, 5 is such an \(x\) ). However, we cannot tell anything about \(\forall x P(x)\) since we do not know the truth value of \(P(x)\) for all elements of the domain of discourse. In this case, \(\forall x P(x)\) happens to be false (since \(P(4)\) is false, for example).

Let \(P(x)\) be the predicate, “ \(4x+1\) is even.”

For a given predicate \(P(x)\text{,}\) you might believe that the statements \(\forall x P(x)\) or \(\exists x P(x)\) are either true or false. How would you decide if you were correct in each case? You have four choices: you could give an example of an element \(n\) in the domain for which \(P(n)\) is true or for which \(P(n)\) if false, or you could argue that no matter what \(n\) is, \(P(n)\) is true or is false.

What would you need to do to prove \(\forall x P(x)\) is true?

What would you need to do to prove \(\forall x P(x)\) is false?

What would you need to do to prove \(\exists x P(x)\) is true?

What would you need to do to prove \(\exists x P(x)\) is false?

The claim that \(\forall x P(x)\) means that \(P(n)\) is true no matter what \(n\) you consider in the domain of discourse. Thus the only way to prove that \(\forall x P(x)\) is true is to check or otherwise argue that \(P(n)\) is true for all \(n\) in the domain.

To prove \(\forall x P(x)\) is false all you need is one example of an element in the domain for which \(P(n)\) is false. This is often called a counterexample.

We are simply claiming that there is some element \(n\) in the domain of discourse for which \(P(n)\) is true. If you can find one such element, you have verified the claim.

Here we are claiming that no element we find will make \(P(n)\) true. The only way to be sure of this is to verify that every element of the domain makes \(P(n)\) false. Note that the level of proof needed for this statement is the same as to prove that \(\forall x P(x)\) is true.

Suppose \(P(x,y)\) is some binary predicate defined on a very small domain of discourse: just the integers 1, 2, 3, and 4. For each of the 16 pairs of these numbers, \(P(x,y)\) is either true or false, according to the following table ( \(x\) values are rows, \(y\) values are columns).

For example, \(P(1,3)\) is false, as indicated by the F in the first row, third column.

Use the table to decide whether the following statements are true or false.

\(\forall x \exists y P(x,y)\) is false because when \(x = 4\text{,}\) there is no \(y\) which makes \(P(4,y)\) true.

\(\forall y \exists x P(x,y)\) is true. No matter what \(y\) is (i.e., no matter what column we are in) there is some \(x\) for which \(P(x,y)\) is true. In fact, we can always take \(x\) to be \(3\text{.}\)

\(\exists x \forall y P(x,y)\) is true. In particular \(x=3\) is such a number, so that no matter what \(y\) is, \(P(x,y)\) is true.

\(\exists y \forall x P(x,y)\) is false. In fact, no matter what \(y\) (column) we look at, there is always some \(x\) (row) which makes \(P(x,y)\) false.

Translate into symbols. Use \(E(x)\) for “ \(x\) is even” and \(O(x)\) for “ \(x\) is odd.”

No number is both even and odd.

One more than any even number is an odd number.

There is prime number that is even.

Between any two numbers there is a third number.

There is no number between a number and one more than that number.

\(\neg \exists x (E(x) \wedge O(x))\text{.}\)

\(\forall x (E(x) \imp O(x+1))\text{.}\)

\(\exists x(P(x) \wedge E(x))\) (where \(P(x)\) means “ \(x\) is prime”).

\(\forall x \forall y \exists z(x \lt z \lt y \vee y \lt z \lt x)\text{.}\)

\(\forall x \neg \exists y (x \lt y \lt x+1)\text{.}\)

Translate into English:

\(\forall x (E(x) \imp E(x +2))\text{.}\)

\(\forall x \exists y (\sin(x) = y)\text{.}\)

\(\forall y \exists x (\sin(x) = y)\text{.}\)

\(\forall x \forall y (x^3 = y^3 \imp x = y)\text{.}\)

Any even number plus 2 is an even number.

For any \(x\) there is a \(y\) such that \(\sin(x) = y\text{.}\) In other words, every number \(x\) is in the domain of sine.

For every \(y\) there is an \(x\) such that \(\sin(x) = y\text{.}\) In other words, every number \(y\) is in the range of sine (which is false).

For any numbers, if the cubes of two numbers are equal, then the numbers are equal.

Suppose \(P(x)\) is some predicate for which the statement \(\forall x P(x)\) is true. Is it also the case that \(\exists x P(x)\) is true? In other words, is the statement \(\forall x P(x) \imp \exists x P(x)\) always true? Is the converse always true? Assume the domain of discourse is non-empty.

Try an example. What if \(P(x)\) was the predicate, “ \(x\) is prime”? What if it was “if \(x\) is divisible by 4, then it is even”? Of course examples are not enough to prove something in general, but that is entirely the point of this question.

For each of the statements below, give a domain of discourse for which the statement is true, and a domain for which the statement is false.

\(\forall x \exists y (y^2 = x)\text{.}\)

\(\forall x \forall y (x \lt y \imp \exists z (x \lt z \lt y))\text{.}\)

\(\exists x \forall y \forall z (y \lt z \imp y \le x \le z)\text{.}\)

First figure out what each statement is saying. For part (c), you don't need to assume the domain is an infinite set.

Consider the statement, “For all natural numbers \(n\text{,}\) if \(n\) is prime, then \(n\) is solitary.” You do not need to know what solitary means for this problem, just that it is a property that some numbers have and others do not.

Write the converse and the contrapositive of the statement, saying which is which. Note: the original statement claims that an implication is true for all \(n\text{,}\) and it is that implication that we are taking the converse and contrapositive of.

Write the negation of the original statement. What would you need to show to prove that the statement is false?

Even though you don't know whether 10 is solitary (in fact, nobody knows this), is the statement “if 10 is prime, then 10 is solitary” true or false? Explain.

It turns out that 8 is solitary. Does this tell you anything about the truth or falsity of the original statement, its converse or its contrapositive? Explain.

Assuming that the original statement is true, what can you say about the relationship between the set \(P\) of prime numbers and the set \(S\) of solitary numbers. Explain.

• Search Menu
• Advance articles
• Author Guidelines
• Submission Site
• Open Access
• About International Mathematics Research Notices
• Editorial Board
• Advertising and Corporate Services
• Journals Career Network
• Self-Archiving Policy
• Dispatch Dates
• Journals on Oxford Academic
• Books on Oxford Academic

Article Contents

1 introduction, 2 some preliminaries, 3 the main theorem, 4 final remarks, a algebras in equivariant cartesian symmetric monoidal structures, acknowledgments.

• < Previous

An Equivariant Generalisation of McDuff–Segal’s Group–Completion Theorem

• Article contents
• Figures & tables
• Supplementary Data

Kaif Hilman, An Equivariant Generalisation of McDuff–Segal’s Group–Completion Theorem, International Mathematics Research Notices , Volume 2024, Issue 9, May 2024, Pages 7552–7570, https://doi.org/10.1093/imrn/rnad278

• Permissions Icon Permissions

In this short note, we prove a |$G$| –equivariant generalisation of McDuff–Segal’s group–completion theorem for finite groups |$G$|⁠ . A new complication regarding genuine equivariant localisations arises and we resolve this by isolating a simple condition on the homotopy groups of |$\mathbb{E}_{\infty }$| –rings in |$G$| –spectra. We check that this condition is satisfied when our inputs are a suitable variant of |$\mathbb{E}_{\infty }$| –monoids in |$G$| –spaces via the existence of multiplicative norm structures, thus giving a localisation formula for their associated |$G$| –spherical group rings.

Group–completion is an important procedure in higher algebra for at least two reasons: (1) it is the main ingredient in constructing the K–theory of symmetric monoidal ( ⁠|$\infty -$|⁠ )categories; (2) it allows one to port spectral methods to study questions regarding moduli spaces. The homotopy types of these group–completions are however mysterious in general, and the group–completion theorem of McDuff–Segal [ 19 , 24 ] is a classical tool giving a homological formula for these objects. By now, the theorem has become a standard component, for example, in the active area burgeoning in the wake of the Madsen–Weiss theorem (cf. [ 8 , §7.4] and [ 9 , §7]) relating the homology of diffeomorphism groups to something amenable to stable homotopy theoretic methods. Very roughly speaking, the strategy is first to show that the group–completion of a geometrically defined cobordism category associated to the diffeomorphism groups is equivalent to a particular Thom spectrum. One then combines this identification with the group–completion theorem to compute, up to stabilisation, the homology of the said diffeomorphism groups in terms of the homology of the Thom spectrum.

In this article, we investigate a |$G$| –equivariant generalisation of this classical result for finite groups |$G$|⁠ . This is not as contrived a question as it may first seem since one of the main steps for an equivariant generalisation of the “Madsen–Weiss program” above has already been explored in [ 10 , Thm. 1.1] where they identified the group–completion of a certain equivariant cobordism category with an equivariant Madsen–Tillmann spectrum. Our hope is that the result we present here could provide one of the standard pieces in a future equivariant story and serve as a useful tool for making Bredon homological analyses of equivariant group–completions.

In this paper, by a category, we will always mean an |$\infty $| –category in the sense of [ 17 ]. When emphasising that something is a category in the classical sense, we will term it as a 1–category .

We will briefly introduce some notions so as to be able to state the main theorem. More details on all these can be found in § 2 . We write |${\mathcal{O}}_{G}$| for the orbit category of the finite group |$G$| and |${\mathcal{S}}_{G}:= \textrm{Fun}({\mathcal{O}}_{G}^{\textrm{op}},{\mathcal{S}})$| for the category of genuine |$G$| –spaces , and write |$\textrm{CMon}({\mathcal{S}}_{G})\simeq \textrm{Fun}({\mathcal{O}}_{G}^{\textrm{op}},\textrm{CMon}({\mathcal{S}}))$| for the category of |$\mathbb{E}_{\infty }$| –monoid objects therein. An object |$M\in \textrm{CMon}({\mathcal{S}}_{G})$| consists of |$\mathbb{E}_{\infty }$| –monoid spaces |$M^{H}$| for every subgroup |$H\leq G$| and the restriction map |$M^{H}\rightarrow M^{K}$| associated to a subconjugation |$K\leq H$| is a map of |$\mathbb{E}_{\infty }$| –monoids.

There is a variant with more equivariant structure, namely the category |$\textrm{CMon}_{G}(\underline{{\mathcal{S}}}_{G})$| of |$G$| – |$\mathbb{E}_{\infty }$| –monoids in genuine |$G$| –spaces . An object |$M\in \textrm{CMon}_{G}(\underline{{\mathcal{S}}}_{G})$| consists of the data above together with “equivariant addition” maps |$\oplus _{H/K} \colon M^{K}\rightarrow M^{H}$| for every |$K\leq H$| satisfying double–coset formulas and higher coherences. This turns out, as we shall recall at the end of Construction 2.6 , to be equivalent to the category |$\textrm{Mack}_{G}({\mathcal{S}}):= \textrm{Fun}^{\times }(A^{\textrm{eff}}(G),{\mathcal{S}})$| of |$G$| –Mackey functors valued in spaces defined as product–preserving presheaves on Barwick’s effective Burnside category (cf. [ 7 , Rmk. 2.3]). There is a forgetful functor |$\textrm{fgt} \colon \textrm{CMon}_{G}(\underline{{\mathcal{S}}}_{G}) \rightarrow \textrm{CMon}({\mathcal{S}}_{G})$| forgetting the equivariant addition maps.

While we reserve the more general—but notationally heavier—statement of the main result Theorem 3.3 in the body of the paper, we can however extract the following simple consequence on Bredon homology here (whose proof is given at the end of § 3 after the proof of Theorem 3.3 ):

  Theorem 1.3. Let |$M\in \textrm{CMon}_{G}(\underline{{\mathcal{S}}}_{G})$| and |$\underline{N}$| a |$G$| –Mackey functor valued in abelian groups. For any |$K\leq G$|⁠ , we have a natural isomorphism of |$RO(K)$| –graded Bredon homology with |$\underline{N}$| coefficients $$\begin{align*} &H_{\star}^{K}(\Omega BM; \underline{N}) \cong H_{\star}^{K}(M; \underline{N})[(\pi_{0}M^{K})^{-1}].\end{align*}$$

The reader might now justifiably wonder how common |$G$| – |$\mathbb{E}_{\infty }$| –monoid |$G$| –spaces actually are. To address this point somewhat, we will recall a standard mechanism to produce plenty of interesting examples in Example 4.5 .

We now look ahead slightly to say a few words about what is actually proved in Theorem 3.3 and the methods involved. The general formulation is in terms of higher algebraic localisations of spherical monoid rings (following that of Nikolaus [ 23 ]) and the result will be in two parts: in part (i), we show using a direct adaptation of the proof in [ 23 , Thm. 1] that for |$M\in \textrm{CMon}({\mathcal{S}}_{G})$|⁠ , the |$G$| –suspension spectrum of its group completion is computed as an abstract localisation satisfying a universal property. The crux of the matter here is that, unlike the nonequivariant case where one can prove that the abstract localisation can always be identified with a telescopic localisation as appears in Theorem 1.3 (cf. e.g., [ 23 , App. A] for the proof of this in the general case of |$\mathbb{E}_{1}$| –rings satisfying the Ore condition), this is not so in the equivariant setting. However, we do show in part (ii) of Theorem 3.3 that when |$M$| has the additional structure of a |$G$| – |$\mathbb{E}_{\infty }$| –monoid |$G$| –space, the associated |$G$| –spherical monoid ring attains the structure of the multiplicative norms (in the sense of [ 12 , 15 ]), which in turn ensures that the abstract and telescopic localisations agree. In fact, we will isolate a simple condition on the equivariant homotopy groups of |$M$| we call torsion–extension (cf. Condition 3.4 ), which ensures that the abstract and telescopic localisations agree even in the absence of the norms. This might be usable and useful in specific cases of |$M$|⁠ .

As far as we know, the theorem cannot be directly deduced from the classical group–completion theorem because the |$G$| –suspension spectrum of a |$G$| –space is not given simply by taking the suspension spectrum on each genuine fixed points of the |$G$| –space. The first part of the theorem will require only standard |$\infty $| –category theory (essentially the same proof as [ 23 , Thm. 1] as pointed out above), whereas in the more highly structured second part of Theorem 3.3 we will need the language of |$G$| –categories introduced in [ 1 ] in order to discuss |$G$| – |$\mathbb{E}_{\infty }$| structures succinctly. To our untrained eyes, the relevance of the multiplicative norms came as a bit of a surprise, but in hindsight, this result is likely known or at least expected among experts. While we were not able to find this result in the literature, we very much welcome a reference to where this result might have previously appeared and give the appropriate credits.

Lastly, a few words on organisation: we will briefly record some foundational materials in § 2 to orient the reader who might not be familiar with the formalism of |$G$| –categories; in § 3 , we give a proof of the main Theorem 3.3 ; and in § 4 we will end the main body of the article with some remarks on how norms and localisations managed to interplay well in our situation and how this result fits in with the nonequivariant group–completion theorem. Along the way, we will explain how geometric fixed points turn the mysterious localisation |$L_{\underline{S}^{-1}}R$| into something familiar. We also record a generic situation where this theorem might be useful and give a rich source of examples of |$G$| – |$\mathbb{E}_{\infty }$| –monoid |$G$| –spaces. Finally, in Appendix   A , we will prove a technical folklore result, which we use in proving the main theorem, namely that |$G$| – |$\mathbb{E}_{\infty }$| algebras in |$G$| –cartesian symmetric monoidal |$G$| –categories are the same as |$G$| – |$\mathbb{E}_{\infty }$| –monoids in said |$G$| –category. We have unfortunately not been able to find this in the literature and hope that this appendix will serve to fill in this gap.

Let |$G$| be a finite group.

Let |${\mathcal{O}}_{G}$| be the orbit category of the finite group |$G$|⁠ : this is a 1–category whose objects are transitive |$G$| –sets and morphisms are |$G$| –equivariant maps. We write |${\mathcal{S}}_{G}$| for the category of genuine |$G$| –spaces, which is defined to be |${\mathcal{S}}_{G}:= \textrm{Fun}({\mathcal{O}}_{G}^{\textrm{op}},{\mathcal{S}})$| where |${\mathcal{S}}$| is the category of spaces, and we write |$\textrm{Sp}_{G}$| for the category of genuine |$G$| –spectra, a model of which is given by |$G$| –Mackey functors valued in spectra (cf. [ 2 , 3 ]). We will also denote by |${\mathbb{S}}_{G}[-]$| for the functor |${\Sigma }^{\infty }_{+G}\colon{\mathcal{S}}_{G}\rightarrow \textrm{Sp}_{G}$| given by taking the |$G$| –suspension spectrum.

For a category |${\mathcal{C}}$| admitting finite products, we write |$\textrm{CMon}({\mathcal{C}})$| for the category of |$\mathbb{E}_{\infty }$| –monoids in |${\mathcal{C}}$|⁠ ; for a symmetric monoidal category |${\mathcal{D}}^{\otimes }$|⁠ , we write |$\textrm{CAlg}({\mathcal{D}}^{\otimes })$| for the |$\mathbb{E}_{\infty }$| –algebra objects in |${\mathcal{D}}$| under the endowed tensor product structure. Writing |${\mathcal{C}}^{\times }$| for the cartesian symmetric monoidal structure, we then have by [ 17 , Prop. 2.4.2.5] that |$\textrm{CAlg}({\mathcal{C}}^{\times })\simeq \textrm{CMon}({\mathcal{C}})$|⁠ . Note that this means |$\textrm{CAlg}(\textrm{Sp}_{G}^{\otimes })$| denotes |$\mathbb{E}_{\infty }$| –rings in genuine |$G$| –spectra without the multiplicative norms.

We begin with the following observation, which requires no theory of |$G$| –categories:

Now, to set the stage for our discussions about the multiplicative norms, we collect here some basics on |$G$| –categories. The reader uninterested in this refinement can skip right away to the proof of the first part of Theorem 3.3 in the next section.

In keeping with the tradition of papers about group–completions, we aim to keep this article as compact as possible. As such, we have chosen to travel light in this document and we refrain from giving a self–contained exposition of the required theory on |$G$| –categories. For the original sources of these materials, we refer the reader to [ 1 , 20 , 27 ], and a one–stop survey of |$G$| –categories can be found for example in [ 16 , Chap. 1]. In short, a |$G$| –category (resp. a |$G$| –functor) is an object (resp. morphism) in |$\textrm{Cat}_{\infty ,G}:= \textrm{Fun}({\mathcal{O}}_{G}^{\textrm{op}},\textrm{Cat}_{\infty })$| and we will use the underline notation |$\underline{{\mathcal{D}}}$| to denote a |$G$| –category and |${\mathcal{D}}_{H}$| for its value at |$G/H\in{\mathcal{O}}_{G}^{\textrm{op}}$|⁠ . For subgroups |$K\leq H$| of |$G$|⁠ , we should think of the datum |${\mathcal{D}}_{H}\rightarrow{\mathcal{D}}_{K}$| packaged in the |$G$| –category |$\underline{{\mathcal{D}}}$| as a “restriction” functor |$\textrm{Res}^{H}_{K}$|⁠ . In particular, by definition of morphisms in functor categories, a |$G$| –functor is always compatible with these “restriction” maps. Important examples of |$G$| –categories include genuine |$G$| –spaces |$\{\underline{{\mathcal{S}}}_{G} \colon G/H \mapsto{\mathcal{S}}_{H}\}$| and genuine |$G$| –spectra |$\{\underline{\textrm{Sp}}_{G}\colon G/H\mapsto \textrm{Sp}_{H}\}$|⁠ . Additionally, the functor |${\mathcal{O}}_{H}\simeq ({\mathcal{O}}_{G})_{/(G/H)}\rightarrow ({\mathcal{O}}_{G})_{/(G/G)}\simeq{\mathcal{O}}_{G}$| induces a functor |$\textrm{Cat}_{\infty ,G}\rightarrow \textrm{Cat}_{\infty ,H}$| via restriction, which we denote by |$\textrm{Res}^{G}_{H}$|⁠ . Using Lurie’s notion of relative adjunctions [ 17 , §7.3.2], one can define the notion of |$G$| –adjunctions (cf. [ 27 , Def. 8.3]): this roughly means a pair of |$G$| –functors |$L\colon \underline{{\mathcal{C}}}\rightleftharpoons \underline{{\mathcal{D}}}: R$| together with the data of adjunctions when evaluated at each |$G/H\in{\mathcal{O}}_{G}^{\textrm{op}}$|⁠ .

Central to this theory is the notion of |$G$| –(co)limits, and among these the special cases of indexed (co)products find a distinguished place. In this article, we will only need these special cases, and so we briefly explain them now. Intuitively, they should be thought of as taking (co)products with respect to finite |$G$| –sets so that for example, for |$\underline{{\mathcal{C}}}\in \textrm{Cat}_{\infty ,G}$|⁠ , |$H\leq G$| and a |$H$| –equivariant object |$X \in{\mathcal{C}}_{H}$|⁠ , |$\prod _{G/H}X$| is now a |$G$| –equivariant object. We refer the reader to [ 27 , §5] for more details on this. When |$\underline{{\mathcal{C}}}$| is pointed (which just means that |${\mathcal{C}}_{K}$| is pointed for every |$K\leq G$| and all the restriction maps preserve the zero objects), one can construct a canonical comparison map |$\coprod _{G/H}\rightarrow \prod _{G/H}$| (cf. [ 20 , Cons. 5.2]). If this map is an equivalence, then we say that |$\underline{{\mathcal{C}}}$| is |$G$| –semiadditive. As in the nonequivariant case, for a |$G$| –category |$\underline{{\mathcal{C}}}$| with finite indexed products, we may construct (see for instance [ 20 , Def. 5.9]) the |$G$| –semiadditive |$G$| –category |$\underline{\textrm{CMon}}_{G}(\underline{{\mathcal{C}}})$| of |$G$| –commutative monoids in |$\underline{{\mathcal{C}}}$| whose objects should roughly be thought of as objects |$M\in \underline{{\mathcal{C}}}$| equipped with “equivariant addition maps” |$\prod _{G/H}\textrm{Res}^{G}_{H}M\rightarrow M$| for all |$H\leq G$| on top of the usual addition maps |$M\times M\rightarrow M$|⁠ . Observe that this version of the equivariant addition maps recovers the one mentioned in Notation 1.2 upon applying |$(-)^{G}$| since |$M^{H}\simeq (\prod _{G/H}\textrm{Res}^{G}_{H}M)^{G} \rightarrow M^{G}$|⁠ .

Now, denote by |$\underline{\textrm{Fin}}_{*}$| for the |$G$| –category of finite pointed |$G$| –sets. That is, it is the |$G$| –category |$\{G/H\mapsto \textrm{Fin}_{*H}:= \textrm{Fun}(BH, \textrm{Fin}_{*})\}$| where |$BH$| is the groupoid with one object and morphism set given by the group |$H$|⁠ . Nardin used this to give a definition of |$G$| –symmetric monoidal categories in [ 21 , |$\S 3$| ] much like the nonequivariant situation from [ 17 ]. See also [ 22 , §2] for a comprehensive, more recent treatment and [ 25 , §5.1] for a summary of these matters. Suffice to say, in this setting, a |$G$| –symmetric monoidal category is a |$G$| –category |$\underline{{\mathcal{D}}}^{\underline{\otimes }}$| equipped with a map to |$\underline{\textrm{Fin}}_{*}$| satisfying appropriate cocartesianness and |$G$| –operadic conditions, and |$G$| – |$\mathbb{E}_{\infty }$| –ring objects |$\textrm{CAlg}_{G}(\underline{{\mathcal{D}}}^{\underline{\otimes }}):= \textrm{Fun}_{G/\underline{\textrm{Fin}}_{*}}^{\textrm{int}}(\underline{\textrm{Fin}}_{*}, \underline{{\mathcal{D}}}^{\underline{\otimes }})$| are then |$G$| –inert sections to this map (see also Recollection   A.21 for slightly more details to this). An object |$R\in \textrm{CAlg}_{G}(\underline{{\mathcal{D}}}^{\underline{\otimes }})$| should be thought of as an object |$R\in \textrm{CAlg}({\mathcal{D}}_{G}^{\otimes })$| equipped with |$\mathbb{E}_{\infty }$| –algebra maps |$\bigotimes ^{G}_{H}\textrm{Res}^{G}_{H}R\rightarrow R$| encoding “equivariant multiplication”. In this notation, |$\textrm{CAlg}_{G}(\underline{\textrm{Sp}}_{G}^{\underline{\otimes }})$| will therefore mean those |$\mathbb{E}_{\infty }$| –rings in genuine |$G$| –spectra equipped with multiplicative norms, to be contrasted with objects in |$\textrm{CAlg}(\textrm{Sp}_{G}^{\otimes })$|⁠ , which do not have norms. Moreover, following [ 15 ], we use the notation |$\textrm{N}^{G}_{H}$| instead of |$\bigotimes ^{G}_{H}$| in the special case of |$\textrm{Sp}_{G}$|⁠ .

Analogously to Notation 2.2 , denoting by |$\underline{{\mathcal{C}}}^{\underline{\times }}$| the |$G$| –cartesian symmetric monoidal structure on a |$G$| –category |$\underline{{\mathcal{C}}}$|⁠ , which admits finite indexed products, we also have that |$\textrm{CAlg}_{G}(\underline{{\mathcal{C}}}^{\underline{\times }})\simeq \textrm{CMon}_{G}(\underline{{\mathcal{C}}})$|⁠ . This is essentially because for |$M\in \textrm{CAlg}_{G}(\underline{{\mathcal{C}}}^{\underline{\times }})$|⁠ , the structure |$\prod _{G/H}\textrm{Res}^{G}_{H}M= \bigotimes ^{G}_{H}\textrm{Res}^{G}_{H}M\rightarrow M$| supplies precisely the “equivariant addition” structure to be an object in |$\textrm{CMon}_{G}(\underline{{\mathcal{C}}})$|⁠ . While this is a folklore result, we have not been able to find a proof of this in the literature and so we have indicated a proof in the appendix, see Proposition A.23 , where we also give more precise explanations and references for some of the matters discussed above.

The |$G$| –adjunction |${\mathbb{S}}_{G}[-] \colon \underline{{\mathcal{S}}}_{G}\rightleftharpoons \underline{\textrm{Sp}}_{G}: {\Omega }^{\infty }_{G}$| induces an adjunction |${\mathbb{S}}_{G}[-] \colon{\textrm{CMon}}_{G}(\underline{{\mathcal{S}}}_{G}) \rightleftarrows{\textrm{CAlg}}_{G}(\underline{\textrm{Sp}}_{G}^{\underline{\otimes }}): {\Omega }^{\infty }_{G}$|⁠ .

We know by [ 21 , |$\S 3$| ] that the map |${\mathbb{S}}_{G}[-]$| refines to a |$G$| –symmetric monoidal functor |${\mathbb{S}}_{G}[-] \colon \underline{{\mathcal{S}}}_{G}^{\underline{\times }}\longrightarrow \underline{\textrm{Sp}}_{G}^{\underline{\otimes }}$|⁠ . This means that |${\Omega }^{\infty }_{G}$| canonically refines to a |$G$| –lax symmetric monoidal functor. Hence using that |${\textrm{CAlg}}_{G}(\underline{{\mathcal{S}}}_{G}^{\underline{\times }})\simeq{\textrm{CMon}}_{G}(\underline{{\mathcal{S}}}_{G})$| from Proposition A.23 and [ 16 , Lem. 1.3.11] that applying |$\textrm{CAlg}_{G}$| yields another adjunction analogously to [ 17 , Rmk. 7.3.2.13], we get the desired adjunction.

As explained for instance in [ 11 , §1], it makes sense to speak of objects in arbitrary semiadditive categories (or preadditive , as it was termed in that paper) having the property of being group–complete by requiring a certain canonically constructed shear map to be an equivalence. In the case of the semiadditive category |$\textrm{CMon}({\mathcal{S}})$|⁠ , we will write |$\textrm{CGrp}({\mathcal{S}})$| for the full subcategory of group–complete objects. One characterisation for some |$M\in \textrm{CMon}({\mathcal{S}})$| to lie in |$\textrm{CGrp}({\mathcal{S}})$| is that the abelian monoid |$\pi _{0}M$| has the property of being a group.

In order to state and prove the theorem, we will need a few more terminologies and observations.

  Notation 3.1. In this note, two kinds of ring localisations will feature and we define and relate them here. Let |$R\in \textrm{CAlg}(\textrm{Sp}_{G})$| and |$\underline{S} = \{S_{H}\}_{H\leq G}$| be a |$G$| –subset of the zeroth equivariant homotopy Mackey functor |$\underline{\pi }_{0}R$| of |$R$|⁠ . That is, for any |$H\leq G$|⁠ , |$\underline{S}$| satisfies |$\textrm{Res}^{G}_{H}S_{G}\subseteq S_{H}\subseteq \pi _{0}^{H}R:= \pi _{0}R^{H}$|⁠ . Now for any |$A\in \textrm{CAlg}(\textrm{Sp}_{G})$|⁠ , we define $$\begin{align*} &\textrm{Map}_{\textrm{CAlg}(\textrm{Sp}_{G})}^{\underline{S}^{-1}}(R,A) \quad\quad\ \textrm{and}\ \quad\quad \textrm{Map}_{\textrm{CAlg}(\textrm{Sp}_{G})}^{S_{G}^{-1}}(R,A)\end{align*}$$ to be subcomponents of |$\textrm{Map}_{\textrm{CAlg}(\textrm{Sp}_{G})}(R,A)$| of |$\mathbb{E}_{\infty }$| –algebra maps |$R\rightarrow A$|⁠ , which send elements in |$\underline{S}$| to units in |$\underline{\pi }_{0}A$| and send elements in |$S_{G}$| to units in |$\pi _{0}^{G}A$|⁠ , respectively. By general theory (cf. [ 23 , Appen. A] for example), we know that the latter mapping space is corepresented by a telescopic localisation |$S_{G}^{-1}R$| of |$R$| against elements in |$S_{G}\subseteq \pi _{0}^{G}R$| (i.e., |$\textrm{Map}_{\textrm{CAlg}(\textrm{Sp}_{G})}^{S_{G}^{-1}}(R,A)\simeq \textrm{Map}_{\textrm{CAlg}(\textrm{Sp}_{G})}(S_{G}^{-1}R,A)$|⁠ ). In particular, we have that |$\underline{\pi }_{\star }S_{G}^{-1}R\cong S_{G}^{-1}\underline{\pi }_{\star }R$|⁠ . On the other hand, if the former mapping space is corepresentable, then we will write the corepresenting object as |$L_{\underline{S}^{-1}}R$|⁠ . In general, this need not be given by a nice formula in terms of a telescopic localisation since we need to invert different sets of elements at different subgroups |$H\leq G$| that do not all come from restricting elements from |$S_{G}$| (i.e., the inclusion |$\textrm{Res}^{G}_{H}S_{G}\subseteq S_{H}$| might be proper), and so |$\underline{\pi }_{*}L_{\underline{S}^{-1}}R$| need not admit a nice description as a Mackey functor with elements in |$\underline{S}$| inverted. However, since maps |$R\rightarrow A$| that invert |$\underline{S}$| must necessarily invert |$S_{G}$|⁠ , we do have an inclusion $$\begin{align*} &\textrm{Map}_{\textrm{CAlg}(\textrm{Sp}_{G})}^{\underline{S}^{-1}}(R,-) \hookrightarrow \textrm{Map}_{\textrm{CAlg}(\textrm{Sp}_{G})}^{S_{G}^{-1}}(R,-).\end{align*}$$ Thus, when |$L_{\underline{S}^{-1}}R$| exists, this inclusion is induced by a canonical comparison map in |$\textrm{CAlg}(\textrm{Sp}_{G})$| $$\begin{align}& S_{G}^{-1}R \longrightarrow L_{\underline{S}^{-1}}R.\end{align}$$ (4)

Let |$M\in \textrm{CMon}({\mathcal{S}}_{G})$|⁠ . We write |$\underline{\pi }_{M}\subseteq \underline{\pi }_{0}{\mathbb{S}}_{G}[M]$| for the image of the Hurewicz map on the equivariant homotopy groups |$\underline{\pi }_{0}M \rightarrow \underline{\pi }_{0}{\Omega }^{\infty }_{G}{\mathbb{S}}_{G}[M] = \underline{\pi }_{0}{\mathbb{S}}_{G}[M]$| induced by the adjunction unit |$\textrm{id}\Rightarrow \Omega ^{\infty }_{G}{\mathbb{S}}_{G}$|⁠ . This is clearly a |$G$| –subset in the sense defined above.

We are now ready to state the main theorem of this note:

• (i) The object |$L_{(\underline{\pi }_{M})^{-1}}{\mathbb{S}}_{G}[M]$| exists and the group–completion map |$M \rightarrow \Omega BM$| induces an equivalence in |$\textrm{CAlg}({\textrm{Sp}}_{G})$| $$\begin{align*} &L_{(\underline{\pi}_{M})^{-1}}{\mathbb{S}}_{G}[M] \stackrel{\simeq}{\longrightarrow} {\mathbb{S}}_{G}[\Omega BM]\end{align*}$$
• (ii) Moreover, if |$M$| additionally has the structure of a |$G$| – |$\mathbb{E}_{\infty }$| –monoid |$G$| –space—that is, |$M\in \textrm{CMon}_{G}({{\mathcal{S}}}_{G})$| —then |${\mathbb{S}}_{G}[\Omega BM]\simeq L_{(\underline{\pi }_{M})^{-1}}{\mathbb{S}}_{G}[M] $| refines to a |$G$| – |$\mathbb{E}_{\infty }$| –ring object. In other words, it lifts to an object in |$\textrm{CAlg}_{G}({\textrm{Sp}}_{G})$|⁠ . Furthermore, in this case, the canonical map from ( 4 ) $$\begin{align*} &(\pi_{M}^{G})^{-1}{\mathbb{S}}_{G}[M] \longrightarrow L_{(\underline{\pi}_{M})^{-1}}{\mathbb{S}}_{G}[M]\simeq{\mathbb{S}}_{G}[\Omega BM] \end{align*}$$ is an equivalence so that we have the expected localisation effect on homotopy groups, that is, |$\underline{\pi }_{\star }{\mathbb{S}}_{G}[\Omega BM]\cong (\pi _{M}^{G})^{-1}\underline{\pi }_{\star }{\mathbb{S}}_{G}[M]$|⁠ .

We now turn to the proof of the first part of the theorem. We emphasise again that the theory of |$G$| –categories is not required in this part.

We now turn to the task of refining to normed structures when the input is more highly structured, that is, when |$M\in \textrm{CMon}_{G}(\underline{{\mathcal{S}}}_{G})$|⁠ . Before that, it would be useful to formulate the following intermediate notion together with a couple of easy consequences that would help us identify the homotopy groups of the abstract localisation we have so far.

Let |$R\in \textrm{CAlg}(\textrm{Sp}_{G})$| and |$\underline{S}\subseteq \underline{\pi }_{0}R$| be a |$G$| –subset of the zeroth equivariant homotopy groups of |$R$|⁠ . We say that |$\underline{S}$| satisfies the torsion–extension condition if for any |$H\leq G$|⁠ , the inclusion |$\textrm{Res}^{G}_{H}S_{G}\subseteq S_{H}$| is a torsion–extension, that is, for any |$a\in S_{H}$|⁠ , there exists a |$r\in \pi _{0}^{H}R$| such that |$r\cdot a\in \textrm{Res}^{G}_{H}S_{G}$|⁠ .

The reason for this choice of terminology was an analogy in the case of modules: if |$I\subseteq J\subseteq R$| are |$R$| –submodules satisfying the analogous condition, then |$J/I$| is a torsion |$R$| –module. In any case, the next three lemmas should clarify our interest in this condition.

If |$R\in \textrm{CAlg}({\textrm{Sp}}_{G})$| and |$\underline{S}\subseteq \underline{\pi }_{0}R$| is a multiplicatively closed |$G$| –subset satisfying Condition 3.4 , then |$L_{\underline{S}^{-1}}R$| exists and the canonical map |$S_{G}^{-1}R \longrightarrow L_{\underline{S}^{-1}}R$| from ( 4 ) is an equivalence. Furthermore, in this case, for any |$K\leq G$|⁠ , we have that |$\textrm{Res}^{G}_{K}S^{-1}_{G}R\simeq S^{-1}_{K}\textrm{Res}^{G}_{K}R$|⁠ .

As explained in Notation 3.1 , the canonical map in the statement induces an inclusion of subcomponents |$\textrm{Map}_{\textrm{CAlg}(\textrm{Sp}_{G})}^{\underline{S}^{-1}}(R, A) \hookrightarrow \textrm{Map}_{\textrm{CAlg}(\textrm{Sp}_{G})}^{S_{G}^{-1}}(R,A)$|⁠ . Hence, all we have to do is to show that all components in the target are hit. So suppose |$\varphi \colon R\rightarrow A$| inverts elements in |$S_{G}$|⁠ . We need to show that for all |$H\leq G$|⁠ , |$\varphi |_{H}\colon \textrm{Res}^{G}_{H}R\rightarrow \textrm{Res}^{G}_{H}A$| sends elements in |$S_{H}\subseteq \pi _{0}^{H}R$| to units in |$\pi _{0}^{H}A$|⁠ .

Thus, fix |$H\leq G$| and let |$a\in S_{H}$|⁠ . By hypothesis, there exists an |$r\in \pi _{0}^{H}R$| such that |$r\cdot a \in \textrm{Res}^{G}_{H}S_{G}$|⁠ . Since |$\varphi |_{H}$| inverts |$r\cdot a$|⁠ , let |$x\in \pi _{0}^{H}A$| such that |$1 = x\cdot \varphi |_{H}(r\cdot a) = x\cdot \varphi |_{H}(r)\cdot \varphi |_{H}(a)$|⁠ . In particular, since everything is commutative, |$x\cdot \varphi |_{H}(r)$| is the inverse of |$\varphi |_{H}(a)$|⁠ , and so |$\varphi |_{H}$| inverts |$a$| too. Therefore, since |$a$| was arbitrary, we see that |$\varphi |_{H}$| must have inverted all of |$S_{H}$| as required.

For the last statement, first observe that |$\textrm{Res}^{G}_{K}S^{-1}_{G}R\simeq (\textrm{Res}^{G}_{K}S_{G})^{-1}\textrm{Res}^{G}_{K}R$|⁠ . Hence, since |$\textrm{Res}^{G}_{K}S_{G}\subseteq S_{K}\subseteq \pi _{0}^{K}R$|⁠ , we see that a priori |$\textrm{Res}^{G}_{K}S^{-1}_{G}R$| has inverted possibly fewer elements than has |$S^{-1}_{K}\textrm{Res}^{G}_{K}R$|⁠ . However, the same argument as in the previous paragraph shows that under our hypothesis on |$R$|⁠ , we indeed have |$\textrm{Res}^{G}_{K}S^{-1}_{G}R\simeq S^{-1}_{K}\textrm{Res}^{G}_{K}R$| as wanted.

Let |$R\in \textrm{CAlg}_{G}(\underline{\textrm{Sp}}_{G})$| be a |$G$| – |$\mathbb{E}_{\infty }$| –ring object and |$\underline{S}\subseteq \underline{\pi }_{0}R$| be a |$G$| –subset that is closed under the norms. Then |$\underline{S}$| satisfies Condition 3.4 .

  Proof. Fix |$H\leq G$| and let |$a\in S_{H}$|⁠ . We want to show that there is an |$r\in \pi _{0}^{H}R$| such that |$r\cdot a\in \textrm{Res}^{G}_{H}S_{G}$|⁠ . For this, consider |$\textrm{N}^{G}_{H}a\in \pi _{0}^{G}R$|⁠ , which is in fact in |$S_{G}\subseteq \pi _{0}^{G}R$| by the norm–closure hypothesis. Then by the norm double coset formula, we get $$\begin{align*} &\textrm{Res}^{G}_{H}\textrm{N}^{G}_{H}a = \prod_{g\in H\backslash G/H} \textrm{N}^{H}_{H^{g}\cap H}g_{*}\textrm{Res}^{H}_{H\cap H^{g}}a \in \textrm{Res}^{G}_{H}S_{G},\end{align*}$$ where |$a$| is a factor on the right (i.e., when |$g=e$|⁠ ), whence the claim.

If |$M\in \textrm{CMon}_{G}(\underline{{\mathcal{S}}}_{G})$|⁠ , then |$\underline{\pi }_{M}\subseteq \underline{\pi }_{0}{\mathbb{S}}_{G}[M]$| is closed under the norms.

We now cash in all the work we have done to complete the proof of the theorem.

The norm closure of the subset |$\underline{\pi }_{M}\subseteq \underline{\pi }_{0}{\mathbb{S}}_{G}[M]$| from Lemma 3.8 should have indicated why the localisation |$(\underline{\pi }_{M})^{-1}{\mathbb{S}}_{G}[M]$| even had a chance of attaining the multiplicative norms. In general, a localisation on a |$G$| – |$\mathbb{E}_{\infty }$| –ring need not refine again to a |$G$| – |$\mathbb{E}_{\infty }$| –ring, as is well documented for instance in [ 14 ]. Nonetheless, the norm closure of a multiplicative subset is a necessary and sufficient property for the localisation to refine to the structure of a |$G$| – |$\mathbb{E}_{\infty }$| –ring. This can be deduced for example from [ 25 , Lem. 5.27].

Finally, we use Theorem 3.3 to quickly deduce Theorem 1.3 .

  Proof of Theorem 1.3 . Let |$K\leq G$| and |$\underline{N}$| a |$G$| –Mackey functor, thought of as an Eilenberg–Mac Lane genuine |$G$| –spectrum (see e.g., [ 26 , Ex. 4.41]). Then by definition of |$RO(G)$| –graded Bredon homology ( loc. cit. ), we have |$H_{\star }^{K}(\Omega BM; \underline{N}) = \pi _{\star }^{K}\big (\underline{N}\otimes{\mathbb{S}}_{G}[\Omega BM]\big )$|⁠ . Moreover, by the second part of Lemma 3.6 , we know that |$\textrm{Res}^{G}_{K}(\pi ^{G}_{M})^{-1}{\mathbb{S}}_{G}[M]\simeq (\pi ^{K}_{M})^{-1}\textrm{Res}^{G}_{K}{\mathbb{S}}_{G}[M]$| and so we get $$\begin{align*} &H_{\star}^{K}(M; \underline{N})[(\pi_{0}^{K}M)^{-1}] = (\pi^{K}_{M})^{-1}\pi^{K}_{\star}\big(\underline{N}\otimes{\mathbb{S}}_{G}[M]\big) \cong\pi^{K}_{\star}\big(\underline{N}\otimes (\pi^{G}_{M})^{-1}{\mathbb{S}}_{G}[M]\big)\end{align*}$$ whence the result by Theorem 3.3 .

In this last section, we will comment on three points:

We analyse the geometric fixed points of the abstract localisation from Notation 3.1 and show that it has an easy description,

we explain a generic situation where the theorem might be applied,

and we give a plentiful source of examples of |$G$| – |$\mathbb{E}_{\infty }$| –monoid |$G$| –spaces.

For the first point, as we have remarked in Notation 3.1 , the abstract localisation |$L_{\underline{S}^{-1}}R$|⁠ , if it exists, has no reason to have a nice description in general. Notwithstanding, it does interact well with the geometric fixed points, as we now explain.

  Observation 4.1. Let |$\underline{S}\subseteq \underline{\pi }_{0}R$| be a multiplicative |$G$| –subset for some |$R\in \textrm{CAlg}(\textrm{Sp}_{G})$|⁠ . Recall for instance from [ 18 , Cons. 6.10, Thm. 6.11] that we have a lax symmetric monoidal Bousfield localisation |$\Phi ^{G} \colon \textrm{Sp}_{G} \rightleftharpoons \textrm{Sp} \:: \Xi ^{G}$|⁠ , which then induces a Bousfield localisation |$\Phi ^{G} \colon \textrm{CAlg}(\textrm{Sp}_{G}) \rightleftharpoons \textrm{CAlg}(\textrm{Sp}) \:: \Xi ^{G}$|⁠ . Here for |$X\in \textrm{Sp}$|⁠ , |$\Xi ^{G}X$| is the |$G$| –spectrum such that |$(\Xi ^{G}X)^{G}\simeq X$| and |$(\Xi ^{G}X)^{H}\simeq 0$| for |$H\lneq G$|⁠ . Classically, this is also written as |$\widetilde{E\mathcal{P}}\otimes X$| where |$\mathcal{P}$| is the proper family of subgroups of |$G$|⁠ . We claim that the resulting equivalence |$\textrm{Map}_{\textrm{CAlg}(\textrm{Sp}_{G})}(R,\Xi ^{G}A)\simeq \textrm{Map}_{\textrm{CAlg}(\textrm{Sp})}(\Phi ^{G}R,A)$| restricts to an equivalence $$\begin{align*} &\textrm{Map}_{\textrm{CAlg}(\textrm{Sp}_{G})}^{\underline{S}^{-1}}(R,\Xi^{G}A)\simeq \textrm{Map}_{\textrm{CAlg}(\textrm{Sp})}^{(\Phi^{G}S_{G})^{-1}}(\Phi^{G}R,A).\end{align*}$$ To see this, since |$\Phi ^{G}\Xi ^{G}\simeq \textrm{id}$|⁠ , we know |$\Phi ^{G}$| induces an inclusion $$\begin{align*} &\textrm{Map}_{\textrm{CAlg}(\textrm{Sp}_{G})}^{\underline{S}^{-1}}(R,\Xi^{G}A) \hookrightarrow\textrm{Map}_{\textrm{CAlg}(\textrm{Sp})}^{(\Phi^{G}S_{G})^{-1}}(\Phi^{G}R,A). \end{align*}$$ To see that this is even an equivalence, suppose we have |$\varphi \colon \Phi ^{G}R\rightarrow A$|⁠ , which inverts |$\Phi ^{G}S_{G}\subseteq \pi _{0}\Phi ^{G}R$|⁠ . The adjoint |$\overline{\varphi } \colon R\rightarrow \Xi ^{G}A$| is given by the composite $$\begin{align*} &\overline{\varphi} \colon R \stackrel{\eta}{\longrightarrow} \Xi^{G}\Phi^{G}R \stackrel{\Xi^{G}\varphi}{\longrightarrow} \Xi^{G}A,\end{align*}$$ where the adjunction unit |$\eta $| is a map of |$\mathbb{E}_{\infty }$| –rings and sends elements in |$S_{G}$| to elements in |$\Phi ^{G}S_{G}$|⁠ . Therefore, |$\overline{\varphi }$| must invert all elements in |$S_{G}$|⁠ . Moreover, since for |$H\lneq G$|⁠ , |$(\Xi ^{G}A)^{H}$| are equivalent to the zero rings, the maps |$\textrm{Res}^{G}_{H}\overline{\varphi } \colon \textrm{Res}^{G}_{H}R \rightarrow \textrm{Res}^{G}_{H}\Xi ^{G}A\simeq 0$| send everything to units for trivial reasons, and so in total |$\overline{\varphi }$| indeed inverts elements in |$\underline{S}$| as was to be shown.

Let |$R\in \textrm{CAlg}(\textrm{Sp}_{G})$|⁠ , |$\underline{S}\subseteq \underline{\pi }_{0}R$| a multiplicative subset, and suppose |$L_{\underline{S}^{-1}}R$| exists. Then the canonical map |$\Phi ^{G}R\rightarrow \Phi ^{G}L_{\underline{S}^{-1}}R$| induces an equivalence |$(\Phi ^{G}S_{G})^{-1}\Phi ^{G}R\simeq \Phi ^{G}L_{\underline{S}^{-1}}R$|⁠ .

  Proof. Let |$A\in \textrm{CAlg}(\textrm{Sp})$|⁠ . Then $$\begin{align*} \begin{split} \textrm{Map}_{\textrm{CAlg}(\textrm{Sp})}(\Phi^{G}L_{\underline{S}^{-1}}R,A) & \simeq \textrm{Map}_{\textrm{CAlg}(\textrm{Sp}_{G})}(L_{\underline{S}^{-1}}R, \Xi^{G} A)\\ &\simeq \textrm{Map}_{\textrm{CAlg}(\textrm{Sp}_{G})}^{\underline{S}^{-1}}(R,\Xi^{G}A)\\ &\simeq \textrm{Map}_{\textrm{CAlg}(\textrm{Sp})}^{(\Phi^{G}S_{G})^{-1}}(\Phi^{G}R,A)\\ &\simeq \textrm{Map}_{\textrm{CAlg}(\textrm{Sp})}((\Phi^{G}S_{G})^{-1}\Phi^{G}R,A),\\ \end{split} \end{align*}$$ where the third equivalence is by Observation 4.1 .

Next, we turn to the matter of recording a generic toy situation where our theorem might be useful. This manoeuvre is an immediate generalisation of its (standard) nonequivariant analogue.

Suppose we have a map |$f\colon X\rightarrow Y $| of |$G$| –spaces, which induces an equivalence |${\mathbb{S}}_{G}f\colon{\mathbb{S}}_{G}[X]\rightarrow{\mathbb{S}}_{G}[Y]$|⁠ . Suppose moreover that |$X, Y$| are both |$G$| –simply–connected (i.e., |$X^{H}$| and |$Y^{H}$| are simply–connected for all |$H\leq G$|⁠ ). Then the map |$f\colon X\rightarrow Y$| was already a |$G$| –equivalence.

To see this, we need to show that we have an equivalence for all fixed points. So let |$H\leq G$|⁠ . Applying the |$H$| –geometric fixed points |$\Phi ^{H}$| to the equivalence |${\mathbb{S}}_{G}f$| gives us an equivalence |$\Phi ^{H}{\mathbb{S}}_{G}f\simeq{\mathbb{S}}[f^{H}]\colon{\mathbb{S}}[X^{H}]\stackrel{\simeq }{\longrightarrow } {\mathbb{S}}[Y^{H}]$|⁠ . Hence, by the ordinary simply–connected homology Whitehead theorem, the map of spaces |$f^{H} \colon X^{H}\rightarrow Y^{H}$| is an equivalence, as was to be shown.

Our Theorem 3.3 can then potentially be used in conjunction with this in the following way. Suppose we have a map of |$G$| – |$\mathbb{E}_{\infty }$| –monoids |$N\rightarrow \Omega BM$| where we already understand |${\mathbb{S}}_{G}[N]$| and where |$\Omega BM$| and |$N$| are |$G$| –simply–connected. Since the theorem gives a formula for |${\mathbb{S}}_{G}[\Omega BM]$|⁠ , we might be able to use it to show that |${\mathbb{S}}_{G}[N]\rightarrow{\mathbb{S}}_{G}[\Omega BM]$| is an equivalence. If this were true, then by the equivariant Whitehead proposition above, we can deduce that |$N\rightarrow \Omega BM$| is an equivalence, thus giving a computation of |$\Omega BM$| in terms of |$N$|⁠ .

Of course, this toy situation might not be so applicable since |$G$| –simply connectedness is an unreasonable condition to demand in general. Our intention for this was only to indicate a template over which other variations might be beneficial in specific circumstances.

Lastly, we end the main body of this note by recording a huge standard source of potentially interesting examples of |$G$| – |$\mathbb{E}_{\infty }$| –monoid |$G$| –spaces to consider.

|$G$| – |$\mathbb{E}_{\infty }$| –monoid |$G$| –spaces, for which the localisation formula of Theorem 3.3 (ii) holds, are in abundant supply. One fertile source is small semiadditive |$\infty $| –categories (which include stable |$\infty $| –categories) equipped with |$G$| –actions, that is, objects in |$\textrm{Fun}(BG,\textrm{Cat}^{\oplus }_{\infty })$|⁠ . If |${\mathcal{C}}$| were one such instance, then |$\{{\mathcal{C}}^{hH}\}_{H\leq G}$| assembles to a |$G$| – |$\mathbb{E}_{\infty }$| –monoid |$G$| –category. In other words, it is an object in |$\textrm{Mack}_{G}(\textrm{Cat}_{\infty }^{\oplus })$| (cf. [ 3 , |$\S 8$| ] for an explanation of this). Then taking the groupoid core yields a |$G$| – |$\mathbb{E}_{\infty }$| –monoid |$G$| –space |$\{({\mathcal{C}}^{hH})^{\simeq }\}_{H\leq G}\in \textrm{Mack}_{G}({\mathcal{S}})\simeq \textrm{CMon}_{G}(\underline{{\mathcal{S}}}_{G})$|⁠ . In fact, this procedure of producing |$G$| – |$\mathbb{E}_{\infty }$| –monoid |$G$| –spaces by taking groupoid cores works more generally for any |$G$| –semiadditive |$G$| –category.

Concrete examples belonging to this template include equipping the trivial |$G$| –action on categories like finitely generated projective |$R$| –modules |$\textrm{Proj}_{R}$| for |$R\in \textrm{CRing}$| or perfect |$A$| –modules |$\textrm{Perf}_{A}$| for |$A\in \textrm{CAlg}(\textrm{Sp})$|⁠ . These yield the objects |$\{\textrm{Map}(BH, \textrm{Proj}_{R}^{\simeq })\}_{H\leq G}$| and |$\{\textrm{Map}(BH, \textrm{Perf}_{A}^{\simeq })\}_{H\leq G}$| in |$\textrm{CMon}_{G}(\underline{{\mathcal{S}}}_{G})$|⁠ , the group–completions of which give the so–called Swan equivariant K–theories. Familiar examples of |$G$| –spectra obtained in this manner include |$\textrm{ku}_{G}$| and |$\textrm{ko}_{G}$|⁠ . Another interesting source of semiadditive categories equipped with |$G$| –actions come from finite Galois extensions of fields |$K\subseteq L$|⁠ . In this case, the |$G$| –Galois action on |$\textrm{Vect}_{L}^{\textrm{fd}}$| yields the |$G$| – |$\mathbb{E}_{\infty }$| –monoid |$G$| –space |$\{(\textrm{Vect}_{L^{H}}^{\textrm{fd}})^{\simeq }\}_{H\leq G}$|⁠ .

We will provide in this appendix a proof of the folklore result that |$\textrm{CMon}_{G}(\underline{{\mathcal{C}}})\simeq \textrm{CAlg}_{G}(\underline{{\mathcal{C}}}^{\underline{\times }})$|⁠ , which heuristic intuition we explain at the end of Setting 2.4 . The proof will be a straightforward—if a bit tedious—adaptation of the proof by Lurie from [ 17 , Prop. 2.4.2.5] as organised by Chu and Haugseng [ 6 ] in the language of the so–called cartesian patterns . The main idea of Lurie’s proof is that there is a nice model for the cartesian symmetric monoidal structure that embeds inside a larger category, which in turn admits a convenient universal property of being mapped into. In the interest of space and as this is a necessarily technical result, we will assume some familiarity with the formalism and underpinnings of parametrised homotopy theory (cf. [ 20 , 27 ]), as well as the associated factorisation system and operad theory as laid out in [ 28 , §3, §4] and [ 22 , §2.1–§2.3]. We will however provide basic recollections and precise references for the sake of comprehensibility. Lastly, we should also mention that this is an extremely brisk and minimalistic account sufficient for our purposes, and it might be interesting to investigate the notion of parametrised cartesian patterns along the level of generality in [ 6 ].

Our first order of business is to set up the basic theory of |$G$| –cartesian patterns and their associated monoids.

we write |$\underline{{\mathcal{C}}}_{H}$| for the |$H$| –category |$\textrm{Res}^{G}_{H}\underline{{\mathcal{C}}}$|⁠ . Note that this does not conflict with the notation |${\mathcal{C}}_{H}$| from Setting 2.4 . As such, we will also write |$H$| –objects as |$X\in \underline{{\mathcal{C}}}_{H}$|⁠ ,

we will write |$\underline{{\mathcal{C}}}_{X/}$| to mean the |$H$| –category |$(\underline{{\mathcal{C}}}_{H})_{X/}$|⁠ ,

for a |$G$| –functor |$\underline{{\mathcal{D}}}\rightarrow \underline{{\mathcal{C}}}$|⁠ , we will write |$\underline{{\mathcal{D}}}_{X}$| for the |$H$| –category |$\underline{\ast }\times _{\underline{{\mathcal{C}}}_{H}}\underline{{\mathcal{D}}}_{H}$|⁠ , where |$\underline{\ast }\rightarrow \underline{{\mathcal{C}}}_{H}$| is the |$H$| –functor picking out |$X$|⁠ .

Let |$\underline{{\mathcal{O}}}\in \textrm{Cat}_{G}$|⁠ . A |$G$| –algebraic pattern structure on |$\underline{{\mathcal{O}}}$| is a |$G$| –factorisation system (i.e., a fibrewise factorisation system closed under the restriction functors, cf. [ 28 , Def. 3.1]) on |$\underline{{\mathcal{O}}}$| together with a collection of objects that are termed elementary objects . We term the left (resp. right) class as the fibrewise inert (resp. fibrewise active) morphisms. A morphism of |$G$| –algebraic patterns is a |$G$| –functor |$\underline{{\mathcal{O}}}\rightarrow \underline{{\mathcal{P}}}$|⁠ , which preserves the fibrewise inert and active morphisms as well as the elementary objects. Write |$\underline{{\mathcal{O}}}^{\textrm{int}}$| for the subcategory of |$\underline{{\mathcal{O}}}$| containing only the fibrewise inert morphisms, and write |$\underline{{\mathcal{O}}}^{\textrm{el}}\subseteq \underline{{\mathcal{O}}}^{\textrm{int}}$| for the full subcategory of elementary objects and fibrewise inert morphisms.

Fix |$H\leq G$| and |$O\in \underline{{\mathcal{O}}}_{H}$| a |$H$| –object. Write |$\underline{{\mathcal{O}}}_{O/}^{\textrm{el}}:= \underline{{\mathcal{O}}}^{\textrm{el}}\times _{\underline{{\mathcal{O}}}^{\textrm{int}}}\underline{{\mathcal{O}}}_{O/}^{\textrm{int}}$| for the category of fibrewise inert maps from |$O$| to elementary objects, and morphisms are fibrewise inert maps between these.

We will follow Chu and Haugseng’s notation from [ 5 , 6 ] and use |$\rightarrowtail $| to denote inert maps and |$\rightsquigarrow $| to denote active maps.

This is the prime example of a |$G$| –algebraic pattern, using that algebraic patterns are closed under limits in |$\textrm{Cat}_{\infty }$| by [ 5 , Cor. 5.5]. Concretely, when |$K=H$|⁠ , the fibrewise inert maps are the ones where |$Z\rightarrow W$| is an equivalence, and the fibrewise active maps are those where the induced map |$Z\rightarrow U\times _{G/H}G/K$| is an equivalence (see [ 22 , Def. 2.1.3]); the elementary objects are the objects |$[G/H\xrightarrow{=}G/H]$| at level |$H $| for each |$H\leq G$|⁠ .

Following [ 5 , Def. 6.1], we may make the following:

We say that a morphism |$f\colon \underline{{\mathcal{O}}}\rightarrow \underline{{\mathcal{P}}}$| of |$G$| –algebraic patterns has unique lifting of fibrewise active morphisms if for every |$H\leq G$| and fibrewise active morphism |$\phi \colon P \rightarrow f(O)$| in |${{\mathcal{P}}}_{H}$|⁠ , the space of lifts of |$\phi $| to a fibrewise active morphism |$O^{\prime}\rightarrow O$| in |${{\mathcal{O}}}_{H}$| is contractible.

Since |$G$| –coinitiality is a fibrewise statement by the dual of [ 27 , Thm. 6.7] and Definition A.6 is also fibrewise, we may deduce immediately from [ 5 , Lem. 6.2] the following:

A morphism of |$G$| –algebraic patterns |$f\colon \underline{{\mathcal{O}}}\rightarrow \underline{{\mathcal{P}}}$| has unique lifting of fibrewise active morphisms if and only if for every |$H\leq G$| and all |$P\in{{\mathcal{P}}}_{H}$|⁠ , the functor |$\underline{{\mathcal{O}}}^{\textrm{int}}_{P/}\rightarrow \underline{{\mathcal{O}}}_{P/}$| is |$G$| –coinitial.

A |$G$| –cartesian pattern is a |$G$| –algebraic pattern |$\underline{{\mathcal{O}}}$| equipped with a morphism of |$G$| –algebraic patterns |$|-|\colon \underline{{\mathcal{O}}}\rightarrow \underline{\textrm{Fin}}_{*}$| such that for every |$H\leq G$| and |$O\in \underline{{\mathcal{O}}}_{H}$|⁠ , the induced map |$\underline{{\mathcal{O}}}^{\textrm{el}}_{O/}\rightarrow \underline{\textrm{Fin}}_{*,|O|/}^{\textrm{el}}$| is an equivalence. A morphism of |$G$| –cartesian patterns is a morphism of |$G$| –algebraic patterns over |$\underline{\textrm{Fin}}_{*}$|⁠ .

  Definition A.10 (“[ 6 , Def. 2.9]”). Let |$\underline{{\mathcal{O}}}$| be a |$G$| –cartesian pattern and suppose |$\underline{{\mathcal{C}}}$| has finite indexed products. A |$G$| –functor |$F\colon \underline{{\mathcal{O}}}\rightarrow \underline{{\mathcal{C}}}$| is said to be an |$\underline{{\mathcal{O}}}$| –monoid if for every |$[U\rightarrow G/H]\in \underline{\textrm{Fin}}_{*H}$| and |$O\in \underline{{\mathcal{O}}}_{H}$| lying over |$[U\rightarrow G/H]$|⁠ , writing |$U = \coprod _{j=1}^{n}U_{j}$| for the |$G$| –orbital decomposition, |$u_{j}\colon U_{j}\rightarrow G/H$| for the structure maps and |$\chi _{[U_{j}\subseteq U]}\colon O \rightarrow O_{j}$| with |$O_{j}$| lying over |$[U_{j}=U_{j}]$| afforded by the equivalence |$\underline{{\mathcal{O}}}^{\textrm{el}}_{O/}\xrightarrow{\simeq } \underline{\textrm{Fin}}_{*,|O|/}^{\textrm{el}}$|⁠ , the canonical map of |$H$| –objects in |$\underline{{\mathcal{C}}}$| $$\begin{align*} &F(O) \longrightarrow \prod_{j=1}^{n}u_{j*}F(O_{j})\end{align*}$$ is an equivalence. By the |$G$| –cartesian pattern condition, this is equivalent to the following: writing |$j\colon \underline{{\mathcal{O}}}^{\textrm{el}}\hookrightarrow \underline{{\mathcal{O}}}^{\textrm{int}}$| for the inclusion, |$F$| is an |$\underline{{\mathcal{O}}}$| –monoid if and only if the canonical map |$F|_{\underline{{\mathcal{O}}}^{\textrm{int}}}\rightarrow j_{*}j^{*}(F|_{\underline{{\mathcal{O}}}^{\textrm{int}}})$| is an equivalence. We write |$\textrm{Mon}_{\underline{{\mathcal{O}}}}(\underline{{\mathcal{C}}})\subseteq \textrm{Fun}_{G}(\underline{{\mathcal{O}}},\underline{{\mathcal{C}}})$| for the full subcategory of |$\underline{{\mathcal{O}}}$| –monoids in |$\underline{{\mathcal{C}}}$|⁠ .

In the case |$\underline{{\mathcal{O}}}=\underline{\textrm{Fin}}_{*}$|⁠ , by an easy comparison of definitions with [ 20 , Def. 5.9], we get that |$\textrm{Mon}_{\underline{\textrm{Fin}}_{*}}(\underline{{\mathcal{C}}})\simeq \textrm{CMon}_{G}(\underline{{\mathcal{C}}})$| where |$\textrm{CMon}_{G}(\underline{{\mathcal{C}}})$| is in the sense discussed in the body of the paper.

The exact same argument as in [ 5 , Prop. 6.3], which uses only formalities about Kan extensions such as fully faithfulness of Kan extensions along fully faithful functors [ 27 , Prop. 10.6] as well as Lemma A.7 , applies here to yield the following:

If |$f\colon \underline{{\mathcal{O}}}\rightarrow \underline{{\mathcal{P}}}$| is a morphism of |$G$| –algebraic patterns that has unique fibrewise active lifting, then the right Kan extension |$f_{*}\colon{\textrm{Fun}}_{G}(\underline{{\mathcal{O}}},\underline{{\mathcal{C}}})\rightarrow{\textrm{Fun}}_{G}(\underline{{\mathcal{P}}},\underline{{\mathcal{C}}})$| restricts to |$f_{*}\colon \textrm{Mon}_{\underline{{\mathcal{O}}}}(\underline{{\mathcal{C}}})\rightarrow \textrm{Mon}_{\underline{{\mathcal{P}}}}(\underline{{\mathcal{C}}})$|⁠ .

Next, we work towards constructing the equivariant generalisation of Lurie’s model [ 17 , Prop. 2.4.1.5] for the cartesian symmetric monoidal structure for a |$G$| –category with finite indexed products.

Observe also that for |$[U \rightarrow G/H]\in \underline{\textrm{Fin}}_{*H}$|⁠ , |$\underline{\Gamma }^{\underline{\times }}_{[U \rightarrow G/H]}$| is a |$H$| –category such that for any |$K\leq H$|⁠ , the fibre over |$H/K$| is given by the opposite of the poset of |$K$| –subsets of the |$H$| –set |$U$| (compare with [ 17 , Cons. 2.4.1.4]): this is because the fibrewise inert maps pick out the orbits in |$U$|⁠ .

  Construction A.14 (“[ 17 , Cons. 2.4.1.4]”). Applying [ 27 , Thm. 9.3 (2)] or [ 28 , Recoll. 4.3] to the |$G$| –cartesian fibration |$\textrm{ev}_{0}\colon \underline{\Gamma }^{\underline{\times }}\longrightarrow \underline{\textrm{Fin}}_{*}$| and the |$G$| –cocartesian fibration |$\underline{{\mathcal{C}}}\times \underline{\textrm{Fin}}_{*}\rightarrow \underline{\textrm{Fin}}_{*}$| we obtain a |$G$| –cocartesian fibration |$\overline{\underline{{\mathcal{C}}}}^{\underline{\times }}\rightarrow \underline{\textrm{Fin}}_{*}$|⁠ . By [ 28 , Thm. 4.9], this construction satisfies a universal property, which implies in particular that $$\begin{align}& \underline{\textrm{Fun}}_{/\underline{\textrm{Fin}}_{*}}(\underline{\textrm{Fin}}_{*},\underline{\overline{{\mathcal{C}}}}^{\underline{\times}})\simeq \underline{\textrm{Fun}}(\underline{\Gamma}^{\underline{\times}},\underline{{\mathcal{C}}})\end{align}$$ (A.2) Furthermore, by [ 27 , Prop. 9.7], we have $$\begin{equation*}\underline{\overline{{\mathcal{C}}}}^{\underline{\times}}_{[U\rightarrow G/H]}\simeq \underline{\textrm{Fun}}_{[U\rightarrow G/H]}\big(\underline{\Gamma}^{\underline{\times}}_{[U\rightarrow G/H]}, (\underline{{\mathcal{C}}}\times\underline{\textrm{Fin}}_{*})_{[U\rightarrow G/H]}\big)\simeq \underline{\textrm{Fun}}(\underline{\Gamma}^{\underline{\times}}_{[U\rightarrow G/H]}, \underline{{\mathcal{C}}}_{H}).\end{equation*}$$ If |$\underline{{\mathcal{C}}}$| has all finite indexed products, we define |$\underline{{\mathcal{C}}}^{\underline{\times }}$| to be the full subcategory of |$\overline{\underline{{\mathcal{C}}}}^{\underline{\times }}$| whose objects over |$[U\rightarrow G/H]$| are the |$H$| –functors |$F\colon \underline{\Gamma }^{\underline{\times }}_{[U\rightarrow G/H]}\rightarrow \underline{{\mathcal{C}}}_{H}$| such that for every |$K\leq H$| and |$K$| –object |$[U\rightarrowtail V]_{G/K}$| with |$G$| –orbit decomposition |$V = \coprod _{j=1}^{n} V_{j}$| and structure maps |$v_{j}\colon V_{j}\rightarrow G/K$|⁠ , the map $$\begin{align}& F([U\rightarrowtail V]_{G/K}) \longrightarrow \prod_{j=1}^{n}{v_{j*}}F([U\rightarrowtail V\rightarrowtail V_{j}]_{V_{j}})\end{align}$$ (A.3) induced by the characteristic maps |$\chi _{[V_{j}\subseteq V]}\colon V\rightarrowtail V_{j}$| is an equivalence. Now observe that, writing |$U= \coprod _{j}U_{j}$| for the |$G$| –orbital decomposition with structure maps |$u_{j}\colon U_{j}\rightarrow G/H$|⁠ , we have the full subcategory |$\coprod _{j}{u_{j!}}\underline{\ast }\subseteq \underline{\Gamma }^{\underline{\times }}_{[U\rightarrow G/H]}$| consisting of the single |$G$| –orbits of |$U$|⁠ . A straightforward unwinding of definitions show that |$\underline{{\mathcal{C}}}^{\underline{\times }}_{[U\rightarrow G/H]}\subseteq \underline{\overline{{\mathcal{C}}}}^{\underline{\times }}_{[U\rightarrow G/H]}$| is identified with the full subcategory $$\begin{align*} &\prod_{j}{u_{j*}}u_{j}^{*}\underline{{\mathcal{C}}} \simeq \underline{\textrm{Fun}}(\coprod_{j}{u_{j!}}\underline{\ast}, \underline{{\mathcal{C}}})\subseteq \underline{\textrm{Fun}}(\underline{\Gamma}^{\underline{\times}}_{[U\rightarrow G/H]},\underline{{\mathcal{C}}}_{H})\end{align*}$$ where the inclusion is by right Kan extension (compare with the proof of [ 17 , Prop. 2.4.1.5 (4)]). This in particular means that we have an identification |${{\mathcal{C}}}^{\underline{\times }}_{[U\rightarrow G/H]}\simeq \prod _{j}{\mathcal{C}}_{U_{j}}$|⁠ .

  Remark A.15. By [ 28 , Recoll. 4.3] and using that the cocartesian pushforward functors to the constant |$G$| –cocartesian fibration |$\underline{{\mathcal{C}}}\times \underline{\textrm{Fin}}_{*}\rightarrow \underline{\textrm{Fin}}_{*}$| are just the identity functors, we see that for a morphism of |$H$| –objects |$f\colon U \rightarrow V$| in |$\underline{\textrm{Fin}}_{*H}$|⁠ , the associated cocartesian pushforward functor on the |$G$| –cocartesian fibration |$\underline{\overline{{\mathcal{C}}}}^{\underline{\times }}\rightarrow \underline{\textrm{Fin}}_{*}$| looks like $$\begin{align*} &\underline{\textrm{Fun}}_{H}(\underline{\Gamma}^{\underline{\times}}_{[U\rightarrow G/H]}, \underline{{\mathcal{C}}}_{H})\longrightarrow \underline{\textrm{Fun}}_{H}(\underline{\Gamma}^{\underline{\times}}_{{[V\rightarrow G/H]}}, \underline{{\mathcal{C}}}_{H})\quad::\quad F \mapsto F\circ f^!,\end{align*}$$ where |$f^! \colon \underline{\Gamma }^{\underline{\times }}_{{[V\rightarrow G/H]}}\rightarrow \underline{\Gamma }^{\underline{\times }}_{[U\rightarrow G/H]}$| is the |$H$| –functor described in Construction A.13 .

Let |$\underline{{\mathcal{C}}}$| be a |$G$| –category with finite indexed products. The composite |$\underline{{\mathcal{C}}}^{\underline{\times }}\subseteq \overline{\underline{{\mathcal{C}}}}^{\underline{\times }}\rightarrow \underline{\textrm{Fin}}_{*}$| is a |$G$| –symmetric monoidal structure on the |$G$| –category |$\underline{{\mathcal{C}}}$|⁠ .

By the definition of |$G$| –symmetric monoidal categories [ 22 , Def. 2.1.7 and Def. 2.2.3], first note that it would suffice to show that the composite is a |$G$| –cocartesian fibration and that the characteristic maps associated to any orbital decomposition |$U = \coprod _{j=1}^{n}U_{j}$| induce equivalences |${{\mathcal{C}}}^{\underline{\times }}_{[U\rightarrow G/H]}\xrightarrow{\simeq }\prod _{j=1}^{n}{\mathcal{C}}_{U_{j}}$| since these two conditions together ensure that [ 22 , Def. 2.1.7 (3)] holds. The second point has been dealt with at the end of Construction A.14 and so we are left to show that the composite is indeed a |$G$| –cocartesian fibration.

Our next goal is to show that |$\underline{\Gamma }^{\underline{\times }}$| can be endowed with the structure of a |$G$| –cartesian pattern and to show in Lemma A.20 that its monoid theory is equivalent to that associated to |$\underline{\textrm{Fin}}_{*}$|⁠ .

There is a natural factorisation system on |$\underline{\Gamma }^{\underline{\times }}\subseteq \underline{\textrm{Fin}}_{*}^{\Delta ^{1}}$| where the fibrewise inert (resp. fibrewise active) morphisms are those that are pointwise fibrewise inert (resp. fibrewise active).

The exact same argument of [ 6 , Lem. 5.8] works here since that argument only uses composability of inert morphisms and uniqueness of the fibrewise inert–active factorisations, both of which are true in |$\underline{\textrm{Fin}}_{*}$|⁠ .

Let |$i\colon \underline{\textrm{Fin}}_{*}\hookrightarrow \underline{\Gamma }^{\underline{\times }}$| be the functor that takes a finite |$H$| –set |$U$|⁠ , for any |$H\leq G$|⁠ , to |$[U\xrightarrow{=}U]_{G/H}$|⁠ . In other words, it is the right Kan extension along the inclusion |$\{1\} \hookrightarrow \Delta ^{1}$| and hence is fully faithful by [ 27 , Prop. 10.6]. This is immediately seen to be a morphism of |$G$| –cartesian patterns. By the same argument as in [ 6 , Rmk. 5.13], which uses only the uniqueness of the fibrewise inert–active factorisation in |$\underline{\Gamma }^{\underline{\times }}$|⁠ , we see that |$i$| has unique lifting of fibrewise active morphisms in the sense of Definition A.6 .

Let |$\underline{{\mathcal{C}}}$| have finite indexed products. The adjunction |$i^{*} \colon \textrm{Mon}_{\underline{\Gamma }^{\underline{\times }}}(\underline{{\mathcal{C}}})\rightleftharpoons \textrm{Mon}_{\underline{\textrm{Fin}}_{*}}(\underline{{\mathcal{C}}}): i_{*}$| is an equivalence.

Lastly, we relate the notion of monoids explored so far with that of algebras, which we recall now.

The following lemma, which is an immediate modification of [ 6 , Lem. 5.15], will be the bridge connecting the theory of monoids and that of algebras.

Under the natural equivalence |$\underline{\textrm{Fun}}_{/\underline{\textrm{Fin}}_{*}}(\underline{\textrm{Fin}}_{*},\underline{\overline{{\mathcal{C}}}}^{\underline{\times }})\simeq \underline{\textrm{Fun}}(\underline{\Gamma }^{\underline{\times }},\underline{{\mathcal{C}}})$| from ( A.2 ), the full subcategory |$\textrm{Mon}_{\underline{\Gamma }^{\underline{\times }}}(\underline{{\mathcal{C}}})$| from the right-hand side is identified with |$\textrm{Fun}_{/\underline{\textrm{Fin}}_{*}}^{\textrm{int}}(\underline{\textrm{Fin}}_{*},\underline{{\mathcal{C}}}^{\underline{\times }})$| from the left-hand side.

• Writing the orbital decomposition |$W = \coprod _{j=1}^{n}W_{j}$| with structure maps |$w_{j}\colon W_{j}\rightarrow G/H$|⁠ , the canonical map $$\begin{align*} &F^{\prime}([U\rightarrowtail W]_{G/H})\longrightarrow \prod^{n}_{j=1}{w_{j*}}F^{\prime}([U\rightarrowtail W\rightarrowtail W_{j}]_{W_{j}})\end{align*}$$ is an equivalence.
• For every |$H$| –inert map |$Y\rightarrowtail U$| in |$\underline{\textrm{Fin}}_{*}$|⁠ , the morphism $$\begin{align*} &F^{\prime}([Y\rightarrowtail U \rightarrowtail W]_{G/H})\rightarrow F^{\prime}([U \rightarrowtail W]_{G/H})\end{align*}$$ is an equivalence. This reinterpretation of fibrewise inerts being sent to cocartesian morphisms is again by Remark A.15 .

We may now deduce the desired equivalence:

Let |$\underline{{\mathcal{C}}}$| be a |$G$| –category with finite indexed products. There is a canonical equivalence |$\textrm{CMon}_{G}(\underline{{\mathcal{C}}})\simeq \textrm{CAlg}_{G}(\underline{{\mathcal{C}}}^{\underline{\times }})$|⁠ .

Immediate combination of Lemma A.20 and Lemma A.22 , using also that |$\textrm{CAlg}_{G}(\underline{{\mathcal{C}}}^{\underline{\times }})=\textrm{Fun}_{/\underline{\textrm{Fin}}_{*}}^{\textrm{int}}(\underline{\textrm{Fin}}_{*},\underline{{\mathcal{C}}}^{\underline{\times }})$| by definition.

The author was supported by the Max Planck Institute for Mathematics in Bonn, Germany, where this work was conceived and carried out.

We thank J.D. Quigley and Eva Belmont for posing the question as to what an “equivariant group–completion theorem” should be, which directly led us to writing this note. We also thank Maxime Ramzi for going through a draft and for helpful suggestions. Finally, we are also grateful to the anonymous referee whose patient comments led to a minor correction, many expositional improvements, as well as the writing of the appendix.

Communicated by Prof. Andrew Blumberg

Barwick , C. , Dotto , E. , Glasman , S. , Nardin , D. , and Shah , J. “ Parametrized higher category theory and higher algebra: a general introduction .” Preprint, arXiv:1608.03654 .

Barwick , C. “ Spectral Mackey functors and equivariant algebraic K-theory (I) .” Adv. Math. 304 ( 2017 ): 646 – 727 . https://doi.org/10.1016/j.aim.2016.08.043 .

Google Scholar

Barwick , C. , S. Glasman , and J. Shah “ Spectral Mackey functors and equivariant algebraic K-theory, II .” Tunis. J. Math. 2 , no. 1 ( 2020 ): 97 – 146 . https://doi.org/10.2140/tunis.2020.2.97 .

Calmés , B. , Dotto , E. , Harpaz , Y. , Hebestreit , F. , Land , M. , Moi , K. , Nardin , D. , Nikolaus , T. , and Steimle , W. “ Hermitian K-theory for stable |$\infty $| -categories II: cobordism categories and additivity .” Preprint, arXiv:2009.07224 .

Chu , H. , and R. Haugseng “ Homotopy-coherent algebra via Segal conditions .” Adv. Math. 385 ( 2021 ): 107733 . https://doi.org/10.1016/j.aim.2021.107733 .

Chu , H. , and R. Haugseng “ Free algebras through Day convolution .” Algebr. Geom. Topol. 22 , no. 7 ( 2022 ): 3401 – 58 . https://doi.org/10.2140/agt.2022.22.3401 .

Clausen , D. , Mathew , A. , Naumann , N. , and Noel , J. “ Descent and vanishing in chromatic algebraic K-theory via group actions .” Ann. Sci. Éc. Norm. Supér. (4) . Preprint, arXiv:2011.08233 .

Galatius , S. , and Randal-Williams O. “ Stable moduli spaces of high-dimensional manifolds .” Acta Math. 212 ( 2014 ): 257 – 377 . https://doi.org/10.1007/s11511-014-0112-7 .

Galatius , S. , and O. Randal-Williams “ Homological stability for moduli spaces of high dimensional manifolds. II .” Ann. Math. (2) 186 ( 2017 ): 127 – 204 .

Galatius , S. , and G. Szűcs “ The equivariant cobordism category .” J. Topol. 14 , no. 1 ( 2021 ): 215 – 57 . https://doi.org/10.1112/topo.12181 .

Gepner , D. , M. Groth , and T. Nikolaus “ Universality of multiplicative infinite loop space machines .” Algebr. Geom. Topol. 15 ( 2015 ): 3107 – 53 . https://doi.org/10.2140/agt.2015.15.3107 .

Greenlees , J. P. C. , and J. P. May “ Localization and completion theorems for MU–module spectra .” Ann. Math. (2) 146 ( 1997 ): 509 – 44 .

Hebestreit , F. , and F. Wagner Lecture Notes for Algebraic and Hermitian K-Theory . Available on the author’swebpage .

Hill , M. , and Hopkins , M. “ Equivariant multiplicative closure .” Preprint, arXiv:1303.4479 .

Hill , M. , M. Hopkins , and D. Ravenel “ On the non-existence of elements of Kervaire invariant one .” Ann. Math. (2) 184 ( 2016 ): 1 – 262 .

Hilman , K . “ Norms and periodicities in genuine equivariant hermitian K–theory .” PhD thesis , University of Copenhagen , available on the author’swebpage .

Lurie , J. Higher Algebra . Available on the author’swebpage .

Mathew , A. , N. Naumann , and J. Noel “ Nilpotence and descent in equivariant stable homotopy theory .” Adv. Math. 305 ( 2017 ): 994 – 1084 . https://doi.org/10.1016/j.aim.2016.09.027 .

McDuff , D. , and G. Segal “ Homology fibrations and the ‘group-completion’ theorem .” Invent. Math. 31 ( 1976 ): 279 – 84 . https://doi.org/10.1007/BF01403148 .

Nardin , D. , “ Parametrized higher category theory and higher algebra: ExposéIV–Stability with respect to an orbital |$\infty $| -category .” Preprint, arXiv:1608.07704 .

Nardin , D. “ Stability and distributivity over orbital |$\infty $| - categories .” PhD thesis , MIT .

Nardin , D. , and Shah , J. “ Parametrized and equivariant higher algebra .” Preprint, arXiv:2203.00072 .

Nikolaus , T. The Group–Completion Theorem via Localizations of Ring Spectra . Available on author’swebpage .

Randal-Williams , O. “ ‘Group–completion’, local coefficient systems, and perfection .” Q. J. Math. (Quillen Memorial Issue) 64 , no. 3 ( 2013 ): 795 – 803 . https://doi.org/10.1093/qmath/hat024 .

Quigley , J.D. , and Shah , J. “ On the parametrized Tate construction .” Preprint, arXiv:2110.07707 .

Schwede , S. Lecture Notes on Equivariant Stable Homotopy Theory . Available on author’swebpage .

Shah , J. “ Parametrized higher category theory .” Algebr. Geom. Topol. 23 , no. 2 ( 2023 ): 509 – 644 . https://doi.org/10.2140/agt.2023.23.509 .

Shah , J. “ Parametrized higher category theory II: universal constructions .” Preprint, arXiv:2109.11954 .

Email alerts

Citing articles via.

• Recommend to your Library

Affiliations

• Online ISSN 1687-0247
• Print ISSN 1073-7928
• Copyright © 2024 Oxford University Press
• About Oxford Academic
• Publish journals with us
• University press partners
• What we publish
• New features  
• Open access
• Institutional account management
• Rights and permissions
• Get help with access
• Accessibility
• Advertising
• Media enquiries
• Oxford University Press
• Oxford Languages
• University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

• Copyright © 2024 Oxford University Press
• Cookie settings
• Cookie policy
• Privacy policy
• Legal notice

This Feature Is Available To Subscribers Only

Sign In or Create an Account

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.