what is the probability assignment

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.6: Basic Concepts of Probability

• Last updated
• Save as PDF
• Page ID 129597

Learning Objectives

After completing this section, you should be able to:

• Define probability including impossible and certain events.
• Calculate basic theoretical probabilities.
• Calculate basic empirical probabilities.
• Distinguish among theoretical, empirical, and subjective probability.
• Calculate the probability of the complement of an event.

It all comes down to this. The game of Monopoly that started hours ago is in the home stretch. Your sister has the dice, and if she rolls a 4, 5, or 7 she’ll land on one of your best spaces and the game will be over. How likely is it that the game will end on the next turn? Is it more likely than not? How can we measure that likelihood? This section addresses this question by introducing a way to measure uncertainty.

Introducing Probability

Uncertainty is, almost by definition, a nebulous concept. In order to put enough constraints on it that we can mathematically study it, we will focus on uncertainty strictly in the context of experiments. Recall that experiments are processes whose outcomes are unknown; the sample space for the experiment is the collection of all those possible outcomes. When we want to talk about the likelihood of particular outcomes, we sometimes group outcomes together; for example, in the Monopoly example at the beginning of this section, we were interested in the roll of 2 dice that might fall as a 4, 5, or 7. A grouping of outcomes that we’re interested in is called an event . In other words, an event is a subset of the sample space of an experiment; it often consists of the outcomes of interest to the experimenter.

Once we have defined the event that interests us, we can try to assess the likelihood of that event. We do that by assigning a number to each event ( E E ) called the probability of that event ( P ( E ) P ( E ) ). The probability of an event is a number between 0 and 1 (inclusive). If the probability of an event is 0, then the event is impossible. On the other hand, an event with probability 1 is certain to occur. In general, the higher the probability of an event, the more likely it is that the event will occur.

Example 7.16

Determining certain and impossible events.

Consider an experiment that consists of rolling a single standard 6-sided die (with faces numbered 1-6). Decide if these probabilities are equal to zero, equal to one, or somewhere in between.

• P ( roll a 4 ) P ( roll a 4 )
• P ( roll a 7 ) P ( roll a 7 )
• P ( roll a positive number ) P ( roll a positive number )
• P ( roll a 1 3 ) P ( roll a 1 3 )
• P ( roll an even number ) P ( roll an even number )
• P ( roll a single-digit number ) P ( roll a single-digit number )

Let's start by identifying the sample space. For one roll of this die, the possible outcomes are {1, 2, 3, 4, 5,6}. We can use that to assess these probabilities:

• We see that 4 is in the sample space, so it’s possible that it will be the outcome. It’s not certain to be the outcome, though. So, 0 < P ( roll a 4 ) < 1 0 < P ( roll a 4 ) < 1 .
• Notice that 7 is not in the sample space. So, P ( roll a 7 ) = 0 P ( roll a 7 ) = 0 .
• Every outcome in the sample space is a positive number, so this event is certain. Thus, P ( roll a positive number ) = 1 P ( roll a positive number ) = 1 .
• Since 1 3 1 3 is not in the sample space, P ( roll a 1 3 ) = 0 P ( roll a 1 3 ) = 0 .
• Some outcomes in the sample space are even numbers (2, 4, and 6), but the others aren’t. So, 0 < P ( roll an even number ) < 1 0 < P ( roll an even number ) < 1 .
• Every outcome in the sample space is a single-digit number, so P ( roll a single-digit number ) = 1 P ( roll a single-digit number ) = 1 .

Your Turn 7.16

Three ways to assign probabilities.

The probabilities of events that are certain or impossible are easy to assign; they’re just 1 or 0, respectively. What do we do about those in-between cases, for events that might or might not occur? There are three methods to assign probabilities that we can choose from. We’ll discuss them here, in order of reliability.

Method 1: Theoretical Probability

The theoretical method gives the most reliable results, but it cannot always be used. If the sample space of an experiment consists of equally likely outcomes, then the theoretical probability of an event is defined to be the ratio of the number of outcomes in the event to the number of outcomes in the sample space.

For an experiment whose sample space S S consists of equally likely outcomes, the theoretical probability of the event E E is the ratio

P ( E ) = n ( E ) n ( S ) , P ( E ) = n ( E ) n ( S ) ,

where n ( E ) n ( E ) and n ( S ) n ( S ) denote the number of outcomes in the event and in the sample space, respectively.

Example 7.17

Computing theoretical probabilities.

Recall that a standard deck of cards consists of 52 unique cards which are labeled with a rank (the whole numbers from 2 to 10, plus J, Q, K, and A) and a suit ( ♣ ♣ , ♢ ♢ , ♡ ♡ , or ♠ ♠ ). A standard deck is thoroughly shuffled, and you draw one card at random (so every card has an equal chance of being drawn). Find the theoretical probability of each of these events:

• The card is 10 ♠ 10 ♠ .
• The card is a ♡ ♡ .
• The card is a king (K).

There are 52 cards in the deck, so the sample space for each of these experiments has 52 elements. That will be the denominator for each of our probabilities.

• There is only one 10 ♠ 10 ♠ in the deck, so this event only has one outcome in it. Thus, P ( 10 ♠ ) = 1 52 P ( 10 ♠ ) = 1 52 .
• There are 13 ♡ s ♡ s in the deck, so P ( ♡ ) = 13 52 = 1 4 P ( ♡ ) = 13 52 = 1 4 .
• There are 4 cards of each rank in the deck, so P ( K ) = 4 52 = 1 13 P ( K ) = 4 52 = 1 13 .

Your Turn 7.17

It is critical that you make sure that every outcome in a sample space is equally likely before you compute theoretical probabilities!

Example 7.18

Using tables to find theoretical probabilities.

In the Basic Concepts of Probability, we were considering a Monopoly game where, if your sister rolled a sum of 4, 5, or 7 with 2 standard dice, you would win the game. What is the probability of this event? Use tables to determine your answer.

We should think of this experiment as occurring in two stages: (1) one die roll, then (2) another die roll. Even though these two stages will usually occur simultaneously in practice, since they’re independent, it’s okay to treat them separately.

Step 1: Since we have two independent stages, let’s create a table (Figure 7.27), which is probably the most efficient method for determining the sample space.

Now, each of the 36 ordered pairs in the table represent an equally likely outcome.

Step 2: To make our analysis easier, let’s replace each ordered pair with the sum (Figure 7.28).

Step 3: Since the event we’re interested in is the one consisting of rolls of 4, 5, or 7. Let’s shade those in (Figure 7.29).

Our event contains 13 outcomes, so the probability that your sister rolls a losing number is 13 36 13 36 .

Your Turn 7.18

Example 7.19, using tree diagrams to compute theoretical probability.

If you flip a fair coin 3 times, what is the probability of each event? Use a tree diagram to determine your answer

• You flip exactly 2 heads.
• You flip 2 consecutive heads at some point in the 3 flips.
• All 3 flips show the same result.

Let’s build a tree to identify the sample space (Figure 7.30).

The sample space is {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}, which has 8 elements.

• Flipping exactly 2 heads occurs three times (HHT, HTH, THH), so the probability is 3 8 3 8 .
• Flipping 2 consecutive heads at some point in the experiment happens 3 times: HHH, HHT, THH. So, the probability is 3 8 3 8 .
• There are 2 outcomes that all show the same result: HHH and TTT. So, the probability is 2 8 = 1 4 2 8 = 1 4 .

Your Turn 7.19

People in mathematics, gerolamo cardano.

The first known text that provided a systematic approach to probabilities was written in 1564 by Gerolamo Cardano (1501–1576). Cardano was a physician whose illegitimate birth closed many doors that would have otherwise been open to someone with a medical degree in 16th-century Italy. As a result, Cardano often turned to gambling to help ends meet. He was a remarkable mathematician, and he used his knowledge to gain an edge when playing at cards or dice. His 1564 work, titled Liber de ludo aleae (which translates as Book on Games of Chance ), summarized everything he knew about probability. Of course, if that book fell into the hands of those he played against, his advantage would disappear. That’s why he never allowed it to be published in his lifetime (it was eventually published in 1663). Cardano made other contributions to mathematics; he was the first person to publish the third degree analogue of the Quadratic Formula (though he didn’t discover it himself), and he popularized the use of negative numbers.

Method 2: Empirical Probability

Theoretical probabilities are precise, but they can’t be found in every situation. If the outcomes in the sample space are not equally likely, then we’re out of luck. Suppose you’re watching a baseball game, and your favorite player is about to step up to the plate. What is the probability that he will get a hit?

In this case, the sample space is {hit, not a hit}. That doesn’t mean that the probability of a hit is 1 2 1 2 , since those outcomes aren’t equally likely. The theoretical method simply can’t be used in this situation. Instead, we might look at the player’s statistics up to this point in the season, and see that he has 122 hits in 531 opportunities. So, we might think that the probability of a hit in the next plate appearance would be about 122 531 ≈ 0.23 122 531 ≈ 0.23 . When we use the outcomes of previous replications of an experiment to assign a probability to the next replication, we’re defining an empirical probability . Empirical probability is assigned using the outcomes of previous replications of an experiment by finding the ratio of the number of times in the previous replications the event occurred to the total number of previous replications.

Empirical probabilities aren’t exact, but when the number of previous replications is large, we expect them to be close. Also, if the previous runs of the experiment are not conducted under the exact set of circumstances as the one we’re interested in, the empirical probability is less reliable. For instance, in the case of our favorite baseball player, we might try to get a better estimate of the probability of a hit by looking only at his history against left- or right-handed pitchers (depending on the handedness of the pitcher he’s about to face).

Probability and Statistics

One of the broad uses of statistics is called statistical inference, where statisticians use collected data to make a guess (or inference) about the population the data were collected from. Nearly every tool that statisticians use for inference is based on probability. Not only is the method we just described for finding empirical probabilities one type of statistical inference, but some more advanced techniques in the field will give us an idea of how close that empirical probability might be to the actual probability!

Example 7.20

Finding empirical probabilities.

Assign an empirical probability to the following events:

• Jose is on the basketball court practicing his shots from the free throw line. He made 47 out of his last 80 attempts. What is the probability he makes his next shot?
• Amy is about to begin her morning commute. Over her last 60 commutes, she arrived at work 12 times in under half an hour. What is the probability that she arrives at work in 30 minutes or less?
• Felix is playing Yahtzee with his sister. Felix won 14 of the last 20 games he played against her. How likely is he to win this game?
• Since Jose made 47 out of his last 80 attempts, assign this event an empirical probability of 47 80 ≈ 59 % 47 80 ≈ 59 % .
• Amy completed the commute in under 30 minutes in 12 of the last 60 commutes, so we can estimate her probability of making it in under 30 minutes this time at 12 60 = 20 % 12 60 = 20 % .
• Since Felix has won 14 of the last 20 games, assign a probability for a win this time of 14 20 = 70 % 14 20 = 70 % .

Your Turn 7.20

Work it out, buffon’s needle.

A famous early question about probability (posed by Georges-Louis Leclerc, Comte de Buffon in the 18th century) had to do with the probability that a needle dropped on a floor finished with wooden slats would lay across one of the seams. If the distance between the slats is exactly the same length as the needle, then it can be shown using calculus that the probability that the needle crosses a seam is 2 π 2 π . Using toothpicks or matchsticks (or other uniformly long and narrow objects), assign an empirical probability to this experiment by drawing parallel lines on a large sheet of paper where the distance between the lines is equal to the length of your dropping object, then repeatedly dropping the objects and noting whether the object touches one of the lines. Once you have your empirical probability, take its reciprocal and multiply by 2. Is the result close to π π ?

Method 3: Subjective Probability

In cases where theoretical probability can’t be used and we don’t have prior experience to inform an empirical probability, we’re left with one option: using our instincts to guess at a subjective probability . A subjective probability is an assignment of a probability to an event using only one’s instincts.

Subjective probabilities are used in cases where an experiment can only be run once, or it hasn’t been run before. Because subjective probabilities may vary widely from person to person and they’re not based on any mathematical theory, we won’t give any examples. However, it’s important that we be able to identify a subjective probability when we see it; they will in general be far less accurate than empirical or theoretical probabilities.

Example 7.21

Distinguishing among theoretical, empirical, and subjective probabilities.

Classify each of the following probabilities as theoretical, empirical, or subjective.

• An eccentric billionaire is testing a brand new rocket system. He says there is a 15% chance of failure.
• With 4 seconds to go in a close basketball playoff game, the home team need 3 points to tie up the game and send it to overtime. A TV commentator says that team captain should take the final 3-point shot, because he has a 38% chance of making it (greater than every other player on the team).
• Felix is losing his Yahtzee game against his sister. He has one more chance to roll 2 dice; he’ll win the game if they both come up 4. The probability of this is about 2.8%.
• This experiment has never been run before, so the given probability is subjective.
• Presumably, the commentator has access to each player’s performance statistics over the entire season. So, the given probability is likely empirical.
• Rolling 2 dice results in a sample space with equally likely outcomes. This probability is theoretical. (We’ll learn how to calculate that probability later in this chapter.)

Your Turn 7.21

Benford’s law.

In 1938, Frank Benford published a paper (“The law of anomalous numbers,” in Proceedings of the American Philosophical Society ) with a surprising result about probabilities. If you have a list of numbers that spans at least a couple of orders of magnitude (meaning that if you divide the largest by the smallest, the result is at least 100), then the digits 1–9 are not equally likely to appear as the first digit of those numbers, as you might expect. Benford arrived at this conclusion using empirical probabilities; he found that 1 was about 6 times as likely to be the initial digit as 9 was!

New Probabilities from Old: Complements

One of the goals of the rest of this chapter is learning how to break down complicated probability calculations into easier probability calculations. We’ll look at the first of the tools we can use to accomplish this goal in this section; the rest will come later.

Given an event E E , the complement of E E (denoted E ′ E ′ ) is the collection of all of the outcomes that are not in E E . (This is language that is taken from set theory, which you can learn more about elsewhere in this text.) Since every outcome in the sample space either is or is not in E E , it follows that n ( E ) + n ( E ′ ) = n ( S ) n ( E ) + n ( E ′ ) = n ( S ) . So, if the outcomes in S S are equally likely, we can compute theoretical probabilities P ( E ) = n ( E ) n ( S ) P ( E ) = n ( E ) n ( S ) and P ( E ′ ) = n ( E ′ ) n ( S ) P ( E ′ ) = n ( E ′ ) n ( S ) . Then, adding these last two equations, we get

P ( E ) + P ( E ′ ) = n ( E ) n ( S ) + n ( E ′ ) n ( S ) = n ( E ) + n ( E ′ ) n ( S ) = n ( S ) n ( S ) = 1 P ( E ) + P ( E ′ ) = n ( E ) n ( S ) + n ( E ′ ) n ( S ) = n ( E ) + n ( E ′ ) n ( S ) = n ( S ) n ( S ) = 1

Thus, if we subtract P ( E ′ ) P ( E ′ ) from both sides, we can conclude that P ( E ) = 1 − P ( E ′ ) P ( E ) = 1 − P ( E ′ ) . Though we performed this calculation under the assumption that the outcomes in S S are all equally likely, the last equation is true in every situation.

P ( E ) = 1 − P ( E ′ ) P ( E ) = 1 − P ( E ′ )

How is this helpful? Sometimes it is easier to compute the probability that an event won’t happen than it is to compute the probability that it will . To apply this principle, it’s helpful to review some tricks for dealing with inequalities. If an event is defined in terms of an inequality, the complement will be defined in terms of the opposite inequality: Both the direction and the inclusivity will be reversed, as shown in the table below.

Example 7.22

Using the formula for complements to compute probabilities.

• If you roll a standard 6-sided die, what is the probability that the result will be a number greater than one?
• If you roll two standard 6-sided dice, what is the probability that the sum will be 10 or less?
• If you flip a fair coin 3 times, what is the probability that at least one flip will come up tails?
• Here, the sample space is {1, 2, 3, 4, 5, 6}. It’s easy enough to see that the probability in question is 5 6 5 6 , because there are 5 outcomes that fall into the event “roll a number greater than 1.” Let’s also apply our new formula to find that probability. Since E E is defined using the inequality roll > 1 roll > 1 , then E ′ E ′ is defined using roll ≤ 1 roll ≤ 1 . Since there’s only one outcome (1) in E ′ E ′ , we have P ( E ′ ) = 1 6 P ( E ′ ) = 1 6 . Thus, P ( E ) = 1 − P ( E ′ ) = 5 6 P ( E ) = 1 − P ( E ′ ) = 5 6 .

Here, the event E E is defined by the inequality sum ≤ 10 sum ≤ 10 . Thus, E ′ E ′ is defined by sum > 10 sum > 10 . There are three outcomes in E ′ E ′ : two 11s and one 12. Thus, P ( E ) = 1 − P ( E ′ ) = 1 − 3 36 = 11 12 P ( E ) = 1 − P ( E ′ ) = 1 − 3 36 = 11 12 .

• In Example 7.15, we found the sample space for this experiment consisted of these equally likely outcomes: {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}. Our event E E is defined by T ≥ 1 T ≥ 1 , so E ′ E ′ is defined by T < 1 T < 1 . The only outcome in E ′ E ′ is the first one on the list, where zero tails are flipped. So, P ( E ) = 1 − P ( E ′ ) = 1 − 1 8 = 7 8 P ( E ) = 1 − P ( E ′ ) = 1 − 1 8 = 7 8 .

Your Turn 7.22

Check your understanding, section 7.5 exercises.

For the following exercises, use the following table of the top 15 players by number of plate appearances (PA) in the 2019 Major League Baseball season to assign empirical probabilities to the given events. A plate appearance is a batter’s opportunity to try to get a hit. The other columns are runs scored (R), hits (H), doubles (2B), triples (3B), home runs (HR), walks (BB), and strike outs (SO).

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.1: Sample Spaces, Events, and Their Probabilities

• Last updated
• Save as PDF
• Page ID 530

Learning Objectives

• To learn the concept of the sample space associated with a random experiment.
• To learn the concept of an event associated with a random experiment.
• To learn the concept of the probability of an event.

Sample Spaces and Events

Rolling an ordinary six-sided die is a familiar example of a random experiment , an action for which all possible outcomes can be listed, but for which the actual outcome on any given trial of the experiment cannot be predicted with certainty. In such a situation we wish to assign to each outcome, such as rolling a two, a number, called the probability of the outcome, that indicates how likely it is that the outcome will occur. Similarly, we would like to assign a probability to any event , or collection of outcomes, such as rolling an even number, which indicates how likely it is that the event will occur if the experiment is performed. This section provides a framework for discussing probability problems, using the terms just mentioned.

Definition: random experiment

A random experiment is a mechanism that produces a definite outcome that cannot be predicted with certainty. The sample space associated with a random experiment is the set of all possible outcomes. An event is a subset of the sample space.

Definition: Element and Occurrence

An event \(E\) is said to occur on a particular trial of the experiment if the outcome observed is an element of the set \(E\).

Example \(\PageIndex{1}\): Sample Space for a single coin

Construct a sample space for the experiment that consists of tossing a single coin.

The outcomes could be labeled \(h\) for heads and \(t\) for tails. Then the sample space is the set: \(S = \{h,t\}\)

Example \(\PageIndex{2}\): Sample Space for a single die

Construct a sample space for the experiment that consists of rolling a single die. Find the events that correspond to the phrases “an even number is rolled” and “a number greater than two is rolled.”

The outcomes could be labeled according to the number of dots on the top face of the die. Then the sample space is the set \(S = \{1,2,3,4,5,6\}\)

The outcomes that are even are \(2, 4,\; \; \text{and}\; \; 6\), so the event that corresponds to the phrase “an even number is rolled” is the set \(\{2,4,6\}\), which it is natural to denote by the letter \(E\). We write \(E=\{2,4,6\}\).

Similarly the event that corresponds to the phrase “a number greater than two is rolled” is the set \(T=\{3,4,5,6\}\), which we have denoted \(T\).

A graphical representation of a sample space and events is a Venn diagram , as shown in Figure \(\PageIndex{1}\). In general the sample space \(S\) is represented by a rectangle, outcomes by points within the rectangle, and events by ovals that enclose the outcomes that compose them.

Example \(\PageIndex{3}\): Sample Spaces for two coines

A random experiment consists of tossing two coins.

• Construct a sample space for the situation that the coins are indistinguishable, such as two brand new pennies.
• Construct a sample space for the situation that the coins are distinguishable, such as one a penny and the other a nickel.
• After the coins are tossed one sees either two heads, which could be labeled \(2h\), two tails, which could be labeled \(2t\), or coins that differ, which could be labeled \(d\) Thus a sample space is \(S=\{2h, 2t, d\}\).
• Since we can tell the coins apart, there are now two ways for the coins to differ: the penny heads and the nickel tails, or the penny tails and the nickel heads. We can label each outcome as a pair of letters, the first of which indicates how the penny landed and the second of which indicates how the nickel landed. A sample space is then \(S' = \{hh, ht, th, tt\}\).

A device that can be helpful in identifying all possible outcomes of a random experiment, particularly one that can be viewed as proceeding in stages, is what is called a tree diagram . It is described in the following example.

Example \(\PageIndex{4}\): Tree diagram

Construct a sample space that describes all three-child families according to the genders of the children with respect to birth order.

Two of the outcomes are “two boys then a girl,” which we might denote \(bbg\), and “a girl then two boys,” which we would denote \(gbb\).

Clearly there are many outcomes, and when we try to list all of them it could be difficult to be sure that we have found them all unless we proceed systematically. The tree diagram shown in Figure \(\PageIndex{2}\), gives a systematic approach.

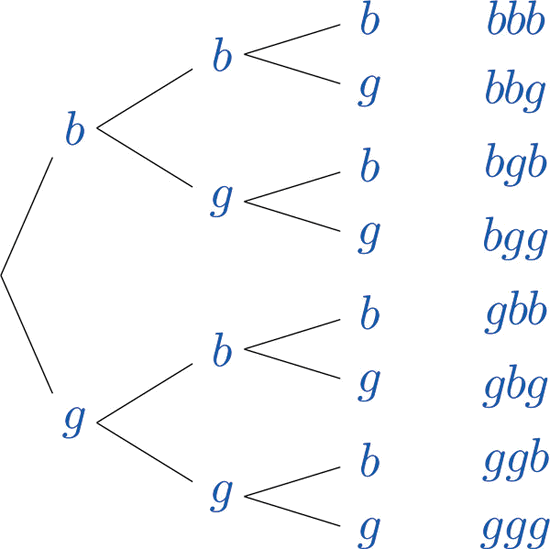
The diagram was constructed as follows. There are two possibilities for the first child, boy or girl, so we draw two line segments coming out of a starting point, one ending in a \(b\) for “boy” and the other ending in a \(g\) for “girl.” For each of these two possibilities for the first child there are two possibilities for the second child, “boy” or “girl,” so from each of the \(b\) and \(g\) we draw two line segments, one segment ending in a \(b\) and one in a \(g\). For each of the four ending points now in the diagram there are two possibilities for the third child, so we repeat the process once more.

The line segments are called branches of the tree. The right ending point of each branch is called a node . The nodes on the extreme right are the final nodes ; to each one there corresponds an outcome, as shown in the figure.

From the tree it is easy to read off the eight outcomes of the experiment, so the sample space is, reading from the top to the bottom of the final nodes in the tree,

\[S=\{bbb,\; bbg,\; bgb,\; bgg,\; gbb,\; gbg,\; ggb,\; ggg\} \nonumber \]

Probability

Definition: probability.

The probability of an outcome \(e\) in a sample space \(S\) is a number \(P\) between \(1\) and \(0\) that measures the likelihood that \(e\) will occur on a single trial of the corresponding random experiment. The value \(P=0\) corresponds to the outcome \(e\) being impossible and the value \(P=1\) corresponds to the outcome \(e\) being certain.

Definition: probability of an event

The probability of an event \(A\) is the sum of the probabilities of the individual outcomes of which it is composed. It is denoted \(P(A)\).

The following formula expresses the content of the definition of the probability of an event:

If an event \(E\) is \(E=\{e_1,e_2,...,e_k\}\), then

\[P(E)=P(e_1)+P(e_2)+...+P(e_k) \nonumber \]

The following figure expresses the content of the definition of the probability of an event:

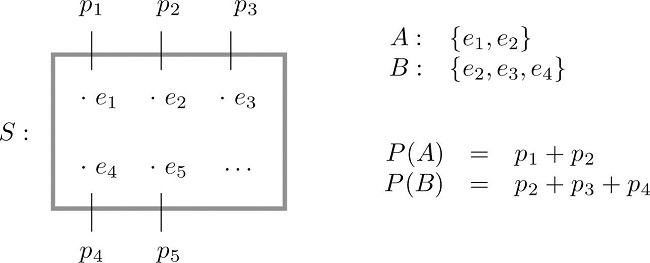
Since the whole sample space \(S\) is an event that is certain to occur, the sum of the probabilities of all the outcomes must be the number \(1\).

In ordinary language probabilities are frequently expressed as percentages. For example, we would say that there is a \(70\%\) chance of rain tomorrow, meaning that the probability of rain is \(0.70\). We will use this practice here, but in all the computational formulas that follow we will use the form \(0.70\) and not \(70\%\).

Example \(\PageIndex{5}\)

A coin is called “balanced” or “fair” if each side is equally likely to land up. Assign a probability to each outcome in the sample space for the experiment that consists of tossing a single fair coin.

With the outcomes labeled \(h\) for heads and \(t\) for tails, the sample space is the set

\[S=\{h,t\} \nonumber \]

Since the outcomes have the same probabilities, which must add up to \(1\), each outcome is assigned probability \(1/2\).

Example \(\PageIndex{6}\)

A die is called “balanced” or “fair” if each side is equally likely to land on top. Assign a probability to each outcome in the sample space for the experiment that consists of tossing a single fair die. Find the probabilities of the events \(E\): “an even number is rolled” and \(T\): “a number greater than two is rolled.”

With outcomes labeled according to the number of dots on the top face of the die, the sample space is the set

\[S=\{1,2,3,4,5,6\} \nonumber \]

Since there are six equally likely outcomes, which must add up to \(1\), each is assigned probability \(1/6\).

Since \(E = \{2,4,6\}\),

\[P(E) = \dfrac{1}{6} + \dfrac{1}{6} + \dfrac{1}{6} = \dfrac{3}{6} = \dfrac{1}{2} \nonumber \]

Since \(T = \{3,4,5,6\}\),

\[P(T) = \dfrac{4}{6} = \dfrac{2}{3} \nonumber \]

Example \(\PageIndex{7}\)

Two fair coins are tossed. Find the probability that the coins match, i.e., either both land heads or both land tails.

In Example \(\PageIndex{3}\) we constructed the sample space \(S=\{2h,2t,d\}\) for the situation in which the coins are identical and the sample space \(S′=\{hh,ht,th,tt\}\) for the situation in which the two coins can be told apart.

The theory of probability does not tell us how to assign probabilities to the outcomes, only what to do with them once they are assigned. Specifically, using sample space \(S\), matching coins is the event \(M=\{2h, 2t\}\) which has probability \(P(2h)+P(2t)\). Using sample space \(S'\), matching coins is the event \(M'=\{hh, tt\}\), which has probability \(P(hh)+P(tt)\). In the physical world it should make no difference whether the coins are identical or not, and so we would like to assign probabilities to the outcomes so that the numbers \(P(M)\) and \(P(M')\) are the same and best match what we observe when actual physical experiments are performed with coins that seem to be fair. Actual experience suggests that the outcomes in S' are equally likely, so we assign to each probability \(\frac{1}{4}\), and then...

\[P(M') = P(hh) + P(tt) = \frac{1}{4} + \frac{1}{4} = \frac{1}{2} \nonumber \]

Similarly, from experience appropriate choices for the outcomes in \(S\) are:

\[P(2h) = \frac{1}{4} \nonumber \]

\[P(2t) = \frac{1}{4} \nonumber \]

\[P(d) = \frac{1}{2} \nonumber \]

The previous three examples illustrate how probabilities can be computed simply by counting when the sample space consists of a finite number of equally likely outcomes. In some situations the individual outcomes of any sample space that represents the experiment are unavoidably unequally likely, in which case probabilities cannot be computed merely by counting, but the computational formula given in the definition of the probability of an event must be used.

Example \(\PageIndex{8}\)

The breakdown of the student body in a local high school according to race and ethnicity is \(51\%\) white, \(27\%\) black, \(11\%\) Hispanic, \(6\%\) Asian, and \(5\%\) for all others. A student is randomly selected from this high school. (To select “randomly” means that every student has the same chance of being selected.) Find the probabilities of the following events:

• \(B\): the student is black,
• \(M\): the student is minority (that is, not white),
• \(N\): the student is not black.

The experiment is the action of randomly selecting a student from the student population of the high school. An obvious sample space is \(S=\{w,b,h,a,o\}\). Since \(51\%\) of the students are white and all students have the same chance of being selected, \(P(w)=0.51\), and similarly for the other outcomes. This information is summarized in the following table:

\[\begin{array}{l|cccc}Outcome & w & b & h & a & o \\ Probability & 0.51 & 0.27 & 0.11 & 0.06 & 0.05\end{array} \nonumber \]

• Since \(B=\{b\},\; \; P(B)=P(b)=0.27\)
• Since \(M=\{b,h,a,o\},\; \; P(M)=P(b)+P(h)+P(a)+P(o)=0.27+0.11+0.06+0.05=0.49\)
• Since \(N=\{w,h,a,o\},\; \; P(N)=P(w)+P(h)+P(a)+P(o)=0.51+0.11+0.06+0.05=0.73\)

Example \(\PageIndex{9}\)

The student body in the high school considered in the last example may be broken down into ten categories as follows: \(25\%\) white male, \(26\%\) white female, \(12\%\) black male, \(15\%\) black female, 6% Hispanic male, \(5\%\) Hispanic female, \(3\%\) Asian male, \(3\%\) Asian female, \(1\%\) male of other minorities combined, and \(4\%\) female of other minorities combined. A student is randomly selected from this high school. Find the probabilities of the following events:

• \(B\): the student is black
• \(MF\): the student is a non-white female
• \(FN\): the student is female and is not black

Now the sample space is \(S=\{wm, bm, hm, am, om, wf, bf, hf, af, of\}\). The information given in the example can be summarized in the following table, called a two-way contingency table:

• Since \(B=\{bm, bf\},\; \; P(B)=P(bm)+P(bf)=0.12+0.15=0.27\)
• Since \(MF=\{bf, hf, af, of\},\; \; P(M)=P(bf)+P(hf)+P(af)+P(of)=0.15+0.05+0.03+0.04=0.27\)
• Since \(FN=\{wf, hf, af, of\},\; \; P(FN)=P(wf)+P(hf)+P(af)+P(of)=0.26+0.05+0.03+0.04=0.38​​​​​​\)

Key Takeaway

• The sample space of a random experiment is the collection of all possible outcomes.
• An event associated with a random experiment is a subset of the sample space.
• The probability of any outcome is a number between \(0\) and \(1\). The probabilities of all the outcomes add up to \(1\).
• The probability of any event \(A\) is the sum of the probabilities of the outcomes in \(A\).

• Math Article

Probability

Probability  means possibility. It is a branch of mathematics that deals with the occurrence of a random event. The value is expressed from zero to one. Probability has been introduced in Maths to predict how likely events are to happen. The meaning of probability is basically the extent to which something is likely to happen. This is the basic probability theory, which is also used in the  probability distribution , where you will learn the possibility of outcomes for a random experiment. To find the probability of a single event to occur, first, we should know the total number of possible outcomes.

Learn More here: Study Mathematics

Probability Definition in Math

Probability is a measure of the likelihood of an event to occur. Many events cannot be predicted with total certainty. We can predict only the chance of an event to occur i.e., how likely they are going to happen, using it. Probability can range from 0 to 1, where 0 means the event to be an impossible one and 1 indicates a certain event. Probability for Class 10 is an important topic for the students which explains all the basic concepts of this topic. The probability of all the events in a sample space adds up to 1.

For example , when we toss a coin, either we get Head OR Tail, only two possible outcomes are possible (H, T). But when two coins are tossed then there will be four possible outcomes,  i.e {(H, H), (H, T), (T, H),  (T, T)}.

Download this lesson as PDF: – Download PDF Here

Formula for Probability

The probability formula is defined as the possibility of an event to happen is equal to the ratio of the number of favourable outcomes and the total number of outcomes.

Sometimes students get mistaken for “favourable outcome” with “desirable outcome”. This is the basic formula. But there are some more formulas for different situations or events.

Solved Examples

1) There are 6 pillows in a bed, 3 are red, 2 are yellow and 1 is blue. What is the probability of picking a yellow pillow?

Ans: The probability is equal to the number of yellow pillows in the bed divided by the total number of pillows, i.e. 2/6 = 1/3.

2) There is a container full of coloured bottles, red, blue, green and orange. Some of the bottles are picked out and displaced. Sumit did this 1000 times and got the following results:

• No. of blue bottles picked out: 300
• No. of red bottles: 200
• No. of green bottles: 450
• No. of orange bottles: 50

a) What is the probability that Sumit will pick a green bottle?

Ans: For every 1000 bottles picked out, 450 are green.

Therefore, P(green) = 450/1000 = 0.45

b) If there are 100 bottles in the container, how many of them are likely to be green?

Ans: The experiment implies that 450 out of 1000 bottles are green.

Therefore, out of 100 bottles, 45 are green.

Probability Tree

The tree diagram helps to organize and visualize the different possible outcomes. Branches and ends of the tree are two main positions. Probability of each branch is written on the branch, whereas the ends are containing the final outcome. Tree diagrams are used to figure out when to multiply and when to add. You can see below a tree diagram for the coin:

Types of Probability

There are three major types of probabilities:

Theoretical Probability

Experimental probability, axiomatic probability.

It is based on the possible chances of something to happen. The theoretical probability is mainly based on the reasoning behind probability. For example, if a coin is tossed, the theoretical probability of getting a head will be ½.

It is based on the basis of the observations of an experiment. The experimental probability can be calculated based on the number of possible outcomes by the total number of trials. For example, if a coin is tossed 10 times and head is recorded 6 times then, the experimental probability for heads is 6/10 or, 3/5.

In axiomatic probability, a set of rules or axioms are set which applies to all types. These axioms are set by Kolmogorov and are known as Kolmogorov’s three axioms. With the axiomatic approach to probability, the chances of occurrence or non-occurrence of the events can be quantified. The axiomatic probability lesson covers this concept in detail with Kolmogorov’s three rules (axioms) along with various examples.

Conditional Probability is the likelihood of an event or outcome occurring based on the occurrence of a previous event or outcome.

Probability of an Event

Assume an event E can occur in r ways out of a sum of n probable or possible equally likely ways . Then the probability of happening of the event or its success is expressed as;

The probability that the event will not occur or known as its failure is expressed as:

P(E’) = (n-r)/n = 1-(r/n)

E’ represents that the event will not occur.

Therefore, now we can say;

P(E) + P(E’) = 1

This means that the total of all the probabilities in any random test or experiment is equal to 1.

What are Equally Likely Events?

When the events have the same theoretical probability of happening, then they are called equally likely events. The results of a sample space are called equally likely if all of them have the same probability of occurring. For example, if you throw a die, then the probability of getting 1 is 1/6. Similarly, the probability of getting all the numbers from 2,3,4,5 and 6, one at a time is 1/6. Hence, the following are some examples of equally likely events when throwing a die:

• Getting 3 and 5 on throwing a die
• Getting an even number and an odd number on a die
• Getting 1, 2 or 3 on rolling a die

are equally likely events, since the probabilities of each event are equal.

Complementary Events

The possibility that there will be only two outcomes which states that an event will occur or not. Like a person will come or not come to your house, getting a job or not getting a job, etc. are examples of complementary events. Basically, the complement of an event occurring in the exact opposite that the probability of it is not occurring. Some more examples are:

• It will rain or not rain today
• The student will pass the exam or not pass.
• You win the lottery or you don’t.

Also, read: 

• Independent Events
• Mutually Exclusive Events

Probability Theory

Probability theory had its root in the 16th century when J. Cardan, an Italian mathematician and physician, addressed the first work on the topic, The Book on Games of Chance. After its inception, the knowledge of probability has brought to the attention of great mathematicians. Thus, Probability theory is the branch of mathematics that deals with the possibility of the happening of events. Although there are many distinct probability interpretations, probability theory interprets the concept precisely by expressing it through a set of axioms or hypotheses. These hypotheses help form the probability in terms of a possibility space, which allows a measure holding values between 0 and 1. This is known as the probability measure, to a set of possible outcomes of the sample space.

Probability Density Function

The Probability Density Function (PDF) is the probability function which is represented for the density of a continuous random variable lying between a certain range of values. Probability Density Function explains the normal distribution and how mean and deviation exists. The standard normal distribution is used to create a database or statistics, which are often used in science to represent the real-valued variables, whose distribution is not known.

Probability Terms and Definition

Some of the important probability terms are discussed here:

Applications of Probability

Probability has a wide variety of applications in real life. Some of the common applications which we see in our everyday life while checking the results of the following events:

• Choosing a card from the deck of cards
• Flipping a coin
• Throwing a dice in the air
• Pulling a red ball out of a bucket of red and white balls
• Winning a lucky draw

Other Major Applications of Probability

• It is used for risk assessment and modelling in various industries
• Weather forecasting or prediction of weather changes
• Probability of a team winning in a sport based on players and strength of team
• In the share market, chances of getting the hike of share prices

Problems and Solutions on Probability

Question 1: Find the probability of ‘getting 3 on rolling a die’.

Sample Space = S = {1, 2, 3, 4, 5, 6}

Total number of outcomes = n(S) = 6

Let A be the event of getting 3.

Number of favourable outcomes = n(A) = 1

i.e. A  = {3}

Probability, P(A) = n(A)/n(S) = 1/6

Hence, P(getting 3 on rolling a die) = 1/6

Question 2: Draw a random card from a pack of cards. What is the probability that the card drawn is a face card?

A standard deck has 52 cards.

Total number of outcomes = n(S) = 52

Let E be the event of drawing a face card.

Number of favourable events = n(E) = 4 x 3 = 12 (considered Jack, Queen and King only)

Probability, P = Number of Favourable Outcomes/Total Number of Outcomes

P(E) = n(E)/n(S)

P(the card drawn is a face card) = 3/13

Question 3: A vessel contains 4 blue balls, 5 red balls and 11 white balls. If three balls are drawn from the vessel at random, what is the probability that the first ball is red, the second ball is blue, and the third ball is white?

The probability to get the first ball is red or the first event is 5/20.

Since we have drawn a ball for the first event to occur, then the number of possibilities left for the second event to occur is 20 – 1 = 19.

Hence, the probability of getting the second ball as blue or the second event is 4/19.

Again with the first and second event occurring, the number of possibilities left for the third event to occur is 19 – 1 = 18.

And the probability of the third ball is white or the third event is 11/18.

Therefore, the probability is 5/20 x 4/19 x 11/18 = 44/1368 = 0.032.

Or we can express it as: P = 3.2%.

Question 4: Two dice are rolled, find the probability that the sum is:

• less than 13

Video Lectures

Introduction.

Solving Probability Questions

Probability Important Topics

Probability Important Questions

Probability Problems

• Two dice are thrown together. Find the probability that the product of the numbers on the top of the dice is: (i) 6 (ii) 12 (iii) 7
• A bag contains 10 red, 5 blue and 7 green balls. A ball is drawn at random. Find the probability of this ball being a (i) red ball (ii) green ball (iii) not a blue ball
• All the jacks, queens and kings are removed from a deck of 52 playing cards. The remaining cards are well shuffled and then one card is drawn at random. Giving ace a value 1 similar value for other cards, find the probability that the card has a value (i) 7 (ii) greater than 7 (iii) less than 7
• A die has its six faces marked 0, 1, 1, 1, 6, 6. Two such dice are thrown together and the total score is recorded. (i) How many different scores are possible? (ii) What is the probability of getting a total of 7?

Frequently Asked Questions (FAQs) on Probability

What is probability give an example, what is the formula of probability, what are the different types of probability, what are the basic rules of probability, what is the complement rule in probability.

In probability, the complement rule states that “the sum of probabilities of an event and its complement should be equal to 1”. If A is an event, then the complement rule is given as: P(A) + P(A’) = 1.

What are the different ways to present the probability value?

The three ways to present the probability values are:

• Decimal or fraction

What does the probability of 0 represent?

The probability of 0 represents that the event will not happen or that it is an impossible event.

What is the sample space for tossing two coins?

The sample space for tossing two coins is: S = {HH, HT, TH, TT}

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

good basics concepts provide

Great video content. Perfectly explained for examinations. I really like to learn from BYJU’s

Thank you for your best information on probablity

Good explanation about probability and concept for simple understanding the overall chapter. I hope this is a good way to understand the CONCEPT

For learner of class X standard , it is providing all the relevant informations and approach towards the contenet is knitted in an elegant manner and students will have the opportunity to grasp the topic easily and will be immensely benefited.

this topic has been hard for me but now I know what it is all about and I have really enjoyed it thanks for your good explanation

Well explained

Excellent explanation of probability. One can easily understand about the probability.

I really appreciated your explanations because it’s well understandable Thanks

Love the way you teach

There are 3 boxes Box A contains 10 bulbs out of which 4 are dead box b contains 6 bulbs out of which 1 is dead box c contains 8 bulbs out of which 3 are dead. If a dead bulb is picked at random find the probability that it is from which box?

Probability of selecting a dead bulb from the first box = (1/3) x (4/10) = 4/30 Probability of selecting a dead bulb from the second box = (1/3) x (1/6) = 1/18 Probability of selecting a dead bulb from the third box = (1/3) x (3/8) = 3/24 = 1/8 Total probability = (4/30) + (1/18) + (1/8) = (48 + 20 + 45)360 =113/360

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

General probability rules.

Rule 1: The probability of an impossible event is zero; the probability of a certain event is one. Therefore, for any event A, the range of possible probabilities is: 0 ≤ P(A) ≤ 1

Rule 2: For S the sample space of all possibilities, P(S) = 1. That is the sum of all the probabilities for all possible events is equal to one. Recall the party affiliation above: if you have to belong to one of the three designated political parties, then the sum of P(R), P(D) and P(I) is equal to one.

Rule 3: For any event A, P(A c ) = 1 - P(A). It follows then that P(A) = 1 - P(A c )

Rule 4 (Addition Rule): This is the probability that either one or both events occur

a. If two events, say A and B, are mutually exclusive - that is A and B have no outcomes in common - then P(A or B) = P(A) + P(B)

b. If two events are NOT mutually exclusive, then P(A or B) = P(A) + P(B) - P(A and B)

Rule 5 (Multiplication Rule): This is the probability that both events occur

a. P(A and B) = P(A) • P(B|A) or P(B)*P(A|B) Note: this straight line symbol, |, does not mean divide! This symbols means "conditional" or "given". For instance P(A|B) means the probability that event A occurs given event B has occurred.

b. If A and B are independent - neither event influences or affects the probability that the other event occurs - then P(A and B) = P(A)*P(B). This particular rule extends to more than two independent events. For example, P(A and B and C) = P(A)*P(B)*P(C)

Rule 6 (Conditional Probability): \(P(A|B)=\frac{P(A \ and \ B)}{P(B)}\) or \(P(B|A)=\frac{P(A \ and \ B)}{P(A)}\)