assignment 8 quiz 2 distance formula and applications

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.40: Applications of the Distance Formula

• Last updated
• Save as PDF
• Page ID 4978

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Length between two points based on a right triangle.

Distance Formula in the Coordinate Plane

The distance between two points \((x_1, y_1)\) and \((x_2,y_2)\) can be defined as \(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}\). This is called the distance formula . Remember that distances are always positive!

What if you were given the coordinates of two points? How could you find how far apart these two points are?

Example \(\PageIndex{1}\)

Find the distance between \((-2, -3)\) and \((3, 9)\).

Use the distance formula, plug in the points, and simplify.

\(\begin{align*}d&=\sqrt{(3−(−2))^2+(9−(−3))^2} \\ &=\sqrt{(5)^2+(12)^2} \\ &= \sqrt{25+144} \\ &= \sqrt{169}=13\text{ units }\end{align*}\)

Example \(\PageIndex{2}\)

Find the distance between \((12, 26)\) and \((8, 7)\).

\(\begin{align*}d&=\sqrt{(8−12)^2+(7−26)^2} \\ &= \sqrt{(−4)^2+(−19)^2} \\ &= \sqrt{16+361} \\ &= \sqrt{377}\approx 19.42\text{ units }\end{align*}\)

Example \(\PageIndex{3}\)

Find the distance between \((4, -2)\) and \((-10, 3)\).

Plug in \((4, -2)\) for \((x_1, y_1)\) and \((-10, 3)\) for \((x_2,y_2)\) and simplify.

\(\begin{align*}d&=\sqrt{(−10−4)^2+(3+2)^2} \\ &= \sqrt{(−14)^2+(5)^2} \\ &= \sqrt{196+25} \\ &= \sqrt{221}\approx 14.87\text{ units }\end{align*}\)

Example \(\PageIndex{4}\)

Find the distance between \((3, 4)\) and \((-1, 3)\).

Plug in (3, 4)\) for \((x_1, y_1)\) and \((-1, 3)\) for \((x_2,y_2)\) and simplify.

\(\begin{align*}d &=\sqrt{(−1−3)^2+(3−4)^2} \\ &= \sqrt{(−4)^2+(−1)^2} \\ &= \sqrt{16+1} \\ &= \sqrt{17} \approx 4.12\text{ units }\end{align*}\)

Example \(\PageIndex{5}\)

Find the distance between \((4, 23)\) and \((8, 14)\).

Plug in \((4, 23)\) for \((x_1, y_1)\) and \((8, 14)\) for \((x_2,y_2)\) and simplify.

\(\begin{align*} d&=\sqrt{(8−4)^2+(14−23)^2} \\ &=\sqrt{(4)^2+(−9)^2} \\ &=\sqrt{16+81} \\ & =\sqrt{97} \approx 9.85\text{ units }\end{align*} \)

Find the distance between each pair of points. Round your answer to the nearest hundredth.

• \((4, 15)\) and \((-2, -1)\)
• \((-6, 1)\) and \((9, -11)\)
• \((0, 12)\) and \((-3, 8)\)
• \((-8, 19)\) and \((3, 5)\)
• \((3, -25)\) and \((-10, -7)\)
• \((-1, 2)\) and\((8, -9)\)
• \((5, -2)\) and \((1, 3)\)
• \((-30, 6)\) and \((-23, 0)\)
• \((2, -2)\) and \((2, 5)\)
• \((-9, -4)\) and \((1, -1) \)

Review (Answers)

To see the Review answers, open this PDF file and look for section 3.10.

Additional Resources

Interactive Element

Video: The Distance Formula

Activities: Distance Formula in the Coordinate Plane Discussion Questions

Study Aids: Segments Study Guide

Practice: Applications of the Distance Formula

Real World: Distance Formula in the Coordinate Plane

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 5: Get ready for applying derivatives to analyze functions

About this unit.

Derive and conquer as we apply differentiation to pull out information about the distinguishing features of a function. See how you can identify changes in a function's rate of change and identify its maximum and minimum points.

Maximum and minimum points

• Introduction to minimum and maximum points (Opens a modal)
• Worked example: absolute and relative extrema (Opens a modal)
• Relative maxima and minima Get 3 of 4 questions to level up!
• Absolute maxima and minima Get 3 of 4 questions to level up!

Intervals where a function is positive, negative, increasing, or decreasing

• Increasing, decreasing, positive or negative intervals (Opens a modal)
• Worked example: positive & negative intervals (Opens a modal)
• Positive and negative intervals Get 3 of 4 questions to level up!
• Increasing and decreasing intervals Get 3 of 4 questions to level up!

Interpreting features of graphs

• Graph interpretation word problem: temperature (Opens a modal)
• Graph interpretation word problem: basketball (Opens a modal)
• Graph interpretation word problems Get 3 of 4 questions to level up!

Distance formula

• Distance formula (Opens a modal)
• Distance between two points Get 5 of 7 questions to level up!

Square-root equations

• Intro to square-root equations & extraneous solutions (Opens a modal)
• Square-root equations intro (Opens a modal)
• Intro to solving square-root equations (Opens a modal)
• Solving square-root equations (Opens a modal)
• Solving square-root equations: one solution (Opens a modal)
• Solving square-root equations: two solutions (Opens a modal)
• Solving square-root equations: no solution (Opens a modal)
• Square-root equations intro Get 3 of 4 questions to level up!
• Square-root equations Get 3 of 4 questions to level up!

Zeros of polynomials

• Zeros of polynomials introduction (Opens a modal)
• Zeros of polynomials: plotting zeros (Opens a modal)
• Zeros of polynomials: matching equation to zeros (Opens a modal)
• Zeros of polynomials: matching equation to graph (Opens a modal)
• Zeros of polynomials (with factoring): grouping (Opens a modal)
• Zeros of polynomials (with factoring): common factor (Opens a modal)
• Zeros of polynomials (factored form) Get 3 of 4 questions to level up!
• Zeros of polynomials (with factoring) Get 3 of 4 questions to level up!

Positive and negative intervals of polynomials

• Positive and negative intervals of polynomials (Opens a modal)
• Multiplicity of zeros of polynomials (Opens a modal)
• Zeros of polynomials (multiplicity) (Opens a modal)
• Zeros of polynomials & their graphs (Opens a modal)
• Positive & negative intervals of polynomials (Opens a modal)
• Positive & negative intervals of polynomials Get 3 of 4 questions to level up!
• Zeros of polynomials (multiplicity) Get 3 of 4 questions to level up!

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.2: Distance and Midpoint Formulas and Circles

• Last updated
• Save as PDF
• Page ID 114268

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

Use the Distance Formula

Use the Midpoint Formula

• Write the equation of a circle in standard form
• Graph a circle

Be Prepared 11.1

Before you get started, take this readiness quiz.

Find the length of the hypotenuse of a right triangle whose legs are 12 and 16 inches. If you missed this problem, review Example 2.34.

Be Prepared 11.2

Factor: x 2 − 18 x + 81 . x 2 − 18 x + 81 . If you missed this problem, review Example 6.24.

Be Prepared 11.3

Solve by completing the square: x 2 − 12 x − 12 = 0 . x 2 − 12 x − 12 = 0 . If you missed this problem, review Example 9.22.

In this chapter we will be looking at the conic sections, usually called the conics, and their properties. The conics are curves that result from a plane intersecting a double cone—two cones placed point-to-point. Each half of a double cone is called a nappe.

There are four conics—the circle , parabola , ellipse , and hyperbola . The next figure shows how the plane intersecting the double cone results in each curve.

Each of the curves has many applications that affect your daily life, from your cell phone to acoustics and navigation systems. In this section we will look at the properties of a circle.

We have used the Pythagorean Theorem to find the lengths of the sides of a right triangle. Here we will use this theorem again to find distances on the rectangular coordinate system. By finding distance on the rectangular coordinate system, we can make a connection between the geometry of a conic and algebra—which opens up a world of opportunities for application.

Our first step is to develop a formula to find distances between points on the rectangular coordinate system. We will plot the points and create a right triangle much as we did when we found slope in Graphs and Functions. We then take it one step further and use the Pythagorean Theorem to find the length of the hypotenuse of the triangle—which is the distance between the points.

Example 11.1

Use the rectangular coordinate system to find the distance between the points ( 6 , 4 ) ( 6 , 4 ) and ( 2 , 1 ) . ( 2 , 1 ) .

Try It 11.1

Use the rectangular coordinate system to find the distance between the points ( 6 , 1 ) ( 6 , 1 ) and ( 2 , −2 ) . ( 2 , −2 ) .

Try It 11.2

Use the rectangular coordinate system to find the distance between the points ( 5 , 3 ) ( 5 , 3 ) and ( −3 , −3 ) . ( −3 , −3 ) .

The method we used in the last example leads us to the formula to find the distance between the two points ( x 1 , y 1 ) ( x 1 , y 1 ) and ( x 2 , y 2 ) . ( x 2 , y 2 ) .

When we found the length of the horizontal leg we subtracted 6 − 2 6 − 2 which is x 2 − x 1 . x 2 − x 1 .

When we found the length of the vertical leg we subtracted 4 − 1 4 − 1 which is y 2 − y 1 . y 2 − y 1 .

If the triangle had been in a different position, we may have subtracted x 1 − x 2 x 1 − x 2 or y 1 − y 2 . y 1 − y 2 . The expressions x 2 − x 1 x 2 − x 1 and x 1 − x 2 x 1 − x 2 vary only in the sign of the resulting number. To get the positive value-since distance is positive- we can use absolute value. So to generalize we will say | x 2 − x 1 | | x 2 − x 1 | and | y 2 − y 1 | . | y 2 − y 1 | .

In the Pythagorean Theorem, we substitute the general expressions | x 2 − x 1 | | x 2 − x 1 | and | y 2 − y 1 | | y 2 − y 1 | rather than the numbers.

This is the Distance Formula we use to find the distance d between the two points ( x 1 , y 1 ) ( x 1 , y 1 ) and ( x 2 , y 2 ) . ( x 2 , y 2 ) .

Distance Formula

The distance d between the two points ( x 1 , y 1 ) ( x 1 , y 1 ) and ( x 2 , y 2 ) ( x 2 , y 2 ) is

d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2

Example 11.2

Use the Distance Formula to find the distance between the points ( −5 , −3 ) ( −5 , −3 ) and ( 7 , 2 ) . ( 7 , 2 ) .

Try It 11.3

Use the Distance Formula to find the distance between the points ( −4 , −5 ) ( −4 , −5 ) and ( 5 , 7 ) . ( 5 , 7 ) .

Try It 11.4

Use the Distance Formula to find the distance between the points ( −2 , −5 ) ( −2 , −5 ) and ( −14 , −10 ) . ( −14 , −10 ) .

Example 11.3

Use the Distance Formula to find the distance between the points ( 10 , −4 ) ( 10 , −4 ) and ( −1 , 5 ) . ( −1 , 5 ) . Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

Try It 11.5

Use the Distance Formula to find the distance between the points ( −4 , −5 ) ( −4 , −5 ) and ( 3 , 4 ) . ( 3 , 4 ) . Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

Try It 11.6

Use the Distance Formula to find the distance between the points ( −2 , −5 ) ( −2 , −5 ) and ( −3 , −4 ) . ( −3 , −4 ) . Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

It is often useful to be able to find the midpoint of a segment. For example, if you have the endpoints of the diameter of a circle, you may want to find the center of the circle which is the midpoint of the diameter. To find the midpoint of a line segment, we find the average of the x -coordinates and the average of the y -coordinates of the endpoints.

Midpoint Formula

The midpoint of the line segment whose endpoints are the two points ( x 1 , y 1 ) ( x 1 , y 1 ) and ( x 2 , y 2 ) ( x 2 , y 2 ) is

( x 1 + x 2 2 , y 1 + y 2 2 ) ( x 1 + x 2 2 , y 1 + y 2 2 )

To find the midpoint of a line segment, we find the average of the x -coordinates and the average of the y -coordinates of the endpoints.

Example 11.4

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are ( −5 , −4 ) ( −5 , −4 ) and ( 7 , 2 ) . ( 7 , 2 ) . Plot the endpoints and the midpoint on a rectangular coordinate system.

Try It 11.7

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are ( −3 , −5 ) ( −3 , −5 ) and ( 5 , 7 ) . ( 5 , 7 ) . Plot the endpoints and the midpoint on a rectangular coordinate system.

Try It 11.8

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are ( −2 , −5 ) ( −2 , −5 ) and ( 6 , −1 ) . ( 6 , −1 ) . Plot the endpoints and the midpoint on a rectangular coordinate system.

Both the Distance Formula and the Midpoint Formula depend on two points, ( x 1 , y 1 ) ( x 1 , y 1 ) and ( x 2 , y 2 ) . ( x 2 , y 2 ) . It is easy to confuse which formula requires addition and which subtraction of the coordinates. If we remember where the formulas come from, it may be easier to remember the formulas.

Write the Equation of a Circle in Standard Form

As we mentioned, our goal is to connect the geometry of a conic with algebra. By using the coordinate plane, we are able to do this easily.

We define a circle as all points in a plane that are a fixed distance from a given point in the plane. The given point is called the center, ( h , k ) , ( h , k ) , and the fixed distance is called the radius , r , of the circle.

A circle is all points in a plane that are a fixed distance from a given point in the plane. The given point is called the center , ( h , k ) , ( h , k ) , and the fixed distance is called the radius , r , of the circle.

This is the standard form of the equation of a circle with center, ( h , k ) , ( h , k ) , and radius, r .

Standard Form of the Equation a Circle

The standard form of the equation of a circle with center, ( h , k ) , ( h , k ) , and radius, r , is

Example 11.5

Write the standard form of the equation of the circle with radius 3 and center ( 0 , 0 ) . ( 0 , 0 ) .

Try It 11.9

Write the standard form of the equation of the circle with a radius of 6 and center ( 0 , 0 ) . ( 0 , 0 ) .

Try It 11.10

Write the standard form of the equation of the circle with a radius of 8 and center ( 0 , 0 ) . ( 0 , 0 ) .

In the last example, the center was ( 0 , 0 ) . ( 0 , 0 ) . Notice what happened to the equation. Whenever the center is ( 0 , 0 ) , ( 0 , 0 ) , the standard form becomes x 2 + y 2 = r 2 . x 2 + y 2 = r 2 .

Example 11.6

Write the standard form of the equation of the circle with radius 2 and center ( −1 , 3 ) . ( −1 , 3 ) .

Try It 11.11

Write the standard form of the equation of the circle with a radius of 7 and center ( 2 , −4 ) . ( 2 , −4 ) .

Try It 11.12

Write the standard form of the equation of the circle with a radius of 9 and center ( −3 , −5 ) . ( −3 , −5 ) .

In the next example, the radius is not given. To calculate the radius, we use the Distance Formula with the two given points.

Example 11.7

Write the standard form of the equation of the circle with center ( 2 , 4 ) ( 2 , 4 ) that also contains the point ( −2 , 1 ) . ( −2 , 1 ) .

The radius is the distance from the center to any point on the circle so we can use the distance formula to calculate it. We will use the center ( 2 , 4 ) ( 2 , 4 ) and point ( −2 , 1 ) ( −2 , 1 )

Now that we know the radius, r = 5 , r = 5 , and the center, ( 2 , 4 ) , ( 2 , 4 ) , we can use the standard form of the equation of a circle to find the equation.

Try It 11.13

Write the standard form of the equation of the circle with center ( 2 , 1 ) ( 2 , 1 ) that also contains the point ( −2 , −2 ) . ( −2 , −2 ) .

Try It 11.14

Write the standard form of the equation of the circle with center ( 7 , 1 ) ( 7 , 1 ) that also contains the point ( −1 , −5 ) . ( −1 , −5 ) .

Graph a Circle

Any equation of the form ( x − h ) 2 + ( y − k ) 2 = r 2 ( x − h ) 2 + ( y − k ) 2 = r 2 is the standard form of the equation of a circle with center, ( h , k ) , ( h , k ) , and radius, r. We can then graph the circle on a rectangular coordinate system.

Note that the standard form calls for subtraction from x and y . In the next example, the equation has x + 2 , x + 2 , so we need to rewrite the addition as subtraction of a negative.

Example 11.8

Find the center and radius, then graph the circle: ( x + 2 ) 2 + ( y − 1 ) 2 = 9 . ( x + 2 ) 2 + ( y − 1 ) 2 = 9 .

Try It 11.15

ⓐ Find the center and radius, then ⓑ graph the circle: ( x − 3 ) 2 + ( y + 4 ) 2 = 4 . ( x − 3 ) 2 + ( y + 4 ) 2 = 4 .

Try It 11.16

ⓐ Find the center and radius, then ⓑ graph the circle: ( x − 3 ) 2 + ( y − 1 ) 2 = 16 . ( x − 3 ) 2 + ( y − 1 ) 2 = 16 .

To find the center and radius, we must write the equation in standard form. In the next example, we must first get the coefficient of x 2 , y 2 x 2 , y 2 to be one.

Example 11.9

Find the center and radius and then graph the circle, 4 x 2 + 4 y 2 = 64 . 4 x 2 + 4 y 2 = 64 .

Try It 11.17

ⓐ Find the center and radius, then ⓑ graph the circle: 3 x 2 + 3 y 2 = 27 3 x 2 + 3 y 2 = 27

Try It 11.18

ⓐ Find the center and radius, then ⓑ graph the circle: 5 x 2 + 5 y 2 = 125 5 x 2 + 5 y 2 = 125

If we expand the equation from Example 11.8, ( x + 2 ) 2 + ( y − 1 ) 2 = 9 , ( x + 2 ) 2 + ( y − 1 ) 2 = 9 , the equation of the circle looks very different.

This form of the equation is called the general form of the equation of the circle .

General Form of the Equation of a Circle

The general form of the equation of a circle is

x 2 + y 2 + a x + b y + c = 0 x 2 + y 2 + a x + b y + c = 0

If we are given an equation in general form, we can change it to standard form by completing the squares in both x and y . Then we can graph the circle using its center and radius.

Example 11.10

ⓐ Find the center and radius, then ⓑ graph the circle: x 2 + y 2 − 4 x − 6 y + 4 = 0 . x 2 + y 2 − 4 x − 6 y + 4 = 0 .

We need to rewrite this general form into standard form in order to find the center and radius.

Try It 11.19

ⓐ Find the center and radius, then ⓑ graph the circle: x 2 + y 2 − 6 x − 8 y + 9 = 0 . x 2 + y 2 − 6 x − 8 y + 9 = 0 .

Try It 11.20

ⓐ Find the center and radius, then ⓑ graph the circle: x 2 + y 2 + 6 x − 2 y + 1 = 0 . x 2 + y 2 + 6 x − 2 y + 1 = 0 .

In the next example, there is a y -term and a y 2 y 2 -term. But notice that there is no x -term, only an x 2 x 2 -term. We have seen this before and know that it means h is 0. We will need to complete the square for the y terms, but not for the x terms.

Example 11.11

ⓐ Find the center and radius, then ⓑ graph the circle: x 2 + y 2 + 8 y = 0 . x 2 + y 2 + 8 y = 0 .

Try It 11.21

ⓐ Find the center and radius, then ⓑ graph the circle: x 2 + y 2 − 2 x − 3 = 0 . x 2 + y 2 − 2 x − 3 = 0 .

Try It 11.22

ⓐ Find the center and radius, then ⓑ graph the circle: x 2 + y 2 − 12 y + 11 = 0 . x 2 + y 2 − 12 y + 11 = 0 .

Access these online resources for additional instructions and practice with using the distance and midpoint formulas, and graphing circles.

• Distance-Midpoint Formulas and Circles
• Finding the Distance and Midpoint Between Two Points
• Completing the Square to Write Equation in Standard Form of a Circle

Section 11.1 Exercises

Practice makes perfect.

In the following exercises, find the distance between the points. Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

( 2 , 0 ) ( 2 , 0 ) and ( 5 , 4 ) ( 5 , 4 )

( −4 , −3 ) ( −4 , −3 ) and ( 2 , 5 ) ( 2 , 5 )

( −4 , −3 ) ( −4 , −3 ) and ( 8 , 2 ) ( 8 , 2 )

( −7 , −3 ) ( −7 , −3 ) and ( 8 , 5 ) ( 8 , 5 )

( −1 , 4 ) ( −1 , 4 ) and ( 2 , 0 ) ( 2 , 0 )

( −1 , 3 ) ( −1 , 3 ) and ( 5 , −5 ) ( 5 , −5 )

( 1 , −4 ) ( 1 , −4 ) and ( 6 , 8 ) ( 6 , 8 )

( −8 , −2 ) ( −8 , −2 ) and ( 7 , 6 ) ( 7 , 6 )

( −3 , −5 ) ( −3 , −5 ) and ( 0 , 1 ) ( 0 , 1 )

( −1 , −2 ) ( −1 , −2 ) and ( −3 , 4 ) ( −3 , 4 )

( 3 , −1 ) ( 3 , −1 ) and ( 1 , 7 ) ( 1 , 7 )

( −4 , −5 ) ( −4 , −5 ) and ( 7 , 4 ) ( 7 , 4 )

In the following exercises, ⓐ find the midpoint of the line segments whose endpoints are given and ⓑ plot the endpoints and the midpoint on a rectangular coordinate system.

( 0 , −5 ) ( 0 , −5 ) and ( 4 , −3 ) ( 4 , −3 )

( −2 , −6 ) ( −2 , −6 ) and ( 6 , −2 ) ( 6 , −2 )

( 3 , −1 ) ( 3 , −1 ) and ( 4 , −2 ) ( 4 , −2 )

( −3 , −3 ) ( −3 , −3 ) and ( 6 , −1 ) ( 6 , −1 )

In the following exercises, write the standard form of the equation of the circle with the given radius and center ( 0 , 0 ) . ( 0 , 0 ) .

Radius: 2 2

Radius: 5 5

In the following exercises, write the standard form of the equation of the circle with the given radius and center

Radius: 1, center: ( 3 , 5 ) ( 3 , 5 )

Radius: 10, center: ( −2 , 6 ) ( −2 , 6 )

Radius: 2.5 , 2.5 , center: ( 1.5 , −3.5 ) ( 1.5 , −3.5 )

Radius: 1.5 , 1.5 , center: ( −5.5 , −6.5 ) ( −5.5 , −6.5 )

For the following exercises, write the standard form of the equation of the circle with the given center with point on the circle.

Center ( 3 , −2 ) ( 3 , −2 ) with point ( 3 , 6 ) ( 3 , 6 )

Center ( 6 , −6 ) ( 6 , −6 ) with point ( 2 , −3 ) ( 2 , −3 )

Center ( 4 , 4 ) ( 4 , 4 ) with point ( 2 , 2 ) ( 2 , 2 )

Center ( −5 , 6 ) ( −5 , 6 ) with point ( −2 , 3 ) ( −2 , 3 )

In the following exercises, ⓐ find the center and radius, then ⓑ graph each circle.

( x + 5 ) 2 + ( y + 3 ) 2 = 1 ( x + 5 ) 2 + ( y + 3 ) 2 = 1

( x − 2 ) 2 + ( y − 3 ) 2 = 9 ( x − 2 ) 2 + ( y − 3 ) 2 = 9

( x − 4 ) 2 + ( y + 2 ) 2 = 16 ( x − 4 ) 2 + ( y + 2 ) 2 = 16

( x + 2 ) 2 + ( y − 5 ) 2 = 4 ( x + 2 ) 2 + ( y − 5 ) 2 = 4

x 2 + ( y + 2 ) 2 = 25 x 2 + ( y + 2 ) 2 = 25

( x − 1 ) 2 + y 2 = 36 ( x − 1 ) 2 + y 2 = 36

( x − 1.5 ) 2 + ( y + 2.5 ) 2 = 0.25 ( x − 1.5 ) 2 + ( y + 2.5 ) 2 = 0.25

( x − 1 ) 2 + ( y − 3 ) 2 = 9 4 ( x − 1 ) 2 + ( y − 3 ) 2 = 9 4

x 2 + y 2 = 64 x 2 + y 2 = 64

x 2 + y 2 = 49 x 2 + y 2 = 49

2 x 2 + 2 y 2 = 8 2 x 2 + 2 y 2 = 8

6 x 2 + 6 y 2 = 216 6 x 2 + 6 y 2 = 216

In the following exercises, ⓐ identify the center and radius and ⓑ graph.

x 2 + y 2 + 2 x + 6 y + 9 = 0 x 2 + y 2 + 2 x + 6 y + 9 = 0

x 2 + y 2 − 6 x − 8 y = 0 x 2 + y 2 − 6 x − 8 y = 0

x 2 + y 2 − 4 x + 10 y − 7 = 0 x 2 + y 2 − 4 x + 10 y − 7 = 0

x 2 + y 2 + 12 x − 14 y + 21 = 0 x 2 + y 2 + 12 x − 14 y + 21 = 0

x 2 + y 2 + 6 y + 5 = 0 x 2 + y 2 + 6 y + 5 = 0

x 2 + y 2 − 10 y = 0 x 2 + y 2 − 10 y = 0

x 2 + y 2 + 4 x = 0 x 2 + y 2 + 4 x = 0

x 2 + y 2 − 14 x + 13 = 0 x 2 + y 2 − 14 x + 13 = 0

Writing Exercises

Explain the relationship between the distance formula and the equation of a circle.

Is a circle a function? Explain why or why not.

In your own words, state the definition of a circle.

In your own words, explain the steps you would take to change the general form of the equation of a circle to the standard form.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ If most of your checks were:

…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.

…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Whom can you ask for help?Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?

…no - I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.

Have an account?

distance formula

8th - 9th grade, mathematics.

40 questions

Introducing new   Paper mode

No student devices needed.   Know more

• 2. Multiple Choice Edit 3 minutes 1 pt Find the distance between (-4, 5) and (7, 18). 15.96 16.08 16.23 17.03
• 3. Multiple Choice Edit 3 minutes 1 pt Find the distance between (-3, -11) and (8, -42). 32.1 32.3 32.7 32.9
• 4. Multiple Choice Edit 3 minutes 1 pt Find the distance between (3, 24) and (7, 56). 32.1 32.2 32.3 32.4
• 5. Multiple Choice Edit 3 minutes 1 pt Find the distance between (2, -75) and (10, 235). 305.5 308.6 310.1 315.3
• 6. Multiple Choice Edit 3 minutes 1 pt Find the distance between (-5, -8) and (-1, -16). 8.9 9.8 10.3 11
• 7. Multiple Choice Edit 3 minutes 1 pt Find the distance between (-12, 1) and (12, -1). 24.05 24.06 24.07 24.08
• 8. Multiple Choice Edit 3 minutes 1 pt What is the distance between (2,9) and (1,5)? 15 17 4.12 3.87
• 11. Multiple Choice Edit 3 minutes 1 pt John leaves school to go home. He walks 6 blocks North and then 8 blocks west. How far is John from the school?  14 blocks 12 blocks 10 blocks 8.5 blocks
• 12. Multiple Choice Edit 3 minutes 1 pt Find the distance between (-4, 5) and (7, 18). 15.96 16.08 16.23 17.03
• 14. Multiple Choice Edit 15 minutes 1 pt Find the distance between (2, -75) and (10, 235). 305.5 308.6 310.1 315.3
• 15. Multiple Choice Edit 15 minutes 1 pt Find the distance between (-5, -8) and (-1, -16). 8.9 9.8 10.3 11
• 16. Multiple Choice Edit 15 minutes 1 pt Find the distance between (-12, 1) and (12, -1). 24.05 24.06 24.07 24.08
• 18. Multiple Choice Edit 1 minute 1 pt Becky leaves school to go home. She walks 6 blocks North and then 8 blocks west. How far is Becky from the school?  14 blocks 12 blocks 10 blocks 8.5 blocks
• 20. Multiple Choice Edit 15 minutes 1 pt What is the distance between (-5, 3) and (4, -5). √-145 √145 145 -145
• 21. Multiple Choice Edit 15 minutes 1 pt What is the distance between (2,9) and (1,5)? 15 17 4.12 3.87
• 28. Multiple Choice Edit 15 minutes 1 pt What is the opposite of squaring a number? divide multiply  fractions square root
• 33. Multiple Choice Edit 15 minutes 1 pt Seth made a small rectangular table for his workroom.  The sides of the table are 36" and 18".  If the diagonal of the table measures 43", is the table square?  A table which is "square" has right angles at the corners.  Yes No
• 34. Multiple Choice Edit 15 minutes 1 pt A suitcase measures 24 inches long and 18 inches high.  What is the diagonal length of the suitcase to the nearest tenth of a foot?  2.5 2.9 26.5 30.0
• 35. Multiple Choice Edit 15 minutes 1 pt To get from point A to point B you must avoid walking through a pond.  To avoid the pond, you must walk 34 meters south and 41 meters east.  To the nearest meter, how many meters would be saved if it were possible to walk through the pond? 22 34 53 75
• 37. Multiple Choice Edit 15 minutes 1 pt John leaves school to go home. He walks 6 blocks North and then 8 blocks west. How far is John from the school?  14 blocks 12 blocks 10 blocks 8.5 blocks
• 39. Multiple Choice Edit 15 minutes 1 pt The pythagorean Theorem ONLY works on which triangle?  obtuse scalene isosceles right

Explore all questions with a free account

Continue with email

Continue with phone

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes
• Applications of Heron's Formula
• 3D Distance Formula
• Real-Life Applications of Speed, Distance and Time
• Great Circle Distance Formula
• Real Life Applications of Area
• Stopping Distance Formula
• Distance Traveled Formula
• Applications of Trigonometry in Real Life
• Linear Approximation Formula
• Real-Life Applications of Perimeter
• Euclidean Distance - Formula, Derivation & Solved Examples
• Speed Time Distance Formula
• Law of Cosines Great Circle Distance in R
• Area of a Circle: Formula, Derivation, Examples
• How to Create a Distance Matrix in R?
• Applications of Dijkstra's shortest path algorithm
• How to Calculate Manhattan Distance in R?
• How to Calculate Euclidean Distance in R?
• Rate of Change Formula

Applications of Distance Formula

Distance formula is a fundamental concept in math that estimates the distance between two points in a plane with coordinates. It is used in several real-world situations including transportation, navigation, physics and engineering among others, as highlighted. The understanding of the distance formula allows us to find solutions for practical problems that involve patterns in space and how to get the best routes and trajectories.

In this article we shall learn the applications of the distance formula in everyday scenarios, and others in detail.

Table of Content

What is Distance Formula?

Real life applications on distance formula, navigation and gps systems, surveying and cartography, physics and engineering, network analysis and optimization, urban planning and traffic management, robotics and automation.

Distance formula is a mathematical expression, to find the distance between two points in a coordinate plane. It is a theorem, which was derived by Pythagoras and can be used in two-dimensional as well as three-dimensional figures. The distance formula is represented as:

Distance Formula = √(x 2 – x 1 ) 2 + (y 2 – y 1 ) 2

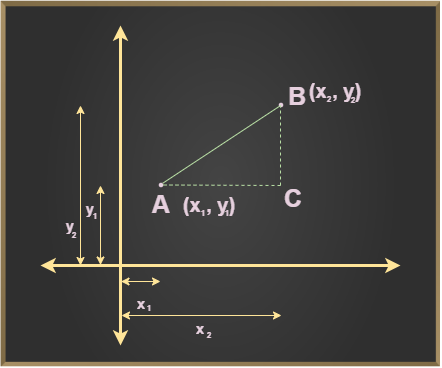
Distance Formula

In three-dimensional space, the distance formula is extended to include the z coordinates:

Distance Formula = √(x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 + (z 2 – z 1 ) 2

Some common applications of the distance formula include:

• Robotics and Automation: Distance formula serves as the basis for path planning and obstacle avoidance in robotics. Robots can use the sonar to determine the distance to an obstacle and therefore, move through difficult situations more carefully.
• Sports Analytics: Sports analysts use the formula for distance determination to evaluate distances travelled by athletes during the session training and in the competition. This data will be useful in measuring the player performances and identifying the training programs.
• Urban Planning and Traffic Management: Urban planners utilise the distance formula mainly to analyze traffic and design transport networks which are optimal. It aids in the selection of the best positions for transportation centres and in intensifying mobility in urban areas.
• Telecommunications and Signal Processing: Engineers deal with distance formulas and they use them for calculation of signal propagation delays and for optimization of antenna placement. It reduces waste and leads to better communication network architecture and increased coverage areas.
• Computer Graphics and Animation: Distance formula is part of computer graphics and used in order to calculate distances between objects in virtual setting. It aids in the development of actual scenarios and cinematic effects which is seen in video games and movies.

Various real life applications of distance formula observed in the real life includes:

One of the major applications of distance formula is in navigation tools and GPS systems where it is applied to calculate the shortest route between two such points (A,B) on maps. GPS devices, which make use of the distance formula and can compute the distance covered and give directions of the last destination to drivers very precisely. With Distance formula, navigation systems easily perform optimal route adjustments, time savings and effective travel management.

Example: GPS navigation system employ distance formula which indicates the shortest distance between the current location of a vehicle and in terms what will be its destination. Through the access to this data, drivers can select the fastest route based on real-time data like traffic congestion issues, road closings, etc.

Surveyors and cartographers make use of the distance formula in order to measure precise distances between landmarks, boundaries and geographical features. The distance formula which is employed by the surveyors helps them to create the finest maps for the real estates, property boundaries, and have their survey at the correct places. Cartographers are able to tell distances on maps and quite precisely represent geographic relationships with the help of distance formula.

Example: Surveyors, while contouring land to a particular construction project, use the distance formula to calculate the various distances between property lines, building structures and topography features. Having such data as a basis of infrastructure projects deliberation, planning, and provision of roads and buildings and utilities is of utmost importance.

In physics and engineering, the distance formula is used in order to find the distances between the objects in outer space, and determine the trajectories for these objects. Engineers are working to find the the motion of missiles, motor vehicles, and celestial bodies, predicting their paths and velocities correctly. The popular use of the distance formula among the physicists is to investigate the physical phenomena, like gravity and electrical field.

Example: Spatial engineers apply the distance formula to elaborate space vehicle trajectories to make them fly around planets and other celestial bodies. The use of distance formula allows calculating the distance traveled fairly easy and thus, the engineers can plan their orbital maneuvers and ensure precise navigation in missions in space.

distance formula has a key role in network analysis and optimization on the basis of which nodes can be connected to each other via the shortest connection path. Network analysts utilize distance formula to optimize communication systems, transportation systems, and supply chains in a way that reduces travel time and increases effectiveness. Through distance formula, network designers can find out drifted points, arrange sequence better and enhance overall network performance.

Example: Logistics companies rely on the distance formula to arrange delivery routes and decrease the transportation costs. Through the means of computing the shortest path between logistic centers, warehouses, and delivery terminals, the companies can essentially simplify their supply chains and eventually enhance customer satisfaction.

Distance formula is widely used by urban planners and transport engineers for tackling traffic distribution and design of transportation networks as well as local amenities. It is used to calculate the distances between the main transport hubs, like bus stops, train points, metro stations, etc., and evaluate the accessibility and connection within urban parts.

Example: Urban designers employ a distance formula to find the best places to situate public transportation stops and stations; they take into account the number of people, traffic patterns, and land use. Urban planners counts on carefully arranging traffic hubs to achieve mobility, decreasing of congestion, and improving urban living in general.

Robotics and automation make use of distance formula for trajectory planning and operations on obstructions. Robots measure distances to obstacles in their environment using distance formula and by this way they are able to avoid collisions with them and tackle complex environment. It enables robots to find out the shortest path to reach a target location while avoiding hitting the obstacles that may be encountered on the way.

Example: Autonomous vehicles use the distance formula to calculate the distance between the vehicle and objects around it, like other vehicles, pedestrians, and roadside obstacles. Such data helps provide autonomous systems with real-time decision making functions which also enable it to navigate through traffic unscathed.

Related Articles:

Distance Formula in Coordinate Geometry Real-Life Applications of Speed, Distance and Time

FAQs on Applications of Distance Formula

What is the distance formula, and how is it used in real-life applications.

Distance formula calculates the distance between any two points on a coordinate plane, It is used in real-life in various fields such as navigation, surveying, physics, engineering, and environmental sciences.

How do GPS systems use the distance formula for navigation?

Utilizations of the GPS technology involves the use of distance formula in order to determine the shortest distance between two foreseen location on the map, and offering accurate route description to the drivers, hence saving time in travel.

In what ways do surveyors and cartographers apply the distance formula?

Surveyors and cartographer make use of distance formula to calculate the distances between landmarks, boundaries, and geographical features. This process is done to facilitate the creation of detailed maps and land surveys with a high degree of accuracy.

How is the distance formula used in physics and engineering?

In Physics and engineering use the distance formula to study the motion of space objects, to calculate trajectories of moving objects, and to predict relationships in spatial phenomena.

What role does the distance formula play in network analysis and optimization?

Distance formula is one of the most things used in networking analysis which help to determine the shortest possible path between two nodes in the network, thus improving the efficiency of the communication networks, transportation networks and supply chains.

Please Login to comment...

Similar reads.

• Real Life Application
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?