introduction to machine learning assignment 3 2023

• Publications
• Student Projects

Introduction to Machine Learning (2023)

Introduction.

• [05.02.2024] The 2024 winter exam and the respective solutions catalog (source file used for the grading) are now online!
• [13.08.2023] The 2023 summer exam and the respective solutions, and solutions catalog (source file used for the grading) are now online!
• [01.08.2023] The lecture notes have been updated. We have two new chapters: Clustering (provisional and not yet proof-read by the professors) and Probabilistic modelling .
• [13.07.2023] (Exam review session) There will be an exam review session on 31 July from 10-12 in ETA F 5. This will be held by Andisheh Amrollani and Mohammad Reza Karimi who were in charge of exams for the years of 2021 and 2022. They will solve the previous exam year’s questions as voted by you on Moodle and answer general questions you might have about the exam. Here is the vote on Moodle: https://moodle-app2.let.ethz.ch/mod/choice/view.php?id=920239 .
• [13.07.2023] (Plagiarism checks) We have finished plagiarism checks for the projects. If you have not received an email accusing you of plagiarism and you have a grade of 4 or above in the projects you are eligible to take the exam. If you do not satisfy any of the two above requirements, we ask you to deregister from the exam (deadline for online de-registration is 30 July). If you are not eligible and do not de-register we will give you a NO-SHOW grade.
• [13.07.2023]  (Attendance only doctoral students) Your grades will be passed by tomorrow.
• [04.07.2023] We have added the exam for 2021 winter together with its solution, please find them in the Performance Assessment section.
• [24.06.2023] The lecture notes have been updated. We have two new chapters: Chapter 8 Neural Networks and Chapter 9 PCA . More coming soon!
• [07.06.2023] The two exams for 2022 academic year have been posted in the exam section to help you familiarize the exam contents.
• [07.06.2023] Project grades have been emailed. They are still subject to plagiarism checks.
• [31.05.2023] There will be a Q&A next Wednesday (07 June) presenting solutions for Project 4.
• [30.05.2023] There will be NO lectures held this week on Tuesday (30 May) and Wednesday (31 May). There still WILL BE a tutorial on Friday (2 June), as usual at 2pm, on large language models.
• [02.05.2023] A new version of the lecture notes is released! This version includes two new chapters: Chapter 6 Model Evaluation and Selection and Chapter 7 Bias-Variance Tradeoff and Regularization . In case you have anything to report, please contact Xinyu Sun .
• [03.04.2023] Because of the Easter break, there is no tutorial for this week on Friday (07.04). Instead, the session will be recorded and put online.
• [14.03.2023] For students who do not want to solve projects on their personal laptops, check out this guide by Vukasin Bozic explaining how to use Euler, the scientific computer clusters of ETH. More information regarding Euler is available here .
• [07.03.2023] The Projects and FAQ section have been updated. Importantly there will be a project introduction session on each Wednesday the project is released. And a project solution session on the Wednesday the week after the project deadline. Both to be held at the Q&A session 17(sharp)-18.
• [02.03.2023] Project 0 is online. It is ungraded and aims to help you familiarize the project workflow.
• [27.02.2023] Regarding the Q&A on March 1st: Introduction to Python for Data Science (jupyter, numpy, pandas, seaborn, matplotlib). Please check the README before the tutorial. This is for installing all the necessary libraries so you can follow along during the tutorial.
• [22.02.2023] During the Q&A session on March 1st, Olga Mineeva and Stefan Stark will present a Python libraries introduction covering Numpy and Pandas.
• [10.02.2023] Welcome to the course Introduction to Machine Learning!

Lecture Notes

Q&a sessions, questions & answers, code projects, performance assessment, other resources.

• Marc Peter Deisenroth, A Aldo Faisal, and Cheng Soon Ong Mathematics for Machine Learning . Cambridge University Press, 2020.
• K. Murphy. Machine Learning: a Probabilistic Perspective . MIT Press, 2012.
• C. Bishop. Pattern Recognition and Machine Learning . Springer, 2007. (optional)
• T. Hastie, R. Tibshirani, and J. Friedman. The Elements of Statistical Learning: Data Mining, Inference and Prediction . Springer, 2001.
• L. Wasserman. All of Statistics: A Concise Course in Statistical Inference. Springer, 2004.
• G. James., D. Witten and et al. An Introduction to Statistical Learning . Springer, 2021.

CS480/680 Winter 2023 - Introduction to Machine Learning

• Create a Python notebook in Google Colab
• Click on "edit", then "notebook settings" and select "None" (CPU), "GPU" or "TPU" for hardware acceleration.
• A1: out Jan 16, due Jan 27 (11:59 pm)
• A2: out Jan 30, due Feb 10 (11:59 pm)
• A3: out Feb 13, due Mar 3 (11:59 pm)
• A4: out Mar 6, due Mar 17 (11:59 pm)
• A5: out Mar 20, due Mar 31 (11:59 pm)

On the due date of an assignment, the work done to date should be submitted electronically on the LEARN website; further material may be submitted with a 2% penalty for every rounded up hour past the deadline. For example, an assignment submitted 5 hours and 15 min late will receive a penalty of ceiling(5.25) * 2% = 12%. Assignments submitted more than 50 hours late will not be marked.

Assignment 1: due Jan 27 (11:59 pm)

• Part 1 (5 points): K-nearest neighbours
• Download the dataset for K-nearest neighbours: knn-dataset.zip
• Origin: this data is a modified version of the Optical Recognition of Handwritten Digits Dataset from the UCI repository. It contains pre-processed black and white images of the digits 5 and 6. Each feature indicates how many pixels are black in a patch of 4 x 4 pixels.
• Format: there is one row per image and one column per feature. The class labels are 5 and 6. The label on line n in train_labels.csv is the label for the data point on line n in train_inputs.csv.
• Implement k-nearest neighbours by filling in the functions in the skeleton code: cs480_winter23_asst1_knn_skeleton.ipynb
• Do not import any additional library. Feel free to run the Jupyter notebook on any machine or Google Colab. Google Colab is a free cloud environment provided by Google that allows you to run Jupyter notebooks very easily. Python and all necessary libraries are already installed.
• Once you are done filling in all the functions, run the Jupyter notebook entirely and save the following results:
• A graph that shows the average accuracy based on 10-fold cross validation when varying the number of neighbours from 1 to 30.
• The best number of neighbours found by 10-fold cross validation and its cross-validation accuracy.
• The test accuracy based on the best number of neighbours
• Upload to LEARN your Jupyter notebook with the results saved. Do not submit a zip file or pdf file. The TAs will run some of the Jupyter notebooks to verify the results.
• Part 2 (5 points): Linear regression
• Download the dataset for linear regression: regression-dataset.zip
• Origin: this data consists of samples from a 2D surface that you can plot to visualize how linear regression is working.
• Format: there is one row per data point and one column per feature. The targets are real values. The target on line n in train_targets.csv is the target for the data point on line n in train_inputs.csv.
• Implement linear regression by filling in the functions in the skeleton code: cs480_winter23_asst1_linear_regression_skeleton.ipynb
• A graph that shows the average mean squared error based on 10-fold cross validation when varying the lambda hyperparameter from 0 to 3 in increments of 0.1.
• The best lambda found by 10-fold cross validation and its cross validation mean squared error.
• The test mean squared error based on the best lambda.
• Derive a closed-form expression for the estimate of w that minimizes the objective. Show the steps along the way, not just the final estimates.
• Show that this objective is equivalent to the negative log-likelihood for linear regression where each data point may have a different Gaussian measurement noise. What is the variance of each measurement noise in this model?
• Upload to LEARN a pdf file with your answers for the two previous questions.

Assignment 2: due Feb 10 (11:59 pm)

In this assignment, you will implement logistic regression. Then you will test your implementations on a small dataset.

• Dataset: Use the same dataset as for the K-nearest neighbour in Assignment 1
• Algorithm implementation: Implement logistic regression based on gradient descent and Newton's algorithm by filling in the functions in the skeleton code. The skeleton code consists of a Python Jupyter notebook:
• Logistic regression skeleton: cs480_winter23_asst2_logistic_regression_skeleton.ipynb
• Do not import any additional library. Feel free to run the Jupyter notebooks on any machine or Google Colab. Google Colab is a free cloud environment provided by Google that allows you to run Jupyter notebooks very easily. Python and all necessary libraries are already installed.
• Submission via LEARN: Jupyter notebook
• Results: Once you are done filling in all the functions, run the Jupyter notebook entirely and save the results. For the purpose of the assignment, use the default values included in the skeleton code for max_iters, gradient_norm_threshold and learning_rate. Make sure that the following results are saved:
• Gradient descent (4 points):
• Graph that shows the negative log probabilties based on 10-fold cross validation when varying the lambda hyperparameter from 0 to 25 in increments of 1 .
• The best lambda found by 10-fold cross validation and its cross validation negative log probability.
• The test negative log probability and the test accuracy based on the best lambda
• The number of iterations of gradient descent for the best lambda
• Newton's algorithm (4 points):
• The number of iterations of Newton's algorithm for the best lambda
• Discussion: At the end of the Jupyter notebook, add a text cell and answer the following questions:
• Question 2 (2 points): Logistic regression finds a linear separator where as k-Nearest Neighbours (in Assignment 1) finds a non-linear separator. Compare the expressivity of the separators. Discuss under what circumstances each type of separator is expected to perform best. What could explain the results obtained with KNN in comparison to the results obtained with logistic regression?
• Question 3 (3 points): Is the training set used in this assignment linearly separable? To answer this question, add some code to the Jupyter Notebook that uses a logistic regression classifier to determine whether the training set is linearly separable. Add some text that explains why this code can determine the linear separability of a dataset. Indicate whether the training set is linearly separable based on the results.

Assignment 3: due March 3 (11:59 pm)

In this assignment, you will experiment with fully connected neural networks and convolutional neural networks, using the PyTorch package. PyTorch facilitates the design of neural networks, automatic differentiation and accelerated computation with GPUs and multi-core CPUs. Preliminary steps:

• Familiarize yourself with PyTorch by going through the tutorial Get familiar with PyTorch: a 60 minute blitz
• Download and install PyTorch on a machine with a GPU or use Google's Colaboratory environment , which allows you to run PyTorch code on a GPU in the cloud. Colab already has PyTorch pre-installed. To enable GPU acceleration, click on "edit", then "notebook settings" and select "GPU" for hardware acceleration. It is also possible to select "TPU", but the PyTorch code provided with this assignment will need to be modified in a non-trivial way to take advantage of TPU acceleration. Note that you can complete this assignment without any GPU (or TPU). Any computer that has several cores will also provide some degree of acceleration.
• Download the base code for this assignment: cs480_winter23_asst3_cnn_cifar10.ipynb . (bug in the test function corrected on Feb 26: the test function now returns the averag_test_loss instead of the average_train_loss)

Answer the following questions by modifying the base code in cs480_winter23_asst3_cnn_cifar10.ipynb. Submit the modified Jupyter notebook via LEARN.

• Part 1 (3 points) Architecture: Compare the accuracy of the convolutional neural network in the file cs480_winter23_asst3_cnn_cifar10.ipynb on the cifar10 dataset to the accuracy of simple dense neural networks with 0, 1, 2 and 3 hidden layers of 512 rectified linear units each. Run the code in the file cs480_winter23_asst3_cnn_cifar10.ipynb without changing the parameters to train a convolutional neural network. Then, modify the code in cs480_winter23_asst3_cnn_cifar10.ipynb to obtain simple dense neural networks with 0, 1, 2 and 3 hidden layers of 512 rectified linear units. Produce two graphs that contain 5 curves (one for the convolutional neural net and one for each dense neural net of 0-3 hidden layers). The y-axis is the accuracy and the x-axis is the number of epochs (# of passes through the training set). Produce one graph where all the curves correspond to the training accuracy and a second graph where all the curves correspond to the test accuracy. Train the neural networks for 10 epochs. Save the following results in your Jupyter notebook:
• The two graphs for training and testing accuracy.
• Add some text to the Jupyter notebook to explain the results (i.e., why some models perform better or worse than other models).
• Part 2 (2 point) Activation functions: Compare the accuracy achieved by rectified linear units and sigmoid units in the convolutional neural network in cs480_winter23_asst3_cnn_cifar10.ipynb. Modify the code in cs480_winter23_asst3_cnn_cifar10.ipynb to use sigmoid units. Produce two graphs (one for training accuracy and one for test accuracy) that each contain 2 curves (one for rectified linear units and another one for sigmoid units). The y-axis is the accuracy and the x-axis is the number of epochs. Train the neural networks for 10 epochs. Save the following results in your Jupyter notebook:
• The two graphs for training and test accuracy.
• Add some text to the Jupyter notebook to explain the results (i.e., why one model performs better or worse than the other model).
• Part 3 (2 points) Dropout: Compare the accuracy achieved with and without dropout in the convolutional neural network in cs480_winter23_asst3_cnn_cifar10.ipynb. Modify the code in cs480_winter23_asst3_cnn_cifar10.ipynb by inserting a dropout probability of 0.25 after each max pooling layer and a dropout probability of 0.5 after the hidden fully connected layer. Produce two graphs (one for training accuracy and the other one for testing accuracy) that each contain 2 curves (with and without dropout). The y-axis is the accuracy and the x-axis is the number of epochs. Produce curves for 20 epochs.
• Add some text to the Jupyter notebook to explain the results (i.e., why did one model perform better than the other one).
• Part 4 (2 point) Optimizers: Compare the accuracy achieved when training the convolutional neural network in cs480_winter23_asst3_cnn_cifar10.ipynb with four different optimizers: SGD (learning rate = 0.001), RMSprop (learning rate = 0.0001), Adagrad (default parameters) and Adam (default parameters). Modify the code in cs480_winter23_asst3_cnn_cifar10.ipynb to use the SGD, Adagrad and RMSprop optimizers. Produce two graphs (one for training accuracy and the other one for testing accuracy) that each contain 4 curves (for SGD, RMSprop, Adagrad and Adam). The y-axis is the accuracy and the x-axis is the number of epochs. Produce curves up to 10 epochs.
• Add some text to the Jupyter notebook to explain the results (i.e., why did some optimizers perform better or worse than other optimizers).
• Part 5 (3 points) Filters: Compare the accuracy of the convolutional neural network in cs480_winter23_asst3_cnn_cifar10.ipynb with a modified version that replaces each stack of (Conv2d, Activation, Max pooling) layers with 5x5 filters by a deeper stack of (Conv2d, Activation, Conv2d, Activation, Max Pooling) layers with 3x3 filters. Produce two graphs (one for training accuracy and the other one for testing accuracy) that each contain 2 curves (for 3x3 filters and 5x5 filters). The y-axis is the accuracy and the x-axis is the number of epochs. Produce curves up to 10 epochs.
• Add some text to the Jupyter notebook to explain the results (i.e., why did one architecture perform better or worse than the other architecture).
• Part 6 (3 points) Theory: Show that a neural network that uses the tanh activation function can represent the same space of functions as another neural network that uses sigmoid activation functions instead of tanh activation functions. More preciseley, let f(x) = W (1) tanh(W (2) x + b (2) ) + b (1) be a two-layer neural network that uses the tanh activation function for the hidden layer. Design a mathematically equivalent neural network g(x) that uses the sigmoid activation function instead of tanh. Show that f(x)=g(x).

Assignment 4: due March 17 (11:59 pm)

In this assignment, you will experiment with various types of recurrent neural networks (RNNs) and transformers in PyTorch.

• Download the base code for this assignment:
• Part 1: cs480_winter23_asst4_char_rnn_classification.ipynb
• Part 2: cs480_winter23_asst4_char_rnn_generation.ipynb
• Part 3: cs480_winter23_asst4_seq2seq_translation.ipynb

Answer the following questions by modifying the base code in each notebook. Submit the modified Jupyter notebooks via LEARN.

• Part 1 (5 points): Encoder implementation in cs480_winter23_asst4_char_rnn_classification.ipynb . Compare the accuracy of the encoder when varying the type of hidden units: linear units, gated recurrent units (GRUs) and long short term memory (LSTM) units. For linear hidden units, just run the script of the Jupyter notebook as it is. For GRUs and LSTMs, modify the base code. Save the following results in your Jupyter notebook:
• Two graphs that each contain 3 curves (linear hidden units, GRUs and LSTM units). The first graph displays the training loss and the second graph displays the validation loss. In both graphs, the y-axis is the negative log likelihood and the x-axis is the number of thousands of iterations.
• For each type of hidden unit, print the test loss and the test confusion matrix of the model that achieved the best validation loss among all iterations (i.e., one best test loss and test confusion matrix per type of hidden unit).
• Explanation of the results (i.e., why some hidden units perform better or worse than other units).
• Part 2 (5 points): Decoder implementation in cs480_winter23_asst4_char_rnn_generation.ipynb . Compare the accuracy of the decoder when varying the information fed as input to the hidden units at each time step: i) previous hidden unit, previous character and category; ii) previous hidden unit and previous character; iii) previous hidden unit and category; iv) previous hidden unit. For i), just run the Python notebook as it is. For ii) and iv) modify the code to feed the category as input to the hidden unit(s) of the first time steps only. For iii) and iv), modify the code to avoid feeding the previous character as input to each hidden unit. Save the following results in your Jupyter notebook:
• Two graphs that each contain 4 curves (i, ii, iii, iv). The first graph displays the training loss and the second graph displays the validation loss. In both graphs, the y-axis is the negative log likelihood and the x-axis is the number of 500 iterations.
• For each architecture, print the test loss of the model that achieved the best validation loss among all iterations (i.e., one best test loss per architecture).
• Explanation of the results (i.e., how does the type of information fed to the hidden units affect the results).
• Part 3 (5 points): Seq2seq implementation in cs480_winter23_asst4_seq2seq_translation.ipynb . Compare the accuracy of RNN seq2seq models with and without attention as well as a transformer. To keep the running time reasonable, use a hidden_size of 32 (in practice, a hidden size of at least 512 would be used, but for the purpose of this assignment, use 32). Test the translation models on sentences of MAX_LENGTH = 5 and 10. For the RNN seq2seq model with attention (hidden_size=32 and MAX_LENGTH=5), just run the base code as it is. For the RNN seq2seq model without attention, modify the base code to call the DecoderRNN class (without attention) already provided. For the transformer model, use the nn.TransformerEncoder, nn.TransformerDecoder or nn.Transformer classes in the PyTorch library and modify any part of the base code that you see fit. Set the parameters of the transfomer to match those of the RNN see2seq models whenever possible (i.e., d_model=32), otherwise feel free to choose suitable parameters. Save the following results in your Jupyter notebook:
• Four graphs that each contain 3 curves (RNN seq2seq with attention and RNN seq2seq without attention and transformer). The first and second graphs display the training loss and the validation loss respectively for sentences of MAX_LENGTH=5. The third and fourth graphs display the training loss and validation loss respectively for sentences of MAX_LENGTH=10. In all graphs, the y-axis is the negative log likelihood and the x-axis is the number of thousands of iterations.
• For each architecture tested with sentences of MAX_LENGTH=5, print the test loss of the model that achieved the best validation loss among all iterations (i.e., one best test loss per architecture). Similarly, for each architecture tested with sentences of MAX_LENGTH=10, print the test loss of the model that achieved the best validation loss among all iterations (i.e., one best test loss per architecture).
• Explanation of the results (i.e., how does the attention and architecture of each model affects the results?).

Assignment 5: due March 31 (11:59 pm)

In this assignment, you will implement a variational auto-encoder (VAE) and a generative adversarial network (GAN) in PyTorch to generate images similar to those in the MNIST dataset. As a starting point, the code for a deterministic auto-encoder (DAE) is provided. While DAEs achieve good reconstruction of the original images, they struggle to generate new images that are similar to those in MNIST. Implement a VAE and GAN to generate better images. Download the skeleton code for this assignment:

• Part 1: cs480_winter23_asst5_vae_skeleton.ipynb
• Part 2: cs480_winter23_asst5_gan_skeleton.ipynb

Fill in the functions in each skeleton notebook and answer the following questions in each notebook. Submit the Jupyter notebooks via LEARN.

• Part 1 (7 points): VAE implementation in cs480_winter23_asst5_vae_skeleton.ipynb . Fill in the functions and save the following results in your Jupyter notebook:
• Two graphs that each contain 2 curves (DAE and VAE). The first graph displays the training reconstruction loss and the second graph displays the testing reconstruction loss. In both graphs, the y-axis is binary cross entropy and the x-axis is the number of epochs.
• Print a sample of generated images after each epoch of training for both DAEs and VAEs.
• Explanation of the results (i.e., compare and explain the binary cross entropy and the quality of the sampled images generated by DAEs and VAEs).
• Part 2 (8 points): GAN implementation in cs480_winter23_asst5_gan_skeleton.ipynb . Checkout the following tutorial for GANs . Fill in the functions and save the following results in your Jupyter notebook:
• Two graphs that each contain 2 curves (Generator and Discriminator losses). The first graph displays the training loss and the second graph displays the testing loss. In both graphs, the y-axis is binary cross entropy and the x-axis is the number of epochs.
• Print a sample of generated images after each epoch of training for your GAN.
• Explanation of the results (i.e., compare and explain the quality of the sampled images generated by VAEs and GANs).

Introduction to Machine Learning

Final announcements.

Congratulations on the end of the semester in 6.390 -- the staff has greatly enjoyed working you! We hope that you enjoyed the course and wish you the best!

Course letter grades have been submitted to the Registrar. The grade is available through WebSIS.

The final exam statistics are: median 78.75, mean 76.48, and standard deviation 12.14.

In our letter grade calculations, we gave an additional +4 point offset on the final exam to everyone (but the offset will not show up in Gradescope or your Progress page).

We do not have regrade requests/window for the final exam. If you have strong evidence that (1) a grading error has been made, and (2) the error will affect your letter grade, please email [email protected] with a well-written technical explanation of the error for consideration.

We hope that everyone has a wonderful summer!

Announcements for Week 13 (Week of May 14)

Thank you to those who've filled out the end-of-term subject evaluations . If you haven't done so yet, we'd love to hear about your thoughts on 6.390. This provides valuable feedback for us and other students, for future semesters; thank you!

Our last class will be on Monday May 15, on the topic of transformers. This topic will not be included in the final exam.

On Wednesday May 17, we will hold optional instructors office hours 9:30am-12:30pm and 1-4pm, in 34-501 (and only 34-501). Please feel free to bring any questions you may have while preparing for the final.

The 20-day extensions are applicable up through the end of the day on Wednesday May 17. The application will be updated on your Progress page on Thursday May 18.

• Our last regular office hours will be held on Thursday May 18.

The final exam will be held in person, on Tuesday May 23, from 1:30 PM to 4:30 PM, at Johnson Track . Please review the final info page for logistics and practice materials .

Announcements for Week 12 (Week of May 7)

The end-of-term subject evaluations have opened. We'd love to hear about your thoughts on 6.390. This provides valuable feedback for us and other students, for future semesters; thank you!

The final exam will be held in person, on Tuesday, May 23 2023, from 1:30 PM to 4:30 PM, in Johnson Track . Please review final exam info page for logistics and practice materials.

As we near the end of the semester, several elements of this week (and wrap up of previous Week 11 assignments) will proceed as usual, but with some key differences due to MIT end of term regulations, as noted below.

Exercise 12 are due Monday, May 8, 9am.

Lab 11 checkoffs are due Monday, May 8, 11pm.

Homework 11 is due Wednesday, May 10, 11pm.

Homework 12 will release at 9am, Monday, May 8. It is due Friday, May 12, 11:59pm.

Lab 12 will release in lab sessions on Wednesday, March 10. Checkoffs are due Friday, May 12, 11:59pm.

• 20-day extensions are applicable up through the end of the day on Wednesday May 17.

Announcements for Week 11 (Week of April 30)

The final exam will be held in person, on Tuesday, May 23 2023, from 1:30 PM to 4:30 PM, in Johnson Track . Please review final exam page for logistics, practice materials, and deadline for requesting accommodations.

Assignments due this week:

Exercises for week 11 are due Monday, May 1, 9am.

Lab for week 10 checkoffs are due Monday, May 1, 11pm.

Homework for week 10 is due Wednesday, May 3, 11pm.

Assignments releases this week:

Homework for week 11 will release at 9am, Monday, May 1. (It is due Wednesday, May 10, 11pm.)

Lab for week 11 will release in lab sessions on Wednesday, May 3. (Checkoffs are due Monday, May 8, 11pm.)

Exercises for week 12 will release at 5pm, Wednesday, May 3. (They are due Monday, May 8, 9am.)

Announcements for Week 10 (week of April 23)

Exercises for week 10 are due Monday, April 24, 9am.

Lab for week 9 checkoffs are due Monday, April 24, 11pm.

Homework for week 9 is due Wednesday, April 26, 11pm.

Homework for week 10 will release at 9am, Monday, April 24. (It is due Wednesday, May 3, 11pm.)

Lab for week 10 will release in lab sessions on Wednesday, April 26. (Checkoffs are due Monday, May 1, 11pm.)

Exercises for week 11 will release at 5pm, Wednesday, April 26. (They are due Monday, May 1, 9am.)

Announcements for Week 9 (Week of April 16)

Related to the Patriots' Day Institute Holiday, recitations and office hours will be cancelled on Monday, April 17. Enjoy the holiday!

Lab for week 8 checkoffs are due Monday, April 17, 11pm.

Exercises for week 9 are due Wednesday, April 19, 9am.

Homework for week 8 is due Wednesday, April 19, 11pm.

Homework for week 9 will release at 9am, Monday, April 17. (It is due Wednesday, April 26, 11pm.)

Lab for week 9 will release in lab sessions on Wednesday, April 19. (Checkoffs are due Monday, April 24, 11pm.)

Exercises for week 10 will release at 5pm, Wednesday, April 19. (They are due Monday, April 24, 9am.)

Announcements for Week 8 (Week of April 9)

Exercises for week 8 are due Monday, April 10, 9am.

Lab for week 7 checkoffs are due Monday, April 10, 11pm.

Homework for week 7 is due Wednesday, April 12, 11pm.

Homework for week 8 will release at 9am, Monday, April 10. (It is due Wednesday, April 19, 11pm.)

Lab for week 8 will release in lab sessions on Wednesday, April 12. (Checkoffs are due Monday, April 17, 11pm.)

Exercises for week 9 will release at 5pm, Wednesday, April 12. (They are due Wednesday, April 19, 9am.)

Heads up: related to the Patriots' Day Institute Holiday next week, recitation and office hours will be cancelled on Monday, April 17.

Announcements for Week 7 (Week of April 2)

We hope that everyone had a good spring break!

We resume our normal class meeting schedule this week (and office hours resume on Sunday April 2).

• Exercises for week 7 are due Monday, April 3, 9am.

Homework for week 7 will release at 9am, Monday, April 3. (It is due Wednesday, April 12, 11pm.)

Lab for week 7 will release in lab sessions on Wednesday, April 5. (Checkoffs are due Monday, April 10, 11pm.)

Exercises for week 8 will release at 5pm, Wednesday, April 5. (They are due Monday, April 10, 9am.)

Midterm Results

The midterm grades have been released on Gradescope . You will need to log in with your MIT email for Gradescope access (this applies to cross-registered students as well). The median score is 80, the mean is 77.7, and the standard deviation is 12.5.

You can review the midterm exam and midterm solutions .

Regrade requests must be made on Gradescope , and must include a clear statement and justification for reconsideration for specific questions(s) and part(s) that you seek a regrade on. Our grading review in response to a regrade request can result in no change, addition of points, or reduction of points; we may also review grading on the rest of your midterm to correct for other grading mistakes, if any.

Requests for midterm regrades will open after Spring Break on Sunday, Apr. 2 at 9am , and close on Wednesday, Apr. 5 at 11pm .

We hope that everyone has a good Spring Break!

Announcements for the Midterm Week (Mon, Mar. 20 - Fri, Mar. 24)

The midterm exam will be held on Thursday, March 23, 7:30pm-9:30pm. You should review midterm logistics , including about selecting your exam room , and practice midterms .

There are no Monday/Wednesday classes scheduled this week.

All regular office hours will be held as usual this week.

On Monday March 20, we will hold optional informal instructors office hours during the normal class times (9:30am-12:30pm, and 1-4pm) in 34-501 (and only 34-501). Please feel free to bring any questions you may have while preparing for the midterm.

Lab for week 6 checkoffs are due Monday, March 20, 11pm.

Homework for week 6 is due Wednesday, March 22, 11pm.

• Exercises for week 7 will release at 9am, Friday, March 24. (They will be due Monday, April 3, 9am.)

Announcements for Week 6 (Mon, Mar. 13 - Fri, Mar. 17)

The midterm exam will be held on Thursday, March 23, 7:30pm-9:30pm. You should review midterm logistics , including about selecting your exam room , requesting conflict exam or accommodations by March 13 , and practice midterms.

Exercises for week 6 are due Monday, March 13, 9am.

Lab for week 5 checkoffs are due Monday, March 13, 11pm.

Homework for week 5 is due Wednesday, March 15, 11pm.

Homework for week 6 will release at 9am, Monday, March 13. (It is due Wednesday, March 22, 11pm.)

Lab for week 6 will release in lab sessions on Wednesday, March 15. (Checkoffs are due Monday, March 20, 11pm.)

Announcements for Week 5 (Mon, Mar. 6 - Fri, Mar. 10)

The midterm exam will be held on Thursday, March 23 2023, 7:30pm-9:30pm. You should review midterm logistics , including about selecting your midterm room, deadline for requesting conflict exam or accommodations, and practice midterms.

The Registrar has posted the MIT Final Exams Schedule . The 6.390 final will be held on Tuesday, May 23 2023, 1:30pm-4:30pm, in Johnson Track . The Registrar will also schedule a Conflict Exam for 6.390, and will announce that schedule after Drop Date (April 25). For cross-registered 6.390 students who have a schedule conflict with the May 23 final exam, we expect to make the 6.390 conflict exam time (as scheduled by the MIT Registrar) available as well.

There is a student in our class who needs copies of class notes as an approved accommodation. If you're interested in serving as a paid note taker, please reach out to DAS , at 617-253-1674 or [email protected] . More details of the job can be found here .

Exercises for week 5 are due Monday, March 6, 9am.

Lab for week 4 checkoffs are due Monday, March 6, 11pm.

Homework for week 4 is due Wednesday, March 8, 11pm.

Homework for week 5 will release at 9am, Monday, March 6. (It is due Wednesday, March 15, 11pm.)

Lab for week 5 will release in lab sessions on Wednesday, March 8. (Checkoffs are due Monday, March 13, 11pm.)

Exercises for week 6 will releaseat 5pm, Wednesday, March 8. (They are due Monday, March 13, 9am.)

We have enabled psetpartners for 6.390, for those of you interested in being matched up with other classmates to work on course materials/assignments. It looks like the next match date for 6.390 is Friday, March 10.

Announcements for Week 4 (Mon, Feb. 27 - Fri, Mar. 3)

The Registrar has posted the MIT Final Exams Schedule . The 6.390 final will be held on Tuesday, May 23 2023, from 1:30 PM to 4:30 PM Eastern Time, in Johnson Track . The Registrar will also schedule a Conflict Exam for 6.390, and will announce that schedule after Drop Date (April 25). For cross-registered 6.390 students who have a schedule conflict with the May 23 final exam, we expect to make the 6.390 conflict exam time (as scheduled by the MIT Registrar) available as well.

Exercises for week 4 are due Monday, Feb 27, 9am.

Lab for week 3 checkoffs are due Monday, Feb 27, 11pm.

Homework for week 3 is due Wednesday, March 1, 11pm.

Homework for week 4 will release at 9am, Monday, Feb 27. (It is due Wednesday, March 1, 11pm.)

Lab for week 4 will release in lab sessions on Wednesday, March 1. (Checkoffs are due Monday, March 6, 11pm.)

Exercises for week 5 will releaseat 5pm, Wednesday, March 1. (They are due Monday, March 6, 9am.)

We have enabled psetpartners for 6.390, for those of you interested in being matched up with other classmates to work on course materials/assignments. It looks like the next match date for 6.390 is Friday, March 3.

Announcements for Week 3 (Mon, 20 Feb - Fri, 24 Feb)

Related to the Institute Holiday on Monday Feb 20, we will be meeting on Tuesday Feb 21 for our recitation sessions.

Office hours schedules are adjusted this week:

Regular Monday office hours (7-9pm and 9-11pm) will be held on Tuesday Feb 21 (7-9pm in 32-044 and 9-11pm virtually).

Regular Tuesday office hours (4-6pm and 7-9pm) will be cancelled on Feb 21.

Exercises for week 3 are due Tuesday, Feb 21, 9am. (typically exercises are due 9am before recitation on Mondays.)

Lab for week 2 checkoffs are due Monday, Feb 20, 11pm.

Homework for week 2 is due Wednesday, Feb 22, 11pm.

Homework for week 3 will release at 9am, Monday, Feb 20 (It is due Wednesday, March 1, 11pm)

Lab for week 3 will release in lab sessions on Wednesday, Feb 22. (Checkoffs are due Monday, Feb 27, 11pm.)

Exercises for week 4 will releaseat 5pm, Wednesday, Feb 22. (They are due Monday, Feb 27, 9am).

Tips: Keep an eye out for 6.390 announcements on 6.390 Home Page . Use the Calendar for release and access to all of the assignments and content. Use the Progress page for keeping track of assignments due and progress.

For both regular Monday and Wednesday class meetings, you may attend your assigned section only. If you need to change your permanent section assignment, you will be able to self-switch with "Section Signup" through Canvas, subject to section capacity constraints. Self-switching will be open between Feb 6, 5:00pm and Feb 20, 11:59pm; changes made on Canvas will be synced to our site here every 10min.

We have enabled psetpartners for 6.390, for those of you interested in being matched up with other classmates to work on course materials/assignments. It looks like the next match date for 6.390 is Friday, Feb 24.

Announcements for Week 2 (Mon, 13 Feb - Fri, 17 Feb)

Tip: Keep an eye out for 6.390 announcements on 6.390 Home Page . Use the Calendar for release and access to all of the assignments and content. Use the Progress page for keeping track of assignments due and progress.

Exercises for week 2 have been released (as of Wednesday, Feb. 8, 5pm). They are due 9am Monday morning before recitation on Feb. 13.

If you missed the Lab for week 1 on Wednesday, Feb. 8, do not worry; you can still work the questions on the lab and have a checkoff in Office Hours for full credit before the lab checkoff due (Monday, Feb. 13 at 11pm).

Homework for week 1 is due by Wednesday, Feb. 15 at 11pm.

Homework for week 2 will release at 9am on Monday, Feb. 13; it will be due Wednesday, Feb. 22, at 11pm.

For both Monday and Wednesday class meetings, you may attend your assigned section only. If you need to change your permanent section assignment, you can self-switch with "Section Signup" through Canvas, subject to section capacity constraints. Self-switching is open between Feb. 6, 5:00pm and Feb. 20, 11:59pm; changes made on Canvas will be synced to our site here every 10min.

We have enabled psetpartners for 6.390, for those of you interested in being matched up with other classmates to work on course materials/assignments. It looks like the next match date for 6.390 is Friday, Feb. 17.

Announcements for Week 1 (Mon, 6 Feb - Fri, 10 Feb)

After the first class meeting, you may attend your assigned section only. If you need to change your permanent section assignment, you will be able to self-switch with "Section Signup" through Canvas, subject to section capacity constraints. Self-switching will be open between Feb 6, 5:00pm and Feb 20, 11:59pm; changes made on Canvas will be synced to our site here every 10min.

We have enabled psetpartners for 6.390, for those of you interested in being matched up with other classmates to work on course materials/assignments.

If you cross-registered late and do not have an MIT Kerberos yet to login to our website; do not worry. All week 1 course materials will be made publicly viewable, through links on Calendar . Feel free to follow along and submit when your account is ready.

First Class Meeting

Our first class meeting is a recitation on Monday, Feb. 6. If you pre-registered for 6.390, the Registrar likely scheduled you into a section. Our seven section time/room can be found here . If at all possible, please attend the section you are scheduled into by the Registrar for this first session (this helps ensuring everyone would have a seat/table). If you registered later and don't have a section, please come to Section 1, 3, 5, or 7, on Feb 6 to get started.

Pre-semester Information

👋 Hi there! Welcome to 6.390! We're very much looking forward to working with you all this spring!

1. Course Overview

6.390 introduces principles, algorithms, and applications of machine learning from the point of view of modeling and prediction. Topics include e.g. formulation of learning problems; representation, over-fitting, generalization; classification, regression, reinforcement learning, sequence learning, clustering; classical and neural-network methods.

For reference, here is our fall22 syllabus.

2. Prerequisites

Concretely, things we expect you to know (we use these constantly, but don’t teach them explicitly):

Programming

• Intermediate Python, including the notion of classes.
• Exposure to algorithms – ability to understand & discuss pseudo-code, and implement in Python.

Linear Algebra

• Fundamental matrix manipulations, e.g., transpose, multiplication, and inverse.
• Points and planes in high-dimensional space.
• Basic matrix calculus, e.g., gradients.

6.1010 [6.009] or 6.1210 [6.006] can serve as the programming prerequisite. 18.06, 18.C06, 18.03, or 18.700 can serve as the linear algebra prerequisite.

3. Useful Background

Things it helps to have prior exposure to, but we don’t expect (we use these in 6.390, but will discuss as we go):

• numpy (Python package for matrix/linear algebra).
• pytorch (Python package for neural networks).
• Basic discrete probability, e.g., random variables, conditioning, and expectation.

4. Class Meeting and Sections

We will be meeting on Mondays and Wednesdays. We have seven sections and you can meet our staff here .

If at all possible, please attend the section you are scheduled into by the Registrar for this first session . Subsequently, we'll have a mechanism through which you can make changes in your scheduled section. Self-switching will be first-come-first-served and subject to section capacity constraints; the process will be detailed here.

5. Course Number Change

Since fall22, all MIT EECS (Course 6) subjects have been renumbered (rationale and details can be found here ). This subject used to be called 6.036; moving forward, we'll refer to it internally as 6.390 ("six three-nine-oh"). But for registration purposes, please register for 6.3900 (note the extra zero).

6. Cross-registration

This site is our course site and it uses MIT Kerberos for authentication. Cross-registered students will receive their Kerberos once the registration goes through; however, the process can take a while. We therefore strongly encourage you to cross register early if possible, to avoid delayed access to course materials.

We follow MIT's calendar, and do not have additional extensions or accommodations based on home university calendar. Especially important will be for you to plan ahead for our two in-person exams. We'll have a midterm exam on March 23 (in the week before MIT's Spring Break). We'll also have a final exam during MIT's final exam week, Friday May 19 through Wednesday May 24; the final is to be scheduled by the Registrar.

If you're not familiar with MIT campus, you might find the whereis site helpful.

7. Listeners

Due to capacity and other constraints, we will not accept Listener registrants in 6.390 this semester.

8. Other Questions?

Feel free to drop us an email at [email protected] . We'd love to hear from you!

NPTEL Introduction to Machine Learning Assignment 3 Answers 2023

NPTEL Introduction to Machine Learning Assignment 3 Answers 2023:- In This article, we have provided the answers of Introduction to Machine Learning Assignment 3 You must submit your assignment to your own knowledge.

NPTEL Introduction To Machine Learning Week 3 Assignment Answer 2023

1. Which of the following are differences between LDA and Logistic Regression?

• Logistic Regression is typically suited for binary classification, whereas LDA is directly applicable to multi-class problems
• Logistic Regression is robust to outliers whereas LDA is sensiti v e to outliers
• both (a) and (b)
• None of these

2. We have two classes in our dataset. The two classes have the same mean but different variance.

LDA can classify them perfectly. LDA can NOT classify them perf e ctly. LDA is not applicable in data with these properties Insufficient information

3. We have two classes in our dataset. The two classes have the same variance but different mean.

LDA can classify them perfectly. LDA can NOT classify them perfectly. LDA is not applicable in data with these prop e rties Insufficient information

4. Given the following distribution of data points:

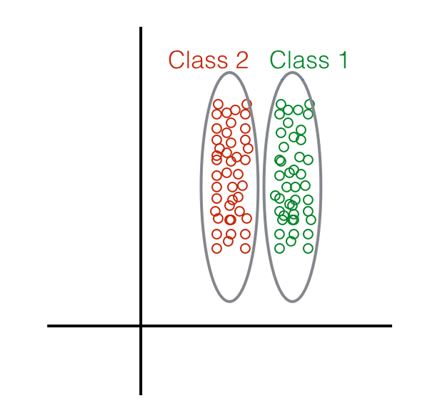
What method would you choose to perform Dimensionality Red u ction? Linear Discriminant Analysis Principal Component Analysis Both LDA and/or PCA. None of the above.

5. If log(1−p(x)/1+p(x))=β0+βx Wha t is p(x) ?

p(x)=1+eβ0+βx / eβ0+βx p(x)=1+eβ0+βx / 1−eβ0+βx p(x)=eβ0+βx / 1+eβ0+βx p(x)=1−eβ0+βx / 1+eβ0+βx

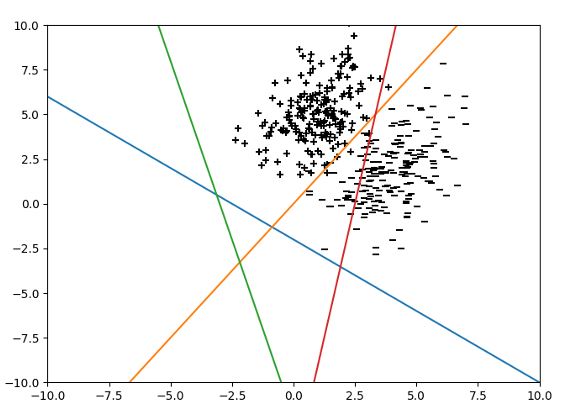
Red Orange Blue Green

7. Which of these techniques do we use to optimise Logistic Regres s ion:

Least S q uare Error Maximum Likelihood (a) or (b) are equally good (a) and (b) perform very poorly, so we generally avoid using Logistic Regression None of these

8. LDA assumes that the class data is distributed as:

Poisson Unif o rm Gaussian LDA makes no such assumption.

9. Suppose we have two variables, X and Y (the dependent variable), and we wish to find their relation. An expert tells us that relation between the two has the form Y=meX+c. Suppose the samples of the variables X and Y are available to us. Is it possible to apply linear regression to this data to estimate the values of m and c ?

No. Yes. Insufficient information. None of the above.

10. What might happen to our logistic regression model if the number of features is more th a n the number of samples in our dataset?

It will remain unaffected It will not find a hyperplane as the decision bound a ry It will over fit None of the above

NPTEL Introduction to Machine Learning Assignment 3 Answers [July 2022]

1. For linear classification we use: a. A linear function to separate the classes. b . A linear function to model the data. c. A linear loss. d. Non-linear function to fit the data.

2. Logit transformation for Pr(X=1) for given data is S=[0,1,1 , 0,1,0,1] a. 3/4 b. 4/3 c. 4/7 d . 3/7

Answers will be Uploaded Shortly and it will be Notified on Telegram, So  JOIN NOW

3. The output of binary class logistic regression lies in this range. a. [−∞,∞] b. [−1,1] c. [0,1] d. [−∞ , 0]

4. If log(1−p(x)1+p(x))=β0+βxlog What is p(x)p(x)?

5. Logistic regression is robust to outliers. Why? a . The squashing of output values between [0, 1] dampens the affect of outliers. b. Linear models are robust to outliers. c. The parameters in logistic regression tend to take small values due to the nature of the problem setting and hence outliers get translated to the same range as other samples. d. The given statement is false.

6. Aim of LDA is (multiple options may apply) a. Minimize intra-class variability. b. Maximize intra-class variability. c . Minimize the distance between the mean of classes d. Maximize the distance between the mean of classes

👇 For Week 04 Assignment Answers 👇

7. We have two classes in our dataset with mean 0 and 1, and variance 2 and 3. a. LDA may be able to classify them perfectly. b. LDA will definitely be able to classify them perfectly. c. LDA will definitely NOT be able to classify them perfectly . d. None of the above.

8. We have two classes in our dataset with mean 0 and 5 , and variance 1 and 2. a. LDA may be able to classify them perfectly. b. LDA will definitely be able to classify them perfectly. c. LDA will definitely NOT be able to classify them perfectly. d. None of the above.

9. For the two classes ’+ ’ and ’-’ shown below. While performing LDA on it, which line is the most appropriate for projecting data points? a. Red b. Orange c. Blue d. Green

10. LDA assumes that the class data is distributed as: a. Poisson b. Uniform c. Gaussian d. LDA makes no such assumption .

For More NPTEL Answers:-  CLICK HERE Join Our Telegram:-  CLICK HERE

What is Introduction to Machine Learning?

With the increased availability of data from varied sources there has been increasing attention paid to the various data driven disciplines such as analytics and machine learning. In this course we intend to introduce some of the basic concepts of machine learning from a mathematically well motivated perspective. We will cover the different learning paradigms and some of the more popular algorithms and architectures used in each of these paradigms.

CRITERIA TO GET A CERTIFICATE

Average assignment score = 25% of the average of best 8 assignments out of the total 12 assignments given in the course. Exam score = 75% of the proctored certification exam score out of 100

Final score = Average assignment score + Exam score

YOU WILL BE ELIGIBLE FOR A CERTIFICATE ONLY IF THE AVERAGE ASSIGNMENT SCORE >=10/25 AND EXAM SCORE >= 30/75. If one of the 2 criteria is not met, you will not get the certificate even if the Final score >= 40/100.

NPTEL Introduction to Machine Learning Assignment 3 Answers [Jan 2022]

Q1. consider the case where two classes follow Gaussian distribution which are centered at (6, 8) and (−6, −4) and have identity covariance matrix. Which of the following is the separating decision boundary using LDA assuming the priors to be equal?

(A) x+y=2 (B) y−x=2 (C) x=y (D) both (a) and (b) (E) None of the above (F) Can not be found from the given information

Answer:- (A) x+y=2

👇 FOR NEXT WEEK ASSIGNMENT ANSWERS 👇

Q2. Which of the following are differences between PCR and LDA?

(A) PCR is unsupervised whereas LDA is supervised (B) PCR maximizes the variance in the data whereas LDA maximizes the separation between the classes (C) both (a) and (b) (D) None of these

Answer:- (A) PCR is unsupervised whereas LDA is supervised

Q3. Which of the following are differences between LDA and Logistic Regression?

(A) Logistic Regression is typically suited for binary classification, whereas LDA is directly applicable to multi-class problems (B) Logistic Regression is robust to outliers whereas LDA is sensitive to outliers (C) both (a) and (b) (D) None of these

Answer:- (C) both (a) and (b)

ALSO READ :- NPTEL Registration Steps [July – Dec 2022] NPTEL Exam Pattern Tips & Top Tricks [2022] NPTEL Exam Result 2022 | NPTEL Swayam Result Download

Q4. We have two classes in our dataset. The two classes have the same mean but different variance.

• LDA can classify them perfectly.
• LDA can NOT classify them perfectly.
• LDA is not applicable in data with these properties
• Insufficient information

Answer:- 2. LDA can NOT classify them perfectly.

Q5. We have two classes in our dataset. The two classes have the same variance but different mean.

Answer:- 1. LDA can classify them perfectly.

Q6. Which of these techniques do we use to optimise Logistic Regression:

• Least Square Error
• Maximum Likelihood
• (a) or (b) are equally good
• (a) and (b) perform very poorly, so we generally avoid using Logistic Regression

Answer:- 2.Maximum Likelihood

Q7. Suppose we have two variables, X and Y (the dependent variable), and we wish to find their relation. An expert tells us that relation between the two has the form Y = meX + c . Suppose the samples of the variables X and Y are available to us. Is it possible to apply linear regression to this data to estimate the values of m and c ?

• insufficient information

Answer:- 2.yes

Q8. What might happen to our logistic regression model if the number of features is more than the number of samples in our dataset?

• It will remain unaffected
• It will not find a hyperplane as the decision boundary
• It will overfit
• None of the above

Answer:- 3. It will overfit

Q9. Logistic regression also has an application in

• Regression problems
• Sensitivity analysis
• Both (a) and (b)

Answer:- 3. Both (a) and (b)

Q10. Consider the following datasets:

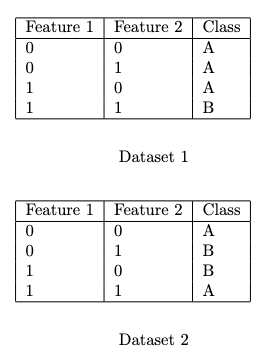
Which of these datasets can you achieve zero training error using Logistic Regression (without any additional feature transformations)?

• Both the datasets
• Only on dataset 1
• Only on dataset 2
• None of the datasets

Answer:- For Answer Click Here

NPTEL Introduction to Machine Learning Assignment 3 Answers 2022:- In This article, we have provided the answers of Introduction to Machine Learning Assignment 3

Disclaimer :- We do not claim 100% surety of solutions, these solutions are based on our sole expertise, and by using posting these answers we are simply looking to help students as a reference, so we urge do your assignment on your own.

For More NPTEL Answers:-  CLICK HERE

Join Our Telegram:-  CLICK HERE

4 thoughts on “NPTEL Introduction to Machine Learning Assignment 3 Answers 2023”

• Pingback: NPTEL Introduction To Machine Learning Assignment 4 Answers
• Pingback: NPTEL Introduction To Machine Learning Assignment 5 Answers
• Pingback: NPTEL Introduction To Machine Learning Assignment 6 Answers
• Pingback: NPTEL Introduction To Machine Learning Assignment 7 Answers

Leave a Comment Cancel reply

You must be logged in to post a comment.

Please Enable JavaScript in your Browser to Visit this Site.

This class introduces algorithms for learning , which constitute an important part of artificial intelligence.

Useful Links

Prerequisites.

If you want to brush up on prerequisite material:

Both textbooks for this class are available free online. Hardcover and eTextbook versions are also available.

Homework and Exams

You have a total of 5 slip days that you can apply to your semester's homework. We will simply not award points for any late homework you submit that would bring your total slip days over five. If you are in the Disabled Students' Program and you are offered an extension, even with your extension plus slip days combined, no single assignment can be extended more than 5 days . (We have to grade them sometime!) this Extension Requests form . -->

The following homework due dates are tentative and may change.

Homework 1 is due Wednesday, January 24 at 11:59 PM . (Warning: 16 MB zipfile. Here's just the written part .)

Homework 2 is due Wednesday, February 7 at 11:59 PM . (PDF file only.)

Homework 3 is due Friday, February 23 at 11:59 PM . (Warning: 15 MB zipfile. Here's just the written part .)

Homework 4 is due Friday, March 8 at 11:59 PM . (Here's just the written part .)

Homework 5 is due Tuesday, April 2 at 11:59 PM . (Here's just the written part .)

Homework 6 is due Friday, April 19 at 11:59 PM . (Warning: 137 MB zipfile. Here's just the written part .) Important: For Homework 6 only, the “HW6 Code” assignment on Gradescope has an autograder for some parts of the homework. The grade you receive on the coding questions will directly reflect the score reported by the autograder!

Homework 7 is due Wednesday, May 1 at 11:59 PM . (Warning: 116 MB zipfile. Here's just the written part .)

The CS 289A Project has a proposal due Friday, April 12 . The video is due Monday, May 6 , and the final report is due Tuesday, May 7 . this Google spreadsheet . Dates are available from April 1 to April 5 . -->

The Midterm took place on Monday, March 11 at 6:30–8:00 PM in multiple rooms on campus. Previous midterms are available: Without solutions: Spring 2013 , Spring 2014 , Spring 2015 , Fall 2015 , Spring 2016 , Spring 2017 , Spring 2019 , Summer 2019 , Spring 2020 Midterm A , Spring 2020 Midterm B , Spring 2021 , Spring 2022 , Spring 2023 , Spring 2024 . With solutions: Spring 2013 , Spring 2014 , Spring 2015 , Fall 2015 , Spring 2016 , Spring 2017 , Spring 2019 , Summer 2019 , Spring 2020 Midterm A , Spring 2020 Midterm B , Spring 2021 , Spring 2022 , Spring 2023 , Spring 2024 .

The Final Exam took place on Friday, May 10 at 3–6 PM in four different rooms on campus. (Check Ed Discussions for your room.) Previous final exams are available. Without solutions: Spring 2013 , Spring 2014 , Spring 2015 , Fall 2015 , Spring 2016 , Spring 2017 , Spring 2019 , Spring 2020 , Spring 2021 , Spring 2022 , Spring 2023 , Spring 2024 . With solutions: Spring 2013 , Spring 2014 , Spring 2015 , Fall 2015 , Spring 2016 , Spring 2017 , Spring 2019 , Spring 2020 , Spring 2021 , Spring 2022 , Spring 2023 , Spring 2024 .

Now available: The complete semester's lecture notes (with table of contents and introduction) .

Lecture 1 (January 17): Introduction. Classification. Training, validation, and testing. Overfitting and underfitting. Read ESL, Chapter 1. My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 2 (January 22): Linear classifiers. Decision functions and decision boundaries. The centroid method. Perceptrons. Read parts of the Wikipedia Perceptron page. Optional: Read ESL, Section 4.5–4.5.1. My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 3 (January 24): Gradient descent, stochastic gradient descent, and the perceptron learning algorithm. Feature space versus weight space. The maximum margin classifier, aka hard-margin support vector machine (SVM). Read ISL, Section 9–9.1. My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 4 (January 29): The support vector classifier, aka soft-margin support vector machine (SVM). Features and nonlinear decision boundaries. Read ESL, Section 12.2 up to and including the first paragraph of 12.2.1. My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 5 (January 31): Machine learning abstractions: application/data, model, optimization problem, optimization algorithm. Common types of optimization problems: unconstrained, linear programs, quadratic programs. The influence of the step size on gradient descent. Optional: Read (selectively) the Wikipedia page on mathematical optimization . My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 6 (February 5): Decision theory, also known as risk minimization: the Bayes decision rule and the Bayes risk. Generative and discriminative models. Read ISL, Section 4.4 (the first few pages). My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 7 (February 7): Gaussian discriminant analysis, including quadratic discriminant analysis (QDA) and linear discriminant analysis (LDA). Maximum likelihood estimation (MLE) of the parameters of a statistical model. Fitting an isotropic Gaussian distribution to sample points. Read ISL, Section 4.4 (all of it). Optional: Read (selectively) the Wikipedia page on maximum likelihood estimation . My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 8 (February 12): Eigenvectors, eigenvalues, and the eigendecomposition of a symmetric real matrix. The quadratic form and ellipsoidal isosurfaces as an intuitive way of understanding symmetric matrices. Application to anisotropic multivariate normal distributions. The covariance of random variables. Read Chuong Do's notes on the multivariate Gaussian distribution . My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 9 (February 14): MLE, QDA, and LDA revisited for anisotropic Gaussians. Read ISL, Sections 4.4 and 4.5. My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

February 19 is Presidents' Day.

Lecture 10 (February 21): Regression: fitting curves to data. The 3-choice menu of regression function + loss function + cost function. Least-squares linear regression as quadratic minimization. The design matrix, the normal equations, the pseudoinverse, and the hat matrix (projection matrix). Logistic regression; how to compute it with gradient descent or stochastic gradient descent. Read ISL, Sections 4–4.3. My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 11 (February 26): Newton's method and its application to logistic regression. LDA vs. logistic regression: advantages and disadvantages. ROC curves. Weighted least-squares regression. Least-squares polynomial regression. Read ISL, Sections 7.1, 9.3.3; ESL, Section 4.4.1. Optional: here is a fine short discussion of ROC curves —but skip the incoherent question at the top and jump straight to the answer. My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 12 (February 28): Statistical justifications for regression. The empirical distribution and empirical risk. How the principle of maximum likelihood motivates the cost functions for least-squares linear regression and logistic regression. The bias-variance decomposition; its relationship to underfitting and overfitting; its application to least-squares linear regression. Read ESL, Sections 2.6 and 2.9. Optional: Read the Wikipedia page on the bias-variance trade-off . My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 13 (March 4): Ridge regression: penalized least-squares regression for reduced overfitting. How the principle of maximum a posteriori (MAP) motivates the penalty term (aka Tikhonov regularization). Subset selection. Lasso: penalized least-squares regression for reduced overfitting and subset selection. Read ISL, Sections 6–6.1.2, the last part of 6.1.3 on validation, and 6.2–6.2.1; and ESL, Sections 3.4–3.4.3. Optional: This CrossValidated page on ridge regression is pretty interesting. My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 14 (March 6): Decision trees; algorithms for building them. Entropy and information gain. Read ISL, Sections 8–8.1. My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

The Midterm took place on Monday, March 11 at 6:30–8:00 PM in multiple rooms on campus. The midterm covers Lectures 1–13, the associated readings listed on the class web page, Homeworks 1–4, and discussion sections related to those topics.

Lecture 15 (March 13): More decision trees: decision tree regression; stopping early; pruning; multivariate splits. Ensemble learning, bagging (bootstrap aggregating), and random forests. Read ISL, Section 8.2. The animations I show in class are available in this directory . My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 16 (March 18): Kernels. Kernel ridge regression. The polynomial kernel. Kernel perceptrons. Kernel logistic regression. The Gaussian kernel. Optional: Read ISL, Section 9.3.2 and ESL, Sections 12.3–12.3.1 if you're curious about kernel SVM. My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 17 (March 20): Neural networks. Gradient descent and the backpropagation algorithm. Read ESL, Sections 11.3–11.4. Optional: Welch Labs' video tutorial Neural Networks Demystified on YouTube is quite good (note that they transpose some of the matrices from our representation). Also of special interest is this Javascript neural net demo that runs in your browser. Here's another derivation of backpropagation that some people have found helpful. My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

March 25–29 is Spring Recess.

Lecture 18 (April 1): The vanishing gradient problem. Rectified linear units (ReLUs). Backpropagation with softmax outputs and cross-entropy loss. Neuron biology: axons, dendrites, synapses, action potentials. Differences between traditional computational models and neuronal computational models. Optional: Try out some of the Javascript demos on this excellent web page —and if time permits, read the text too. The first four demos illustrate the neuron saturation problem and its fix with the logistic loss (cross-entropy) functions. The fifth demo gives you sliders so you can understand how softmax works. My lecture notes (PDF). Note: the material on neurobiology in the Lecture 18 notes was not covered by Prof. Sahai, so it is not in scope for the Final Exam. Prof. Anant Sahai's lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 19 (April 3): Heuristics for faster training. Heuristics for avoiding bad local minima. Heuristics to avoid overfitting. Convolutional neural networks. Neurology of retinal ganglion cells in the eye and simple and complex cells in the V1 visual cortex. Read ESL, Sections 11.5 and 11.7. Here is the video about Hubel and Wiesel's experiments on the feline V1 visual cortex . Here is Yann LeCun's video demonstrating LeNet5 . Optional: A fine paper on heuristics for better neural network learning is Yann LeCun, Leon Bottou, Genevieve B. Orr, and Klaus-Robert Müller, “Efficient BackProp,” in G. Orr and K.-R. Müller (Eds.), Neural Networks: Tricks of the Trade , Springer, 1998. Also of special interest is this Javascript convolutional neural net demo that runs in your browser. Some slides about the V1 visual cortex and ConvNets (PDF). My lecture notes (PDF). Note: the material on the visual cortex in the Lecture 19 notes was not covered by Prof. Sahai, so it is not in scope for the Final Exam. Prof. Anant Sahai's lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 20 (April 8): Unsupervised learning. Principal components analysis (PCA). Derivations from maximum likelihood estimation, maximizing the variance, and minimizing the sum of squared projection errors. Eigenfaces for face recognition. Read ISL, Sections 12–12.2 (if you have the first edition, Sections 10–10.2) and the Wikipedia page on Eigenface . Optional: Watch the video for Volker Blanz and Thomas Vetter's A Morphable Model for the Synthesis of 3D Faces . My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 21 (April 10): The singular value decomposition (SVD) and its application to PCA. Clustering: k -means clustering aka Lloyd's algorithm; k -medoids clustering; hierarchical clustering; greedy agglomerative clustering. Dendrograms. Read ISL, Section 12.4 (if you have the first edition, Section 10.3). My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 22 (April 15): The geometry of high-dimensional spaces. Random projection. The pseudoinverse and its relationship to the singular value decomposition. Optional: Mark Khoury, Counterintuitive Properties of High Dimensional Space . Optional: The Wikipedia page on the Moore–Penrose inverse . For reference: Sanjoy Dasgupta and Anupam Gupta, An Elementary Proof of a Theorem of Johnson and Lindenstrauss , Random Structures and Algorithms 22 (1)60–65, January 2003. My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 23 (April 17): Learning theory. Range spaces (aka set systems) and dichotomies. The shatter function and the Vapnik–Chervonenkis dimension. Read Andrew Ng's CS 229 lecture notes on learning theory . For reference: Thomas M. Cover, Geometrical and Statistical Properties of Systems of Linear Inequalities with Applications in Pattern Recognition , IEEE Transactions on Electronic Computers 14 (3):326–334, June 1965. My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 24 (April 22): AdaBoost, a boosting method for ensemble learning. Nearest neighbor classification and its relationship to the Bayes risk. Read ESL, Sections 10–10.5, and ISL, Section 2.2.3. For reference: Yoav Freund and Robert E. Schapire, A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting , Journal of Computer and System Sciences 55 (1):119–139, August 1997. Freund and Schapire's Gödel Prize citation and their ACM Paris Kanellakis Theory and Practice Award citation . For reference: Thomas M. Cover and Peter E. Hart, Nearest Neighbor Pattern Classification , IEEE Transactions on Information Theory 13 (1):21–27, January 1967. For reference: Evelyn Fix and J. L. Hodges Jr., Discriminatory Analysis---Nonparametric Discrimination: Consistency Properties , Report Number 4, Project Number 21-49-004, US Air Force School of Aviation Medicine, Randolph Field, Texas, 1951. See also This commentary on the Fix–Hodges paper . My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

Lecture 25 (April 24): The exhaustive algorithm for k -nearest neighbor queries. Speeding up nearest neighbor queries. Voronoi diagrams and point location. k -d trees. Application of nearest neighbor search to the problem of geolocalization : given a query photograph, determine where in the world it was taken. If I like machine learning, what other classes should I take? For reference: the best paper I know about how to implement a k -d tree is Sunil Arya and David M. Mount, Algorithms for Fast Vector Quantization , Data Compression Conference, pages 381–390, March 1993. For reference: the IM2GPS web page , which includes a link to the paper. My lecture notes (PDF). The lecture video . In case you don't have access to bCourses, here's a backup screencast (screen only).

The Final Exam took place on Friday, May 10, 3–6 PM .

Discussion Sections and Teaching Assistants

Sections begin to meet on January 23.

Some of our office hours are online or hybrid, especially during the first few weeks of the semester. To attend an online office hour, submit a ticket to the Online Office Hour Queue at https://oh.eecs189.org . this Zoom link . Please read the online office hour rules in this Piazza post .

Your Teaching Assistants are: Suchir Agarwal Samuel Alber Pierre Boyeau Charles Dove Lydia Ignatova Aryan Jain Ziye Ma Norman Mu Andrew Qin Sowmya Thanvantri Kevin Wang Zekai Wang Richard Wu Gavin Zhang

Office hours are listed in this Google calendar link .

Supported in part by the National Science Foundation under Awards CCF-0430065, CCF-0635381, IIS-0915462, CCF-1423560, and CCF-1909204, in part by a gift from the Okawa Foundation, and in part by an Alfred P. Sloan Research Fellowship.

CSCI 335: Machine Learning

RIT CS Department, Fall 2023 (Section 1) Instructor: Prof. Zanibbi

This week we will focus on the project and briefly touch on some additional topics in the Charniak text.

• Final Office Hours:
•     This Week:  Monday 3-5 (Zoom -- see discord), Tuesday 3:30-4:30 (in-person), Friday 11am-2pm (usual, Zoom + in-person)
•      Next Week (*Reading Day Only):  9am-10am, 11am-12pm, 1pm-4pm (in-person + Zoom)
• Assignment 4 (required)  is due Wednesday at 11:59pm. Let submission will close Mon Dec 11 at 11:59pm.
• (Optional) Assignment 5 (resubmission for *one* of A1/2/3 - hard deadline Mon Dec 11, 11:59pm) . Your final assignment grade will be based on A1-A4, whether or not you resubmit one of the earlier assignments (1/2/3).
• Final Project:   
•    Project presentations will be given during the exam, Friday Dec. 15, 1:30-4pm regular classroom (Slaughter Hall Rm. 2150) .
•    The final report, code, and rough work due the Sunday after (submit through MyCourses by Dec. 17, 11:59pm). 
• Please complete the course evaluation.   This will help improve future offerings of the course, particularly in sorting out what to keep, change, or replace in the course.

This week we will focus on the project and some additional topics from the Charniak text.

• The final quiz (Quiz 10) will be released on Wednesday, and will be due Thursday before class.
• Assignment 4 (required)  is due next week, Wednesday of Week 15 (Dec. 6th). 
• Assignment 5 (optional - hard deadline Mon Dec 11, 11:59pm) . This is not a new assignment, instead, students may resubmit one of Assignments 1-3. If five assignment (with the optional A1-3 resubmission) are submitted , the four highest assignment grades will be kept, otherwise your assignment grade will be based on A1-A4.
• Project Proposals will be returned this week.
• (Reminder) Final Project:   Project presentations during the exam (Dec. 15, 1:30-4pm). Final report, code, and rough work due the Sunday after (Dec. 17, 11:59pm). 
• *Please complete the course evaluation.   This will help improve future offerings of the course, particularly in sorting out what to keep, change, or replace in the course.

This week will finish up RNNs / LSTMs, and introduce sequence-to-sequence models.

• No Class on Thursday.   Enjoy the holiday.
• Assignment 4 will be released over the break, and will be due Friday. Dec 1st   after the holiday break.
• Project Proposals will be returned by Monday of next week.
•      (Reminder) Final Project:   Project presentations during the exam (Dec. 15, 1:30-4pm). Final report, code, and rough work due the Sunday after (Dec. 17, 11:59pm). 
• Reading:  Ch. 5 of Introduction to Deep Learning (Charniak)  -- on sequence-to-sequence models

Topics this week: recurrent neural networks, including Long-Short Term Memory (LSTM) models.

• Quiz 9 is  due Thursday at 11:59pm
• Assignment 4 will be released by Tuesday before the break, and will be due Friday. Dec 1st   after the holiday break.
• Assignment 5 will be optional, and due Fri Dec 8th.   Your lowest assignment grade will be dropped -- this means that each remaining assignment will be 12.5% of your final grade (rather than 10%).  
• Final Project:   Project presentations during the exam (Dec. 15, 1:30-4pm). Final report, code, and rough work due the Sunday after (Dec. 17, 11:59pm). 
• Reading:  Ch. 4 of Introduction to Deep Learning (Charniak)  -- on recurrent neural networks

We are continuing our discussion of language models and recurrent neural networks this week.

• Quiz 8  will be released Wednesday, and due Thursday before class (1pm)
• Project Proposals (Deadline extension): P roject proposal is due Sunday, Nov. 12th at 11:59pm (submit through MyCourses).
•     Late submission deadline is still Friday, Nov. 17th at 11:59.      
•     Review the   recommendations for completing the project  
•      Suggestions for using conda to run different research systems are provided in the #projects channel on discord.
• Assignment 4 will be released Monday of Week 12, and is due Sunday evening before Wk 13.

We are concluding our discussion of CNNs and starting on recurrent neural nets this week.

• Assignment 3: due Friday at 11:59pm **Make sure to check the updated documents and code (MyCourses)
•     Clarifications made for Q3, Q4, correction for bonus, and additional installation instructions/tools provided.
•     Additional details available in the #assignments and #systems-install channels on discord. 
• Quiz 6 will be released Wednesday, and due Thursday before class (1pm)
• Project Proposals (Update): P roject proposal is due next Friday (Nov. 10th) at 11:59pm (submit through MyCourses).
•      Reminder: check the  recommendations for completing the project successfully
•      Suggestions regarding use of conda for running different research systems provided in the #projects channel on discord.

We are continuing our discussion of CNNs (convolutional neural networks) this week.

• Assignment 3: out Thursday , due next Friday at 11:59pm (Nov 3) 
• Project Proposals (Update): P roject proposal is due Friday Nov. 10th at 11:59pm (submit through MyCourses).
•     Consult  the documents on the proposal and final project in MyCourses, 
•      including the  recommendations for completing the project successfully .
• Reading:  Ch. 3 of Introduction to Deep Learning (Charniak)  -- on convolutional neural networks
• The course schedule has been updated (see link above).
• The syllabus has been updated regarding contacting the instructor on day that items are due (see link above).

We are continuing our discussion of Deep Neural Networks and their implementation this week.

• Quiz 5 will be released by Friday.
• Project Proposal Due Tues, Nov. 6:  Students need to select groups by this Friday in MyCourses. Project materials are online in MyCourses. 

There is no class on Tuesday -- enjoy the break.   On Thursday we will continue our discussion of implementing a single-layer neural net for MNIST classification in TensorFlow (see lecture slides for additional information on using TensorFlow).

• Reading:  Ch. 2 of Introduction to Deep Learning (Charniak) 
• Assignment 3 will be released this week
• Quiz 4 has been released, and is due Saturday at 12pm.
• Project: Start thinking about forming your group for the project. The project will be released in Week 8, and students will need to select groups by Friday of Wk 8 (students without a group will be randomly assigned by the MyCourses shell)
• Lectures:   **No Class on Tuesday**

This week we are concerned with training feed-forward neural networks using backpropagation, and its implementation using TensorFlow.

• Reading:  Read Ch. 2 of Introduction to Deep Learning (Charniak). 
• Assignment 2 is due Thursday (Oct 5th at 11:59pm) 
• We will have a quiz on Wednesday, due 1 hr before class.
• Lectures:    An additional video lecture on Bayesian classification using Gaussian density functions (see under Zoom 'Cloud recordings') was posted Monday. Some suggestions related to A2 are also provided in the video (and in the #assignment channel on the course discord).

This week we are starting to work on neural networks, and specifically feed-forward networks and the backpropagation algorithm used to fit their model weights.

• **Office Hours Change this Week.**   Office hours will be Friday from 10am-10:45am, and then from 12:30pm-2:30pm (this week only, due to a conflict).
• Reading:  Read Ch. 1 of Introduction to Deep Learning (Charniak). 
• Assignment 2 has been posted, and is due next week (Thurs Oct 5th at 11:59pm) 
• There is no quiz this week. Best of luck with the career fair!
• Lectures: Update:   The missed lecture from last week (on Bayesian classification, and a bit on Assignment 2) will be posted by Wednesday evening.

This week we will continue our discussion of Bayesian Decision Theory, along with approximated Bayes' models using gaussian functions for the probability density function in each class.

• Reading:  Read the probability and language model review from Charniak's Statistical Language Learning Ch. 2, and the introduction to Bayesian Decision Theory for classification in Duin et al.'s  Classification, Parameter Estimation, and State Estimation  (also Ch. 2). Both are well-written and reader-friendly. They are also available through MyCourses.
• Quiz 2  will be released Wednesday afternoon, and will be due at 1pm (1 hr before class) on Thursday.  Note:  Answers to Quiz 1 have been posted on MyCourses.
• Lectures: The missed lecture from last week will be posted over the weekend, before Monday of next week. This will provide  an opportunity to finish and review topics from our study of Bayesian Decision Theory.
• Assignment 2 will be released by Monday of next week.

**Lecture is cancelled Tuesday (Prof. Zanibbi away); the missed lecture will be posted as a video on MyCourses later this week.**

• Assignment 1   is due Thursday ( Sept. 14 ) at 11:59pm through MyCourses. Late submissions will be accepted up to one week later, with a 10% penalty and a possible delay in return of the grade.

Welcome to Week 2. Announcements will continue to be posted here throughout the semester.

• Reading:  Read the Hastie book, Ch. 1, and Ch. 2.1-2.3. This is available through MyCourses.
• Assignment 1   has been posted in MyCourses. It is due next Thursday ( Sept. 14 ) at 11:59pm through MyCourses. Late submissions will be accepted up to one week later, with a 10% penalty and a possible delay in return of the grade.
• Quiz 1 will be released Wednesday afternoon, and will be due at 1pm (1 hr before class) on Thursday.
• Lecture for Tuesday of Wk 3   is cancelled (Sept 12, No Class). This missed lecture will be posted as a video in MyCourses.

Welcome to the Fall 2023 (Section 1) Machine Learning course web pages.  These web pages will be used to communicate information about the course, along with news, deadlines, etc. 

• Prof. Zanibbi is the course instructor.
• The course syllabus and schedule are available . The schedule may change during the semester, and changes will be announced here and in-class. Use the links above to see the schedule and syllabus.
• Lectures:   Tuesdays and Thursdays in SLA-2150 (Slaughter Building, Building 78)
• Lectures will be given in-person and live over Zoom. Lecture attendance is strongly recommended; students will be tested on additional material discussed in lecture. 
• Deliverables: A description and grade weight for course deliverables can be found below.
• Quizzes, assignments and projects are distributed and submitted using MyCourses.

Grade Components

• Quizzes (10%)
• Assignments (50%)
• Project Proposal (15%)
• Final Project (25%)

10 quizzes will be given out weekly beginning in Week 2 of the semester. The two lowest quiz grades will be dropped. Quizzes will be available through a "Quizzes" link in MyCourses. Students are permitted to retake a quiz as many times as they like, and will receive the highest score that they receive across these attempts before the deadline. Students will have at least one day (24 hrs) to complete each quiz.

5 assignments  will be given, beginning in Week 3 of the semester. Assignments involve both writing and programming questions. Students are expected to follow submission instructions as provided in the assignments carefully. 

Instead of an exam, students will complete a group project at the end of the semester in groups of 3 students. The project involves designing, executing, and reporting on an experiment with a machine learning model. The first deliverable for the project is an experiment design, and a draft of the final experiment report and materials to be delivered for the final project.

Instead of an exam, students will complete a group project at the end of the semester in groups of 3 students. The project involves designing, executing, and reporting on an experiment with a machine learning model. The final deliverable for the project are the experimental results, code, and experiment report  (20%), along with a short 5-10 minute presentation given during the exam slot (5%). 

CSCI 335 Machine Learning, Fall 2023 RIT Department of Computer Science

Machine Learning And Deep Learning - Fundamentals And Applications

Note: This exam date is subjected to change based on seat availability. You can check final exam date on your hall ticket.

Page Visits

Course layout, books and references, instructor bio.

Prof. M. K. Bhuyan

• Professor, Department of Electronics & Electrical Engineering, IIT Guwahati, Assam, INDIA, 
• Dean of Infrastructure Planning and Management (IPM), IIT Guwahati, Assam, INDIA, 
• Visiting Professor, Department of Computer Science, Chubu University, JAPAN.
• Fulbright Scholar.

Course certificate

DOWNLOAD APP

SWAYAM SUPPORT

Please choose the SWAYAM National Coordinator for support. * :