Normal Hypothesis Testing ( AQA A Level Maths: Statistics )
Revision note.


Normal Hypothesis Testing
How is a hypothesis test carried out with the normal distribution.
- The population mean is tested by looking at the mean of a sample taken from the population
- A hypothesis test is used when the value of the assumed population mean is questioned
- Make sure you clearly define µ before writing the hypotheses, if it has not been defined in the question
- The null hypothesis will always be H 0 : µ = ...
- The alternative hypothesis will depend on if it is a one-tailed or two-tailed test
- The alternative hypothesis, H 1 will be H 1 : µ > ... or H 1 : µ < ...
- The alternative hypothesis, H 1 will be H 1 : µ ≠ ..
- Remember that the variance of the sample mean distribution will be the variance of the population distribution divided by n
- the mean of the sample mean distribution will be the same as the mean of the population distribution
- The normal distribution will be used to calculate the probability of the observed value of the test statistic taking the observed value or a more extreme value
- either calculating the probability of the test statistic taking the observed or a more extreme value ( p – value ) and comparing this with the significance level
- Finding the critical region can be more useful for considering more than one observed value or for further testing
How is the critical value found in a hypothesis test for the mean of a normal distribution?
- The probability of the observed value being within the critical region, given a true null hypothesis will be the same as the significance level
- To find the critical value(s) find the distribution of the sample means, assuming H 0 is true, and use the inverse normal function on your calculator
- For a two-tailed test you will need to find both critical values, one at each end of the distribution
What steps should I follow when carrying out a hypothesis test for the mean of a normal distribution?
- Following these steps will help when carrying out a hypothesis test for the mean of a normal distribution:
Step 2. Write the null and alternative hypotheses clearly using the form
H 0 : μ = ...
H 1 : μ ... ...
Step 4. Calculate either the critical value(s) or the p – value (probability of the observed value) for the test
Step 5. Compare the observed value of the test statistic with the critical value(s) or the p - value with the significance level
Step 6. Decide whether there is enough evidence to reject H 0 or whether it has to be accepted
Step 7. Write a conclusion in context
Worked example

You've read 0 of your 10 free revision notes
Get unlimited access.
to absolutely everything:
- Downloadable PDFs
- Unlimited Revision Notes
- Topic Questions
- Past Papers
- Model Answers
- Videos (Maths and Science)
Join the 100,000 + Students that ❤️ Save My Exams
the (exam) results speak for themselves:
Did this page help you?
Author: Amber
Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.
Hypothesis Testing with the Normal Distribution
Contents Toggle Main Menu 1 Introduction 2 Test for Population Mean 3 Worked Example 3.1 Video Example 4 Approximation to the Binomial Distribution 5 Worked Example 6 Comparing Two Means 7 Workbooks 8 See Also
Introduction
When constructing a confidence interval with the standard normal distribution, these are the most important values that will be needed.
Significance Level | $10$% | $5$% | $1$% |
|---|---|---|---|
$z_{1-\alpha}$ | $1.28$ | $1.645$ | $2.33$ |
$z_{1-\frac{\alpha}{2} }$ | $1.645$ | $1.96$ | $2.58$ |
Distribution of Sample Means
where $\mu$ is the true mean and $\mu_0$ is the current accepted population mean. Draw samples of size $n$ from the population. When $n$ is large enough and the null hypothesis is true the sample means often follow a normal distribution with mean $\mu_0$ and standard deviation $\frac{\sigma}{\sqrt{n}}$. This is called the distribution of sample means and can be denoted by $\bar{X} \sim \mathrm{N}\left(\mu_0, \frac{\sigma}{\sqrt{n}}\right)$. This follows from the central limit theorem .
The $z$-score will this time be obtained with the formula \[Z = \dfrac{\bar{X} - \mu_0}{\frac{\sigma}{\sqrt{n}}}.\]
So if $\mu = \mu_0, X \sim \mathrm{N}\left(\mu_0, \frac{\sigma}{\sqrt{n}}\right)$ and $ Z \sim \mathrm{N}(0,1)$.
The alternative hypothesis will then take one of the following forms: depending on what we are testing.
Worked Example
An automobile company is looking for fuel additives that might increase gas mileage. Without additives, their cars are known to average $25$ mpg (miles per gallons) with a standard deviation of $2.4$ mpg on a road trip from London to Edinburgh. The company now asks whether a particular new additive increases this value. In a study, thirty cars are sent on a road trip from London to Edinburgh. Suppose it turns out that the thirty cars averaged $\overline{x}=25.5$ mpg with the additive. Can we conclude from this result that the additive is effective?
We are asked to show if the new additive increases the mean miles per gallon. The current mean $\mu = 25$ so the null hypothesis will be that nothing changes. The alternative hypothesis will be that $\mu > 25$ because this is what we have been asked to test.
\begin{align} &H_0:\mu=25. \\ &H_1:\mu>25. \end{align}
Now we need to calculate the test statistic. We start with the assumption the normal distribution is still valid. This is because the null hypothesis states there is no change in $\mu$. Thus, as the value $\sigma=2.4$ mpg is known, we perform a hypothesis test with the standard normal distribution. So the test statistic will be a $z$ score. We compute the $z$ score using the formula \[z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n} } }.\] So \begin{align} z&=\frac{\overline{x}-25}{\frac{2.4}{\sqrt{30} } }\\ &=1.14 \end{align}
We are using a $5$% significance level and a (right-sided) one-tailed test, so $\alpha=0.05$ so from the tables we obtain $z_{1-\alpha} = 1.645$ is our test statistic.
As $1.14<1.645$, the test statistic is not in the critical region so we cannot reject $H_0$. Thus, the observed sample mean $\overline{x}=25.5$ is consistent with the hypothesis $H_0:\mu=25$ on a $5$% significance level.
Video Example
In this video, Dr Lee Fawcett explains how to conduct a hypothesis test for the mean of a single distribution whose variance is known, using a one-sample z-test.
Approximation to the Binomial Distribution
A supermarket has come under scrutiny after a number of complaints that its carrier bags fall apart when the load they carry is $5$kg. Out of a random sample of $200$ bags, $185$ do not tear when carrying a load of $5$kg. Can the supermarket claim at a $5$% significance level that more that $90$% of the bags will not fall apart?
Let $X$ represent the number of carrier bags which can hold a load of $5$kg. Then $X \sim \mathrm{Bin}(200,p)$ and \begin{align}H_0&: p = 0.9 \\ H_1&: p > 0.9 \end{align}
We need to calculate the mean $\mu$ and variance $\sigma ^2$.
\[\mu = np = 200 \times 0.9 = 180\text{.}\] \[\sigma ^2= np(1-p) = 18\text{.}\]
Using the normal approximation to the binomial distribution we obtain $Y \sim \mathrm{N}(180, 18)$.
\[\mathrm{P}[X \geq 185] = \mathrm{P}\left[Z \geq \dfrac{184.5 - 180}{4.2426} \right] = \mathrm{P}\left[Z \geq 1.0607\right] \text{.}\]
Because we are using a one-tailed test at a $5$% significance level, we obtain the critical value $Z=1.645$. Now $1.0607 < 1.645$ so we cannot accept the alternative hypothesis. It is not true that over $90$% of the supermarket's carrier bags are capable of withstanding a load of $5$kg.
Comparing Two Means
When we test hypotheses with two means, we will look at the difference $\mu_1 - \mu_2$. The null hypothesis will be of the form
where $a$ is a constant. Often $a=0$ is used to test if the two means are the same. Given two continuous random variables $X_1$ and $X_2$ with means $\mu_1$ and $\mu_2$ and variances $\frac{\sigma_1^2}{n_1}$ and $\frac{\sigma_2^2}{n_2}$ respectively \[\mathrm{E} [\bar{X_1} - \bar{X_2} ] = \mathrm{E} [\bar{X_1}] - \mathrm{E} [\bar{X_2}] = \mu_1 - \mu_2\] and \[\mathrm{Var}[\bar{X_1} - \bar{X_2}] = \mathrm{Var}[\bar{X_1}] - \mathrm{Var}[\bar{X_2}]=\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}\text{.}\] Note this last result, the difference of the variances is calculated by summing the variances.
We then obtain the $z$-score using the formula \[Z = \frac{(\bar{X_1}-\bar{X_2})-(\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}\text{.}\]
These workbooks produced by HELM are good revision aids, containing key points for revision and many worked examples.
- Tests concerning a single sample
- Tests concerning two samples
Selecting a Hypothesis Test
- The Open University
- Accessibility hub
- Guest user / Sign out
- Study with The Open University
My OpenLearn Profile
Personalise your OpenLearn profile, save your favourite content and get recognition for your learning
About this free course
Become an ou student, download this course, share this free course.

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.
4.1 The normal distribution
Here, you will look at the concept of normal distribution and the bell-shaped curve. The peak point (the top of the bell) represents the most probable occurrences, while other possible occurrences are distributed symmetrically around the peak point, creating a downward-sloping curve on either side of the peak point.
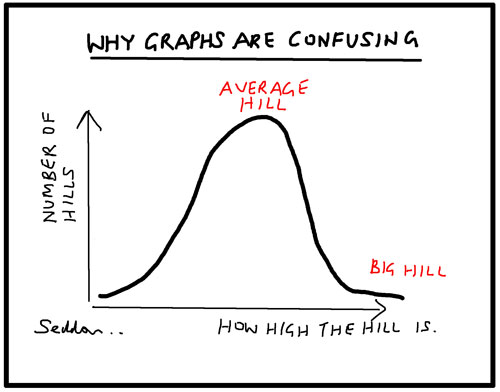
The cartoon shows a bell-shaped curve. The x-axis is titled ‘How high the hill is’ and the y-axis is titled ‘Number of hills’. The top of the bell-shaped curve is labelled ‘Average hill’, but on the lower right tail of the bell-shaped curve is labelled ‘Big hill’.
In order to test hypotheses, you need to calculate the test statistic and compare it with the value in the bell curve. This will be done by using the concept of ‘normal distribution’.
A normal distribution is a probability distribution that is symmetric about the mean, indicating that data near the mean are more likely to occur than data far from it. In graph form, a normal distribution appears as a bell curve. The values in the x-axis of the normal distribution graph represent the z-scores. The test statistic that you wish to use to test the set of hypotheses is the z-score . A z-score is used to measure how far the observation (sample mean) is from the 0 value of the bell curve (population mean). In statistics, this distance is measured by standard deviation. Therefore, when the z-score is equal to 2, the observation is 2 standard deviations away from the value 0 in the normal distribution curve.
A symmetrical graph reminiscent of a bell. The top of the bell-shaped curve appears where the x-axis is at 0. This is labelled as Normal distribution.
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Normal Distribution in Statistics
By Jim Frost 181 Comments
The normal distribution, also known as the Gaussian distribution, is the most important probability distribution in statistics for independent, random variables. Most people recognize its familiar bell-shaped curve in statistical reports.
The normal distribution is a continuous probability distribution that is symmetrical around its mean, most of the observations cluster around the central peak, and the probabilities for values further away from the mean taper off equally in both directions. Extreme values in both tails of the distribution are similarly unlikely. While the normal distribution is symmetrical, not all symmetrical distributions are normal. For example, the Student’s t, Cauchy, and logistic distributions are symmetric.
As with any probability distribution, the normal distribution describes how the values of a variable are distributed. It is the most important probability distribution in statistics because it accurately describes the distribution of values for many natural phenomena. Characteristics that are the sum of many independent processes frequently follow normal distributions. For example, heights, blood pressure, measurement error, and IQ scores follow the normal distribution.
In this blog post, learn how to use the normal distribution, about its parameters, the Empirical Rule, and how to calculate Z-scores to standardize your data and find probabilities.
Example of Normally Distributed Data: Heights
Height data are normally distributed. The distribution in this example fits real data that I collected from 14-year-old girls during a study. The graph below displays the probability distribution function for this normal distribution. Learn more about Probability Density Functions .

As you can see, the distribution of heights follows the typical bell curve pattern for all normal distributions. Most girls are close to the average (1.512 meters). Small differences between an individual’s height and the mean occur more frequently than substantial deviations from the mean. The standard deviation is 0.0741m, which indicates the typical distance that individual girls tend to fall from mean height.
The distribution is symmetric. The number of girls shorter than average equals the number of girls taller than average. In both tails of the distribution, extremely short girls occur as infrequently as extremely tall girls.
Parameters of the Normal Distribution
As with any probability distribution, the parameters for the normal distribution define its shape and probabilities entirely. The normal distribution has two parameters, the mean and standard deviation. The Gaussian distribution does not have just one form. Instead, the shape changes based on the parameter values, as shown in the graphs below.
The mean is the central tendency of the normal distribution. It defines the location of the peak for the bell curve. Most values cluster around the mean. On a graph, changing the mean shifts the entire curve left or right on the X-axis. Statisticians denote the population mean using μ (mu).
μ is the expected value of the normal distribution. Learn more about Expected Values: Definition, Using & Example .

Related posts : Measures of Central Tendency and What is the Mean?
Standard deviation σ
The standard deviation is a measure of variability. It defines the width of the normal distribution. The standard deviation determines how far away from the mean the values tend to fall. It represents the typical distance between the observations and the average. Statisticians denote the population standard deviation using σ (sigma).
On a graph, changing the standard deviation either tightens or spreads out the width of the distribution along the X-axis. Larger standard deviations produce wider distributions.

When you have narrow distributions, the probabilities are higher that values won’t fall far from the mean. As you increase the spread of the bell curve, the likelihood that observations will be further away from the mean also increases.
Related post : Measures of Variability and Standard Deviation
Population parameters versus sample estimates
The mean and standard deviation are parameter values that apply to entire populations. For the Gaussian distribution, statisticians signify the parameters by using the Greek symbol μ (mu) for the population mean and σ (sigma) for the population standard deviation.
Unfortunately, population parameters are usually unknown because it’s generally impossible to measure an entire population. However, you can use random samples to calculate estimates of these parameters. Statisticians represent sample estimates of these parameters using x̅ for the sample mean and s for the sample standard deviation.
Learn more about Parameters vs Statistics: Examples & Differences .
Common Properties for All Forms of the Normal Distribution
Despite the different shapes, all forms of the normal distribution have the following characteristic properties.
- They’re all unimodal , symmetric bell curves. The Gaussian distribution cannot model skewed distributions.
- The mean, median, and mode are all equal.
- Half of the population is less than the mean and half is greater than the mean.
- The Empirical Rule allows you to determine the proportion of values that fall within certain distances from the mean. More on this below!
While the normal distribution is essential in statistics, it is just one of many probability distributions, and it does not fit all populations. To learn how to determine whether the normal distribution provides the best fit to your sample data, read my posts about How to Identify the Distribution of Your Data and Assessing Normality: Histograms vs. Normal Probability Plots .
The uniform distribution also models symmetric, continuous data, but all equal-sized ranges in this distribution have the same probability, which differs from the normal distribution.
If you have continuous data that are skewed, you’ll need to use a different distribution, such as the Weibull , lognormal , exponential , or gamma distribution.
Related post : Skewed Distributions
The Empirical Rule for the Normal Distribution
When you have normally distributed data, the standard deviation becomes particularly valuable. You can use it to determine the proportion of the values that fall within a specified number of standard deviations from the mean. For example, in a normal distribution, 68% of the observations fall within +/- 1 standard deviation from the mean. This property is part of the Empirical Rule, which describes the percentage of the data that fall within specific numbers of standard deviations from the mean for bell-shaped curves.
| 1 | 68% |
| 2 | 95% |
| 3 | 99.7% |
Let’s look at a pizza delivery example. Assume that a pizza restaurant has a mean delivery time of 30 minutes and a standard deviation of 5 minutes. Using the Empirical Rule, we can determine that 68% of the delivery times are between 25-35 minutes (30 +/- 5), 95% are between 20-40 minutes (30 +/- 2*5), and 99.7% are between 15-45 minutes (30 +/-3*5). The chart below illustrates this property graphically.

If your data do not follow the Gaussian distribution and you want an easy method to determine proportions for various standard deviations, use Chebyshev’s Theorem ! That method provides a similar type of result as the Empirical Rule but for non-normal data.
To learn more about this rule, read my post, Empirical Rule: Definition, Formula, and Uses .
Standard Normal Distribution and Standard Scores
As we’ve seen above, the normal distribution has many different shapes depending on the parameter values. However, the standard normal distribution is a special case of the normal distribution where the mean is zero and the standard deviation is 1. This distribution is also known as the Z-distribution.
A value on the standard normal distribution is known as a standard score or a Z-score. A standard score represents the number of standard deviations above or below the mean that a specific observation falls. For example, a standard score of 1.5 indicates that the observation is 1.5 standard deviations above the mean. On the other hand, a negative score represents a value below the average. The mean has a Z-score of 0.

Suppose you weigh an apple and it weighs 110 grams. There’s no way to tell from the weight alone how this apple compares to other apples. However, as you’ll see, after you calculate its Z-score, you know where it falls relative to other apples.
Learn how the Z Test uses Z-scores and the standard normal distribution to determine statistical significance.
Standardization: How to Calculate Z-scores
Standard scores are a great way to understand where a specific observation falls relative to the entire normal distribution. They also allow you to take observations drawn from normally distributed populations that have different means and standard deviations and place them on a standard scale. This standard scale enables you to compare observations that would otherwise be difficult.
This process is called standardization, and it allows you to compare observations and calculate probabilities across different populations. In other words, it permits you to compare apples to oranges. Isn’t statistics great!
To standardize your data, you need to convert the raw measurements into Z-scores.
To calculate the standard score for an observation, take the raw measurement, subtract the mean, and divide by the standard deviation. Mathematically, the formula for that process is the following:
X represents the raw value of the measurement of interest. Mu and sigma represent the parameters for the population from which the observation was drawn.
After you standardize your data, you can place them within the standard normal distribution. In this manner, standardization allows you to compare different types of observations based on where each observation falls within its own distribution.
Example of Using Standard Scores to Make an Apples to Oranges Comparison
Suppose we literally want to compare apples to oranges. Specifically, let’s compare their weights. Imagine that we have an apple that weighs 110 grams and an orange that weighs 100 grams.
If we compare the raw values, it’s easy to see that the apple weighs more than the orange. However, let’s compare their standard scores. To do this, we’ll need to know the properties of the weight distributions for apples and oranges. Assume that the weights of apples and oranges follow a normal distribution with the following parameter values:
| Mean weight grams | 100 | 140 |
| Standard Deviation | 15 | 25 |
Now we’ll calculate the Z-scores:
- Apple = (110-100) / 15 = 0.667
- Orange = (100-140) / 25 = -1.6
The Z-score for the apple (0.667) is positive, which means that our apple weighs more than the average apple. It’s not an extreme value by any means, but it is above average for apples. On the other hand, the orange has fairly negative Z-score (-1.6). It’s pretty far below the mean weight for oranges. I’ve placed these Z-values in the standard normal distribution below.

While our apple weighs more than our orange, we are comparing a somewhat heavier than average apple to a downright puny orange! Using Z-scores, we’ve learned how each fruit fits within its own bell curve and how they compare to each other.
For more detail about z-scores, read my post, Z-score: Definition, Formula, and Uses
Finding Areas Under the Curve of a Normal Distribution
The normal distribution is a probability distribution. As with any probability distribution, the proportion of the area that falls under the curve between two points on a probability distribution plot indicates the probability that a value will fall within that interval. To learn more about this property, read my post about Understanding Probability Distributions .
Typically, I use statistical software to find areas under the curve. However, when you’re working with the normal distribution and convert values to standard scores, you can calculate areas by looking up Z-scores in a Standard Normal Distribution Table.
Because there are an infinite number of different Gaussian distributions, publishers can’t print a table for each distribution. However, you can transform the values from any normal distribution into Z-scores, and then use a table of standard scores to calculate probabilities.
Using a Table of Z-scores
Let’s take the Z-score for our apple (0.667) and use it to determine its weight percentile. A percentile is the proportion of a population that falls below a specific value. Consequently, to determine the percentile, we need to find the area that corresponds to the range of Z-scores that are less than 0.667. In the portion of the table below, the closest Z-score to ours is 0.65, which we’ll use.

Click here for a full Z-table and illustrated instructions for using it !
The trick with these tables is to use the values in conjunction with the properties of the bell curve to calculate the probability that you need. The table value indicates that the area of the curve between -0.65 and +0.65 is 48.43%. However, that’s not what we want to know. We want the area that is less than a Z-score of 0.65.
We know that the two halves of the normal distribution are mirror images of each other. So, if the area for the interval from -0.65 and +0.65 is 48.43%, then the range from 0 to +0.65 must be half of that: 48.43/2 = 24.215%. Additionally, we know that the area for all scores less than zero is half (50%) of the distribution.
Therefore, the area for all scores up to 0.65 = 50% + 24.215% = 74.215%
Our apple is at approximately the 74 th percentile.
Below is a probability distribution plot produced by statistical software that shows the same percentile along with a graphical representation of the corresponding area under the bell curve. The value is slightly different because we used a Z-score of 0.65 from the table while the software uses the more precise value of 0.667.

Related post : Percentiles: Interpretations and Calculations
Other Reasons Why the Normal Distribution is Important
In addition to all of the above, there are several other reasons why the normal distribution is crucial in statistics.
- Some statistical hypothesis tests assume that the data follow a bell curve. However, as I explain in my post about parametric and nonparametric tests , there’s more to it than only whether the data are normally distributed.
- Linear and nonlinear regression both assume that the residuals follow a Gaussian distribution. Learn more in my post about assessing residual plots .
- The central limit theorem states that as the sample size increases, the sampling distribution of the mean follows a normal distribution even when the underlying distribution of the original variable is non-normal.
That was quite a bit about the bell curve! Hopefully, you can understand that it is crucial because of the many ways that analysts use it.
If you’re learning about statistics and like the approach I use in my blog, check out my Introduction to Statistics book! It’s available at Amazon and other retailers.

Share this:

Reader Interactions
January 17, 2023 at 8:55 am
Thanks Jim for the detailed response. much appreciated.. it makes sense.
January 16, 2023 at 7:20 pm
Hi Jim, well, one caveat to your caveat. 🙂 I am assuming that even though we know the general mean is 100, that we do NOT know if there is something inherent about the two schools whereby their mean might not represent the general population, in fact I made it extreme to show that their respective means are probably NOT 100.. So, for the school with an IQ of 60, maybe it is 100, maybe it is 80, maybe it is 60, maybe it is 50, etc. But it seems to me that we could do a probability distribution around each of those in some way. (i.e what if their real mean was 100, what is the sampling distribution, what if the real mean is 80, what is the samplind distribution, etc.) So, I guess ultimately, I am asking two things. 1) what is the real mean for the school with a mean of 60 (in the case of the lower scoring school-intuition tells me it must be higher), but the second question then is, and perhaps the real crux of my question is how would we go about estimating those respective means. To me, this has Bayesian written all over it (the prior is 100, the updated info is 60, etc). But I only know Bayes with probabilities. anyway, I think this is an important question with bayesian thinking needed, and I dont think this subject gets the attention it deserves. I much appreciate your time, Jim. Hopefully a hat trick (3rd response) will finish this up. 🙂 — and hopefully your readers get something from this. Thanks John
January 16, 2023 at 11:08 pm
I explicitly mentioned that as an assumption in my previous comment. The schools need to represent the general population in terms of its IQ score distribution. Yes, it’s possible that the schools represent a different population. In that case, the probabilities don’t apply AND you wouldn’t even know whether the subsequent sample mean was likely to be higher or lower. You’d need to do a bit investigation to determine whether the school represented the general population or some other population. That’s exactly why I mentioned that. And my answer was based on you wanting to use the outside knowledge of the population.
Now, if you don’t want to assume that the general population’s IQ distribution is a normal distribution with a mean of 100 and standard deviation of 15, then you’re back to what I was writing about in my previous comment where you don’t use that information. In short, if you want to know the school’s true mean IQ, you’ll need to treat it as your population. Then draw a good sized random sample from it. Or, if the school is small enough, assess the entire school. As it is, you only have a sample size of 5. That’s not going to give you a precise estimate. You’d check the confidence interval for that estimate to see a range of likely values for the school’s mean.
You could use a Bayesian approach. That’s not my forte. But if you did draw a random sample of 5 and got a mean IQ of 60, that’s so unlikely to occur if the school’s mean is 100 that using a prior of 100 in a Bayesian analysis is questionable. That’s the problem with Bayesian approaches. You need priors, for which you don’t always have solid information. In your example, you’d need to know a lot more about the schools to have reasonable priors.
In this case, it seems likely that the schools mean IQ is not 100. It’s probably lower, but what is it. Hard to say. Seems like you’d need to really investigate the school to see what’s going on. Did you just get a really flukey sample, but the school does represent the general population. Or, does the school represent a different population?
Until you really looked in-depth at the school to get at that information, your best estimate is your sample mean along with the CI to understand its low precision.
January 16, 2023 at 9:54 am
Hi Jim, Thanks for response. I was assuming that we DO KNOW it has a general population mean of 100. I was also thinking in a Bayesian way that knowing the general population mean is 100, that the REAL Mean of the one school is BETWEEN 60 and 100 and the REAL mean of the other school is BETWEEN 100 and 140, much like if you were a baseball scout and you know that the average player is a .260 hitter, and you watch him bat 10 times, and get 8 hits, you would not assume his REAL ability is .800, you would assume it is BETWEEN .260 and .800 and perhaps use a Beta distribution, to conclude his distribution of averages is centered, at.. I don’t know, something like .265… something LARGER than .260. But this seems paradoxical to the idea that if we did get a sample of 5 (or however, many) and got a mean of 60 and in thinking of a confidence interval for that mean of 60, it is equally like that the REAL mean is say 55 as compared to 65.
January 16, 2023 at 6:50 pm
Gotcha! So, yes, using the knowledge outside our dataset, we can draw some additional conclusions.
For one thing, there’s regression to the mean. Usually that applies to one unusual observation being followed by an observation that is likely to be closer to the mean. In this case, we can use the same principle but apply it to samples of N = 5. You’ve got an unusual sample from each school. If you were to draw another random sample of the same size from each school, those samples are likely to be closer to the mean.
There are a few caveats. We’re assuming that we’re drawing random samples and that the schools reflect the general population rather than special populations.
As for getting the probability for N = 5 of the IQ sample mean equaling 60 or 140, we can use the sampling distribution as I mentioned. We need to find the probability of obtaining a random sample 140. The graph shows the sampling distribution below.
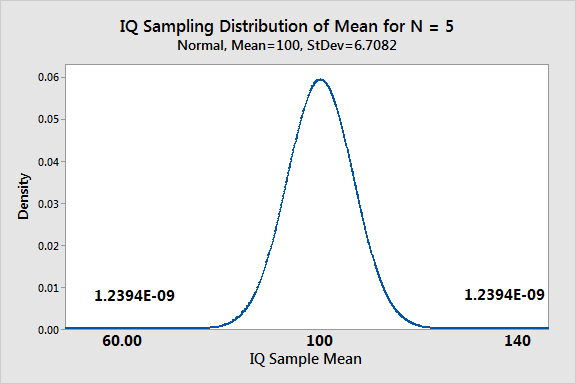
The probability for 140 is the same. Total probability getting either condition in one random sample is 0.0000000024788.
As you can see, either probability is quite low! Basically, don’t count on getting either sample mean under these conditions! Those sample means are just far out in the tails of the sampling distribution.
But, if you did get either of those means, what’s the probability that the next random sample of N = 5 will be closer to the true mean?
That probability equals: 1 – 0.0000000024788 = 0.9999999975212
It’s virtually guaranteed in this case that the next random sample of 5 will be closer to the correct mean!
January 13, 2023 at 8:11 am
Hi Jim, Thanks for these posts. I have a question related to the error term in a normal distribution. Let’s assume that we are taking IQs at various high schools. we go to one high school, take 5 IQ’s and the mean is 140. we go to another, take 5 IQS and the mean is 60. We are trying to determine the population mean at each school. Of course, We know that the 140 and 60 are just estimates of the respective high schools, is there some “boundedness” concept (seems intuitive) that would suggest that the real mean at the one school is more likely higher than 60 than lower, and the mean at the other school is more likely lower than 140 than higher. I am thinking of a probability density function of error terms about each of 60 and 140 would illustrate that. Can we confirm this mathematically? hope my question makes sense. Thanks John
January 13, 2023 at 11:54 pm
That’s kind of a complex question! In the real world, we know that IQs are defined as having a general population mean of 100. But let’s pretend we don’t know that.
I’ll assume that you randomly sampled the 5 students at both of the schools.
Going strictly by the data we gathered, it would be hard for us to know whether the overall HS population mean is between the two schools. It’s also possible that the two high schools have different means for reasons unknown to us. So, it’s really hard to draw conclusions. Particularly with only a measly 5 observations at two schools. There’s going to be a large margin of uncertainty with both estimates.
So, we’ll left in a situation where we don’t know what the overall population mean is, we don’t know if the two high schools should have different means or not, and the two estimates we have wide margins of error.
In short, we don’t know much! What we should do over time is build our knowledge in this area. Get large samples from those two schools and other schools. Try to identify reasons why the IQs might be different at various schools. Or find that they should be nearly identical. After we build up our knowledge, we can help that aid our understanding.
But with just 5 observations at two schools and ignoring our real-world knowledge, we couldn’t put much faith in the estimates of 60 and 140 and really not much reason to assume the 60 should be higher and the 140 lower.
Now, if you want to apply real-world knowledge that we do have, yes, we can be reasonably sure that the 60 is too low and the 140 is too high. It is inconceivable that any reasonably sized school would have either mean for the entire school population unless they were schools intended for special students. It is much more likely that those are fluky samples based on the tiny sample size. We can know all that because we know that the population average truly is 100 with a standard deviation of 15. Given that fact, you could look at the sampling distribution of the mean for each school’s size to determine the probability of having such an extreme mean IQ for the entire school.
But it wasn’t clear from your question if you wanted to incorporate that information or not. If you do, then what you need is the sampling distribution of the mean and use that to calculate the probability for each school. It won’t tell you for sure whether the means are too high or too low, but you’ll see how unlikely they are to occur given the known properties of the population, and you could conclude it’s more likely they’re just wrong–too low and too high!
December 2, 2022 at 2:44 pm
Hello. I’m new to this field and have a very basic question. If the average number of engine hours on a small aircraft between oil services is 29.9. And my SD is 14.1, does that mean 68.27% of all values lie between 44.0 (29.9+14.1) and 15.8 (29.9-14.1)?
December 2, 2022 at 5:12 pm
You do need to assume or know that the distribution in question follows a normal distribution. If it does, then, yes, your conclusions are absolutely correct!
In statistics classes, you’ll frequently have questions that state you can assume the data follow a normal distribution or that it’s been determined that they do. In the real world, you’ll need previous research to establish that. Or you might use it as a rough estimate if you’re not positive about normality but pretty sure the distribution is at least roughly normal.
So, there are a few caveats but yes, you’re understanding is correct.
June 27, 2022 at 1:38 pm
Hello, I have a question related to judgments regarding a population and the potential to identify a mixture distribution. I have a dataset which is not continuous – there is a significant gap between two groups of data. Approximately 98% of my data is described by one group and 2% of my data by another group. The CDF of all data looks like a mixture distribution; there is a sharp change in local slopes on either side of the non-continuous data range. I am using NDE methods to detect residual stress levels in pipes. My hypothesis is that discrete stress levels exist as a result of manufacturing methods. That is, you either have typical stress levels or you have atypical stress levels. 1. Can the non-continuous nature of the data suggest a mixture distribution? 2. What test(s) can be performed to establish that the two sub-groups are not statistically compatible?
December 20, 2021 at 10:10 am
Thanks for how to identify what distribution to use. I was condused at first I have understoot in normal, it is continuous and w ecan see on the X -axis the SD line is not clossed on it. In the Poison, it is a discreet thus with a time frame/linit. In Binomial, the outcome expected is post/neg, yes/no, gfalse/true etc. Thus two outcomes.
I can also say that in normal , there is complexity in random variables to be used.
December 21, 2021 at 1:03 am
Hi Evalyne,
I’m not sure that I understand what your question is. Yes, normal distributions require continuous data. However, not all continuous data follow a normal distribution.
Poisson distributions use discrete data–specifically count data. Other types of discrete data do not follow the Poisson distribution. For more information, read about the Poisson distribution .
Binomial distributions model the expected outcomes for binary data. Read more about the binomial distribution .
December 20, 2021 at 10:00 am
Thanks Jim Frost for your resource. I am learning this and has added alot to my knowledge.
November 15, 2021 at 2:44 pm
Thanks for your explanations, they are very helpful
October 5, 2021 at 4:21 am
Interesting. I Need help. Lets say I have 5 columns A B C D E
A follows Poisson Distribution B follows Binomial Distribution C follows Weibull Distribution D follows Negative Binomial Distribution E follows Exponential Distribution
Alright now I know what type of distribution my data follows, Then What should I do next ? How can this help me in exploratory data analysis ,in decision making or in machine learning ?
What if I don’t know what type of distribution my data follows because they all look confusing or similar when plotting it. Is there any equation can help ? is there libraries help me identifies the probability distribution of the data ?
Kindly help
October 7, 2021 at 11:50 pm
Hi Savitur,
There are distribution tests that will help you identify the distribution that best fits your data. To learn how to do that, read my post about How to Identify the Distribution of Your Data .
After you know the distribution, you can use it to make better predictions, estimate probabilities and percentiles, etc.
June 17, 2021 at 2:25 pm
Jim, Simple question. I am working on a regression analysis to determine which of many variables predict success in nursing courses. I had hoped to use one cohort, but realize now that I need to use several to perform an adequate analysis. I worry that historic effects will bias the scores of different cohorts. I believe that using z-scores (using the mean and SD to normalize each course grade for each cohort) will attenuate these effects. Am I on the right track here?
June 19, 2021 at 4:11 pm
Keep in mind that for regression, it’s not the distribution of IVs that matter so much. Technically, it’s the distribution of the residuals. However, if the DV is highly skewed it can be more difficult to obtain normal residuals. For more information, read my post about OLS Assumptions .
If I understand correctly, you want to use Z-scores to transform your data so it is normal. Z-scores won’t work for that. There are types of transformations for doing what you need. I write about those in my regression analysis book .
Typically, you’d fit the model and see if you have problematic residuals before attempting a transformation or other type of solution.
March 1, 2021 at 11:28 pm
I have a question: why in linear models follow the normal distribution, but in generalized linear models (GLM) follow the exponential distribution? I want a detailed answer to a question
March 2, 2021 at 2:43 am
Hi S, the assumptions for any analysis depend on the calculations involved. When an analysis makes an assumption about the distribution of values, it’s usually because of the probability distribution that the assumption uses to determine statistical significance. Linear models determine significance because they use the t-distribution for individual continuous predictors and F-distribution for groups of indicator variables related to a categorical variable. Both distributions assume that the sampling distribution of means follow the normal distribution. However, generalized linear models can use other distributions for determining significance. By the way, typically regression models make assumptions about the distribution of the residuals rather than the variables themselves.
I hope that helps.
February 13, 2021 at 3:06 am
thanks a lot Jim. Regards
February 12, 2021 at 10:41 pm
Thanks a lot for your valuable comments. My dependant variable is binary, I have proportions on which I am applying binominal glm. I would like to ask that if we get non normal residuals with such data and are not able to meet the assumptions of binomial glm that what is the alternative test? If not binomial glm then what?
February 12, 2021 at 6:38 am
I applied glm on my binomial data. Shapiro test on residuals revealed normal distribution however the same test with response variable shows non-normal distribution of response variable. What should I assume in this case? Can you please clarify?
I shall be highly thankful for your comments.
February 12, 2021 at 3:02 pm
Binary data (for the binomial distribution) cannot follow the normal distribution. So, I’m unsure what you’re asking about? Is your binary data perhaps an independent variable?
At any rate, the normality assumption, along with the other applicable assumptions apply to the residuals and not the variables in your model. Assess the normality of the residuals. I write about this in my posts about residual plots and OLS assumptions , which apply to GLM.
And, answering the question in your other comment, yes, it is possible to obtain normal residuals even when your dependent variable is nonnormal. However, if your DV is very skewed, that can make it more difficult to obtain normal residuals. However, I’ve obtain normal residuals when the DV was not normal. I discuss that in the post about OLS assumptions that I link to above.
If you have more specific questions after reading those posts, please don’t hesitate to comment in one of those posts.
I hope that helps!
February 12, 2021 at 3:26 am
Thanks for the answer, so I can conclude that only some (but not all) numerical data (interval or ratio) follow the normal distribution. The categorical data almost has a non-normal distribution. But regarding the ordinal data, aren’t they categorical type? Regards
February 12, 2021 at 3:13 pm
Yes, not all numeric data follow the normal distribution. If you want to see an example of nonnormal data, and how to determine which distribution data follow, read my post about identifying the distribution of your data , which is about continuous data.
There are also distribution tests for discrete data .
Categorical data CANNOT follow the normal distribution.
Ordinal data is its own type of data. Ordinal data have some properties of numeric data and some of categorical data, but it is neither.
I cover data types and related topics in my Introduction to Statistics book . You probably should consider it!
February 9, 2021 at 2:52 am
Hi I have a question about the categorical data. Should we consider the categorical data (i.e. Nominal and Ordinal ) that they almost have a non-normal distribution, and therefore they need nonparametric tests? Regards Jagar
February 11, 2021 at 4:52 pm
Categorical data are synonymous with nominal data. However, ordinal data is not equivalent to categorical data.
Categorical data cannot follow a normal distribution because your talking about categories with no distance or order between them. Ordinal data have an order but no distance. Consequently, ordinal data cannot be normally distributed. Only numeric data can follow a normal distribution.
February 6, 2021 at 9:24 am
What actually I was also trying to wonder about is whether there can be no deviation between the results from the data which has been transformed and the same sample data where we waived the normality assumption. Because now I know that with nonparametric tests, I first need to ascertain whether the the other measures of central tendency (mode and median) fit the subject matter of my research questions. Thank you Jim
February 6, 2021 at 11:39 pm
If you meet the sample size minimums, you can safely waive the normality assumption. The results should be consistent with a transformation assuming you use an appropriate transformation. If you don’t meet the minimum requirements for waiving the assumption, there might be differences.
Those sample size requirements are based on simulation studies that intentionally violated the normality assumption and then compared the actual to expected results for different sample sizes. The researchers ran the simulations thousands and thousands of times using different distributions and sample sizes. When you exceed the minimums, the results are reliable even when the data were not normally distributed.
February 6, 2021 at 2:53 am
That is a good idea! Yes, you definitely understand what I am trying to do and why it makes sense too – but of course only if the dimensions are truly independent and, as you say, it depends on them all following a normal distribution.
What I worry about your solution is what if other dimensions are not outliers? Imagine 10 dimensions and eight of them have a very low z-score only two have outlier z-score of 2.4
If we assume the remaining 8 dimensions are totally not outliers, such as z-score 0.7. That z-score has two tailed probability of 0.4839 if you take it power of eight it results of 0.003 probability and I worry it is not correct it seems very low in case we imagine such quite ordinary figures.
But maybe it is accurate, I cannot decide. In this case though the more features we add the more our probability drops.
Imagine you take a totally ordinary random sample in 50 degrees (fifty z-values). When you multiply them this way it will seem like your sample is extraordinarily rare outlier like p < 0.000005. Don't you agree?
So isn't this a problem if every sample looks like an extraordinarily rare outlier like p < 0.000005? I would expect actually 50% of samples to look like p < 0.5 and only less than 2% of samples to look like p < 0.02 …
So I am thinking there should be some better way to combine the z values other than multiplying result two tailed p. I thought about average of z values but for example imagine eight values of 0.5 and two values of 6. The sixes are major major outliers (imagine six sigma) and in two dimensions it takes the cake. So should be super rare. However if I average 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 6, 6 I get 1.6 sigma which seems very close to ordinary. It is not ordinary! Never I should get a sample which independently in two dimensions falls outside of six sigma. So also average is not good method here.
So I hope you see my dilemma through these examples. I think your method to multiply probabilities is powerful but is there any way to make it more powerful such that 50% of samples are p < 0.5 only?
Also I would not like to use manually picking which dimensions to consider as outliers and discard others, because it would be better somehow to combine all the scores in a way that is automatic and gets a resulting amount of outlier overall.
Overall I think your technique is pretty powerful I just worry little bit about using it in many dimensions. Thank you for the powerful tip!
February 7, 2021 at 12:01 am
I’m also split on this! Part of me says that is the correct answer. It does seem low. But imagine flipping a coin 8 times. The probability of getting heads all 8 times is extraordinarily low. The process is legitimate. And, if you have a number of medium scores and a few outliers, that should translate to a low probability. So, that doesn’t surprise me.
I can see the problem if you have many properties. You might look into the Mahalanobis distance. It measures the distances of data points form the centroid of a multivariate data set. Here’s the Wikipedia article about it: Mahalanobis distance . I’m familiar with it enough to know it might be what you’re looking for but I haven’t worked with it myself so I don’t have the hands on info!
February 5, 2021 at 10:12 pm
I want to know how unlikely the observation is overall, expressed as a single pvalue or overall z-score. Yes, the dimensions are truly independent. Is this possible?
February 6, 2021 at 12:19 am
Thanks for the extra details. I have a better sense of what you want to accomplish!
Typically, in the analyses I’m familiar with, analysts would assess each dimension separately, particularly if they’re independent. Basically checking for outliers based on different characteristics. However, it seems like you want a cumulative probability for unlikeliness that factors in both dimensions together. For example, if both dimensions were somewhat unusual, then the observation as a whole might be extremely unusual. I personally have never done anything like that.
However, I think I have an idea. I think you were thinking in the right direction when you mentioned p-values. If you use the Z-score to find the probability of obtaining each value, or more extreme, that is similar to similar to a p-value. So, if your Z-score was say 2.4, you’d find the probability for less than -2.4 and greater than +2.4. Sum those two probability of those two tails. Of course, obtaining accurate results depends on your data following a normal distribution.
You do that for both dimensions. For each observation, you end up with two probabilities.
Because these are independent dimensions, you can simply multiple the two probabilities for each observation to obtain the overall probability. I think that’ll work. Like I said, I haven’t done this myself but it seems like a valid approach.
February 5, 2021 at 6:37 pm
How can I combine several independent z-scores (different dimensions about the same item) into one overall z-score about how unlikely or percentile such an item is? Assuming the dimensions are truly independent of course.
February 5, 2021 at 9:55 pm
If the dimensions are truly independent, why do you want to combine them? Wouldn’t you want to capture the full information they provide?
February 5, 2021 at 12:51 am
Deciding between waiving the normality assumption and performing data transformation for none-normal data always gives headache when I have a sample size of n > 20.
I wonder how critical is the normality assumption vis-a- vis data transformation. Please help me tell me the appropriate decision I can take. Thank you
February 5, 2021 at 10:14 pm
Hi Collinz,
It can be fairly easy to waive the normality assumption. You really don’t need a very large sample size. In my post about parametric vs. nonparametric tests , I provide a table that shows the sample sizes per group for various analyses that allow you to waive that assumption. If you can waive the assumption, I would not transform the data as that makes the results less intuitive. So, check out that table and it should be an easy decision to make! Also, nonparametric tests are an alternative to transforming your data when you can’t waive the normality assumption. I also have that table in my Hypothesis Testing book, which you have if I’m remembering correctly.
By the way, if you’re curious about why you can waive the normality assumption, you can thank the central limit theorem . Click the link if you want to see how it works. There’s a very good reason why you can just waive the normality assumption without worrying about it in some cases!
January 18, 2021 at 2:22 pm
Very easy to follow and a nicely structured article ! Thanks for making my life easy!!!
January 19, 2021 at 3:25 pm
You’re very welcome! I’m glad my site has been helpful!
January 17, 2021 at 11:56 pm
When checking for normal distribution property for a given data set, we divide the data in 5 ranges of Z score and then calculate x value and so on.. Is it compulsory to have minimum 5 ranges?
January 19, 2021 at 3:26 pm
Hi Nikee, I’d just us a normality test, such as the Anderson-Darling test . Or use a normal probability plot .
January 4, 2021 at 12:40 am
Hi! Can you please tell me what are the applications of normal distribution?
January 4, 2021 at 4:04 pm
Well this article covers exactly that! Read it and if you questions about the specific applications, don’t hesitate to ask!
December 30, 2020 at 10:27 am
What is normality test & why it conducted, discuss results using soft ware for data from water resources iterms of normality or non normality
December 31, 2020 at 12:45 am
Hi, you use a normality test to determine whether your data diverges from the normal distribution. I write about distribution tests in general, of which a normality test is just one specific type, in my post about identifying the distribution of your data . Included in the discussion and the output I use for the example is a normality test and interpretation. Click that link to read more about it. Additionally, my Hypothesis Testing book covers normality tests in more details.
December 7, 2020 at 6:43 pm
Hi Jim, could you explain how the normal distribution is related to the linear regression?
December 7, 2020 at 11:06 pm
The main way that the normal distribution relates to regression is through the residuals. If you be able to trust the hypothesis testing (p-values, CIs), the residuals should be normally distributed. If they’re not normally distributed, you can’t trust those results. For more information about that, read my post about OLS regression assumptions .
December 7, 2020 at 6:59 am
Have one question which I am finding it difficult to answer. Why is it useful to see if other types of distributions can be approximated to a normal distribution?
Appreciate if you can briefly explain
December 7, 2020 at 11:17 pm
The main reason that comes to my mind is for ease of calculations in hypothesis testing. For example, some tests such proportions tests (which use the binomial distribution) and the Poisson rate tests (for count data and use the Poisson distribution) have a form that uses a normal approximation tests. These normal approximation tests uses Z-scores for the normal distribution rather than values for the “native” distribution.
The main reason these normal approximation tests exist is because they’re easier for students to calculate by hand in statistics classes. Also, I assume in the pre-computer days it was also a plus. However, the normal distribution only approximates these other distributions in certain circumstances and it’s important to know whether your data fit those requirements, otherwise the normal approximation tests will be inaccurate. Additionally, you should use t-tests to compare means when you have an estimate of the population distribution, which is almost always the case. Technically, Z-tests are for cases when you know the population standard deviation (almost never). However, when your sample size is large enough, the t-distribution approximates the normal distribution and you can use a Z-test. Again, that’s easier to calculate by hand.
With computers, I’d recommend using the appropriate distribution for each test rather than the normal approximation.
I show how this works in my Hypothesis Testing book .
There’s another context where normal approximation becomes important. That’s the central limit theorem, which states that as the sample size increases, the sampling distribution of the mean approximates the normal distribution even when the distribution of values is non-normal. For more information about that, read my post about the central limit theorem .
Those are the mains reason I can think of! I hope that helps!
November 22, 2020 at 9:33 pm
What does random variable X̄ (capital x-bar) mean? How would you describe it?
November 22, 2020 at 10:14 pm
X-bar refers to the variable’s mean.
November 18, 2020 at 6:38 am
Very helpful
November 14, 2020 at 4:33 pm
hi how can i compare between binomial, normal and poisson distribution?
October 14, 2020 at 3:15 am
Dear jim Thank you very much for your post. It clarifies many notions. I have an issue I hope you have the answer. To combie forecasting models, I have chosen to calculte the weights based on the normal distribution. This latter is fitted on the past observation of the data I am forecasting. In this case are the weights equal to the PDF or should I treat it as an error measure, so it would be equal to 1/PDF ???
September 25, 2020 at 3:44 am
My problem in interpreting normal and poisson distribution remains. When you want to calculate the probability of selling a random number of apples in a week for instance and you want to work this out with excel spreadsheet How do you know when to subtract your answer from one or not? Is the mean the sole reference?
September 23, 2020 at 11:23 am
Thank you for your your post. I have one small question concerning the Empirical Rule (68%, 95%, 99.7%):
In a normal distribution, 68% of the observations will fall between +/- 1 standard deviation from the mean.
For example, the lateral deviation of a dart from the middle of the bullseye is defined by a normal distribution with a mean of 0 cm and a standard deviation of 5 cm. Would it be possible to affirm that there is a probability of 68% that the dart will hit the board inside a ring of radius of 5 cm?
I’m confused because for me the probability of having a lateral deviation smaller than the standard deviation (x < 1 m ) is 84%.
September 24, 2020 at 11:08 pm
Hi Thibert,
If it was me playing darts, the standard deviation would be much higher than 5 cm!
So, your question is really about two aspects: accuracy and precision.
Accuracy has to do with where the darts fall on average. The mean of zero indicates that on average the darts center on the bullseye. If it had been a non-zero value, the darts would have been centered elsewhere.
The standard deviation has to do with precision, which is how close to the target the darts tend to hit. Because the darts clustered around the bullseye and have a standard deviation of 5cm, you’d be able to say that 68% of darts will fall within 5cm of the bullseye assuming the distances follow a normal distribution (or at least fairly close).
I’m not sure what you’re getting at with the lateral deviation being less than the standard deviation? I thought you were defining it as the standard deviation? I’m also not sure where you’re getting 84% from? It’s possible I’m missing something that you’re asking about.
August 23, 2020 at 6:14 am
I hope this question is relevant. I’ve been trying to find an answer to this question for quite some time. Is it possible to correlate two samples if one is normally distributed and the other is not normally distributed? Many thanks for your time.
August 24, 2020 at 12:22 am
When you’re talking about Pearson’s correlation between two continuous variables, it assumes that the two variables follow a bivariate normal distribution. Defining that is a bit complicated! Read here for a technical definition . However, when you have more than 25 observations, you can often disregard this assumption.
Additionally, as I write in my post about correlation , you should graph the data. Sometimes it graph is an obvious way to know when you won’t get good results!
August 20, 2020 at 11:24 pm
Awesome explanation Jim, all doubts about Z score got cleared up. by any chance do you have a soft copy of your book. or is it available in India? Thanks.
August 21, 2020 at 12:58 am
Hi Archana, I’m glad this post was helpful!
You can get my ebooks from anywhere in the world. Just go to My Store .
My Introduction to Statistics book, which is the one that covers the normal distribution among others, is also available in print. You should be able to order that from your preferred online retailer or ask a local bookstore to order it (ISBN: 9781735431109).
August 14, 2020 at 5:11 am
super explanation
August 12, 2020 at 4:18 am
you can use Python Numpy library random.normal
July 30, 2020 at 12:35 am
Experimentalists always aspire to have data having normal distribution but in real it shifts from the normal distribution behaviour. How his issue is addressed to approximate the values
July 31, 2020 at 5:13 pm
I’m always surprised at how often the normal distribution actually fits real data. And, in regression analysis, is often not hard to get the residuals to follow a normal distribution. However, when the data/residuals absolutely don’t follow the normal distribution, all is not lost! For one thing, the central limit theorem allows you to use many parametric tests even with nonnormal data. You can also use nonparametric tests with nonnormal data. And, while I always consider it a last resort, you can transform the data so it follows the normal distribution.
July 21, 2020 at 3:15 am
Blood pressure of 150 doctors was recorded. The mean BP was found to be 12.7 mmHG. The standard deviation was calculated to be 6mmHG. If blood pressure is normally distributed then how many doctors will have systolic blood pressure above 133 mmHG?
July 21, 2020 at 3:41 am
Calculate the Z-score for the value in question. I’m guessing that is 13.3 mmHG rather than 133! I show how to do that in this article. Then use a Z-table to look up that Z-score, which I also show in this article. You can find online Z-tables to help you out.
July 13, 2020 at 6:03 am
Good day professor
I would like to what is the different between ” sampling on the mean of value” and “normal distribution”. I really appreciate any help from you Thank
July 14, 2020 at 2:06 pm
I’m not really clear about what you’re asking. Normal distribution is a probability function that explains how values of a population/sample are distributed. I’m not sure what you mean by “sampling on the mean of value”? However, if you take a sample, you can calculate the mean for that sample. If you collected a random sample, then the sample mean is an unbiased estimator of the population mean. Further, if the population follows a normal distribution, then the mean also serves as one of the two parameters for the normal distribution, the other being the standard deviation.
July 8, 2020 at 7:25 am
Hello sir! I am a student, and have little knowledge about statistics and probability. How can I answer this (normal curve analysis), given by my teacher, here as follows: A production machine has a normally distributed daily output in units. The average daily output is 4000 and daily output standard deviation is 500. What is the probability that the production of one random day will be below 3580?
Thank you so much and God bless you! 🙂
July 8, 2020 at 3:34 pm
You’re looking at the right article to calculate your answer! The first step is for you to calculate your Z-score. Look for the section titled–Standardization: How to Calculate Z-scores. You need to calculate the Z-score for the value of 3580.
After calculating your z-score, look at the section titled–Using a Table of Z-scores. You won’t be able to use the little snippet of a table that include there, but there are online Z score tables . You need to find the proportion of the area under the curve to left of your z-score. That proportion is your probability! Hint: Because the value you’re considering (3580) is below the mean (4000), you will have a negative Z-score.
If you’d like me to verify your answer, I’d be happy to do that. Just post it here.
June 11, 2020 at 12:50 pm
I would like to cite your book in my journal paper but I can’t find its ISBN. Could you please provide me the ISBN?
April 24, 2020 at 7:56 am
Yours works really helped me to understand about normal distributions. Thank you so much
April 21, 2020 at 12:13 pm
Wow I loved this post, for someone who knows nothing about statistics, it really helped me understand why you would use this in a practical sense. I’m trying to follow a course on Udemy on BI that simply describes Normal Distribution and how it works, but without giving any understanding of why its used and how it could be used with examples. So, having the apples and oranges description really helped me!
April 23, 2020 at 12:58 am
Hi Michael,
Your kind comment totally made my day! Thanks so much!
April 19, 2020 at 12:40 am
I am still a newbie in statistics. I have curious question.
I have always heard people saying they need to make data to be of normal distribution before running prediction models.
And i have heard many methods, one which is standardisation and others are log transformation/cube root etc.
If i have a dataset that has both age and weight variables and the distribution are not normal. Should i use transform them using the Z score standardisation or can i use other methods such as log transformation to normalise them? Or should i log transform them first, and then standardise them again using Z score?
I can’t really wrap my head around these..
Thank you much!
April 20, 2020 at 3:34 am
Usually for predictive models, such as using regression analysis, it’s the residuals that have to be normally distributed rather than the dependent variable itself. If you the residuals are not normal, transforming the dependent variable is one possible solution. However, that should be a last resort. There are other possible solutions you should try first, which I describe in my post about least squares assumptions .
March 24, 2020 at 7:30 am
Sir, Can I have the reference ID of yours to add to my paper
March 11, 2020 at 5:19 am
In case of any skewed data, some transformation like log transformation can be attempted. In most of the cases, the log transformation reduces the skewness. With transformed Mean and SD, find the 95% confidence Interval that is Mean – 2SD to Mean+2SD. Having obtained the transformed confidence interval, take antilog of the lower and upper limit. Now, any value not falling in the confidence interval can be treated as an outlier.
March 2, 2020 at 8:33 am
Hi Jim, Thanks for the wonderful explanation. I have been doing a Target setting exercise and my data is skewed. In this scenario, how to apprpach Target setting? Also, how to approach outlier detection for skewed data. Thanks in advance.
February 14, 2020 at 12:03 am
Why do we need to use z-score when the apple and orange have the same unit measurement (gram) ?
February 20, 2020 at 4:07 pm
Even when you use the same measurement, z-scores can still provide helpful information. In the example, I show how the z-scores for each show where they fall within their own distribution and they also highlight the fact that we’re comparing a very underweight orange to a somewhat overweight apple.
February 13, 2020 at 3:00 am
In the “Example of Using Standard Scores to Make an Apples to Oranges Comparison” section, Could you explain detail the meaning when we have a z-score of apple and orange ?
February 13, 2020 at 11:40 am
I compare those two scores and explain what they mean. I’m not sure what more you need?
January 27, 2020 at 5:59 am
Hi! I have a data report which gives Mean = 1.91, S.D. = 1.06, N=22. The data range is between 1 and 5. Is it possible to generate the 22 points of the data from this information. Thanks.
January 28, 2020 at 11:46 pm
Unfortunately, you can’t reconstruct a dataset using those values.
January 26, 2020 at 9:06 pm
Okay..now I’ve got it. Thank you so much. And your post is really helpful to me. Actually because of this I can complete my notes..thank you..✨
January 26, 2020 at 1:37 am
In different posts about Normal Distribution they have written Varience as a parameter even my teacher also include Varience as the parameter. So it’s really confusing that on what basis the standard deviation is as parameter and on what basis the others say Varience as parameter.
And I’m really sorry for bothering you again and again…🙂
January 26, 2020 at 6:32 pm
I don’t know why they have confused those two terms but they are different. Standard deviation and variances are definitely different but related. Variance is not a parameter for the normal distribution. The square root of the variance is the standard deviation, which is a parameter.
January 25, 2020 at 3:53 am
Hi! It’s really helpful.. thank you so much. But I have a confusion that the one of the parameter of normal Distribution is Standard deviation. Is we can also say that the parameter of standard deviation is “Varience” .
January 26, 2020 at 12:10 am
Standard deviations and variances are two different measures of variation. They are related but different. The standard deviation is the square root of the variance. Read my post about measures of variability and focus on the sections about those measures for more information.
January 17, 2020 at 6:34 am
This is a great explanation for why we standardize values and the significance of a z-score. You managed to explain a concept that multiple professors and online trainings were unable to explain.
Though I was able to understand the formulae and how to calculate all these values, I was unable to understand WHY we needed to do it. Your post made that very clear to me!
Thank you for taking the time to put this together and for picking examples that make so much sense!
January 8, 2020 at 11:27 am
Hi Jim, thanks for an awesome blog. Currently I am busy with an assignment for university where I got a broad task, I have to find out if a specific independent variable and a specific dependent variable are linearly related in a hedonic pricing model.
In plain English, would checking for the linear relationship mean that I check the significance level of the specific independent variable within the broader hedonic pricing model? If so, should I check for anything else? If I am completely wrong, what would you advise me to do instead?
Sorry for such a long question, but me and classmates are a bit lost over the ambiguity of the assignment, as we are all not that familiar with statistics.
I thank you for your time!
January 10, 2020 at 10:05 am
Measures of statistical significance won’t indicate the nature of the relationship between two variables. For example, if you have a curved, positive relationship between X and Y, you might still obtain a significant result if you fit a straight line relationship between the two. To really see the nature of the relationship between variables, you should graph them in a scatterplot.
I hope this helps!
January 7, 2020 at 5:58 am
your blog is awesome I’v confusion … When we add or subtract 0.5 area?
January 7, 2020 at 10:48 am
Hi Ibrahim,
Sorry, but I don’t understand what you’re asking. Can you provide more details?
December 23, 2019 at 1:36 am
Hello Jim! How did (30+-2)*5 = 140-160 become 20 to 40 minutes?
Looking forward to your reply.. Thanks!
December 23, 2019 at 3:19 am
Hi Anupama,
You have to remember your order of operations in math! You put your parentheses in the wrong place. What I wrote is equivalent to 30 +/- (2*5). Remember, multiplication before addition and subtraction. 🙂
December 1, 2019 at 11:23 pm
what are the three different ways to find probabilities for normal distribution?
December 2, 2019 at 9:30 am
Hi Mark, if I understand your question correctly, you’ll find your answers in this blog post.
November 15, 2019 at 7:40 am
for really you have opened my eyes
November 15, 2019 at 1:35 am
Hi jim,why is normal distribution important. how can you access normality using graphical techniques like histogram and box plot
November 15, 2019 at 11:23 pm
I’d recommend using a normal probability plot to graphically assess normality. I write about it in this post that compares histograms and normal probability plots .
October 23, 2019 at 10:57 am
Check your Pearson’s coefficient of skew. 26 “high outliers” sounds to me like you have right-tailed aka positive skew, possibly. Potentially, it is only moderately skewed so you can still assume normality. If it is highly skewed, you need to transform it and then do calculations. Transforming is way easier than it sounds; Google can show you how to do that.
October 23, 2019 at 11:39 am
Hi Cynthia,
This is a case where diagnosing the situation can be difficult without the actual dataset. For others, here’s the original comment in question .
On the one hand, having 26 high outliers and only 3 low outliers does give the impression of a skew. However, we can’t tell the extremeness of the high versus low outliers. Perhaps the high outliers are less extreme?
On the other hand, the commenter wrote that a normality test indicated the distribution is normally distributed and that a histogram also looks normally distributed. Furthermore, the fact that the mean and median are close together suggests it is a symmetric distribution rather than skewed.
There are a number of uncertainties as well. I don’t know the criteria the original commenter is using to identify outliers. And, I was hoping to determine the sample size. If it’s very large, then even 26 outliers is just a small fraction and might be within the bounds of randomness.
On the whole, the bulk of the evidence suggests that the data follow a normal distribution. It’s hard to say for sure. But, it sounds like we can rule out a severe skew at the very least.
You mention using a data transformation. And, you’re correct, they’re fairly easy to use. However, I’m not a big fan of transforming data. I consider it a last resort and not my “go to” option. The problem is that you’re analyzing the transformed data rather than the original data. Consequently, the results are not intuitive. Fortunately, thanks the central limit theorem , you often don’t need to transform the data even when they are skewed. That’s not to say that I’d never transform data, I’d just look for other options first.
You also mention checking the Pearson’s coefficient of skewness, which is a great idea. However, for this specific case, it’s probably pretty low. You calculate this coefficient by finding the difference between the mean and median, multiplying that by three, and then dividing by the standard deviation. For this case, the commenter indicated the the mean and median were very close together, which means the numerator in this calculation is small and, hence, the coefficient of skewness is small. But, you’re right, it’s a good statistic to look at in general.
Thanks for writing and adding your thoughts to the discussion!
October 20, 2019 at 9:03 am
Thank you very much Jim,I understand this better
September 16, 2019 at 3:22 pm
What if my distribution has a like 26 outliers on the high end and 3 on the low end and still my mean and median happen to be pretty close. the distribution on a histogram looks normal too. and the ryan joiner test produces the p-value of >1.00. will this distribution be normal?
September 16, 2019 at 3:31 pm
Based on what you write, it sure sounds like it’s normally distributed. What’s your sample size and how are you defining outliers?
August 21, 2019 at 4:44 pm
i just want to say thanks a lot Jim, greetings from mexico
August 21, 2019 at 4:46 pm
You’re very welcome!!! 🙂
August 1, 2019 at 4:34 am
Thank you very much Jim. You have simplified this for me and I found it very easy to understand everything.
July 3, 2019 at 1:50 am
Your blog is wonderful. Thanks a lot.
May 17, 2019 at 9:28 am
Dear JIm, I want to compare trends of R&D expenditures before and after crisis, and i was planning to use paired t test or its non parametric alternative. But, before of that, i employed normality tests, and i have had one problem. But, normality test shows that one variable has normal, and other has non normal distribution. So, my question is should i use T paired test or it non parametric alternative. You can see results in the table. Thank you. Kolm.Smirn Stat(p) SHapiro-Wilk Stat(p) Before crisis 0.131(0.200) 0.994(0.992) After crisis 0.431(0.003) 0.697(0.009)
May 17, 2019 at 10:26 am
There are several other issues in addition to normality that you should consider. And, nonnormally distributed data doesn’t necessarily indicate you can’t use a parametric test, such as a paired t-test. I detail the various things you need to factor into your decision in this blog post: Parametric vs. Nonparametric tests . That post should answer your questions!
May 17, 2019 at 5:11 am
I’m trying to refresh Stats & Probability after being away from it for about 10 years. Your blog is really helping me out.
May 14, 2019 at 6:04 pm
Very useful post. I will be visiting your blog again!
May 4, 2019 at 3:11 am
Great. The simple yet practical explanation helped me a lot
April 24, 2019 at 4:08 am
You made an error with the calculation for the apples and oranges: You said 110-100/15 = 0.667 but that is wrong because 110-100/15=110-6.667=103.333
April 24, 2019 at 10:50 am
Thanks for catching that! Actually, the answer is correct (0.667), but I should have put parentheses in the correct places. I’ll add those. Although, I did define how to calculate Z-scores with an equation in the previous section.
For that example, a score of 110 in a population that has a mean of 100 and a standard deviation of 15 has a Z-score of 0.667. It is two-thirds of a standard deviation above the mean. If it truly had a Z-score of 103.333, it would be 103 standard deviations above the mean which is remarkably far out in the tail of the distribution!
April 8, 2019 at 9:05 pm
Thank you Jim
Is there a tutorial that you know of that explains how to do this please
April 8, 2019 at 11:17 am
How did you produce your apa style graphs I need to show where my score lies on a normal distribution
Did you use Spss to produce the graphs shown here please
April 8, 2019 at 11:23 am
I used Minitab statistical software to create the graphs.
March 28, 2019 at 3:47 am
Material is very informative. Taken the extract of this for my lecture. Udaya Simha
March 27, 2019 at 10:22 am
I was hoping that you could help me with my z scores for my assignment. Specifically I need help with interpreting the data!!!!
I need to compare my my z scores for each of the big five personality traits to that of my peers in the unit
The population mean for Openness was 85.9 with standard deviation of 11.8. My score was 71. Which gives me a z score of -1.26
The population mean for Agreeableness was 91.5, standard deviation was 11. My score was 94. Which gives me a z score of 0.23
Now the part I am having trouble with is I need to work out how much higher, lower or approximately average I am on each trait domain compared to my peers and I literally have no idea how I go about this!
I understand that a score of 0.23 is in the range of one SD above the mean but it is only slightly above the mean which would make my agreeableness score approximately average to my peers, is this correct ? and is there a more statistical way of determining how far above or below the mean say in % way or via percentile rank
please help
P.S I think your site is wonderful and I am now able to graph my assignment appropriately because of you! your site is fantastic
March 17, 2019 at 7:01 am
Pretty much good..😊
February 24, 2019 at 6:52 pm
Hi Jim, This is great. I’ve got a class of kids with chrome books and I’m trying to teach with tools we have. Namely Google sheets. Excel uses many of the same Stats functions. I don’t like to have them use any function unless I can really explain what it does. I want to know the math behind it. But some of the math is beyond what they would have. Still I like them to have a visual idea of what’s happening. I think we rely too much on calculator/ spreadsheet functions without really understanding what they do and how they work. Most of the time the functions are straight forward. But this one was weird. I ran through 8 Stats books and I really didn’t get a good feeling of how it worked. I can approximate a normal distribution curve of a dataset using norm.dist(), but I wanted to know more about why it worked. First we will look at a few generic datasets. Then they will pull in stock data and they will tell me if current stock prices fall within 1 standard deviation of a years worth of data. Fun. Thanks!! Elizabeth
February 24, 2019 at 7:08 pm
Hi Elizabeth,
That sounds fantastic that you’re teaching them these tools! And, I entirely agree that we often rely to much on functions and numbers without graphing what we’re doing.
For this particular function, a graph would make it very clear. I do explain probability functions in the post that I link you to in my previous comment, and I use graphs for both discrete and continuous distributions. Unfortunately, I don’t show a cumulative probability function (I should really add that!). For the example I describe, imagine the bell curve of a normal distribution, the value of 42 is above the mean, and you shade the curve for all values less than equal to 42. You’re shading about 90.87% of the distribution for the cumulative probability.
That does sound like fun! 🙂
February 23, 2019 at 8:28 pm
This is really neat. I’ve been looking at the formula norm.dist(x, Mean, StandardDev, False) in Excel and Google Sheets. I’m trying to understand what it is actually calculating. I’m just getting back into Statistics – and this one is stumping me. This is where x is a point in the dataset
February 24, 2019 at 6:33 pm
I don’t use Excel for statistics, but I did take a look into this function.
Basically, you’re defining the parameters of a normal distribution (mean and standard deviation) and supply an X-value that you’re interested in. You can use this Excel function to derive the cumulative probability for your X-value or the probability of that specific value. Here’s an example that Microsoft uses on its Help page for the norm.dist function .
If you have a normal distribution that has a mean of 40, standard deviation of 1.5, and you’re interested in the properties of the value 42 for this distribution. This function indicates that the cumulative probability for this value is 0.90. In other words, the probability that values in this distribution will be less than or equal to 42 is 90.87%. Said in another way, values of 42 and less comprise about 90.87% of this distribution.
Alternatively, this Excel function can calculate the probability of an observation having the value of 42 exactly. There’s a caveat because this distribution is for a continuous variable and it is unlikely that an observation will have a value of exactly 42 out to a infinite number of decimal places. So, these calculations use a small range of values that includes 42 and calculates the probability that a value falls within that small range. That’s known as the probability distribution function (PDF). In this case, the probability of a value being 42 equals approximately 10.9%.
For more information about PDFs, please read my post about Understanding Probability Distributions .
January 27, 2019 at 1:51 am
Hey Jim. This is a fantastic post. I came across a lot of people asking the significance of normal distribution (more people should) and I was looking for an answer that puts its as eloquently as you did. Thank you for writing this.
January 27, 2019 at 10:55 pm
Hi, thank you so much! I really appreciate your kind words! 🙂
January 21, 2019 at 11:55 pm
Excellent Jim, great explanation. I have a doubt, you used some software to calculate Z-score and to display graphs right, can you please let me know which software you used for the same?
January 22, 2019 at 12:43 am
Hi Sudhakar,
I’m using Minitab statistical software.
Thanks for reading!
January 5, 2019 at 5:30 am
Great to have met someone like Jim who can explain Statistics in plain language for everyone to understand. Another questions are; a) what is the function of probability distribution and would one use a probability distribution?
January 7, 2019 at 12:11 am
I’ve written a post all about probability distributions. I include the link to it in this post, but here it is again: Understanding Probability Distributions .
December 18, 2018 at 8:11 am
Very nice explanation .
November 18, 2018 at 5:40 am
Finally I found a post which explains normal distribution in plain english. It helped me a lot to understand the basic concepts. Thank you very much, Jim
November 19, 2018 at 10:04 am
You’re very welcome, Xavier! It’s great to hear that it was helpful!
November 15, 2018 at 7:42 pm
Hi Jim thanks for this. How large a number makes normal distribution?
November 16, 2018 at 3:26 pm
Hi, I don’t understand your question. A sample of any size can follow a normal distribution. However, when your sample is very small, it’s hard to determine which distribution it follows. Additionally, there is no sample size that guarantees your data follows a normal distribution. For example, you can have a very large sample size that follows a skewed, non-normal distribution.
Are you possibly thinking about the central limit theorem? This theorem states that the sampling distribution of the mean follows a normal distribution if your sample size is sufficiently large. If this is what you’re asking about, read my post on the central limit theorem for more information.
October 22, 2018 at 11:37 am
best post ever, thanks a lot
October 22, 2018 at 11:41 am
Thanks, Ranjan!
October 14, 2018 at 10:46 pm
Great work So many confusion cleared
October 12, 2018 at 9:43 am
thank you very much for this very good explanation of normal distribution 👍🙌🏻
October 12, 2018 at 1:58 pm
October 10, 2018 at 8:50 am
During my B.E (8 semester course), we had “Engg. Maths.” for four semesters, and in the one semester we had Prob & Stat. (along with other topics), which was purely theoretical even though we had lots of exercises and problems, could not digest and didnt knew its practical significane, (i.e., how and where to apply and use) and again in MTech (3 sem course) we had one subject “Reliability Analysis and Design of Structures” , but this was relatively more practically oriented. While working in Ready Mix Concrete industry and while doing PhD in concrete, I came across this Normal Distribution concept, where concrete mix design is purely based on Std Dev and Z score, and also concrete test results are assesed statistically for their performance monitoring, acceptace criteria, non-compliance etc., where normal distribution is the back-bone. However because of my thirst to gain knowledge, to fully understand, a habit of browsing internet (I wanted Confidence Interval concept) made me to meet your website accidentally.
I observed your effort in explaining the topic in a simple, meaningful and understandable manner, even for a person with non-science or Engg background can learn from scratch with zero-background. That’s great.
My heart felt gratitude and regards and appreciate you for your volunteering mentality (broad mind) in sharing your knowledge from your experience to the needy global society. Thank you once again, Rajendra Prabhu
September 25, 2018 at 6:25 am
THANK YOU FOR YOUR HELP
VERY USEFUL
September 21, 2018 at 1:15 pm
thank you, very useful
September 18, 2018 at 1:16 pm
Jim, you truly love what you are doing, and saving us at the same time. i just want to say thank you i was about to give up on statistics because of formulas with no words
September 18, 2018 at 3:50 pm
Hi Ali, Thank you so much! I really appreciate your kind words! Yes, I absolutely love statistics. I also love helping other learn and appreciate statistics as well. I don’t always agree with the usual way statistics is taught, so I wanted to provide an alternative!
September 16, 2018 at 5:34 pm
I was frustrated in my statistics learning by the lecturer’s focus on formulae. While obviously critical, they were done in isolation so I could not see the underlying rationale and where they fit in. Your posts make that very clear, and explain the context, the connections and limitations while also working through the calculations. Thank you.
September 18, 2018 at 12:19 am
First, I’m so happy to hear that my post have been helpful! What you describe are exactly my goals for my website. So, your kind words mean so much to me! Thank you!
July 12, 2018 at 2:49 pm
Nice work sir…
July 9, 2018 at 2:24 am
Fantastic way of explaining
July 9, 2018 at 2:44 am
Thank you, Sanjay!
July 5, 2018 at 5:57 pm
Sir kindly guide me. I have panel data. My all variables are not normally distributed. data is in ratios form. My question is that , For descriptive statistics and correlation analysis, do i need to use raw data in its original form?? and transformed data for regression analysis only?
Moreover, which transformation method should be used for ratios, when data is highly positively or negatively skewed. I tried, log, difference, reciprocal, but could not get the normality.
Kindly help me. Thank You
July 5, 2018 at 1:25 pm
Do natural phenomena such as hemoglobin levels or the weight of ants really follow a normal distribution? If you add up a large number of random events, you get a normal distribution.
July 5, 2018 at 2:48 pm
To obtain a normal distribution, you need the random errors to have an equal probability of being positive and negative and the errors are more likely to be small than large.
Many datasets will naturally follow the normal distribution. For example, the height data in this blog post are real data and they follow the normal distribution. However, not all datasets and variables have that tendency. The weight data for the same subjects that I used for the weight data are not normally distributed. Those data are right skewed–which you can read about in my post about identifying the distribution of a dataset.
May 24, 2018 at 6:29 pm
Hello Jim, first of all, your page is very good, it has helped me a lot to understand statistics. Query, then when I have a data set that is not distributed normally, should I first transform them to normal and then start working them? Greetings from Chile, CLT
May 25, 2018 at 2:27 pm
This gets a little tricky. For one thing, it depends what you want do with the data. If you’re talking about hypothesis tests, you can often use the regular tests with non-normal data when you have a sufficiently large sample size. “Sufficiently large” isn’t really even that large. You can also use nonparametric tests for nonnormal data. There are several issues to consider, which I write about in my post that compares parametric and nonparametric hypothesis tests .
That should help clarify some of the issues. After reading that, let me now if you have any additional questions. Generally, I’m not a fan of transforming data because it completely changes the properties of your data.
May 7, 2018 at 11:43 am
Hi Jim. What exactly do you mean by a true normal distribution. You’ve not used the word “true” anywhere in your post. Just plain normal distribution.
May 7, 2018 at 4:59 pm
Hi Aashay, sorry about the confusing terminology. What I meant by true normal distribution is one that follows a normal distribution to mathematically perfect degree. For example, the graphs of all the normal distributions in this post are true normal distributions because the statistical software graphs them based on the equation for the normal distribution plus the parameter values for the inputs.
By the way, there is not one shape that corresponds to a true normal distribution. Instead, there are an infinite number and they’re all based on the infinite number of different means and standard deviations that you can input into the equation for the normal distribution.
Typically, data don’t follow the normal distribution exactly. A distribution test can determine whether the deviation from the normal distribution is statistically significant.
In the comment where I used this terminology, I was just trying to indicate how as a distribution deviated from a true normal distribution, the Empirical Rule also deviates.
I hope this helps.
May 1, 2018 at 6:30 am
I’m glad I stumbled across your blog 🙂 Wonderful work!! I’ve gained an new perspective on what statistics could mean to me
May 1, 2018 at 11:00 pm
Hi Josh, that is awesome! My goal is to show that statistics can actually be exciting! So, your comment means a lot to me! Thanks!
April 30, 2018 at 11:59 pm
Excellent…..
May 1, 2018 at 12:01 am
Thank you, Asis!
April 30, 2018 at 10:48 pm
Many Many thanks for help dear Jim sir!
May 1, 2018 at 12:02 am
You’re very welcome! 🙂
April 30, 2018 at 1:15 pm
dear Jim, tell me please what is normality?. and how we can understand to use normal or any other distribution for a data set?
April 30, 2018 at 2:15 pm
Hi Muhammad, you’re in the right place to find the information that you need! This blog post tells you all about the normal distribution. Normality simply refers to data that are normally distributed (i.e., the data follow the normal distribution).
I have links in this post to another post called Understand Probability Distributions that tells you about other distributions. And yet another link to a post that tells you How to Determine the Distribution of Your Data.
April 30, 2018 at 4:16 am
your are far better than my teachers. Thank you Jim
April 30, 2018 at 9:51 am
Thank you, Masum!
April 30, 2018 at 12:34 am
Another great post. Simple, clear and direct language and logic.
April 30, 2018 at 9:55 am
Thanks so much! That’s always my goal–so your kind words mean a lot to me!
April 30, 2018 at 12:21 am
I was eagerly waitng fr ths topic .. Normal distribution Thnks a lott ,,,,,,
April 30, 2018 at 12:26 am
You’re very welcome, Khursheed!
April 29, 2018 at 11:20 pm
Jim, it is my understanding that the normal distribution is unique and it is the one that follows to perfection the 68 95 99.7%. The rest of the distributions are “approximately” normal, as you say when they get wider. They are still symmetric but not normal because they lost perfection to the empirical rule. I was taught this by a professor when I was doing my master;s in Stats
April 30, 2018 at 12:17 am
Hi Fernando, all normal distributions (for those cases where you input any values for the mean and standard deviation parameters) follow the Empirical Rule (68%, 95%, 99.7%). There are other symmetric distributions that aren’t quite normal distributions. I think you’re referring to these symmetric distributions that have thicker or thinner tails than normal distributions should. Kurtosis measures the thickness of the tails. Distributions with high kurtosis have thicker tails and those with low kurtosis has thinner tails. If a distribution has thicker or thinner tails than the true normal distribution, then the Empirical Rule doesn’t hold true. How off the rule is depends on how different the distribution is from a true normal distribution. Some of these distributions can be considered approximately normal.
However, this gets confusing because you can have true normal distributions that have wider spreads than other normal distributions. This spread doesn’t necessarily make them non-normal. The example of the wider distribution that I show in the Standard Deviation section is a true normal distribution. These wider normal distributions follow the Empirical Rule. If you have sample data and are trying to determine whether they follow a normal distribution, perform a normality test.
On the other hand, there are other distributions that are not symmetrical at all and very different from the normal distribution. They’re different by more than just the thickness of the tails. For example the lognormal distribution can model very skewed distributions. Some of these distributions are nowhere close to being approximately normal!
So, you can have a wide variety of non-normal distributions that range from approximately normal to not close at all!
April 29, 2018 at 10:41 pm
Thank you very much for your great post. Cheers from MA
April 29, 2018 at 10:46 pm
You’re very welcome! I’m glad it was helpful! 🙂
Comments and Questions Cancel reply
Normality test
One of the most common assumptions for statistical tests is that the data used are normally distributed. For example, if you want to run a t-test or an ANOVA , you must first test whether the data or variables are normally distributed.
The assumption of normal distribution is also important for linear regression analysis , but in this case it is important that the error made by the model is normally distributed, not the data itself.
Nonparametric tests
If the data are not normally distributed, the above procedures cannot be used and non-parametric tests must be used. Non-parametric tests do not assume that the data are normally distributed.
How is the normal distribution tested?
Normal distribution can be tested either analytically (statistical tests) or graphically. The most common analytical tests to check data for normal distribution are the:
- Kolmogorov-Smirnov Test
- Shapiro-Wilk Test
- Anderson-Darling Test
For graphical verification, either a histogram or, better, the Q-Q plot is used. Q-Q stands for quantile-quantile plot, where the actually observed distribution is compared with the theoretically expected distribution.
Statistical tests for normal distribution
To test your data analytically for normal distribution, there are several test procedures, the best known being the Kolmogorov-Smirnov test, the Shapiro-Wilk test, and the Anderson Darling test.

In all of these tests, you are testing the null hypothesis that your data are normally distributed. The null hypothesis is that the frequency distribution of your data is normally distributed. To reject or not reject the null hypothesis, all these tests give you a p-value . What matters is whether this p-value is less than or greater than 0.05.

If the p-value is less than 0.05, this is interpreted as a significant deviation from the normal distribution and it can be assumed that the data are not normally distributed. If the p-value is greater than 0.05 and you want to be statistically clean, you cannot necessarily say that the frequency distribution is normal, you just cannot reject the null hypothesis.
In practice, a normal distribution is assumed for values greater than 0.05, although this is not entirely correct. Nevertheless, the graphical solution should always be considered.
Note: The Kolmogorov-Smirnov test and the Anderson-Darling test can also be used to test distributions other than the normal distribution.
Disadvantage of the analytical tests for normal distribution
Unfortunately, the analytical method has a major drawback, which is why more and more attention is being paid to graphical methods.
The problem is that the calculated p-value is affected by the size of the sample. Therefore, if you have a very small sample, your p-value may be much larger than 0.05, but if you have a very very large sample from the same population, your p-value may be smaller than 0.05.
If we assume that the distribution in the population deviates only slightly from the normal distribution, we will get a very large p-value with a very small sample and therefore assume that the data are normally distributed. However, if you take a larger sample, the p-value gets smaller and smaller, even though the samples are from the same population with the same distribution. With a very large sample, you can even get a p-value of less than 0.05, rejecting the null hypothesis of normal distribution.
To avoid this problem, graphical methods are increasingly being used.
Graphical test for normal distribution
If the normal distribution is tested graphically, one looks either at the histogram or even better the QQ plot.
If you want to check the normal distribution using a histogram, plot the normal distribution on the histogram of your data and check that the distribution curve of the data approximately matches the normal distribution curve.
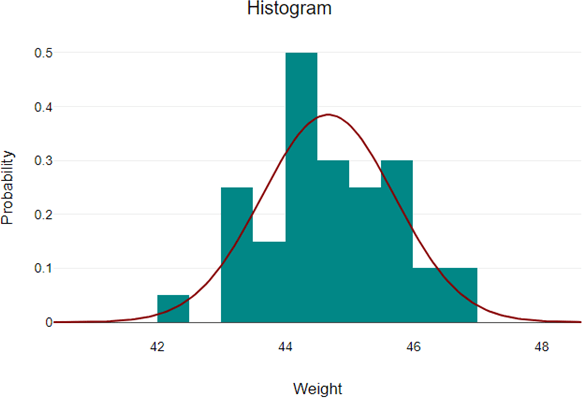
A better way to do this is to use a quantile-quantile plot, or Q-Q plot for short. This compares the theoretical quantiles that the data should have if they were perfectly normal with the quantiles of the measured values.
If the data were perfectly normally distributed, all points would lie on the line. The further the data deviates from the line, the less normally distributed the data is.
In addition, DATAtab plots the 95% confidence interval. If all or almost all of the data fall within this interval, this is a very strong indication that the data are normally distributed. They are not normally distributed if, for example, they form an arc and are far from the line in some areas.

Test Normal distribution in DATAtab
When you test your data for normal distribution with DATAtab, you get the following evaluation, first the analytical test procedures clearly arranged in a table, then the graphical test procedures.
If you want to test your data for normal distribution, simply copy your data into the table on DATAtab, click on descriptive statistics and then select the variable you want to test for normal distribution. Then, just click on Test Normal Distribution and you will get the results.
Furthermore, if you are calculating a hypothesis test with DATAtab, you can test the assumptions for each hypothesis test, if one of the assumptions is the normal distribution, then you will get the test for normal distribution in the same way.
Statistics made easy
- many illustrative examples
- ideal for exams and theses
- statistics made easy on 412 pages
- 5rd revised edition (April 2024)
- Only 8.99 €

"Super simple written"
"It could not be simpler"
"So many helpful examples"

Cite DATAtab: DATAtab Team (2024). DATAtab: Online Statistics Calculator. DATAtab e.U. Graz, Austria. URL https://datatab.net
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Hypothesis Testing | A Step-by-Step Guide with Easy Examples
Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.
There are 5 main steps in hypothesis testing:
- State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a or H 1 ).
- Collect data in a way designed to test the hypothesis.
- Perform an appropriate statistical test .
- Decide whether to reject or fail to reject your null hypothesis.
- Present the findings in your results and discussion section.
Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.
Table of contents
Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.
After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.
The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.
- H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.
There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).
If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.
Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.
Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .
- an estimate of the difference in average height between the two groups.
- a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.
Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.
In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.
In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).
The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .
In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.
In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.
However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.
If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”
These are superficial differences; you can see that they mean the same thing.
You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.
If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.
A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved August 21, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/
Is this article helpful?
Rebecca Bevans
Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.
9.3 Distribution Needed for Hypothesis Testing
Earlier in the course, we discussed sampling distributions. Particular distributions are associated with hypothesis testing. Perform tests of a population mean using a normal distribution or a Student's t -distribution . (Remember, use a Student's t -distribution when the population standard deviation is unknown and the distribution of the sample mean is approximately normal.) We perform tests of a population proportion using a normal distribution (usually n is large).
Assumptions
When you perform a hypothesis test of a single population mean μ using a Student's t -distribution (often called a t -test), there are fundamental assumptions that need to be met in order for the test to work properly. Your data should be a simple random sample that comes from a population that is approximately normally distributed . You use the sample standard deviation to approximate the population standard deviation. Note that if the sample size is sufficiently large, a t -test will work even if the population is not approximately normally distributed.
When you perform a hypothesis test of a single population mean μ using a normal distribution (often called a z -test), you take a simple random sample from the population. The population you are testing is normally distributed or your sample size is sufficiently large. You know the value of the population standard deviation which, in reality, is rarely known.
When you perform a hypothesis test of a single population proportion p , you take a simple random sample from the population. You must meet the conditions for a binomial distribution , which are the following: there are a certain number n of independent trials, the outcomes of any trial are success or failure, and each trial has the same probability of a success p . The shape of the binomial distribution needs to be similar to the shape of the normal distribution. To ensure this, the quantities np and nq must both be greater than five ( np > 5 and nq > 5). Then the binomial distribution of a sample (estimated) proportion can be approximated by the normal distribution with μ = p and σ = p q n σ = p q n . Remember that q = 1 – p .
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.
Access for free at https://openstax.org/books/statistics/pages/1-introduction
- Authors: Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Statistics
- Publication date: Mar 27, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/statistics/pages/1-introduction
- Section URL: https://openstax.org/books/statistics/pages/9-3-distribution-needed-for-hypothesis-testing
© Apr 16, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Numbers & Quantities

Statistics & Probability

More Learning Tools
Encyclopedia
Pen & Paper exercises
Excel / GeoGebra recipes
Tutor-on-Demand
Junior Math
Multiplication Master
Treasure Trail
Wind Surfer
Stack n´load
Language: English
How to Do Hypothesis Testing with Normal Distribution
Hypothesis tests compare a result against something you already believe is true. Let X 1 , X 2 , … , X n be n independent random variables with equal expected value μ and standard deviation σ . Let X be the mean of these n random variables, so
The stochastic variable X has an expected value μ and a standard deviation σ n . You want to perform a hypothesis test on this expected value. You have a null hypothesis H 0 : μ = μ 0 and three possible alternative hypotheses: H a : μ < μ 0 , H a : μ > μ 0 or H a : μ ≠ μ 0 . The first two alternative hypotheses belong to what you call a one-sided test, while the latter is two-sided.
In hypothesis testing, you calculate using the alternative hypothesis in order to say something about the null hypothesis.
Hypothesis Testing (Normal Distribution)
Note! For two-sided testing, multiply the p -value by 2 before checking against the critical region.
As the production manager at the new soft drink factory, you are worried that the machines don’t fill the bottles to their proper capacity. Each bottle should be filled with 0 . 5 L soda, but random samples show that 48 soda bottles have an average of 0 . 4 8 L , with an empirical standard deviation of 0 . 1 . You are wondering if you need to recalibrate the machines so that they become more precise.
This is a classic case of hypothesis testing by normal distribution. You now follow the instructions above and select 1 0 % level of significance, since it is only a quantity of soda and not a case of life and death.
The alternative hypothesis in this case is that the bottles do not contain 0 . 5 L and that the machines are not precise enough. This thus becomes a two-sided hypothesis test and you must therefore remember to multiply the p -value by 2 before deciding whether the p -value is in the critical region. This is because the normal distribution is symmetric, so P ( X ≥ k ) = P ( X ≤ − k ) . Thus it is just as likely to observe an equally extremely high value as an equally extreme low:
so H 0 must be kept, and the machines are deemed to be fine as is.
Had the p -value been less than the level of significance, that would have meant that the calibration represented by the alternative hypothesis would be significantly better for the business.

User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
7.2.2 - hypothesis testing, derivation of the test section .
We are now going to develop the hypothesis test for the difference of two proportions for independent samples. The hypothesis test will follow the same six steps we learned in the previous Lesson although they are not explicitly stated.
We will use the sampling distribution of \(\hat{p}_1-\hat{p}_2\) as we did for the confidence interval. One major difference in the hypothesis test is the null hypothesis and assuming the null hypothesis is true.
For a test for two proportions, we are interested in the difference. If the difference is zero, then they are not different (i.e., they are equal). Therefore, the null hypothesis will always be:
\(H_0\colon p_1-p_2=0\)
Another way to look at it is \(H_0\colon p_1=p_2\). This is worth stopping to think about. Remember, in hypothesis testing, we assume the null hypothesis is true. In this case, it means that \(p_1\) and \(p_2\) are equal. Under this assumption, then \(\hat{p}_1\) and \(\hat{p}_2\) are both estimating the same proportion. Think of this proportion as \(p^*\). Therefore, the sampling distribution of both proportions, \(\hat{p}_1\) and \(\hat{p}_2\), will, under certain conditions, be approximately normal centered around \(p^*\), with standard error \(\sqrt{\dfrac{p^*(1-p^*)}{n_i}}\), for \(i=1, 2\).
We take this into account by finding an estimate for this \(p^*\) using the two sample proportions. We can calculate an estimate of \(p^*\) using the following formula:
\(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}\)
This value is the total number in the desired categories \((x_1+x_2)\) from both samples over the total number of sampling units in the combined sample \((n_1+n_2)\).
Putting everything together, if we assume \(p_1=p_2\), then the sampling distribution of \(\hat{p}_1-\hat{p}_2\) will be approximately normal with mean 0 and standard error of \(\sqrt{p^*(1-p^*)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}\), under certain conditions.
\(z^*=\dfrac{(\hat{p}_1-\hat{p}_2)-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right)}}\)
...will follow a standard normal distribution.
Finally, we can develop our hypothesis test for \(p_1-p_2\).
Null: \(H_0\colon p_1-p_2=0\)
Possible Alternatives:
\(H_a\colon p_1-p_2\ne0\)
\(H_a\colon p_1-p_2>0\)
\(H_a\colon p_1-p_2<0\)
Conditions:
\(n_1\hat{p}_1\), \(n_1(1-\hat{p}_1)\), \(n_2\hat{p}_2\), and \(n_2(1-\hat{p}_2)\) are all greater than five
The test statistic is:
\(z^*=\dfrac{\hat{p}_1-\hat{p}_2-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\dfrac{1}{n_1}+\dfrac{1}{n_2}\right)}}\)
...where \(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}\).
The critical values, rejection regions, p-values, and decisions will all follow the same steps as those from a hypothesis test for a one sample proportion.
Example 7-2: Received $100 by Mistake Section

Let's continue with the question that was asked previously.
Males and females were asked about what they would do if they received a $100 bill by mail, addressed to their neighbor, but wrongly delivered to them. Would they return it to their neighbor? Of the 69 males sampled, 52 said “yes” and of the 131 females sampled, 120 said “yes.”
Does the data indicate that the proportions that said “yes” are different for males and females at a 5% level of significance? Conduct the test using the p-value approach.
- Using Minitab
Again, let’s define males as sample 1.
The conditions are all satisfied as we have shown previously.
The null and alternative hypotheses are:
\(H_0\colon p_1-p_2=0\) vs \(H_a\colon p_1-p_2\ne 0\)
The test statistic:
\(n_1=69\), \(\hat{p}_1=\frac{52}{69}\)
\(n_2=131\), \(\hat{p}_2=\frac{120}{131}\)
\(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}=\dfrac{52+120}{69+131}=\dfrac{172}{200}=0.86\)
\(z^*=\dfrac{\hat{p}_1-\hat{p}_2-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}=\dfrac{\dfrac{52}{69}-\dfrac{120}{131}}{\sqrt{0.86(1-0.86)\left(\frac{1}{69}+\frac{1}{131}\right)}}=-3.1466\)
The p-value of the test based on the two-sided alternative is:
\(\text{p-value}=2P(Z>|-3.1466|)=2P(Z>3.1466)=2(0.0008)=0.0016\)
Since our p-value of 0.0016 is less than our significance level of 5%, we reject the null hypothesis. There is enough evidence to suggest that proportions of males and females who would return the money are different.
Minitab: Inference for Two Proportions with Independent Samples
To conduct inference for two proportions with an independent sample in Minitab...
The following window will appear. In the drop-down choose ‘Summarized data’ and entered the number of events and trials for both samples.
You should get the following output for this example:
Test and CI for Two Proportions
| Sample | X | N | Sample p |
|---|---|---|---|
| 1 | 52 | 69 | 0.753623 |
| 2 | 120 | 131 | 0.916031 |
Difference = p (1) - p (2)
Estimate for difference: -0.162407
95% CI for difference: (-0.274625, -0.0501900)
Test for difference = 0 (vs ≠ 0): Z = -3.15 P-Value = 0.002 (Use this!)
Fisher's exact test: P-Value = 0.003 (Ignore the Fisher's exact test. This test uses a different method to calculate a test statistic from the Z-test we have learned in this lesson.)
Ignore the Fisher's p -value! The p -value highlighted above is calculated using the methods we learned in this lesson. The Fisher's test uses a different method than what we explained in this lesson to calculate a test statistic and p -value. This method incorporates a log of the ratio of observed to expected values. It's just a different technique that is more complicated to do by-hand. Minitab automatically includes both results in its output.
Try it! Section
In 1980, of 750 men 20-34 years old, 130 were found to be overweight. Whereas, in 1990, of 700 men, 20-34 years old, 160 were found to be overweight.
At the 5% significance level, do the data provide sufficient evidence to conclude that, for men 20-34 years old, a higher percentage were overweight in 1990 than 10 years earlier? Conduct the test using the p-value approach.
Let’s define 1990 as sample 1.
\(H_0\colon p_1-p_2=0\) vs \(H_a\colon p_1-p_2>0\)
\(n_1=700\), \(\hat{p}_1=\frac{160}{700}\)
\(n_2=750\), \(\hat{p}_2=\frac{130}{750}\)
\(\hat{p}^*=\dfrac{x_1+x_2}{n_1+n_2}=\dfrac{160+130}{700+750}=\dfrac{290}{1450}=0.2\)
The conditions are all satisfied: \(n_1\hat{p}_1\), \(n_1(1-\hat{p}_1)\), \(n_2\hat{p}_2\), and \(n_2(1-\hat{p}_2)\) are all greater than 5.
\(z^*=\dfrac{\hat{p}_1-\hat{p}_2-0}{\sqrt{\hat{p}^*(1-\hat{p}^*)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}=\dfrac{\dfrac{160}{700}-\dfrac{130}{750}}{\sqrt{0.2(1-0.2)\left(\frac{1}{700}+\frac{1}{750}\right)}}=2.6277\)
The p-value of the test based on the right-tailed alternative is:
\(\text{p-value}=P(Z>2.6277)=0.0043\)
Since our p-value of 0.0043 is less than our significance level of 5%, we reject the null hypothesis. There is enough evidence to suggest that the proportion of males overweight in 1990 is greater than the proportion in 1980.
Using Minitab
To conduct inference for two proportions with independent samples in Minitab...
- Choose Stat > Basic Statistics > 2 proportions
- Choose Options
Select "Difference < hypothesized difference" for 'Alternative Hypothesis.
You should get the following output.
| Sample | X | N | Sample p |
|---|---|---|---|
| 1 | 130 | 750 | 0.173333 |
| 2 | 160 | 700 | 0.228571 |
Estimate for difference: -0.0552381
95% upper bound for difference: -0.0206200
Test for difference = 0 (vs < 0): Z = -2.63 P-Value = 0.004
Fisher's exact test: P-Value = 0.005 (Ignore the Fisher's exact test)
An Introduction to Bayesian Thinking
Chapter 5 hypothesis testing with normal populations.
In Section 3.5 , we described how the Bayes factors can be used for hypothesis testing. Now we will use the Bayes factors to compare normal means, i.e., test whether the mean of a population is zero or compare the means of two groups of normally-distributed populations. We divide this mission into three cases: known variance for a single population, unknown variance for a single population using paired data, and unknown variance using two independent groups.
Also note that some of the examples in this section use an updated version of the bayes_inference function. If your local output is different from what is seen in this chapter, or the provided code fails to run for you please make sure that you have the most recent version of the package.
5.1 Bayes Factors for Testing a Normal Mean: variance known
Now we show how to obtain Bayes factors for testing hypothesis about a normal mean, where the variance is known . To start, let’s consider a random sample of observations from a normal population with mean \(\mu\) and pre-specified variance \(\sigma^2\) . We consider testing whether the population mean \(\mu\) is equal to \(m_0\) or not.
Therefore, we can formulate the data and hypotheses as below:
Data \[Y_1, \cdots, Y_n \mathrel{\mathop{\sim}\limits^{\rm iid}}\textsf{Normal}(\mu, \sigma^2)\]
- \(H_1: \mu = m_0\)
- \(H_2: \mu \neq m_0\)
We also need to specify priors for \(\mu\) under both hypotheses. Under \(H_1\) , we assume that \(\mu\) is exactly \(m_0\) , so this occurs with probability 1 under \(H_1\) . Now under \(H_2\) , \(\mu\) is unspecified, so we describe our prior uncertainty with the conjugate normal distribution centered at \(m_0\) and with a variance \(\sigma^2/\mathbf{n_0}\) . This is centered at the hypothesized value \(m_0\) , and it seems that the mean is equally likely to be larger or smaller than \(m_0\) , so a dividing factor \(n_0\) is given to the variance. The hyper parameter \(n_0\) controls the precision of the prior as before.
In mathematical terms, the priors are:
- \(H_1: \mu = m_0 \text{ with probability 1}\)
- \(H_2: \mu \sim \textsf{Normal}(m_0, \sigma^2/\mathbf{n_0})\)
Bayes Factor
Now the Bayes factor for comparing \(H_1\) to \(H_2\) is the ratio of the distribution, the data under the assumption that \(\mu = m_0\) to the distribution of the data under \(H_2\) .
\[\begin{aligned} \textit{BF}[H_1 : H_2] &= \frac{p(\text{data}\mid \mu = m_0, \sigma^2 )} {\int p(\text{data}\mid \mu, \sigma^2) p(\mu \mid m_0, \mathbf{n_0}, \sigma^2)\, d \mu} \\ \textit{BF}[H_1 : H_2] &=\left(\frac{n + \mathbf{n_0}}{\mathbf{n_0}} \right)^{1/2} \exp\left\{-\frac 1 2 \frac{n }{n + \mathbf{n_0}} Z^2 \right\} \\ Z &= \frac{(\bar{Y} - m_0)}{\sigma/\sqrt{n}} \end{aligned}\]
The term in the denominator requires integration to account for the uncertainty in \(\mu\) under \(H_2\) . And it can be shown that the Bayes factor is a function of the observed sampled size, the prior sample size \(n_0\) and a \(Z\) score.
Let’s explore how the hyperparameters in \(n_0\) influences the Bayes factor in Equation (5.1) . For illustration we will use the sample size of 100. Recall that for estimation, we interpreted \(n_0\) as a prior sample size and considered the limiting case where \(n_0\) goes to zero as a non-informative or reference prior.
\[\begin{equation} \textsf{BF}[H_1 : H_2] = \left(\frac{n + \mathbf{n_0}}{\mathbf{n_0}}\right)^{1/2} \exp\left\{-\frac{1}{2} \frac{n }{n + \mathbf{n_0}} Z^2 \right\} \tag{5.1} \end{equation}\]
Figure 5.1 shows the Bayes factor for comparing \(H_1\) to \(H_2\) on the y-axis as \(n_0\) changes on the x-axis. The different lines correspond to different values of the \(Z\) score or how many standard errors \(\bar{y}\) is from the hypothesized mean. As expected, larger values of the \(Z\) score favor \(H_2\) .

Figure 5.1: Vague prior for mu: n=100
But as \(n_0\) becomes smaller and approaches 0, the first term in the Bayes factor goes to infinity, while the exponential term involving the data goes to a constant and is ignored. In the limit as \(n_0 \rightarrow 0\) under this noninformative prior, the Bayes factor paradoxically ends up favoring \(H_1\) regardless of the value of \(\bar{y}\) .
The takeaway from this is that we cannot use improper priors with \(n_0 = 0\) , if we are going to test our hypothesis that \(\mu = n_0\) . Similarly, vague priors that use a small value of \(n_0\) are not recommended due to the sensitivity of the results to the choice of an arbitrarily small value of \(n_0\) .
This problem arises with vague priors – the Bayes factor favors the null model \(H_1\) even when the data are far away from the value under the null – are known as the Bartlett’s paradox or the Jeffrey’s-Lindleys paradox.
Now, one way to understand the effect of prior is through the standard effect size
\[\delta = \frac{\mu - m_0}{\sigma}.\] The prior of the standard effect size is
\[\delta \mid H_2 \sim \textsf{Normal}(0, \frac{1}{\mathbf{n_0}})\]
This allows us to think about a standardized effect independent of the units of the problem. One default choice is using the unit information prior, where the prior sample size \(n_0\) is 1, leading to a standard normal for the standardized effect size. This is depicted with the blue normal density in Figure 5.2 . This suggested that we expect that the mean will be within \(\pm 1.96\) standard deviations of the hypothesized mean with probability 0.95 . (Note that we can say this only under a Bayesian setting.)
In many fields we expect that the effect will be small relative to \(\sigma\) . If we do not expect to see large effects, then we may want to use a more informative prior on the effect size as the density in orange with \(n_0 = 4\) . So they expected the mean to be within \(\pm 1/\sqrt{n_0}\) or five standard deviations of the prior mean.

Figure 5.2: Prior on standard effect size
Example 1.1 To illustrate, we give an example from parapsychological research. The case involved the test of the subject’s claim to affect a series of randomly generated 0’s and 1’s by means of extra sensory perception (ESP). The random sequence of 0’s and 1’s are generated by a machine with probability of generating 1 being 0.5. The subject claims that his ESP would make the sample mean differ significantly from 0.5.
Therefore, we are testing \(H_1: \mu = 0.5\) versus \(H_2: \mu \neq 0.5\) . Let’s use a prior that suggests we do not expect a large effect which leads the following solution for \(n_0\) . Assume we want a standard effect of 0.03, there is a 95% chance that it is between \((-0.03/\sigma, 0.03/\sigma)\) , with \(n_0 = (1.96\sigma/0.03)^2 = 32.7^2\) .
Figure 5.3 shows our informative prior in blue, while the unit information prior is in orange. On this scale, the unit information prior needs to be almost uniform for the range that we are interested.

Figure 5.3: Prior effect in the extra sensory perception test
A very large data set with over 104 million trials was collected to test this hypothesis, so we use a normal distribution to approximate the distribution the sample mean.
- Sample size: \(n = 1.0449 \times 10^8\)
- Sample mean: \(\bar{y} = 0.500177\) , standard deviation \(\sigma = 0.5\)
- \(Z\) -score: 3.61
Now using our prior in the data, the Bayes factor for \(H_1\) to \(H_2\) was 0.46, implying evidence against the hypothesis \(H_1\) that \(\mu = 0.5\) .
- Informative \(\textit{BF}[H_1:H_2] = 0.46\)
- \(\textit{BF}[H_2:H_1] = 1/\textit{BF}[H_1:H_2] = 2.19\)
Now, this can be inverted to provide the evidence in favor of \(H_2\) . The evidence suggests that the hypothesis that the machine operates with a probability that is not 0.5, is 2.19 times more likely than the hypothesis the probability is 0.5. Based on the interpretation of Bayes factors from Table 3.5 , this is in the range of “not worth the bare mention”.
To recap, we present expressions for calculating Bayes factors for a normal model with a specified variance. We show that the improper reference priors for \(\mu\) when \(n_0 = 0\) , or vague priors where \(n_0\) is arbitrarily small, lead to Bayes factors that favor the null hypothesis regardless of the data, and thus should not be used for hypothesis testing.
Bayes factors with normal priors can be sensitive to the choice of the \(n_0\) . While the default value of \(n_0 = 1\) is reasonable in many cases, this may be too non-informative if one expects more effects. Wherever possible, think about how large an effect you expect and use that information to help select the \(n_0\) .
All the ESP examples suggest weak evidence and favored the machine generating random 0’s and 1’s with a probability that is different from 0.5. Note that ESP is not the only explanation – a deviation from 0.5 can also occur if the random number generator is biased. Bias in the stream of random numbers in our pseudorandom numbers has huge implications for numerous fields that depend on simulation. If the context had been about detecting a small bias in random numbers what prior would you use and how would it change the outcome? You can experiment it in R or other software packages that generate random Bernoulli trials.
Next, we will look at Bayes factors in normal models with unknown variances using the Cauchy prior so that results are less sensitive to the choice of \(n_0\) .
5.2 Comparing Two Paired Means using Bayes Factors
We previously learned that we can use a paired t-test to compare means from two paired samples. In this section, we will show how Bayes factors can be expressed as a function of the t-statistic for comparing the means and provide posterior probabilities of the hypothesis that whether the means are equal or different.
Example 5.1 Trace metals in drinking water affect the flavor, and unusually high concentrations can pose a health hazard. Ten pairs of data were taken measuring the zinc concentration in bottom and surface water at ten randomly sampled locations, as listed in Table 5.1 .
Water samples collected at the the same location, on the surface and the bottom, cannot be assumed to be independent of each other. However, it may be reasonable to assume that the differences in the concentration at the bottom and the surface in randomly sampled locations are independent of each other.
| location | bottom | surface | difference |
|---|---|---|---|
| 1 | 0.430 | 0.415 | 0.015 |
| 2 | 0.266 | 0.238 | 0.028 |
| 3 | 0.567 | 0.390 | 0.177 |
| 4 | 0.531 | 0.410 | 0.121 |
| 5 | 0.707 | 0.605 | 0.102 |
| 6 | 0.716 | 0.609 | 0.107 |
| 7 | 0.651 | 0.632 | 0.019 |
| 8 | 0.589 | 0.523 | 0.066 |
| 9 | 0.469 | 0.411 | 0.058 |
| 10 | 0.723 | 0.612 | 0.111 |
To start modeling, we will treat the ten differences as a random sample from a normal population where the parameter of interest is the difference between the average zinc concentration at the bottom and the average zinc concentration at the surface, or the main difference, \(\mu\) .
In mathematical terms, we have
- Random sample of \(n= 10\) differences \(Y_1, \ldots, Y_n\)
- Normal population with mean \(\mu \equiv \mu_B - \mu_S\)
In this case, we have no information about the variability in the data, and we will treat the variance, \(\sigma^2\) , as unknown.
The hypothesis of the main concentration at the surface and bottom are the same is equivalent to saying \(\mu = 0\) . The second hypothesis is that the difference between the mean bottom and surface concentrations, or equivalently that the mean difference \(\mu \neq 0\) .
In other words, we are going to compare the following hypotheses:
- \(H_1: \mu_B = \mu_S \Leftrightarrow \mu = 0\)
- \(H_2: \mu_B \neq \mu_S \Leftrightarrow \mu \neq 0\)
The Bayes factor is the ratio between the distributions of the data under each hypothesis, which does not depend on any unknown parameters.
\[\textit{BF}[H_1 : H_2] = \frac{p(\text{data}\mid H_1)} {p(\text{data}\mid H_2)}\]
To obtain the Bayes factor, we need to use integration over the prior distributions under each hypothesis to obtain those distributions of the data.
\[\textit{BF}[H_1 : H_2] = \iint p(\text{data}\mid \mu, \sigma^2) p(\mu \mid \sigma^2) p(\sigma^2 \mid H_2)\, d \mu \, d\sigma^2\]
This requires specifying the following priors:
- \(\mu \mid \sigma^2, H_2 \sim \textsf{Normal}(0, \sigma^2/n_0)\)
- \(p(\sigma^2) \propto 1/\sigma^2\) for both \(H_1\) and \(H_2\)
\(\mu\) is exactly zero under the hypothesis \(H_1\) . For \(\mu\) in \(H_2\) , we start with the same conjugate normal prior as we used in Section 5.1 – testing the normal mean with known variance. Since we assume that \(\sigma^2\) is known, we model \(\mu \mid \sigma^2\) instead of \(\mu\) itself.
The \(\sigma^2\) appears in both the numerator and denominator of the Bayes factor. For default or reference case, we use the Jeffreys prior (a.k.a. reference prior) on \(\sigma^2\) . As long as we have more than two observations, this (improper) prior will lead to a proper posterior.
After integration and rearranging, one can derive a simple expression for the Bayes factor:
\[\textit{BF}[H_1 : H_2] = \left(\frac{n + n_0}{n_0} \right)^{1/2} \left( \frac{ t^2 \frac{n_0}{n + n_0} + \nu } { t^2 + \nu} \right)^{\frac{\nu + 1}{2}}\]
This is a function of the t-statistic
\[t = \frac{|\bar{Y}|}{s/\sqrt{n}},\]
where \(s\) is the sample standard deviation and the degrees of freedom \(\nu = n-1\) (sample size minus one).
As we saw in the case of Bayes factors with known variance, we cannot use the improper prior on \(\mu\) because when \(n_0 \to 0\) , then \(\textit{BF}[H1:H_2] \to \infty\) favoring \(H_1\) regardless of the magnitude of the t-statistic. Arbitrary, vague small choices for \(n_0\) also lead to arbitrary large Bayes factors in favor of \(H_1\) . Another example of the Barlett’s or Jeffreys-Lindley paradox.
Sir Herald Jeffrey discovered another paradox testing using the conjugant normal prior, known as the information paradox . His thought experiment assumed that our sample size \(n\) and the prior sample size \(n_0\) . He then considered what would happen to the Bayes factor as the sample mean moved further and further away from the hypothesized mean, measured in terms standard errors with the t-statistic, i.e., \(|t| \to \infty\) . As the t-statistic or information about the mean moved further and further from zero, the Bayes factor goes to a constant depending on \(n, n_0\) rather than providing overwhelming support for \(H_2\) .
The bounded Bayes factor is
\[\textit{BF}[H_1 : H_2] \to \left( \frac{n_0}{n_0 + n} \right)^{\frac{n - 1}{2}}\]
Jeffrey wanted a prior with \(\textit{BF}[H_1 : H_2] \to 0\) (or equivalently, \(\textit{BF}[H_2 : H_1] \to \infty\) ), as the information from the t-statistic grows, indicating the sample mean is as far as from the hypothesized mean and should favor \(H_2\) .
To resolve the paradox when the information the t-statistic favors \(H_2\) but the Bayes factor does not, Jeffreys showed that no normal prior could resolve the paradox .
But a Cauchy prior on \(\mu\) , would resolve it. In this way, \(\textit{BF}[H_2 : H_1]\) goes to infinity as the sample mean becomes further away from the hypothesized mean. Recall that the Cauchy prior is written as \(\textsf{C}(0, r^2 \sigma^2)\) . While Jeffreys used a default of \(r = 1\) , smaller values of \(r\) can be used if smaller effects are expected.
The combination of the Jeffrey’s prior on \(\sigma^2\) and this Cauchy prior on \(\mu\) under \(H_2\) is sometimes referred to as the Jeffrey-Zellener-Siow prior .
However, there is no closed form expressions for the Bayes factor under the Cauchy distribution. To obtain the Bayes factor, we must use the numerical integration or simulation methods.
We will use the function from the package to test whether the mean difference is zero in Example 5.1 (zinc), using the JZS (Jeffreys-Zellener-Siow) prior.

With equal prior probabilities on the two hypothesis, the Bayes factor is the posterior odds. From the output, we see this indicates that the hypothesis \(H_2\) , the mean difference is different from 0, is almost 51 times more likely than the hypothesis \(H_1\) that the average concentration is the same at the surface and the bottom.
To sum up, we have used the Cauchy prior as a default prior testing hypothesis about a normal mean when variances are unknown. This does require numerical integration, but it is available in the function from the package. If you expect that the effect sizes will be small, smaller values of \(r\) are recommended.
It is often important to quantify the magnitude of the difference in addition to testing. The Cauchy Prior provides a default prior for both testing and inference; it avoids problems that arise with choosing a value of \(n_0\) (prior sample size) in both cases. In the next section, we will illustrate using the Cauchy prior for comparing two means from independent normal samples.
5.3 Comparing Independent Means: Hypothesis Testing
In the previous section, we described Bayes factors for testing whether the mean difference of paired samples was zero. In this section, we will consider a slightly different problem – we have two independent samples, and we would like to test the hypothesis that the means are different or equal.
Example 5.2 We illustrate the testing of independent groups with data from a 2004 survey of birth records from North Carolina, which are available in the package.
The variable of interest is – the weight gain of mothers during pregnancy. We have two groups defined by the categorical variable, , with levels, younger mom and older mom.
Question of interest : Do the data provide convincing evidence of a difference between the average weight gain of older moms and the average weight gain of younger moms?
We will view the data as a random sample from two populations, older and younger moms. The two groups are modeled as:
\[\begin{equation} \begin{aligned} Y_{O,i} & \mathrel{\mathop{\sim}\limits^{\rm iid}} \textsf{N}(\mu + \alpha/2, \sigma^2) \\ Y_{Y,i} & \mathrel{\mathop{\sim}\limits^{\rm iid}} \textsf{N}(\mu - \alpha/2, \sigma^2) \end{aligned} \tag{5.2} \end{equation}\]
The model for weight gain for older moms using the subscript \(O\) , and it assumes that the observations are independent and identically distributed, with a mean \(\mu+\alpha/2\) and variance \(\sigma^2\) .
For the younger women, the observations with the subscript \(Y\) are independent and identically distributed with a mean \(\mu-\alpha/2\) and variance \(\sigma^2\) .
Using this representation of the means in the two groups, the difference in means simplifies to \(\alpha\) – the parameter of interest.
\[(\mu + \alpha/2) - (\mu - \alpha/2) = \alpha\]
You may ask, “Why don’t we set the average weight gain of older women to \(\mu+\alpha\) , and the average weight gain of younger women to \(\mu\) ?” We need the parameter \(\alpha\) to be present in both \(Y_{O,i}\) (the group of older women) and \(Y_{Y,i}\) (the group of younger women).
We have the following competing hypotheses:
- \(H_1: \alpha = 0 \Leftrightarrow\) The means are not different.
- \(H_2: \alpha \neq 0 \Leftrightarrow\) The means are different.
In this representation, \(\mu\) represents the overall weight gain for all women. (Does the model in Equation (5.2) make more sense now?) To test the hypothesis, we need to specify prior distributions for \(\alpha\) under \(H_2\) (c.f. \(\alpha = 0\) under \(H_1\) ) and priors for \(\mu,\sigma^2\) under both hypotheses.
Recall that the Bayes factor is the ratio of the distribution of the data under the two hypotheses.
\[\begin{aligned} \textit{BF}[H_1 : H_2] &= \frac{p(\text{data}\mid H_1)} {p(\text{data}\mid H_2)} \\ &= \frac{\iint p(\text{data}\mid \alpha = 0,\mu, \sigma^2 )p(\mu, \sigma^2 \mid H_1) \, d\mu \,d\sigma^2} {\int \iint p(\text{data}\mid \alpha, \mu, \sigma^2) p(\alpha \mid \sigma^2) p(\mu, \sigma^2 \mid H_2) \, d \mu \, d\sigma^2 \, d \alpha} \end{aligned}\]
As before, we need to average over uncertainty and the parameters to obtain the unconditional distribution of the data. Now, as in the test about a single mean, we cannot use improper or non-informative priors for \(\alpha\) for testing.
Under \(H_2\) , we use the Cauchy prior for \(\alpha\) , or equivalently, the Cauchy prior on the standardized effect \(\delta\) with the scale of \(r\) :
\[\delta = \alpha/\sigma^2 \sim \textsf{C}(0, r^2)\]
Now, under both \(H_1\) and \(H_2\) , we use the Jeffrey’s reference prior on \(\mu\) and \(\sigma^2\) :
\[p(\mu, \sigma^2) \propto 1/\sigma^2\]
While this is an improper prior on \(\mu\) , this does not suffer from the Bartlett’s-Lindley’s-Jeffreys’ paradox as \(\mu\) is a common parameter in the model in \(H_1\) and \(H_2\) . This is another example of the Jeffreys-Zellner-Siow prior.
As in the single mean case, we will need numerical algorithms to obtain the Bayes factor. Now the following output illustrates testing of Bayes factors, using the Bayes inference function from the package.

We see that the Bayes factor for \(H_1\) to \(H_2\) is about 5.7, with positive support for \(H_1\) that there is no difference in average weight gain between younger and older women. Using equal prior probabilities, the probability that there is a difference in average weight gain between the two groups is about 0.15 given the data. Based on the interpretation of Bayes factors from Table 3.5 , this is in the range of “positive” (between 3 and 20).
To recap, we have illustrated testing hypotheses about population means with two independent samples, using a Cauchy prior on the difference in the means. One assumption that we have made is that the variances are equal in both groups . The case where the variances are unequal is referred to as the Behren-Fisher problem, and this is beyond the scope for this course. In the next section, we will look at another example to put everything together with testing and discuss summarizing results.
5.4 Inference after Testing
In this section, we will work through another example for comparing two means using both hypothesis tests and interval estimates, with an informative prior. We will also illustrate how to adjust the credible interval after testing.
Example 5.3 We will use the North Carolina survey data to examine the relationship between infant birth weight and whether the mother smoked during pregnancy. The response variable, , is the birth weight of the baby in pounds. The categorical variable provides the status of the mother as a smoker or non-smoker.
We would like to answer two questions:
Is there a difference in average birth weight between the two groups?
If there is a difference, how large is the effect?
As before, we need to specify models for the data and priors. We treat the data as a random sample for the two populations, smokers and non-smokers.
The birth weights of babies born to non-smokers, designated by a subgroup \(N\) , are assumed to be independent and identically distributed from a normal distribution with mean \(\mu + \alpha/2\) , as in Section 5.3 .
\[Y_{N,i} \mathrel{\mathop{\sim}\limits^{\rm iid}}\textsf{Normal}(\mu + \alpha/2, \sigma^2)\]
While the birth weights of the babies born to smokers, designated by the subgroup \(S\) , are also assumed to have a normal distribution, but with mean \(\mu - \alpha/2\) .
\[Y_{S,i} \mathrel{\mathop{\sim}\limits^{\rm iid}}\textsf{Normal}(\mu - \alpha/2, \sigma^2)\]
The difference in the average birth weights is the parameter \(\alpha\) , because
\[(\mu + \alpha/2) - (\mu - \alpha/2) = \alpha\] .
The hypotheses that we will test are \(H_1: \alpha = 0\) versus \(H_2: \alpha \ne 0\) .
We will still use the Jeffreys-Zellner-Siow Cauchy prior. However, since we may expect the standardized effect size to not be as strong, we will use a scale of \(r = 0.5\) rather than 1.
Therefore, under \(H_2\) , we have \[\delta = \alpha/\sigma \sim \textsf{C}(0, r^2), \text{ with } r = 0.5.\]
Under both \(H_1\) and \(H_2\) , we will use the reference priors on \(\mu\) and \(\sigma^2\) :
\[\begin{aligned} p(\mu) &\propto 1 \\ p(\sigma^2) &\propto 1/\sigma^2 \end{aligned}\]
The input to the base inference function is similar, but now we will specify that \(r = 0.5\) .

We see that the Bayes factor is 1.44, which weakly favors there being a difference in average birth weights for babies whose mothers are smokers versus mothers who did not smoke. Converting this to a probability, we find that there is about a 60% chance of the average birth weights are different.
While looking at evidence of there being a difference is useful, Bayes factors and posterior probabilities do not convey any information about the magnitude of the effect. Reporting a credible interval or the complete posterior distribution is more relevant for quantifying the magnitude of the effect.
Using the function, we can generate samples from the posterior distribution under \(H_2\) using the option.
The 2.5 and 97.5 percentiles for the difference in the means provide a 95% credible interval of 0.023 to 0.57 pounds for the difference in average birth weight. The MCMC output shows not only summaries about the difference in the mean \(\alpha\) , but the other parameters in the model.
In particular, the Cauchy prior arises by placing a gamma prior on \(n_0\) and the conjugate normal prior. This provides quantiles about \(n_0\) after updating with the current data.
The row labeled effect size is the standardized effect size \(\delta\) , indicating that the effects are indeed small relative to the noise in the data.

Figure 5.4: Estimates of effect under H2
Figure 5.4 shows the posterior density for the difference in means, with the 95% credible interval indicated by the shaded area. Under \(H_2\) , there is a 95% chance that the average birth weight of babies born to non-smokers is 0.023 to 0.57 pounds higher than that of babies born to smokers.
The previous statement assumes that \(H_2\) is true and is a conditional probability statement. In mathematical terms, the statement is equivalent to
\[P(0.023 < \alpha < 0.57 \mid \text{data}, H_2) = 0.95\]
However, we still have quite a bit of uncertainty based on the current data, because given the data, the probability of \(H_2\) being true is 0.59.
\[P(H_2 \mid \text{data}) = 0.59\]
Using the law of total probability, we can compute the probability that \(\mu\) is between 0.023 and 0.57 as below:
\[\begin{aligned} & P(0.023 < \alpha < 0.57 \mid \text{data}) \\ = & P(0.023 < \alpha < 0.57 \mid \text{data}, H_1)P(H_1 \mid \text{data}) + P(0.023 < \alpha < 0.57 \mid \text{data}, H_2)P(H_2 \mid \text{data}) \\ = & I( 0 \text{ in CI }) P(H_1 \mid \text{data}) + 0.95 \times P(H_2 \mid \text{data}) \\ = & 0 \times 0.41 + 0.95 \times 0.59 = 0.5605 \end{aligned}\]
Finally, we get that the probability that \(\alpha\) is in the interval, given the data, averaging over both hypotheses, is roughly 0.56. The unconditional statement is the average birth weight of babies born to nonsmokers is 0.023 to 0.57 pounds higher than that of babies born to smokers with probability 0.56. This adjustment addresses the posterior uncertainty and how likely \(H_2\) is.
To recap, we have illustrated testing, followed by reporting credible intervals, and using a Cauchy prior distribution that assumed smaller standardized effects. After testing, it is common to report credible intervals conditional on \(H_2\) . We also have shown how to adjust the probability of the interval to reflect our posterior uncertainty about \(H_2\) . In the next chapter, we will turn to regression models to incorporate continuous explanatory variables.
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- Int J Endocrinol Metab
- v.10(2); Spring 2012

Normality Tests for Statistical Analysis: A Guide for Non-Statisticians
Asghar ghasemi.
1 Endocrine Research Center, Research Institute for Endocrine Sciences, Shahid Beheshti University of Medical Sciences, Tehran, IR Iran
Saleh Zahediasl
Statistical errors are common in scientific literature and about 50% of the published articles have at least one error. The assumption of normality needs to be checked for many statistical procedures, namely parametric tests, because their validity depends on it. The aim of this commentary is to overview checking for normality in statistical analysis using SPSS.
1. Background
Statistical errors are common in scientific literature, and about 50% of the published articles have at least one error ( 1 ). Many of the statistical procedures including correlation, regression, t tests, and analysis of variance, namely parametric tests, are based on the assumption that the data follows a normal distribution or a Gaussian distribution (after Johann Karl Gauss, 1777–1855); that is, it is assumed that the populations from which the samples are taken are normally distributed ( 2 - 5 ). The assumption of normality is especially critical when constructing reference intervals for variables ( 6 ). Normality and other assumptions should be taken seriously, for when these assumptions do not hold, it is impossible to draw accurate and reliable conclusions about reality ( 2 , 7 ).
With large enough sample sizes (> 30 or 40), the violation of the normality assumption should not cause major problems ( 4 ); this implies that we can use parametric procedures even when the data are not normally distributed ( 8 ). If we have samples consisting of hundreds of observations, we can ignore the distribution of the data ( 3 ). According to the central limit theorem, (a) if the sample data are approximately normal then the sampling distribution too will be normal; (b) in large samples (> 30 or 40), the sampling distribution tends to be normal, regardless of the shape of the data ( 2 , 8 ); and (c) means of random samples from any distribution will themselves have normal distribution ( 3 ). Although true normality is considered to be a myth ( 8 ), we can look for normality visually by using normal plots ( 2 , 3 ) or by significance tests, that is, comparing the sample distribution to a normal one ( 2 , 3 ). It is important to ascertain whether data show a serious deviation from normality ( 8 ). The purpose of this report is to overview the procedures for checking normality in statistical analysis using SPSS.
2. Visual Methods
Visual inspection of the distribution may be used for assessing normality, although this approach is usually unreliable and does not guarantee that the distribution is normal ( 2 , 3 , 7 ). However, when data are presented visually, readers of an article can judge the distribution assumption by themselves ( 9 ). The frequency distribution (histogram), stem-and-leaf plot, boxplot, P-P plot (probability-probability plot), and Q-Q plot (quantile-quantile plot) are used for checking normality visually ( 2 ). The frequency distribution that plots the observed values against their frequency, provides both a visual judgment about whether the distribution is bell shaped and insights about gaps in the data and outliers outlying values ( 10 ). The stem-and-leaf plot is a method similar to the histogram, although it retains information about the actual data values ( 8 ). The P-P plot plots the cumulative probability of a variable against the cumulative probability of a particular distribution (e.g., normal distribution). After data are ranked and sorted, the corresponding z-score is calculated for each rank as follows: z = x - ᵪ̅ / s . This is the expected value that the score should have in a normal distribution. The scores are then themselves converted to z-scores. The actual z-scores are plotted against the expected z-scores. If the data are normally distributed, the result would be a straight diagonal line ( 2 ). A Q-Q plot is very similar to the P-P plot except that it plots the quantiles (values that split a data set into equal portions) of the data set instead of every individual score in the data. Moreover, the Q-Q plots are easier to interpret in case of large sample sizes ( 2 ). The boxplot shows the median as a horizontal line inside the box and the interquartile range (range between the 25 th to 75 th percentiles) as the length of the box. The whiskers (line extending from the top and bottom of the box) represent the minimum and maximum values when they are within 1.5 times the interquartile range from either end of the box ( 10 ). Scores greater than 1.5 times the interquartile range are out of the boxplot and are considered as outliers, and those greater than 3 times the interquartile range are extreme outliers. A boxplot that is symmetric with the median line at approximately the center of the box and with symmetric whiskers that are slightly longer than the subsections of the center box suggests that the data may have come from a normal distribution ( 8 ).
3. Normality Tests
The normality tests are supplementary to the graphical assessment of normality ( 8 ). The main tests for the assessment of normality are Kolmogorov-Smirnov (K-S) test ( 7 ), Lilliefors corrected K-S test ( 7 , 10 ), Shapiro-Wilk test ( 7 , 10 ), Anderson-Darling test ( 7 ), Cramer-von Mises test ( 7 ), D’Agostino skewness test ( 7 ), Anscombe-Glynn kurtosis test ( 7 ), D’Agostino-Pearson omnibus test ( 7 ), and the Jarque-Bera test ( 7 ). Among these, K-S is a much used test ( 11 ) and the K-S and Shapiro-Wilk tests can be conducted in the SPSS Explore procedure (Analyze → Descriptive Statistics → Explore → Plots → Normality plots with tests) ( 8 ).
The tests mentioned above compare the scores in the sample to a normally distributed set of scores with the same mean and standard deviation; the null hypothesis is that “sample distribution is normal.” If the test is significant, the distribution is non-normal. For small sample sizes, normality tests have little power to reject the null hypothesis and therefore small samples most often pass normality tests ( 7 ). For large sample sizes, significant results would be derived even in the case of a small deviation from normality ( 2 , 7 ), although this small deviation will not affect the results of a parametric test ( 7 ). The K-S test is an empirical distribution function (EDF) in which the theoretical cumulative distribution function of the test distribution is contrasted with the EDF of the data ( 7 ). A limitation of the K-S test is its high sensitivity to extreme values; the Lilliefors correction renders this test less conservative ( 10 ). It has been reported that the K-S test has low power and it should not be seriously considered for testing normality ( 11 ). Moreover, it is not recommended when parameters are estimated from the data, regardless of sample size ( 12 ).
The Shapiro-Wilk test is based on the correlation between the data and the corresponding normal scores ( 10 ) and provides better power than the K-S test even after the Lilliefors correction ( 12 ). Power is the most frequent measure of the value of a test for normality—the ability to detect whether a sample comes from a non-normal distribution ( 11 ). Some researchers recommend the Shapiro-Wilk test as the best choice for testing the normality of data ( 11 ).
4. Testing Normality Using SPSS
We consider two examples from previously published data: serum magnesium levels in 12–16 year old girls (with normal distribution, n = 30) ( 13 ) and serum thyroid stimulating hormone (TSH) levels in adult control subjects (with non-normal distribution, n = 24) ( 14 ). SPSS provides the K-S (with Lilliefors correction) and the Shapiro-Wilk normality tests and recommends these tests only for a sample size of less than 50 ( 8 ).
In Figure , both frequency distributions and P-P plots show that serum magnesium data follow a normal distribution while serum TSH levels do not. Results of K-S with Lilliefors correction and Shapiro-Wilk normality tests for serum magnesium and TSH levels are shown in Table . It is clear that for serum magnesium concentrations, both tests have a p-value greater than 0.05, which indicates normal distribution of data, while for serum TSH concentrations, data are not normally distributed as both p values are less than 0.05. Lack of symmetry (skewness) and pointiness (kurtosis) are two main ways in which a distribution can deviate from normal. The values for these parameters should be zero in a normal distribution. These values can be converted to a z-score as follows:

| No. | Mean ± SD | Mean ± SEM | Skewness | SE | Z | Kurtosis | SE | Z | K-S With Lilliefors Correction Test | Shapiro-Wilk Test | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Statistics | Df | value | Statistics | Df | -value | |||||||||||
| Serum magnesium, mg/dL | 30 | 2.08 ± 0.175 | 2.08 ± 0.03 | 0.745 | 0.427 | 1.74 | 0.567 | 0.833 | 0.681 | 0.137 | 30 | 0.156 | 0.955 | 30 | 0.236 | |
| Serum TSH , mU/L | 24 | 1.67 ± 1.53 | 1.67 ± 0.31 | 1.594 | 0.472 | 3.38 | 1.401 | 0.918 | 1.52 | 0.230 | 24 | 0.002 | 0.750 | 24 | <0.001 | |
a Abbreviations: Df, Degree of freedom; K-S, Kolmogorov-Smirnov; SD, Standard deviation; SEM, Standard error of mean; TSH, Thyroid stimulating hormone
Z Skewness = Skewness-0 / SE Skewness and Z Kurtosis = Kurtosis-0 / SE Kurtosis .
An absolute value of the score greater than 1.96 or lesser than -1.96 is significant at P < 0.05, while greater than 2.58 or lesser than -2.58 is significant at P < 0.01, and greater than 3.29 or lesser than -3.29 is significant at P < 0.001. In small samples, values greater or lesser than 1.96 are sufficient to establish normality of the data. However, in large samples (200 or more) with small standard errors, this criterion should be changed to ± 2.58 and in very large samples no criterion should be applied (that is, significance tests of skewness and kurtosis should not be used) ( 2 ). Results presented in Table indicate that parametric statistics should be used for serum magnesium data and non-parametric statistics should be used for serum TSH data.
5. Conclusions
According to the available literature, assessing the normality assumption should be taken into account for using parametric statistical tests. It seems that the most popular test for normality, that is, the K-S test, should no longer be used owing to its low power. It is preferable that normality be assessed both visually and through normality tests, of which the Shapiro-Wilk test, provided by the SPSS software, is highly recommended. The normality assumption also needs to be considered for validation of data presented in the literature as it shows whether correct statistical tests have been used.
Acknowledgments
The authors thank Ms. N. Shiva for critical editing of the manuscript for English grammar and syntax and Dr. F. Hosseinpanah for statistical comments.
Implication for health policy/practice/research/medical education: Data presented in this article could help for the selection of appropriate statistical analyses based on the distribution of data.
Please cite this paper as: Ghasemi A, Zahediasl S. Normality Tests for Statistical Analysis: A Guide for Non-Statisticians. Int J Endocrinol Metab. 2012;10(2):486-9. DOI: 10.5812/ijem.3505
Financial Disclosure: None declared.
Funding/Support: None declared.
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
How do the t-distribution and standard normal distribution differ, and why is t-distribution used more?
For statistical inference (e.g., hypothesis testing or computing confidence intervals), why do we use the t-distribution instead of the standard normal distribution? My class started with the standard normal distribution and shifted to the t-distribution, and I am not fully sure why. Is it because t-distributions can a) deal with small sample sizes (because it gives more emphasis to the tails) or b) be more robust to a non-normally distributed sample?
- hypothesis-testing
- mathematical-statistics
- confidence-interval
- t-distribution
- $\begingroup$ Possibly related: stats.stackexchange.com/questions/285649/… $\endgroup$ – Henry Commented Aug 22, 2018 at 23:09
- $\begingroup$ Searcher like stats.stackexchange.com/search?q=t-distribution+normal and stats.stackexchange.com/search?q=t-test+normal will include a number of relevant posts (and a lot of other hits so you may need to add further keywords to reduce the clutter). $\endgroup$ – Glen_b Commented Aug 23, 2018 at 2:18
2 Answers 2
The normal distribution (which is almost certainly returning in later chapters of your course) is much easier to motivate than the t distribution for students new to the material. The reason why you are learning about the t distribution is more or less for your first reason: the t distribution takes a single parameter—sample size minus one—and more correctly accounts for uncertainty due to (small) sample size than the normal distribution when making inferences about a sample mean of normally-distributed data, assuming that the true variance is unknown.
With increasing sample size, both t and standard normal distributions are both approximately as robust with respect to deviations from normality (as sample size increases the t distribution converges to the standard normal distribution). Nonparametric tests (which I start teaching about half way through my intro stats course) are generally much more robust to non-normality than either t or normal distributions.
Finally, you are likely going to learn tests and confidence intervals for many different distributions by the end of your course ( F , $\chi^{2}$, rank distributions—at least in their table p -values, for example).
- 3 $\begingroup$ Thank you so much for this awesome response. I now get that t-distributions can better account for small sample sizes. However, if the sample size is large (> 30), it doesn't matter whether we use a t or standard normal distribution, right? $\endgroup$ – Jane Sully Commented Aug 22, 2018 at 19:26
- 2 $\begingroup$ they become very similar when the degrees of freedom rise. $\endgroup$ – Bernhard Commented Aug 22, 2018 at 19:37
- 2 $\begingroup$ @JaneSully Sure, but, for inference about means of normal data, it is never wrong to use the t distribution. $\endgroup$ – Alexis Commented Aug 22, 2018 at 21:13
- 1 $\begingroup$ (Also, when/if you like an answer enough to say that it has answered your question, you can "accept" it by clicking on the check mark to the top left of the question. :). $\endgroup$ – Alexis Commented Aug 22, 2018 at 21:24
- 2 $\begingroup$ I disagree with this statement: "the t distribution takes a single parameter—sample size minus one—and more correctly accounts for uncertainty due to (small) sample size than the normal distribution when making inferences about a sample mean of normally-distributed data." E.g. see this lecture: onlinecourses.science.psu.edu/stat414/node/173 There's no need for t-distribution on Gaussian data when standard deviation is known. The key here is whether you do or do not know the variance, not the n-1 adjustment $\endgroup$ – Aksakal Commented Aug 23, 2018 at 3:49
The reason t-distribution is used in inference instead of normal is due to the fact that the theoretical distribution of some estimators is normal (Gaussian) only when the standard deviation is known, and when it is unknown the theoretical distribution is Student t.
We rarely know the standard deviation. Usually, we estimate from the sample, so for many estimators it is theoretically more solid to use Student t distribution and not normal.
Some estimators are consistent, i.e. in layman terms, they get better when the sample size increases. Student t becomes normal when sample size is large.
Example: sample mean
Consider a mean $\mu$ of the sample $x_1,x_2,\dots,x_n$. We can estimate it using a usual average estimator: $\bar x=\frac 1 n\sum_{i=1}^nx_i$, which you may call a sample mean.
If we want to make inference statements about the mean, such as whether a true mean $\mu<0$, we can use the sample mean $\bar x$ but we need to know what is its distribution. It turns out that if we knew the standard deviation $\sigma$ of $x_i$, then the sample mean would be distributed around the true mean according to Gaussian: $\bar x\sim\mathcal N(\mu,\sigma^2/n)$, for large enough $n$
The problem's that we rarely know $\sigma$, but we can estimate its value from the sample $\hat\sigma$ using one of the estimators. In this case the distribution of the sample mean is no longer Gaussian , but closer to Student t distribution.
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged hypothesis-testing mathematical-statistics confidence-interval inference t-distribution or ask your own question .
- Featured on Meta
- We've made changes to our Terms of Service & Privacy Policy - July 2024
- Bringing clarity to status tag usage on meta sites
Hot Network Questions
- How to make outhouses less icky?
- python stats.spearmanr and R cor.test(method='spearman') don't return the same p-value?
- In the US, can I buy iPhone and Android phones and claim them as expense?
- block-structure matrix
- Fitting 10 pieces of pizza in a box
- How does a 0-conf signature bond work?
- SF novel where the story, or part of it, is narrated by two linked brains taking turns
- "Knocking it out of the park" sports metaphor American English vs British English?
- How can flyby missions work?
- Calling get_GeodesicArea from ogr2ogr
- Can a "sharp turn" on a trace with an SMD resistor also present a risk of reflection?
- How to raise a vector to powers contained in a vector, change the list into a product, and do this for all the lines of a matrix, efficiently?
- What is the difference between an `.iso` OS for a network and an `.iso` OS for CD?
- Reference request: "Higher order eigentuples" as generalized eigenvectors?
- Why is global state hard to test? Doesn't setting the global state at the beginning of each test solve the problem?
- Why do combinatorists care about Kazhdan–Lusztig polynomials?
- Why do only 2 USB cameras work while 4 USB cameras cannot stream at once?
- Would it take less thrust overall to put an object into higher orbit?
- Can I use rear (thru) axle with crack for a few rides, before getting a new one?
- Who gave God the name 'Jealous' as referred to in Exodus 34:14?
- How to remove files which confirm to a certain number pattern
- Retroactively specifying `-only` or `-or-later` for GPLv2 in an adopted project
- Unit fractions summing to 1 - proving upper bound for the denominators.
- Is it OK to use the same field in the database to store both a percentage rate and a fixed money fee?

IMAGES
COMMENTS
Step 3. Assuming the null hypothesis to be true, define the test statistic, usually. Step 4. Calculate either the critical value (s) or the p - value (probability of the observed value) for the test. Step 5. Compare the observed value of the test statistic with the critical value (s) or the p - value with the significance level.
When testing a single population proportion use a normal test for a single population proportion if the data comes from a simple, random sample, fill the requirements for a binomial distribution, and the mean number of successes and the mean number of failures satisfy the conditions: \(np > 5\) and \(nq > 5\) where \(n\) is the sample size, \(p ...
When to do a Normal Hypothesis Test. There are two types of hypothesis tests you need to know about: binomial distribution hypothesis tests and normal distribution hypothesis tests.In binomial hypothesis tests, you are testing the probability parameter p.In normal hypothesis tests, you are testing the mean parameter \mu.This gives us a key difference that we can use to determine what test to ...
Step 1: Check assumptions and write hypotheses. The assumption here is that the sampling distribution is approximately normal. From the given StatKey output, the randomization distribution is approximately normal. \ (H_0\colon p=0.50\) \ (H_a\colon p>0.50\) 2. Calculate the test statistic.
The alternative hypothesis will be that $\mu > 25$ because this is what we have been asked to test. \begin{align} &H_0:\mu=25. \\ &H_1:\mu>25. \end{align} Now we need to calculate the test statistic. We start with the assumption the normal distribution is still valid. This is because the null hypothesis states there is no change in $\mu$.
A normal distribution is a probability distribution that is symmetric about the mean, indicating that data near the mean are more likely to occur than data far from it. In graph form, a normal distribution appears as a bell curve. The values in the x-axis of the normal distribution graph represent the z-scores. The test statistic that you wish ...
A statistical hypothesis test is a method of statistical inference used to decide whether the data sufficiently supports a particular hypothesis. ... [C α, ∞) is realized as the tail of the standard normal distribution. Critical value s of a statistical test are the boundaries of the acceptance region of the test. [41]
Distribution Needed for Hypothesis Testing. In order for a hypothesis test's results to be generalized to a population, certain requirements must be satisfied. When testing for a single population mean: ... The normal test will work if the data come from a simple, random sample and the population is approximately normally distributed, or the ...
We must take a look at the sampling distribution of sample proportions and we hope that it is approximately normal. In our sample, we spin a penny 100 times and it lands tails side up 67 times. This is the number of observed successes in the sample. What is the number of expected successes in our sample (assuming our null hypothesis is true)?
For a conjectured μ0 ∈ R, define the test statistic Z = M − μ0 σ /√n. If μ = μ0 then Z has the standard normal distribution. If μ ≠ μ0 then Z has the normal distribution with mean μ − μ0 σ / √n and variance 1. So in case (b), μ − μ0 σ / √n can be viewed as a non-centrality parameter.
Assumptions. When you perform a hypothesis test of a single population mean μ using a normal distribution (often called a z-test), you take a simple random sample from the population. The population you are testing is normally distributed, or your sample size is sufficiently large.You know the value of the population standard deviation, which, in reality, is rarely known.
The normal distribution is a continuous probability distribution that is symmetrical around its mean with most values near the central peak. ... If you be able to trust the hypothesis testing (p-values, CIs), the residuals should be normally distributed. If they're not normally distributed, you can't trust those results. ...
With a very large sample, you can even get a p-value of less than 0.05, rejecting the null hypothesis of normal distribution. To avoid this problem, graphical methods are increasingly being used. Graphical test for normal distribution. ... Then, just click on Test Normal Distribution and you will get the results. Furthermore, if you are ...
One sample z-test . Assume data are independently sampled from a normal distribution with unknown mean μ and known variance σ 2 = 9. Make an initial assumption that μ = 65. Specify the hypothesis: H 0: μ = 65 H A: μ ≠ 65. z-statistic: 3.58. z-statistic follow N(0,1) distribution
Hypothesis testing. Hypothesis testing guide; Null vs. alternative hypotheses; Statistical significance; p value; Type I & Type II errors; Statistical power; ... The normal distribution is a probability distribution, so the total area under the curve is always 1 or 100%. The formula for the normal probability density function looks fairly ...
Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test. Step 4: Decide whether to reject or fail to reject your null hypothesis. Step 5: Present your findings. Other interesting articles. Frequently asked questions about hypothesis testing.
Earlier in the course, we discussed sampling distributions. Particular distributions are associated with hypothesis testing. Perform tests of a population mean using a normal distribution or a Student's t-distribution. (Remember, use a Student's t-distribution when the population standard deviation is unknown and the distribution of the sample mean is approximately normal.)
During a hypothesis test, we work to know if a sample statistic is unusual or not. Therefore, we must think about probabilities from a sampling distribution. ... In the second step of a hypothesis test, we verify that the sampling distribution is approximately normal and we identify or compute any sample statistics. Step 3: Assess the Evidence.
Hypothesis Testing (Normal Distribution) 1. You set up the null hypothesis H 0 against an alternative hypothesis H A. H 0: μ = μ 0 against H a: μ > μ 0 (possibly H a: μ < μ 0, H a: μ ≠ μ 0 ). 2. Then, you do an experiment and find that the average value is x. Next, you calculate the probability P ( X ≥ x) for the alternative ...
The hypothesis test will follow the same six steps we learned in the previous Lesson although they are not explicitly stated. We will use the sampling distribution of \(\hat{p}_1-\hat{p}_2\) as we did for the confidence interval. ... will follow a standard normal distribution. Finally, we can develop our hypothesis test for \(p_1-p_2\). Null ...
Definition (Normal Distribution) The normal distributions are a family of distribution curves. Each member of the family is specified by two parameters: the standard deviation, denoted by σ. normal distribution follows a bell-shaped curve. For shorthand we often use the notation N (μ, σ) to specify a normal distribution with parameters μ ...
5.1 Bayes Factors for Testing a Normal Mean: variance known. Now we show how to obtain Bayes factors for testing hypothesis about a normal mean, where the variance is known.To start, let's consider a random sample of observations from a normal population with mean \(\mu\) and pre-specified variance \(\sigma^2\).We consider testing whether the population mean \(\mu\) is equal to \(m_0\) or not.
The Shapiro Wilk test is the most powerful test when testing for a normal distribution. 6.2. Interpretation. If the P-Value of the Shapiro Wilk Test is larger than 0.05, we assume a normal distribution; If the P-Value of the Shapiro Wilk Test is smaller than 0.05, we do not assume a normal distribution; 6.3. Implementation
A statistics instructor thinks the mean score is higher than 65. He samples ten statistics students and obtains the scores 65 65 70 67 66 63 63 68 72 71. He performs a hypothesis test using a 5% level of significance. The data are assumed to be from a normal distribution. Answer. Set up the hypothesis test:
The tests mentioned above compare the scores in the sample to a normally distributed set of scores with the same mean and standard deviation; the null hypothesis is that "sample distribution is normal." If the test is significant, the distribution is non-normal.
The normal distribution (which is almost certainly returning in later chapters of your course) is much easier to motivate than the t distribution for students new to the material. The reason why you are learning about the t distribution is more or less for your first reason: the t distribution takes a single parameter—sample size minus one—and more correctly accounts for uncertainty due to ...
When testing a single population proportion use a normal test for a single population proportion if the data comes from a simple, random sample, fill the requirements for a binomial distribution, and the mean number of successes and the mean number of failures satisfy the conditions: \(np > 5\) and \(nq > 5\) where \(n\) is the sample size, \(p ...