hypothesis test level of significance

Quality Improvement
Talk To Minitab

Understanding Hypothesis Tests: Significance Levels (Alpha) and P values in Statistics

Topics: Hypothesis Testing , Statistics

What do significance levels and P values mean in hypothesis tests? What is statistical significance anyway? In this post, I’ll continue to focus on concepts and graphs to help you gain a more intuitive understanding of how hypothesis tests work in statistics.

To bring it to life, I’ll add the significance level and P value to the graph in my previous post in order to perform a graphical version of the 1 sample t-test. It’s easier to understand when you can see what statistical significance truly means!

Here’s where we left off in my last post . We want to determine whether our sample mean (330.6) indicates that this year's average energy cost is significantly different from last year’s average energy cost of $260.

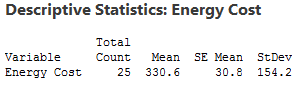
The probability distribution plot above shows the distribution of sample means we’d obtain under the assumption that the null hypothesis is true (population mean = 260) and we repeatedly drew a large number of random samples.

I left you with a question: where do we draw the line for statistical significance on the graph? Now we'll add in the significance level and the P value, which are the decision-making tools we'll need.

We'll use these tools to test the following hypotheses:

Null hypothesis: The population mean equals the hypothesized mean (260).
Alternative hypothesis: The population mean differs from the hypothesized mean (260).

What Is the Significance Level (Alpha)?

The significance level, also denoted as alpha or α, is the probability of rejecting the null hypothesis when it is true. For example, a significance level of 0.05 indicates a 5% risk of concluding that a difference exists when there is no actual difference.

These types of definitions can be hard to understand because of their technical nature. A picture makes the concepts much easier to comprehend!

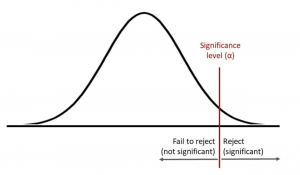
The significance level determines how far out from the null hypothesis value we'll draw that line on the graph. To graph a significance level of 0.05, we need to shade the 5% of the distribution that is furthest away from the null hypothesis.

Probability plot that shows the critical regions for a significance level of 0.05

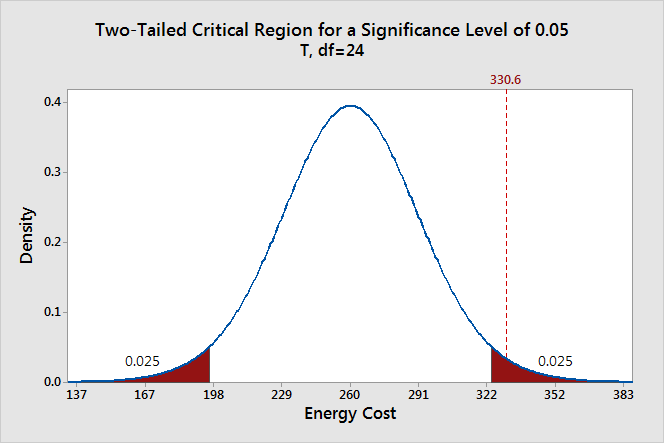
In the graph above, the two shaded areas are equidistant from the null hypothesis value and each area has a probability of 0.025, for a total of 0.05. In statistics, we call these shaded areas the critical region for a two-tailed test. If the population mean is 260, we’d expect to obtain a sample mean that falls in the critical region 5% of the time. The critical region defines how far away our sample statistic must be from the null hypothesis value before we can say it is unusual enough to reject the null hypothesis.

Our sample mean (330.6) falls within the critical region, which indicates it is statistically significant at the 0.05 level.

We can also see if it is statistically significant using the other common significance level of 0.01.

Probability plot that shows the critical regions for a significance level of 0.01

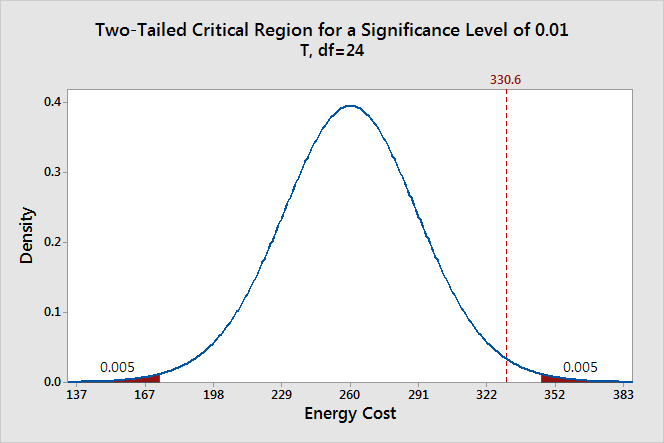
The two shaded areas each have a probability of 0.005, which adds up to a total probability of 0.01. This time our sample mean does not fall within the critical region and we fail to reject the null hypothesis. This comparison shows why you need to choose your significance level before you begin your study. It protects you from choosing a significance level because it conveniently gives you significant results!

Thanks to the graph, we were able to determine that our results are statistically significant at the 0.05 level without using a P value. However, when you use the numeric output produced by statistical software , you’ll need to compare the P value to your significance level to make this determination.

Ready for a demo of Minitab Statistical Software? Just ask!

What Are P values?

P-values are the probability of obtaining an effect at least as extreme as the one in your sample data, assuming the truth of the null hypothesis.

This definition of P values, while technically correct, is a bit convoluted. It’s easier to understand with a graph!

To graph the P value for our example data set, we need to determine the distance between the sample mean and the null hypothesis value (330.6 - 260 = 70.6). Next, we can graph the probability of obtaining a sample mean that is at least as extreme in both tails of the distribution (260 +/- 70.6).

Probability plot that shows the p-value for our sample mean

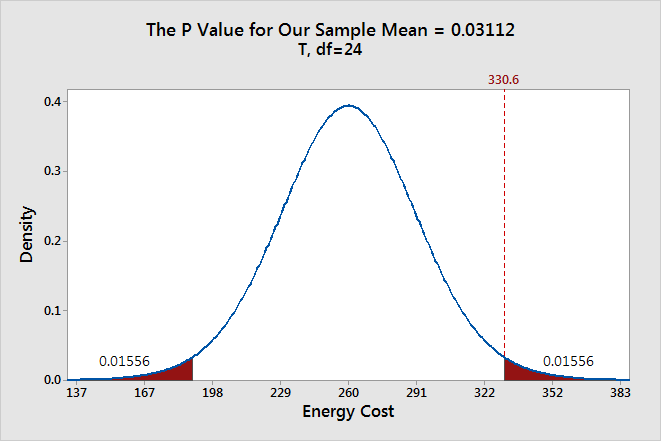
In the graph above, the two shaded areas each have a probability of 0.01556, for a total probability 0.03112. This probability represents the likelihood of obtaining a sample mean that is at least as extreme as our sample mean in both tails of the distribution if the population mean is 260. That’s our P value!

When a P value is less than or equal to the significance level, you reject the null hypothesis. If we take the P value for our example and compare it to the common significance levels, it matches the previous graphical results. The P value of 0.03112 is statistically significant at an alpha level of 0.05, but not at the 0.01 level.

If we stick to a significance level of 0.05, we can conclude that the average energy cost for the population is greater than 260.

A common mistake is to interpret the P-value as the probability that the null hypothesis is true. To understand why this interpretation is incorrect, please read my blog post How to Correctly Interpret P Values .

Discussion about Statistically Significant Results

A hypothesis test evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. A test result is statistically significant when the sample statistic is unusual enough relative to the null hypothesis that we can reject the null hypothesis for the entire population. “Unusual enough” in a hypothesis test is defined by:

The assumption that the null hypothesis is true—the graphs are centered on the null hypothesis value.
The significance level—how far out do we draw the line for the critical region?
Our sample statistic—does it fall in the critical region?

Keep in mind that there is no magic significance level that distinguishes between the studies that have a true effect and those that don’t with 100% accuracy. The common alpha values of 0.05 and 0.01 are simply based on tradition. For a significance level of 0.05, expect to obtain sample means in the critical region 5% of the time when the null hypothesis is true . In these cases, you won’t know that the null hypothesis is true but you’ll reject it because the sample mean falls in the critical region. That’s why the significance level is also referred to as an error rate!

This type of error doesn’t imply that the experimenter did anything wrong or require any other unusual explanation. The graphs show that when the null hypothesis is true, it is possible to obtain these unusual sample means for no reason other than random sampling error. It’s just luck of the draw.

Significance levels and P values are important tools that help you quantify and control this type of error in a hypothesis test. Using these tools to decide when to reject the null hypothesis increases your chance of making the correct decision.

If you like this post, you might want to read the other posts in this series that use the same graphical framework:

Previous: Why We Need to Use Hypothesis Tests
Next: Confidence Intervals and Confidence Levels

If you'd like to see how I made these graphs, please read: How to Create a Graphical Version of the 1-sample t-Test .

Trust Center

Terms of Use
Privacy Policy
Cookies Settings

Prompt Library
DS/AI Trends
Stats Tools
Interview Questions
Generative AI
Machine Learning
Deep Learning

Level of Significance & Hypothesis Testing

level of significance and hypothesis testing

In hypothesis testing , the level of significance is a measure of how confident you can be about rejecting the null hypothesis. This blog post will explore what hypothesis testing is and why understanding significance levels are important for your data science projects. In addition, you will also get to test your knowledge of level of significance towards the end of the blog with the help of quiz . These questions can help you test your understanding and prepare for data science / statistics interviews . Before we look into what level of significance is, let’s quickly understand what is hypothesis testing.

Table of Contents

What is Hypothesis testing and how is it related to significance level?

Hypothesis testing can be defined as tests performed to evaluate whether a claim or theory about something is true or otherwise. In order to perform hypothesis tests, the following steps need to be taken:

Hypothesis formulation: Formulate the null and alternate hypothesis
Data collection: Gather the sample of data
Statistical tests: Determine the statistical test and test statistics. The statistical tests can be z-test or t-test depending upon the number of data samples and/or whether the population variance is known otherwise.
Set the level of significance
Calculate the p-value
Draw conclusions: Based on the value of p-value and significance level, reject the null hypothesis or otherwise.

A detailed explanation is provided in one of my related posts titled hypothesis testing explained with examples .

What is the level of significance?

The level of significance is defined as the criteria or threshold value based on which one can reject the null hypothesis or fail to reject the null hypothesis. The level of significance determines whether the outcome of hypothesis testing is statistically significant or otherwise. The significance level is also called as alpha level.

Another way of looking at the level of significance is the value which represents the likelihood of making a type I error . You may recall that Type I error occurs while evaluating hypothesis testing outcomes. If you reject the null hypothesis by mistake, you end up making a Type I error. This scenario is also termed as “false positive”. Take an example of a person alleged with committing a crime. The null hypothesis is that the person is not guilty. Type I error happens when you reject the null hypothesis by mistake. Given the example, a Type I error happens when you reject the null hypothesis that the person is not guilty by mistake. The innocent person is convicted.

The level of significance can take values such as 0.1 , 0.05 , 0.01 . The most common value of the level of significance is 0.05 . The lower the value of significance level, the lesser is the chance of type I error. That would essentially mean that the experiment or hypothesis testing outcome would really need to be highly precise for one to reject the null hypothesis. The likelihood of making a type I error would be very low. However, that does increase the chances of making type II errors as you may make mistakes in failing to reject the null hypothesis. You may want to read more details in relation to type I errors and type II errors in this post – Type I errors and Type II errors in hypothesis testing

The outcome of the hypothesis testing is evaluated with the help of a p-value. If the p-value is less than the level of significance, then the hypothesis testing outcome is statistically significant. On the other hand, if the hypothesis testing outcome is not statistically significant or the p-value is more than the level of significance, then we fail to reject the null hypothesis. The same is represented in the picture below for a right-tailed test. I will be posting details on different types of tail test in future posts.

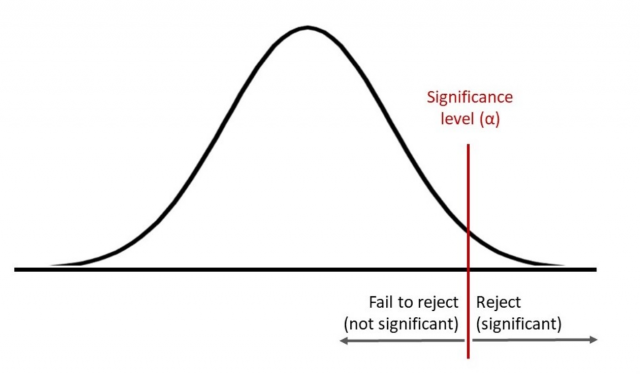
The picture below represents the concept for two-tailed hypothesis test:

level of significance and two-tailed test

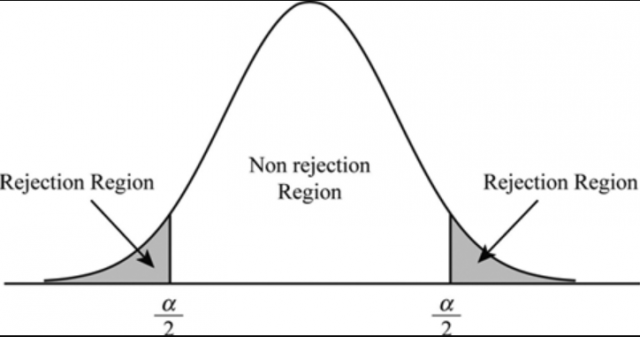
For example: Let’s say that a school principal wants to find out whether extra coaching of 2 hours after school help students do better in their exams. The hypothesis would be as follows:

Null hypothesis : There is no difference between the performance of students even after providing extra coaching of 2 hours after the schools are over.
Alternate hypothesis : Students perform better when they get extra coaching of 2 hours after the schools are over. This hypothesis testing example would require a level of significant value at 0.05 or simply put, it would need to be highly precise that there’s actually a difference between the performance of students based on whether they take extra coaching.

Now, let’s say that we conduct this experiment with 100 students and measure their scores in exams. The test statistics is computed to be z=-0.50 (p-value=0.62). Since the p-value is more than 0.05, we fail to reject the null hypothesis. There is not enough evidence to show that there’s a difference in the performance of students based on whether they get extra coaching.

While performing hypothesis tests or experiments, it is important to keep the level of significance in mind.

Why does one need a level of significance?

In hypothesis tests, if we do not have some sort of threshold by which to determine whether your results are statistically significant enough for you to reject the null hypothesis, then it would be tough for us to determine whether your findings are significant or not. This is why we take into account levels of significance when performing hypothesis tests and experiments.

Since hypothesis testing helps us in making decisions about our data, having a level of significance set up allows one to know what sort of chances their findings might have of actually being due to the null hypothesis. If you set your level of significance at 0.05 for example, it would mean that there’s only a five percent chance that the difference between groups (assuming two groups are tested) is due to random sampling error. So if we found a difference in the performance of students based on whether they take extra coaching, we would need to consider other factors that could have contributed to the difference.

This is why hypothesis testing and level of significance go hand in hand with one another: hypothesis tests help us know whether our data falls within a certain range where it’s statistically significant or not so statistically significant whereas the level of significance tells us how likely is it that our hypothesis testing results are not due to random sampling error.

How is the level of significance used in hypothesis testing?

The level of significance along with the test statistic and p-value formed a key part of hypothesis testing. The value that you derive from hypothesis testing depends on whether or not you accept/reject the null hypothesis, given your findings at each step. Before going into rejection vs non-rejection, let’s understand the terms better.

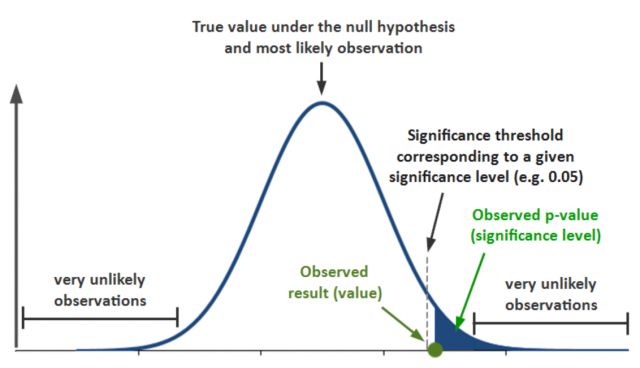
If the test statistic falls within the critical region, you reject the null hypothesis. This means that your findings are statistically significant and support the alternate hypothesis. The value of the p-value determines how likely it is for finding this outcome if, in fact, the null hypothesis were true. If the p-value is less than or equal to the level of significance, you reject the null hypothesis. This means that your hypothesis testing outcome was statistically significant at a certain degree and in favor of the alternate hypothesis.

If on the other hand, the p-value is greater than alpha level or significance level, then you fail to reject the null hypothesis. These findings are not statistically significant enough for one to reject the null hypothesis. The same is represented in the diagram below:

Level of Significance – Quiz / Interview Questions

Here are some practice questions which can help you in testing your questions, and, also prepare for interviews.

#1. The statistically significant outcome of hypothesis testing would mean which of the following?

#2. the p-value of 0.03 is statistically significant for significance level as 0.01, #3. which of the following is looks to be inappropriate level of significance, #4. which one of the following is considered most popular choice of significance level, #5. which of the following will result in greater type ii error, #6. the p-value less than the level of significance would mean which of the following, #7. which of the following will result in greater type i error, #8. level of significance is also called as ________, recent posts.

Completion Model vs Chat Model: Python Examples - June 30, 2024
LLM Hosting Strategy, Options & Cost: Examples - June 30, 2024
Application Architecture for LLM Applications: Examples - June 25, 2024

Oops! Check your answers again. The minimum pass percentage is 70%.

Hypothesis testing is an important statistical concept that helps us determine whether the claim made about anything is true or otherwise. The hypothesis test statistic, level of significance, and p-value all work together to help you make decisions about your data. If our hypothesis tests show enough evidence to reject the null hypothesis, then we know statistically significant findings are at hand. This post gave you ideas for how you can use hypothesis testing in your experiments by understanding what it means when someone rejects or fails to reject the null hypothesis.

Ajitesh Kumar

3 responses.

Well explained with examples and helpful illustration

Thank you for your feedback

Well explained

ChatGPT Prompts (250+)

Generate Design Ideas for App
Expand Feature Set of App
Create a User Journey Map for App
Generate Visual Design Ideas for App
Generate a List of Competitors for App
Completion Model vs Chat Model: Python Examples
LLM Hosting Strategy, Options & Cost: Examples
Application Architecture for LLM Applications: Examples
Python Pickle Security Issues / Risk
Pricing Analytics in Banking: Strategies, Examples

Data Science / AI Trends

• Prepend any arxiv.org link with talk2 to load the paper into a responsive chat application
• Custom LLM and AI Agents (RAG) On Structured + Unstructured Data - AI Brain For Your Organization
• Guides, papers, lecture, notebooks and resources for prompt engineering
• Common tricks to make LLMs efficient and stable
• Machine learning in finance

Free Online Tools

Create Scatter Plots Online for your Excel Data
Histogram / Frequency Distribution Creation Tool
Online Pie Chart Maker Tool
Z-test vs T-test Decision Tool
Independent samples t-test calculator

StatPearls [Internet].

Hypothesis testing, p values, confidence intervals, and significance.

Jacob Shreffler ; Martin R. Huecker .

Affiliations

Last Update: March 13, 2023 .

Definition/Introduction

Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting these findings, which may affect the adequate application of the data.

Issues of Concern

Without a foundational understanding of hypothesis testing, p values, confidence intervals, and the difference between statistical and clinical significance, it may affect healthcare providers' ability to make clinical decisions without relying purely on the research investigators deemed level of significance. Therefore, an overview of these concepts is provided to allow medical professionals to use their expertise to determine if results are reported sufficiently and if the study outcomes are clinically appropriate to be applied in healthcare practice.

Hypothesis Testing

Investigators conducting studies need research questions and hypotheses to guide analyses. Starting with broad research questions (RQs), investigators then identify a gap in current clinical practice or research. Any research problem or statement is grounded in a better understanding of relationships between two or more variables. For this article, we will use the following research question example:

Research Question: Is Drug 23 an effective treatment for Disease A?

Research questions do not directly imply specific guesses or predictions; we must formulate research hypotheses. A hypothesis is a predetermined declaration regarding the research question in which the investigator(s) makes a precise, educated guess about a study outcome. This is sometimes called the alternative hypothesis and ultimately allows the researcher to take a stance based on experience or insight from medical literature. An example of a hypothesis is below.

Research Hypothesis: Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22.

The null hypothesis states that there is no statistical difference between groups based on the stated research hypothesis.

Researchers should be aware of journal recommendations when considering how to report p values, and manuscripts should remain internally consistent.

Regarding p values, as the number of individuals enrolled in a study (the sample size) increases, the likelihood of finding a statistically significant effect increases. With very large sample sizes, the p-value can be very low significant differences in the reduction of symptoms for Disease A between Drug 23 and Drug 22. The null hypothesis is deemed true until a study presents significant data to support rejecting the null hypothesis. Based on the results, the investigators will either reject the null hypothesis (if they found significant differences or associations) or fail to reject the null hypothesis (they could not provide proof that there were significant differences or associations).

To test a hypothesis, researchers obtain data on a representative sample to determine whether to reject or fail to reject a null hypothesis. In most research studies, it is not feasible to obtain data for an entire population. Using a sampling procedure allows for statistical inference, though this involves a certain possibility of error. [1] When determining whether to reject or fail to reject the null hypothesis, mistakes can be made: Type I and Type II errors. Though it is impossible to ensure that these errors have not occurred, researchers should limit the possibilities of these faults. [2]

Significance

Significance is a term to describe the substantive importance of medical research. Statistical significance is the likelihood of results due to chance. [3] Healthcare providers should always delineate statistical significance from clinical significance, a common error when reviewing biomedical research. [4] When conceptualizing findings reported as either significant or not significant, healthcare providers should not simply accept researchers' results or conclusions without considering the clinical significance. Healthcare professionals should consider the clinical importance of findings and understand both p values and confidence intervals so they do not have to rely on the researchers to determine the level of significance. [5] One criterion often used to determine statistical significance is the utilization of p values.

P values are used in research to determine whether the sample estimate is significantly different from a hypothesized value. The p-value is the probability that the observed effect within the study would have occurred by chance if, in reality, there was no true effect. Conventionally, data yielding a p<0.05 or p<0.01 is considered statistically significant. While some have debated that the 0.05 level should be lowered, it is still universally practiced. [6] Hypothesis testing allows us to determine the size of the effect.

An example of findings reported with p values are below:

Statement: Drug 23 reduced patients' symptoms compared to Drug 22. Patients who received Drug 23 (n=100) were 2.1 times less likely than patients who received Drug 22 (n = 100) to experience symptoms of Disease A, p<0.05.

Statement:Individuals who were prescribed Drug 23 experienced fewer symptoms (M = 1.3, SD = 0.7) compared to individuals who were prescribed Drug 22 (M = 5.3, SD = 1.9). This finding was statistically significant, p= 0.02.

For either statement, if the threshold had been set at 0.05, the null hypothesis (that there was no relationship) should be rejected, and we should conclude significant differences. Noticeably, as can be seen in the two statements above, some researchers will report findings with < or > and others will provide an exact p-value (0.000001) but never zero [6] . When examining research, readers should understand how p values are reported. The best practice is to report all p values for all variables within a study design, rather than only providing p values for variables with significant findings. [7] The inclusion of all p values provides evidence for study validity and limits suspicion for selective reporting/data mining.

While researchers have historically used p values, experts who find p values problematic encourage the use of confidence intervals. [8] . P-values alone do not allow us to understand the size or the extent of the differences or associations. [3] In March 2016, the American Statistical Association (ASA) released a statement on p values, noting that scientific decision-making and conclusions should not be based on a fixed p-value threshold (e.g., 0.05). They recommend focusing on the significance of results in the context of study design, quality of measurements, and validity of data. Ultimately, the ASA statement noted that in isolation, a p-value does not provide strong evidence. [9]

When conceptualizing clinical work, healthcare professionals should consider p values with a concurrent appraisal study design validity. For example, a p-value from a double-blinded randomized clinical trial (designed to minimize bias) should be weighted higher than one from a retrospective observational study [7] . The p-value debate has smoldered since the 1950s [10] , and replacement with confidence intervals has been suggested since the 1980s. [11]

Confidence Intervals

A confidence interval provides a range of values within given confidence (e.g., 95%), including the accurate value of the statistical constraint within a targeted population. [12] Most research uses a 95% CI, but investigators can set any level (e.g., 90% CI, 99% CI). [13] A CI provides a range with the lower bound and upper bound limits of a difference or association that would be plausible for a population. [14] Therefore, a CI of 95% indicates that if a study were to be carried out 100 times, the range would contain the true value in 95, [15] confidence intervals provide more evidence regarding the precision of an estimate compared to p-values. [6]

In consideration of the similar research example provided above, one could make the following statement with 95% CI:

Statement: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22; there was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

It is important to note that the width of the CI is affected by the standard error and the sample size; reducing a study sample number will result in less precision of the CI (increase the width). [14] A larger width indicates a smaller sample size or a larger variability. [16] A researcher would want to increase the precision of the CI. For example, a 95% CI of 1.43 – 1.47 is much more precise than the one provided in the example above. In research and clinical practice, CIs provide valuable information on whether the interval includes or excludes any clinically significant values. [14]

Null values are sometimes used for differences with CI (zero for differential comparisons and 1 for ratios). However, CIs provide more information than that. [15] Consider this example: A hospital implements a new protocol that reduced wait time for patients in the emergency department by an average of 25 minutes (95% CI: -2.5 – 41 minutes). Because the range crosses zero, implementing this protocol in different populations could result in longer wait times; however, the range is much higher on the positive side. Thus, while the p-value used to detect statistical significance for this may result in "not significant" findings, individuals should examine this range, consider the study design, and weigh whether or not it is still worth piloting in their workplace.

Similarly to p-values, 95% CIs cannot control for researchers' errors (e.g., study bias or improper data analysis). [14] In consideration of whether to report p-values or CIs, researchers should examine journal preferences. When in doubt, reporting both may be beneficial. [13] An example is below:

Reporting both: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22, p = 0.009. There was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

Clinical Significance

Recall that clinical significance and statistical significance are two different concepts. Healthcare providers should remember that a study with statistically significant differences and large sample size may be of no interest to clinicians, whereas a study with smaller sample size and statistically non-significant results could impact clinical practice. [14] Additionally, as previously mentioned, a non-significant finding may reflect the study design itself rather than relationships between variables.

Healthcare providers using evidence-based medicine to inform practice should use clinical judgment to determine the practical importance of studies through careful evaluation of the design, sample size, power, likelihood of type I and type II errors, data analysis, and reporting of statistical findings (p values, 95% CI or both). [4] Interestingly, some experts have called for "statistically significant" or "not significant" to be excluded from work as statistical significance never has and will never be equivalent to clinical significance. [17]

The decision on what is clinically significant can be challenging, depending on the providers' experience and especially the severity of the disease. Providers should use their knowledge and experiences to determine the meaningfulness of study results and make inferences based not only on significant or insignificant results by researchers but through their understanding of study limitations and practical implications.

Nursing, Allied Health, and Interprofessional Team Interventions

All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts in this chapter. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care.

Review Questions
Access free multiple choice questions on this topic.
Comment on this article.

Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.

Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

Cite this Page Shreffler J, Huecker MR. Hypothesis Testing, P Values, Confidence Intervals, and Significance. [Updated 2023 Mar 13]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

Bulk download StatPearls data from FTP

Related information

PMC PubMed Central citations
PubMed Links to PubMed

Recent Activity

Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearl... Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

Hypothesis Testing (cont...)

Hypothesis testing, the null and alternative hypothesis.

In order to undertake hypothesis testing you need to express your research hypothesis as a null and alternative hypothesis. The null hypothesis and alternative hypothesis are statements regarding the differences or effects that occur in the population. You will use your sample to test which statement (i.e., the null hypothesis or alternative hypothesis) is most likely (although technically, you test the evidence against the null hypothesis). So, with respect to our teaching example, the null and alternative hypothesis will reflect statements about all statistics students on graduate management courses.

The null hypothesis is essentially the "devil's advocate" position. That is, it assumes that whatever you are trying to prove did not happen ( hint: it usually states that something equals zero). For example, the two different teaching methods did not result in different exam performances (i.e., zero difference). Another example might be that there is no relationship between anxiety and athletic performance (i.e., the slope is zero). The alternative hypothesis states the opposite and is usually the hypothesis you are trying to prove (e.g., the two different teaching methods did result in different exam performances). Initially, you can state these hypotheses in more general terms (e.g., using terms like "effect", "relationship", etc.), as shown below for the teaching methods example:

Null Hypotheses (H ):	Undertaking seminar classes has no effect on students' performance.
Alternative Hypothesis (H ):	Undertaking seminar class has a positive effect on students' performance.

Depending on how you want to "summarize" the exam performances will determine how you might want to write a more specific null and alternative hypothesis. For example, you could compare the mean exam performance of each group (i.e., the "seminar" group and the "lectures-only" group). This is what we will demonstrate here, but other options include comparing the distributions , medians , amongst other things. As such, we can state:

Null Hypotheses (H ):	The mean exam mark for the "seminar" and "lecture-only" teaching methods is the same in the population.
Alternative Hypothesis (H ):	The mean exam mark for the "seminar" and "lecture-only" teaching methods is not the same in the population.

Now that you have identified the null and alternative hypotheses, you need to find evidence and develop a strategy for declaring your "support" for either the null or alternative hypothesis. We can do this using some statistical theory and some arbitrary cut-off points. Both these issues are dealt with next.

Significance levels

The level of statistical significance is often expressed as the so-called p -value . Depending on the statistical test you have chosen, you will calculate a probability (i.e., the p -value) of observing your sample results (or more extreme) given that the null hypothesis is true . Another way of phrasing this is to consider the probability that a difference in a mean score (or other statistic) could have arisen based on the assumption that there really is no difference. Let us consider this statement with respect to our example where we are interested in the difference in mean exam performance between two different teaching methods. If there really is no difference between the two teaching methods in the population (i.e., given that the null hypothesis is true), how likely would it be to see a difference in the mean exam performance between the two teaching methods as large as (or larger than) that which has been observed in your sample?

So, you might get a p -value such as 0.03 (i.e., p = .03). This means that there is a 3% chance of finding a difference as large as (or larger than) the one in your study given that the null hypothesis is true. However, you want to know whether this is "statistically significant". Typically, if there was a 5% or less chance (5 times in 100 or less) that the difference in the mean exam performance between the two teaching methods (or whatever statistic you are using) is as different as observed given the null hypothesis is true, you would reject the null hypothesis and accept the alternative hypothesis. Alternately, if the chance was greater than 5% (5 times in 100 or more), you would fail to reject the null hypothesis and would not accept the alternative hypothesis. As such, in this example where p = .03, we would reject the null hypothesis and accept the alternative hypothesis. We reject it because at a significance level of 0.03 (i.e., less than a 5% chance), the result we obtained could happen too frequently for us to be confident that it was the two teaching methods that had an effect on exam performance.

Whilst there is relatively little justification why a significance level of 0.05 is used rather than 0.01 or 0.10, for example, it is widely used in academic research. However, if you want to be particularly confident in your results, you can set a more stringent level of 0.01 (a 1% chance or less; 1 in 100 chance or less).

One- and two-tailed predictions

When considering whether we reject the null hypothesis and accept the alternative hypothesis, we need to consider the direction of the alternative hypothesis statement. For example, the alternative hypothesis that was stated earlier is:

Alternative Hypothesis (H ):

Undertaking seminar classes has a positive effect on students' performance.

The alternative hypothesis tells us two things. First, what predictions did we make about the effect of the independent variable(s) on the dependent variable(s)? Second, what was the predicted direction of this effect? Let's use our example to highlight these two points.

Sarah predicted that her teaching method (independent variable: teaching method), whereby she not only required her students to attend lectures, but also seminars, would have a positive effect (that is, increased) students' performance (dependent variable: exam marks). If an alternative hypothesis has a direction (and this is how you want to test it), the hypothesis is one-tailed. That is, it predicts direction of the effect. If the alternative hypothesis has stated that the effect was expected to be negative, this is also a one-tailed hypothesis.

Alternatively, a two-tailed prediction means that we do not make a choice over the direction that the effect of the experiment takes. Rather, it simply implies that the effect could be negative or positive. If Sarah had made a two-tailed prediction, the alternative hypothesis might have been:

Alternative Hypothesis (H ):

Undertaking seminar classes has an effect on students' performance.

In other words, we simply take out the word "positive", which implies the direction of our effect. In our example, making a two-tailed prediction may seem strange. After all, it would be logical to expect that "extra" tuition (going to seminar classes as well as lectures) would either have a positive effect on students' performance or no effect at all, but certainly not a negative effect. However, this is just our opinion (and hope) and certainly does not mean that we will get the effect we expect. Generally speaking, making a one-tail prediction (i.e., and testing for it this way) is frowned upon as it usually reflects the hope of a researcher rather than any certainty that it will happen. Notable exceptions to this rule are when there is only one possible way in which a change could occur. This can happen, for example, when biological activity/presence in measured. That is, a protein might be "dormant" and the stimulus you are using can only possibly "wake it up" (i.e., it cannot possibly reduce the activity of a "dormant" protein). In addition, for some statistical tests, one-tailed tests are not possible.

Rejecting or failing to reject the null hypothesis

Let's return finally to the question of whether we reject or fail to reject the null hypothesis.

If our statistical analysis shows that the significance level is below the cut-off value we have set (e.g., either 0.05 or 0.01), we reject the null hypothesis and accept the alternative hypothesis. Alternatively, if the significance level is above the cut-off value, we fail to reject the null hypothesis and cannot accept the alternative hypothesis. You should note that you cannot accept the null hypothesis, but only find evidence against it.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
Duis aute irure dolor in reprehenderit in voluptate
Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

5.1 - introduction to hypothesis testing.

Previously we used confidence intervals to estimate unknown population parameters. We compared confidence intervals to specified parameter values and when the specific value was contained in the interval, we concluded that there was not sufficient evidence of a difference between the population parameter and the specified value. In other words, any values within the confidence intervals were reasonable estimates of the population parameter and any values outside of the confidence intervals were not reasonable estimates. Here, we are going to look at a more formal method for testing whether a given value is a reasonable value of a population parameter. To do this we need to have a hypothesized value of the population parameter.

In this lesson we will compare data from a sample to a hypothesized parameter. In each case, we will compute the probability that a population with the specified parameter would produce a sample statistic as extreme or more extreme to the one we observed in our sample. This probability is known as the p-value and it is used to evaluate statistical significance.

A test is considered to be statistically significant when the p-value is less than or equal to the level of significance, also known as the alpha ($\alpha$) level. For this class, unless otherwise specified, $\alpha=0.05$; this is the most frequently used alpha level in many fields.

Sample statistics vary from the population parameter randomly. When results are statistically significant, we are concluding that the difference observed between our sample statistic and the hypothesized parameter is unlikely due to random sampling variation.

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

Knowledge Base

Hypothesis Testing | A Step-by-Step Guide with Easy Examples

Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.

There are 5 main steps in hypothesis testing:

State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a or H 1 ).
Collect data in a way designed to test the hypothesis.
Perform an appropriate statistical test .
Decide whether to reject or fail to reject your null hypothesis.
Present the findings in your results and discussion section.

Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.

Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.

After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.

The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.

H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.

Receive feedback on language, structure, and formatting

Professional editors proofread and edit your paper by focusing on:

Academic style
Vague sentences
Style consistency

See an example

For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.

There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).

If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.

Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.

Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .

an estimate of the difference in average height between the two groups.
a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.

Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.

In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.

In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .

In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.

In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.

However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.

If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”

These are superficial differences; you can see that they mean the same thing.

You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.

If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

Normal distribution
Descriptive statistics
Measures of central tendency
Correlation coefficient

Methodology

Cluster sampling
Stratified sampling
Types of interviews
Cohort study
Thematic analysis

Research bias

Implicit bias
Cognitive bias
Survivorship bias
Availability heuristic
Nonresponse bias
Regression to the mean

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved July 27, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/

Is this article helpful?

Rebecca Bevans

Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.

Back to blog home

Significance levels: what, why, and how, the statsig team.

In a world where data-driven decisions reign supreme, understanding statistical significance is like having a trusty compass to navigate the vast ocean of information. Just as a compass guides sailors to their destination, statistical significance helps researchers and analysts separate meaningful insights from random noise, ensuring they're on the right course.

Statistical significance is a crucial concept in data analysis, acting as a gatekeeper between coincidence and genuine patterns. It's the key to unlocking the true potential of your data, enabling you to make informed decisions with confidence.

Understanding significance levels

Statistical significance is a measure of the reliability and trustworthiness of your data analysis results. It helps you determine whether the patterns or differences you observe in your data are likely to be real or just a result of random chance.

Significance levels play a central role in hypothesis testing , a process used to make data-driven decisions. When you conduct a hypothesis test, you start with a null hypothesis (usually assuming no effect or difference) and an alternative hypothesis (proposing an effect or difference exists). The significance level you choose (commonly denoted as α) sets the threshold for rejecting the null hypothesis.

For example, if you set a significance level of 0.05 (5%), you're essentially saying, "I'm willing to accept a 5% chance of rejecting the null hypothesis when it's actually true." This means that if your p-value (the probability of observing results as extreme as yours, assuming the null hypothesis is true) is less than 0.05, you can confidently reject the null hypothesis and conclude that your results are statistically significant.

However, it's crucial to understand that p-values are often misinterpreted . A common misconception is that a p-value tells you the probability that your null hypothesis is true. In reality, it only tells you the probability of observing results as extreme as yours if the null hypothesis were true.

Another misinterpretation is that a smaller p-value always implies a larger effect size or practical importance. While a small p-value suggests that your results are unlikely to be due to chance, it doesn't necessarily mean that the effect is large or practically meaningful.

To find the appropriate significance level for your analysis, consider factors such as:

The consequences of making a Type I error (false positive) or Type II error (false negative)

The sample size and expected effect size

The conventions in your field of study

By carefully selecting your significance level and interpreting your p-values correctly, you can make sound decisions based on your data analysis results. Remember, statistical significance is just one piece of the puzzle – always consider the practical implications and context of your findings to make truly meaningful conclusions.

Why significance levels matter

Significance levels are crucial for distinguishing meaningful patterns from random noise in data. They help businesses avoid making decisions based on chance fluctuations. Setting the right significance level ensures that resources are allocated to genuine insights.

Significance levels impact business decisions and resource allocation . A stringent significance level (e.g., 0.01) reduces false positives but may miss valuable insights. A relaxed level (e.g., 0.10) captures more potential effects but risks acting on false positives. Choosing the appropriate level depends on the cost of false positives versus false negatives for your business.

Balancing statistical significance with practical relevance is key in real-world applications . A statistically significant result may not have a meaningful impact on user experience or revenue. When deciding how to find significance level, consider the practical implications alongside the statistical evidence . Focus on changes that drive tangible improvements for your users and business.

Calculating statistical significance

Formulating hypotheses is the first step in calculating statistical significance . Start by defining a null hypothesis (no significant difference) and an alternative hypothesis (presence of a meaningful difference). Choose a significance level , typically 0.01 or 0.05, which represents the probability of rejecting the null hypothesis when it's true.

Statistical tests help determine if observed differences are statistically significant. T-tests compare means between two groups, while chi-square tests analyze categorical data. ANOVA (Analysis of Variance) compares means among three or more groups. The choice of test depends on your data type and experimental design .

P-values indicate the probability of obtaining observed results if the null hypothesis is true. Compare the p-value to your chosen significance level to determine statistical significance. If the p-value is less than or equal to the significance level, reject the null hypothesis and conclude that the results are statistically significant.

To find significance level, consider the consequences of a Type I error (false positive) and a Type II error (false negative). A lower significance level reduces the risk of a Type I error but increases the risk of a Type II error. Balance these risks based on the context and implications of your study.

Sample size plays a crucial role in determining statistical significance. Larger sample sizes increase the power of a statistical test, making it easier to detect significant differences. However, an excessively large sample size can make even minor differences statistically significant, so consider practical relevance alongside statistical significance .

Effect size measures the magnitude of a difference or relationship. It provides context for interpreting statistically significant results. A small p-value doesn't always imply a large effect size, so consider both when drawing conclusions and making decisions based on your analysis .

Common pitfalls in significance testing

Overlooking sample size can lead to false conclusions. Smaller samples have less power to detect real differences, while larger samples may flag trivial differences as significant.

Misinterpreting p-values is another common mistake. A low p-value indicates strong evidence against the null hypothesis but doesn't measure the size or importance of an effect.

External factors like seasonality, marketing campaigns, or technical issues can influence results. Failing to account for these variables can skew your analysis and lead to incorrect conclusions.

To find significance level accurately:

Clearly define your null and alternative hypotheses upfront. This helps frame your analysis and interpretation of results.

Choose an appropriate significance level (usually 0.05 or 0.01) before collecting data. Stick to this predetermined level to avoid "p-hacking" or manipulating data to achieve significance.

Use the right statistical test for your data and research question. Different tests have different assumptions and are suited for various types of data.

Interpret results in context, considering both statistical significance and practical importance. A statistically significant result may not be meaningful if the effect size is small.

Replicate findings with new data when possible. Consistent results across multiple studies strengthen evidence for a genuine effect.

By understanding these pitfalls and best practices for finding significance level, you can make more reliable inferences from your data .

Practical applications of significance testing

Significance testing is a powerful tool for making data-driven decisions across various industries. By leveraging significance levels, product teams can optimize user experiences and drive meaningful improvements. Here's how you can apply significance testing in practice:

Using significance levels in product development

Identify high-impact features : Conduct A/B tests to determine which product features significantly improve user engagement or satisfaction. Focus development efforts on features that demonstrate statistically significant improvements.

Optimize user flows : Test different user flow variations to find the most intuitive and efficient paths. Use significance levels to validate that the chosen flow outperforms alternatives.

Refine UI/UX elements : Experiment with various UI/UX elements, such as button placement, color schemes, or typography. Analyze results using significance testing to select the most effective designs.

Applying statistical significance to marketing campaigns

Evaluate ad effectiveness : Compare the performance of different ad creatives, targeting strategies, or platforms. Use significance testing to identify the most impactful approaches and allocate marketing budgets accordingly.

Optimize landing pages : Test different landing page variations to maximize conversion rates. Determine the significance level of each variation's performance to implement the most effective design.

Refine email campaigns : Experiment with subject lines, email content, and call-to-actions. Use significance testing to identify the elements that drive the highest open and click-through rates.

Leveraging significance testing for data-driven decision making

Validate business strategies : Test different pricing models, product bundles, or promotional offers. Use significance levels to determine which strategies yield the best results and align with business objectives.

Improve customer support : Experiment with various support channels, response times, or communication styles. Analyze the significance of each approach's impact on customer satisfaction and loyalty.

Optimize resource allocation : Test different resource allocation strategies across departments or projects. Use significance testing to identify the most efficient and effective approaches for maximizing ROI.

By embracing significance testing as a core part of their decision-making process, organizations can confidently optimize their products , marketing efforts, and overall strategies. Significance levels provide a clear framework for determining which ideas and approaches are worth pursuing, enabling teams to focus on the most impactful initiatives.

To find significance levels, start by defining clear hypotheses and selecting appropriate statistical tests . Collect data through well-designed experiments and analyze the results using the chosen tests. Compare the p-values obtained against the predetermined significance level (e.g., 0.05) to determine if the observed differences are statistically significant.

Remember, while significance testing is a valuable tool, it should be used in conjunction with other factors, such as practical significance, user feedback, and business goals . By combining statistical insights with a holistic understanding of your users and industry, you can make informed decisions that drive meaningful growth and success.

2M Events per Month, Free Forever.

Build fast?

Try statsig today.

Top 8 common experimentation mistakes and how to fix them

I discussed 8 A/B testing mistakes with Allon Korem (Bell Statistics) and Tyler VanHaren (Statsig). Learn fixes to improve accuracy and drive better business outcomes.

Introducing Differential Impact Detection

Introducing Differential Impact Detection: Identify how different user groups respond to treatments and gain useful insights from varied experiment results.

Identifying and experimenting with Power Users using Statsig

Identify power users to drive growth and engagement. Learn to pinpoint and leverage these key players with targeted experiments for maximum impact.

How to Ingest Data Into Statsig

Simplify data pipelines with Statsig. Use SDKs, third-party integrations, and Data Warehouse Native Solution for effortless data ingestion at any stage.

A/B Testing performance wins on NestJS API servers

Learn how we use Statsig to enhance our NestJS API servers, reducing request processing time and CPU usage through performance experiments.

Skip to secondary menu
Skip to main content
Skip to primary sidebar

Statistics By Jim

Making statistics intuitive

Hypothesis Testing and Confidence Intervals

By Jim Frost 20 Comments

Confidence intervals and hypothesis testing are closely related because both methods use the same underlying methodology. Additionally, there is a close connection between significance levels and confidence levels. Indeed, there is such a strong link between them that hypothesis tests and the corresponding confidence intervals always agree about statistical significance.

A confidence interval is calculated from a sample and provides a range of values that likely contains the unknown value of a population parameter . To learn more about confidence intervals in general, how to interpret them, and how to calculate them, read my post about Understanding Confidence Intervals .

In this post, I demonstrate how confidence intervals work using graphs and concepts instead of formulas. In the process, I compare and contrast significance and confidence levels. You’ll learn how confidence intervals are similar to significance levels in hypothesis testing. You can even use confidence intervals to determine statistical significance.

Read the companion post for this one: How Hypothesis Tests Work: Significance Levels (Alpha) and P-values . In that post, I use the same graphical approach to illustrate why we need hypothesis tests, how significance levels and P-values can determine whether a result is statistically significant, and what that actually means.

Significance Level vs. Confidence Level

Let’s delve into how confidence intervals incorporate the margin of error. Like the previous post, I’ll use the same type of sampling distribution that showed us how hypothesis tests work. This sampling distribution is based on the t-distribution , our sample size , and the variability in our sample. Download the CSV data file: FuelsCosts .

There are two critical differences between the sampling distribution graphs for significance levels and confidence intervals–the value that the distribution centers on and the portion we shade.

The significance level chart centers on the null value, and we shade the outside 5% of the distribution.

Conversely, the confidence interval graph centers on the sample mean, and we shade the center 95% of the distribution.

Probability distribution plot that displays 95% confidence interval for our fuel cost dataset.

The shaded range of sample means [267 394] covers 95% of this sampling distribution. This range is the 95% confidence interval for our sample data. We can be 95% confident that the population mean for fuel costs fall between 267 and 394.

Confidence Intervals and the Inherent Uncertainty of Using Sample Data

The graph emphasizes the role of uncertainty around the point estimate . This graph centers on our sample mean. If the population mean equals our sample mean, random samples from this population (N=25) will fall within this range 95% of the time.

We don’t know whether our sample mean is near the population mean. However, we know that the sample mean is an unbiased estimate of the population mean. An unbiased estimate does not tend to be too high or too low. It’s correct on average. Confidence intervals are correct on average because they use sample estimates that are correct on average. Given what we know, the sample mean is the most likely value for the population mean.

Given the sampling distribution, it would not be unusual for other random samples drawn from the same population to have means that fall within the shaded area. In other words, given that we did, in fact, obtain the sample mean of 330.6, it would not be surprising to get other sample means within the shaded range.

If these other sample means would not be unusual, we must conclude that these other values are also plausible candidates for the population mean. There is inherent uncertainty when using sample data to make inferences about the entire population. Confidence intervals help gauge the degree of uncertainty, also known as the margin of error.

Confidence Intervals and Statistical Significance

If you want to determine whether your hypothesis test results are statistically significant, you can use either P-values with significance levels or confidence intervals. These two approaches always agree.

The relationship between the confidence level and the significance level for a hypothesis test is as follows:

Confidence level = 1 – Significance level (alpha)

For example, if your significance level is 0.05, the equivalent confidence level is 95%.

Both of the following conditions represent statistically significant results:

The P-value in a hypothesis test is smaller than the significance level.
The confidence interval excludes the null hypothesis value.

Further, it is always true that when the P-value is less than your significance level, the interval excludes the value of the null hypothesis.

In the fuel cost example, our hypothesis test results are statistically significant because the P-value (0.03112) is less than the significance level (0.05). Likewise, the 95% confidence interval [267 394] excludes the null hypotheses value (260). Using either method, we draw the same conclusion.

Hypothesis Testing and Confidence Intervals Always Agree

The hypothesis testing and confidence interval results always agree. To understand the basis of this agreement, remember how confidence levels and significance levels function:

A confidence level determines the distance between the sample mean and the confidence limits.
A significance level determines the distance between the null hypothesis value and the critical regions.

Both of these concepts specify a distance from the mean to a limit. Surprise! These distances are precisely the same length.

A 1-sample t-test calculates this distance as follows:

The critical t-value * standard error of the mean

Interpreting these statistics goes beyond the scope of this article. But, using this equation, the distance for our fuel cost example is $63.57.

P-value and significance level approach : If the sample mean is more than $63.57 from the null hypothesis mean, the sample mean falls within the critical region, and the difference is statistically significant.

Confidence interval approach : If the null hypothesis mean is more than $63.57 from the sample mean, the interval does not contain this value, and the difference is statistically significant.

Of course, they always agree!

The two approaches always agree as long as the same hypothesis test generates the P-values and confidence intervals and uses equivalent confidence levels and significance levels.

Related posts : Standard Error of the Mean and Critical Values

I Really Like Confidence Intervals!

In statistics, analysts often emphasize using hypothesis tests to determine statistical significance. Unfortunately, a statistically significant effect might not always be practically meaningful. For example, a significant effect can be too small to be important in the real world. Confidence intervals help you navigate this issue!

Similarly, the margin of error in a survey tells you how near you can expect the survey results to be to the correct population value.

Learn more about this distinction in my post about Practical vs. Statistical Significance .

Learn how to use confidence intervals to compare group means !

Finally, learn about bootstrapping in statistics to see an alternative to traditional confidence intervals that do not use probability distributions and test statistics. In that post, I create bootstrapped confidence intervals.

Neyman, J. (1937). Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability . Philosophical Transactions of the Royal Society A . 236 (767): 333–380.

Reader Interactions

December 7, 2021 at 3:14 pm

I am helping my Physics students use their data to determine whether they can say momentum is conserved. One of the columns in their data chart was change in momentum and ultimately we want this to be 0. They are obviously not getting zero from their data because of outside factors. How can I explain to them that their data supports or does not support conservation of momentum using statistics? They are using a 95% confidence level. Again, we want the change in momentum to be 0. Thank you.

December 9, 2021 at 6:54 pm

I can see several complications with that approach and also my lack of familiarity with the subject area limits what I can say. But here are some considerations.

For starters, I’m unsure whether the outside factors you mention bias the results systematically from zero or just add noise (variability) to the data (but not systematically bias).

If the outside factors bias the results to a non-zero value, then you’d expect the case where larger samples will be more likely to produce confidence intervals that exclude zero. Indeed, only smaller samples sizes might produce CIs that include zero, but that would only be due to the relative lack of precision associated with small sample sizes. In other words, limited data won’t be able to distinguish the sample value from zero even though, given the bias of the outside factors, you’d expect a non-zero value. In other words, if the bias exists, the larger samples will detect the non-zero values correctly while smaller samples might miss it.

If the outside factors don’t bias the results but just add noise, then you’d expect that both small and larger samples will include zero. However, you still have the issue of precision. Smaller samples will include zero because they’re relatively wider intervals. Larger samples should include zero but have narrower intervals. Obviously, you can trust the larger samples more.

In hypothesis testing, when you fail to reject the null, as occurs in the unbiased discussion above, you’re not accepting the null . Click the link to read about that. Failing to reject the null does not mean that the population value equals the hypothesized value (zero in your case). That’s because you can fail to reject the null due to poor quality data (high noise and/or small sample sizes). And you don’t want to draw conclusions based on poor data.

There’s a class of hypothesis testing called equivalence testing that you should use in this case. It flips the null and alternative hypotheses so that the test requires you to collect strong evidence to show that the sample value equals the null value (again, zero in your case). I don’t have a post on that topic (yet), but you can read the Wikipedia article about Equivalence Testing .

I hope that helps!

September 19, 2021 at 5:16 am

Thank you very much. When training a machine learning model using bootstrap, in the end we will have the confidence interval of accuracy. How can I say that this result is statistically significant? Do I have to convert the confidence interval to p-values first and if p-value is less than 0.05, then it is statistically significant?

September 19, 2021 at 3:16 pm

As I mention in this article, you determine significance using a confidence interval by assessing whether it excludes the null hypothesis value. When it excludes the null value, your results are statistically significant.

September 18, 2021 at 12:47 pm

Dear Jim, Thanks for this post. I am new to hypothesis testing and would like to ask you how we know that the null hypotheses value is equal to 260.

Thank you. Kind regards, Loukas

September 19, 2021 at 12:35 am

For this example, the null hypothesis is 260 because that is the value from the previous year and they wanted to compare the current year to the previous year. It’s defined as the previous year value because the goal of the study was to determine whether it has changed since last year.

In general, the null hypothesis will often be a meaningful target value for the study based on their knowledge, such as this case. In other cases, they’ll use a value that represents no effect, such as zero.

I hope that helps clarify it!

February 22, 2021 at 3:49 pm

Hello, Mr. Jim Frost.

Thank you for publishing precise information about statistics, I always read your posts and bought your excellent e-book about regression! I really learn from you.

I got a couple of questions about the confidence level of the confidence intervals. Jacob Cohen, in his article “things I’ve learned (so far)” said that, in his experience, the most useful and informative confidence level is 80%; other authors state that if that level is below 90% it would be very hard to compare across results, as it is uncommon.

My first question is: in exploratory studies, with small samples (for example, N=85), if one wishes to generate correlational hypothesis for future research, would it be better to use a lower confidence level? What is the lowest level you would consider to be acceptable? I ask that because of my own research now, and with a sample size 85 (non-probabilistic sampling) I know all I can do is generate some hypothesis to be explored in the future, so I would like my confidence intervals to be more informative, because I am not looking forward to generalize to the population.

My second question is: could you please provide an example of an appropriate way to describe the information about the confidence interval values/limits, beyond the classic “it contains a difference of 0; it contains a ratio of 1”.

I would really appreciate your answers.

Greetings from Peru!

February 23, 2021 at 4:51 pm

Thanks so much for your kind words and for supporting my regression ebook! I’m glad it’s been helpful! 🙂

On to your questions!

I haven’t read Cohen’s article, so I don’t understand his rationale. However, I’m extremely dubious of using a confidence level as low as 80%. Lowering the confidence level will create a narrower CI, which looks good. However, it comes at the expense of dramatically increasing the likelihood that the CI won’t contain the correct population value! My position is to leave the confidence level at 95%. Or, possibly lower it to 90%. But, I wouldn’t go further. Your CI will be wider, but that’s OK. It’s reflecting the uncertainty that truly exists in your data. That’s important. The problem with lowering the CIs is that it makes your results appear more precise than they actually are.

When I think of exploratory research, I think of studies that are looking at tendencies or trends. Is the overall pattern of results consistent with theoretical expectations and justify further research? At that stage, it shouldn’t be about obtaining statistically significant results–at least not as the primary objective. Additionally, exploratory research can help you derive estimated effect sizes, variability, etc. that you can use for power calculations . A smaller, exploratory study can also help you refine your methodology and not waste your resources by going straight to a larger study that, as a result, might not be as refined as it would without a test run in the smaller study. Consequently, obtaining significant results, or results that look precise when they aren’t, aren’t the top priorities.

I know that lowering the confidence level makes your CI look more information but that is deceptive! I’d resist that temptation. Maybe go down to 90%. Personally, I would not go lower.

As for the interpretation, CIs indicate the likely range that a population parameter is likely to fall within. The parameter can be a mean, effect size, ratio, etc. Often times, you as the researcher are hoping the CI excludes an important value. For example, if the CI is of the effect size, you want the CI to exclude zero (no effect). In that case, you can say that there is unlikely to be no effect in the population (i.e., there probably is a non-zero effect in the population). Additionally, the effect size is likely to be within this range. Other times, you might just want to know the range of values itself. For example, if you have a CI for the mean height of a population, it might be valuable on its own knowing that the population mean height is likely to fall between X and Y. If you have specific example of what the CI assesses, I can give you a more specific interpretation.

Additionally, I cover confidence intervals associated with many different types of hypothesis tests in my Hypothesis Testing ebook . You might consider looking in to that!

July 26, 2020 at 5:45 am

I got a very wide 95% CI of the HR of height in the cox PH model from a very large sample. I already deleted the outliers defined as 1.5 IQR, but it doesn’t work. Do you know how to resolve it?

July 5, 2020 at 6:13 pm

Hello, Jim!

I appreciate the thoughtful and thorough answer you provided. It really helped in crystallizing the topic for me.

If I may ask for a bit more of your time, as long as we are talking about CIs I have another question:

How would you go about constructing a CI for the difference of variances?

I am asking because while creating CIs for the difference of means or proportions is relatively straightforward, I couldn’t find any references for the difference of variances in any of my textbooks (or on the Web for that matter); I did find information regarding CIs for the ratio of variances, but it’s not the same thing.

Could you help me with that?

Thanks a lot!

July 2, 2020 at 6:01 pm

I want to start by thanking you for a great post and an overall great blog! Top notch material.

I have a doubt regarding the difference between confidence intervals for a point estimate and confidence intervals for a hypothesis test.

As I understand, if we are using CIs to test a hypothesis, then our point estimate would be whatever the null hypothesis is; conversely, if we are simply constructing a CI to go along with our point estimate, we’d use the point estimate derived from our sample. Am I correct so far?

The reason I am asking is that because while reading from various sources, I’ve never found a distinction between the two cases, and they seem very different to me.

Bottom line, what I am trying to ask is: assuming the null hypothesis is true, shouldn’t the CI be changed?

Thank you very much for your attention!

July 3, 2020 at 4:02 pm

There’s no difference in the math behind the scenes. The real difference is that when you create a confidence interval in conjunction with a hypothesis test, the software ensures that they’re using consistent methodology. For example, the significance level and confidence level will correspond correctly (i.e., alpha = 0.05 and confidence level = 0.95). Additionally, if you perform a two-tailed test, you will obtain a two-sided CI. On the other hand, if you perform a one-tailed test, you will obtain the appropriate upper or lower bound (i.e., one-sided CIs). The software also ensures any other methodological choices you make will match between the hypothesis test and CI, which ensures the results always agree.

You can perform them separately. However, if you don’t match all the methodology options, the results can differ.

As for your question about assuming the null is true. Keep in mind that hypothesis tests create sampling distributions that center on the null hypothesis value. That’s the assumption that the null is true. However, the sampling distributions for CIs center on the sample estimate. So, yes, CIs change that detail because they don’t assume the null is correct. But that’s always true whether you perform the hypothesis test or not.

Thanks for the great questions!

December 21, 2019 at 6:31 am

Confidence interval has sample static as the most likely value ( value in the center) – and sample distribution assumes the null value to be the most likely value( value in the center). I am a little confused about this. Would be really kind of you if you could show both in the same graph and explain how both are related. How the the distance from the mean to a limit in case of Significance level and CI same?

December 23, 2019 at 3:46 am

That’s a great question. I think part of your confusion is due to terminology.

The sampling distribution of the means centers on the sample mean. This sampling distribution uses your sample mean as its mean and the standard error of the mean as its standard deviation.

The sampling distribution of the test statistic (t) centers on the null hypothesis value (0). This distribution uses zero as its mean and also uses the SEM for its standard deviation.

They’re two different things and center on different points. But, they both incorporate the SEM, which is why they always agree! I do have section in this post about why that distance is always the same. Look for the section titled, “Why They Always Agree.”

November 23, 2019 at 11:31 pm

Hi Jim, I’m the proud owner of 2 of your ebooks. There’s one topic though that keeps puzzling me: If I would take 9 samples of size 15 in order to estimate the population mean, the se of the mean would be substantial larger than if I would take 1 sample of size 135 (divide pop sd by sqrt(15) or sqrt(135) ) whereas the E(x) (or mean of means) would be the same.

Can you please shine a little light on that.

Tx in advance

November 24, 2019 at 3:17 am

Thanks so much for supporting my ebooks. I really appreciate that!! 🙂

So, let’s flip that scenario around. If you know that a single large sample of 135 will produce more precise estimates of the population, why would you collect nine smaller samples? Knowing how statistics works, that’s not a good decision. If you did that in the real world, it would be because there was some practical reason that you could not collect one big example. Further, it would suggest that you had some reason for not being able to combine them later. For example, if you follow the same random sampling procedure on the same population and used all the same methodology and at the same general time, you might feel comfortable combining them together into one larger sample. So, if you couldn’t collect one larger example and you didn’t feel comfortable combining them together, it suggests that you have some reason for doubting that they all measure the same thing for the same population. Maybe you had differences in methodology? Or subjective measurements across different personnel? Or, maybe you collected the samples at different times and you’re worried that the population changed over time?

So, that’s the real world reason for why a researcher would not combine smaller samples into a larger one.

As you can see, the expected value for the population standard deviation is in the numerator (sigma). As the sample size increases, the numerator remains constant (plus or minus random error) because the expected value for the population parameter does not change. Conversely, the square root of the sample size is in the denominator. As the sample size increases, it produces a larger values in the denominator. So, if the expected value of the numerator is constant but the value of the denominator increases with a larger sample size, you expect the SEM to decrease. Smaller SEM’s indicate more precise estimates of the population parameter. For instance, the equations for confidence intervals use the SEM. Hence, for the same population, larger samples tend to produce smaller SEMS, and more precise estimates of the population parameter.

I hope that answers your question!

November 6, 2018 at 10:26 am

first of all: Thanks for your effort and your effective way of explaining!

You say that p-values and C.I.s always agree. I agree.

Why does Tim van der Zee claim the opposite? I’m not enough into statistcs to figure this out.

http://www.timvanderzee.com/not-interpret-confidence-intervals/

Best regards Georg

November 7, 2018 at 9:31 am

I think he is saying that they do agree–just that people often compare the wrong pair of CIs and p-values. I assume you’re referring to the section “What do overlapping intervals (not) mean?” And, he’s correct in what he says. In a 2-sample t-test, it’s not valid to compare the CI for each of the two group means to the test’s p-values because they have different purposes. Consequently, they won’t necessarily agree. However, that’s because you’re comparing results from two different tests/intervals.

On the one hand, you have the CIs for each group. On the other hand, you have the p-value for the difference between the two groups. Those are not the same thing and so it’s not surprising that they won’t agree necessarily.

However, if you compare the p-value of the difference between means to a CI of the difference between means, they will always agree. You have to compare apples to apples!

April 14, 2018 at 8:54 pm

First of all, I love all your posts and you really do make people appreciate statistics by explaining it intuitively compared to theoretical approaches I’ve come across in university courses and other online resources. Please continue the fantastic work!!!

At the end, you mentioned how you prefer confidence intervals as they consider both “size and precision of the estimated effect”. I’m confused as to what exactly size and precision mean in this context. I’d appreciate an explanation with reference to specific numbers from the example above.

Second, do p-values lack both size and precision in determination of statistical significance?

Thanks, Devansh

April 17, 2018 at 11:41 am

Hi Devansh,

Thanks for the nice comments. I really appreciate them!

I really need to write a post specifically about this issue.

Let’s first assume that we conduct our study and find that the mean cost is 330.6 and that we are testing whether that is different than 260. Further suppose that we perform the the hypothesis test and obtain a p-value that is statistically significant. We can reject the null and conclude that population mean does not equal 260. And we can see our sample estimate is 330.6. So, that’s what we learn using p-values and the sample estimate.

Confidence intervals add to that information. We know that if we were to perform the experiment again, we’d get different results. How different? Is the true population mean likely to be close to 330.6 or further away? CIs help us answer these questions. The 95% CI is [267 394]. The true population value is likely to be within this range. That range spans 127 dollars.

However, let’s suppose we perform the experiment again but this time use a much larger sample size and obtain a mean of 351 and again a significant p-value. However, thanks to the large sample size, we obtain a 95 CI of [340 362]. Now we know that the population value is likely to fall within this much tighter interval of only 22 dollars. This estimate is much more precise.

Sometimes you can obtain a significant p-value for a result that is too imprecise to be useful. For example, with first CI, it might be too wide to be useful for what we need to do with our results. Maybe we’re helping people make budgets and that is too wide to allow for practical planning. However, the more precise estimate of the second study allows for better budgetary planning! That determination how much precision is required must be made using subject-area knowledge and focusing on the practical usage of the results. P-values don’t indicate the precision of the estimates in this manner!

I hope this helps clarify this precision issue!

Comments and Questions Cancel reply

P-Value And Statistical Significance: What It Is & Why It Matters

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

The p-value in statistics quantifies the evidence against a null hypothesis. A low p-value suggests data is inconsistent with the null, potentially favoring an alternative hypothesis. Common significance thresholds are 0.05 or 0.01.

P-Value Explained in Normal Distribution

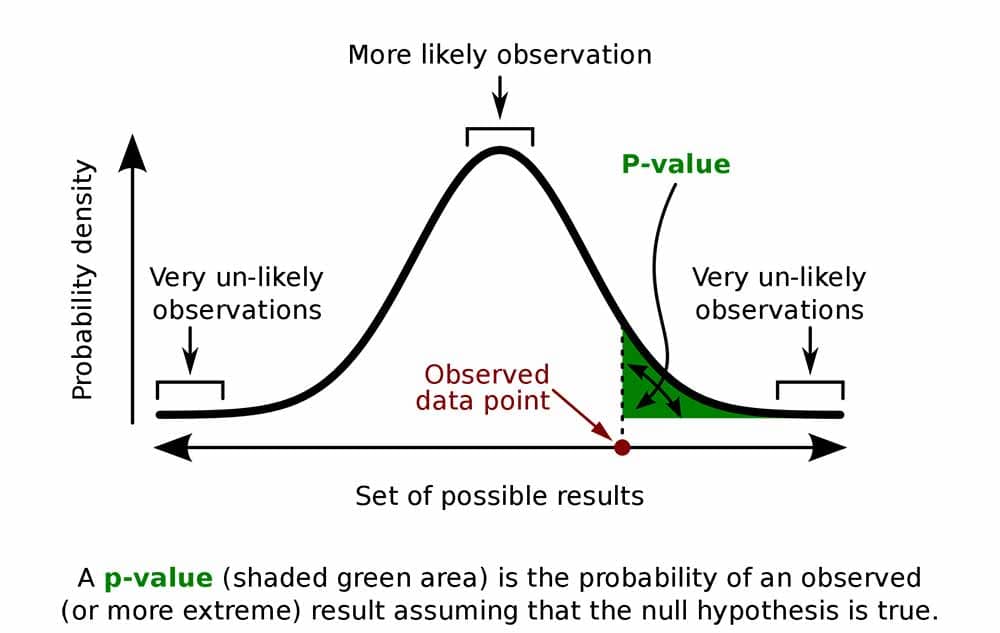
Hypothesis testing

When you perform a statistical test, a p-value helps you determine the significance of your results in relation to the null hypothesis.

The null hypothesis (H0) states no relationship exists between the two variables being studied (one variable does not affect the other). It states the results are due to chance and are not significant in supporting the idea being investigated. Thus, the null hypothesis assumes that whatever you try to prove did not happen.

The alternative hypothesis (Ha or H1) is the one you would believe if the null hypothesis is concluded to be untrue.

The alternative hypothesis states that the independent variable affected the dependent variable, and the results are significant in supporting the theory being investigated (i.e., the results are not due to random chance).

What a p-value tells you

A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true).

The level of statistical significance is often expressed as a p-value between 0 and 1.

The smaller the p -value, the less likely the results occurred by random chance, and the stronger the evidence that you should reject the null hypothesis.

Remember, a p-value doesn’t tell you if the null hypothesis is true or false. It just tells you how likely you’d see the data you observed (or more extreme data) if the null hypothesis was true. It’s a piece of evidence, not a definitive proof.

Example: Test Statistic and p-Value

Suppose you’re conducting a study to determine whether a new drug has an effect on pain relief compared to a placebo. If the new drug has no impact, your test statistic will be close to the one predicted by the null hypothesis (no difference between the drug and placebo groups), and the resulting p-value will be close to 1. It may not be precisely 1 because real-world variations may exist. Conversely, if the new drug indeed reduces pain significantly, your test statistic will diverge further from what’s expected under the null hypothesis, and the p-value will decrease. The p-value will never reach zero because there’s always a slim possibility, though highly improbable, that the observed results occurred by random chance.

P-value interpretation

The significance level (alpha) is a set probability threshold (often 0.05), while the p-value is the probability you calculate based on your study or analysis.

A p-value less than or equal to your significance level (typically ≤ 0.05) is statistically significant.

A p-value less than or equal to a predetermined significance level (often 0.05 or 0.01) indicates a statistically significant result, meaning the observed data provide strong evidence against the null hypothesis.

This suggests the effect under study likely represents a real relationship rather than just random chance.

For instance, if you set α = 0.05, you would reject the null hypothesis if your p -value ≤ 0.05.

It indicates strong evidence against the null hypothesis, as there is less than a 5% probability the null is correct (and the results are random).

Therefore, we reject the null hypothesis and accept the alternative hypothesis.

Example: Statistical Significance

Upon analyzing the pain relief effects of the new drug compared to the placebo, the computed p-value is less than 0.01, which falls well below the predetermined alpha value of 0.05. Consequently, you conclude that there is a statistically significant difference in pain relief between the new drug and the placebo.

What does a p-value of 0.001 mean?

A p-value of 0.001 is highly statistically significant beyond the commonly used 0.05 threshold. It indicates strong evidence of a real effect or difference, rather than just random variation.

Specifically, a p-value of 0.001 means there is only a 0.1% chance of obtaining a result at least as extreme as the one observed, assuming the null hypothesis is correct.

Such a small p-value provides strong evidence against the null hypothesis, leading to rejecting the null in favor of the alternative hypothesis.

A p-value more than the significance level (typically p > 0.05) is not statistically significant and indicates strong evidence for the null hypothesis.

This means we retain the null hypothesis and reject the alternative hypothesis. You should note that you cannot accept the null hypothesis; we can only reject it or fail to reject it.

Note : when the p-value is above your threshold of significance, it does not mean that there is a 95% probability that the alternative hypothesis is true.

One-Tailed Test

Probability and statistical significance in ab testing. Statistical significance in a b experiments

Two-Tailed Test

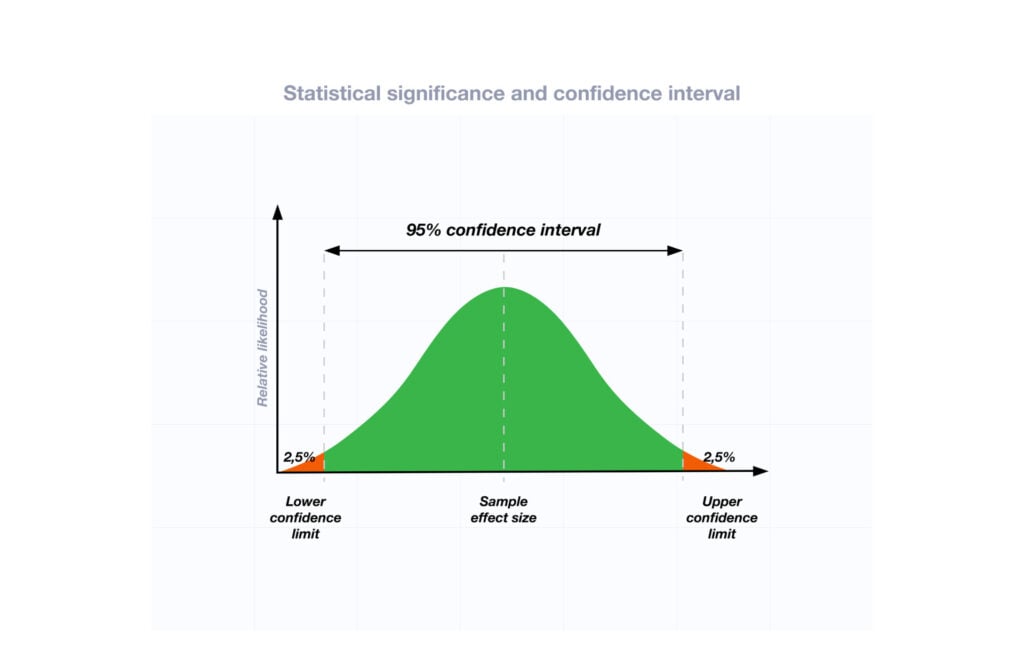
How do you calculate the p-value ?

Most statistical software packages like R, SPSS, and others automatically calculate your p-value. This is the easiest and most common way.

Online resources and tables are available to estimate the p-value based on your test statistic and degrees of freedom.

These tables help you understand how often you would expect to see your test statistic under the null hypothesis.

Understanding the Statistical Test:

Different statistical tests are designed to answer specific research questions or hypotheses. Each test has its own underlying assumptions and characteristics.

For example, you might use a t-test to compare means, a chi-squared test for categorical data, or a correlation test to measure the strength of a relationship between variables.

Be aware that the number of independent variables you include in your analysis can influence the magnitude of the test statistic needed to produce the same p-value.

This factor is particularly important to consider when comparing results across different analyses.

Example: Choosing a Statistical Test

If you’re comparing the effectiveness of just two different drugs in pain relief, a two-sample t-test is a suitable choice for comparing these two groups. However, when you’re examining the impact of three or more drugs, it’s more appropriate to employ an Analysis of Variance ( ANOVA) . Utilizing multiple pairwise comparisons in such cases can lead to artificially low p-values and an overestimation of the significance of differences between the drug groups.

How to report

A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty).

Instead, we may state our results “provide support for” or “give evidence for” our research hypothesis (as there is still a slight probability that the results occurred by chance and the null hypothesis was correct – e.g., less than 5%).

Example: Reporting the results

In our comparison of the pain relief effects of the new drug and the placebo, we observed that participants in the drug group experienced a significant reduction in pain ( M = 3.5; SD = 0.8) compared to those in the placebo group ( M = 5.2; SD = 0.7), resulting in an average difference of 1.7 points on the pain scale (t(98) = -9.36; p < 0.001).

The 6th edition of the APA style manual (American Psychological Association, 2010) states the following on the topic of reporting p-values:

“When reporting p values, report exact p values (e.g., p = .031) to two or three decimal places. However, report p values less than .001 as p < .001.

The tradition of reporting p values in the form p < .10, p < .05, p < .01, and so forth, was appropriate in a time when only limited tables of critical values were available.” (p. 114)

Do not use 0 before the decimal point for the statistical value p as it cannot equal 1. In other words, write p = .001 instead of p = 0.001.
Please pay attention to issues of italics ( p is always italicized) and spacing (either side of the = sign).
p = .000 (as outputted by some statistical packages such as SPSS) is impossible and should be written as p < .001.
The opposite of significant is “nonsignificant,” not “insignificant.”

Why is the p -value not enough?

A lower p-value is sometimes interpreted as meaning there is a stronger relationship between two variables.

However, statistical significance means that it is unlikely that the null hypothesis is true (less than 5%).

To understand the strength of the difference between the two groups (control vs. experimental) a researcher needs to calculate the effect size .

When do you reject the null hypothesis?

In statistical hypothesis testing, you reject the null hypothesis when the p-value is less than or equal to the significance level (α) you set before conducting your test. The significance level is the probability of rejecting the null hypothesis when it is true. Commonly used significance levels are 0.01, 0.05, and 0.10.

Remember, rejecting the null hypothesis doesn’t prove the alternative hypothesis; it just suggests that the alternative hypothesis may be plausible given the observed data.

The p -value is conditional upon the null hypothesis being true but is unrelated to the truth or falsity of the alternative hypothesis.

What does p-value of 0.05 mean?

If your p-value is less than or equal to 0.05 (the significance level), you would conclude that your result is statistically significant. This means the evidence is strong enough to reject the null hypothesis in favor of the alternative hypothesis.

Are all p-values below 0.05 considered statistically significant?

No, not all p-values below 0.05 are considered statistically significant. The threshold of 0.05 is commonly used, but it’s just a convention. Statistical significance depends on factors like the study design, sample size, and the magnitude of the observed effect.

A p-value below 0.05 means there is evidence against the null hypothesis, suggesting a real effect. However, it’s essential to consider the context and other factors when interpreting results.

Researchers also look at effect size and confidence intervals to determine the practical significance and reliability of findings.

How does sample size affect the interpretation of p-values?

Sample size can impact the interpretation of p-values. A larger sample size provides more reliable and precise estimates of the population, leading to narrower confidence intervals.

With a larger sample, even small differences between groups or effects can become statistically significant, yielding lower p-values. In contrast, smaller sample sizes may not have enough statistical power to detect smaller effects, resulting in higher p-values.

Therefore, a larger sample size increases the chances of finding statistically significant results when there is a genuine effect, making the findings more trustworthy and robust.

Can a non-significant p-value indicate that there is no effect or difference in the data?

No, a non-significant p-value does not necessarily indicate that there is no effect or difference in the data. It means that the observed data do not provide strong enough evidence to reject the null hypothesis.

There could still be a real effect or difference, but it might be smaller or more variable than the study was able to detect.

Other factors like sample size, study design, and measurement precision can influence the p-value. It’s important to consider the entire body of evidence and not rely solely on p-values when interpreting research findings.

Can P values be exactly zero?

While a p-value can be extremely small, it cannot technically be absolute zero. When a p-value is reported as p = 0.000, the actual p-value is too small for the software to display. This is often interpreted as strong evidence against the null hypothesis. For p values less than 0.001, report as p < .001

Further Information

P Value Calculator From T Score
P-Value Calculator For Chi-Square
P-values and significance tests (Kahn Academy)
Hypothesis testing and p-values (Kahn Academy)
Wasserstein, R. L., Schirm, A. L., & Lazar, N. A. (2019). Moving to a world beyond “ p “< 0.05”.
Criticism of using the “ p “< 0.05”.
Publication manual of the American Psychological Association
Statistics for Psychology Book Download

Bland, J. M., & Altman, D. G. (1994). One and two sided tests of significance: Authors’ reply. BMJ: British Medical Journal , 309 (6958), 874.

Goodman, S. N., & Royall, R. (1988). Evidence and scientific research. American Journal of Public Health , 78 (12), 1568-1574.

Goodman, S. (2008, July). A dirty dozen: twelve p-value misconceptions . In Seminars in hematology (Vol. 45, No. 3, pp. 135-140). WB Saunders.

Lang, J. M., Rothman, K. J., & Cann, C. I. (1998). That confounded P-value. Epidemiology (Cambridge, Mass.) , 9 (1), 7-8.

Math Article
Level Of Significance

Level of Significance

Statistics is a branch of Mathematics. It deals with gathering, presenting, analyzing, organizing and interpreting the data, which is usually numerical. It is applied to many industrial, scientific, social and economic areas. While a researcher performs research, a hypothesis has to be set, which is known as the null hypothesis . This hypothesis is required to be tested via pre-defined statistical examinations. This process is termed as statistical hypothesis testing. The level of significance or Statistical significance is an important terminology that is quite commonly used in Statistics. In this article, we are going to discuss the level of significance in detail.

What is Statistical Significance?

In Statistics, “significance” means “not by chance” or “probably true”. We can say that if a statistician declares that some result is “highly significant”, then he indicates by stating that it might be very probably true. It does not mean that the result is highly significant, but it suggests that it is highly probable.

Level of Significance Definition

The level of significance is defined as the fixed probability of wrong elimination of null hypothesis when in fact, it is true. The level of significance is stated to be the probability of type I error and is preset by the researcher with the outcomes of error. The level of significance is the measurement of the statistical significance. It defines whether the null hypothesis is assumed to be accepted or rejected. It is expected to identify if the result is statistically significant for the null hypothesis to be false or rejected.

Level of Significance Symbol

The level of significance is denoted by the Greek symbol α (alpha). Therefore, the level of significance is defined as follows:

Significance Level = p (type I error) = α

The values or the observations are less likely when they are farther than the mean. The results are written as “significant at x%”.

Example: The value significant at 5% refers to p-value is less than 0.05 or p < 0.05. Similarly, significant at the 1% means that the p-value is less than 0.01.

The level of significance is taken at 0.05 or 5%. When the p-value is low, it means that the recognised values are significantly different from the population value that was hypothesised in the beginning. The p-value is said to be more significant if it is as low as possible. Also, the result would be highly significant if the p-value is very less. But, most generally, p-values smaller than 0.05 are known as significant, since getting a p-value less than 0.05 is quite a less practice.

How to Find the Level of Significance?

To measure the level of statistical significance of the result, the investigator first needs to calculate the p-value. It defines the probability of identifying an effect which provides that the null hypothesis is true. When the p-value is less than the level of significance (α), the null hypothesis is rejected. If the p-value so observed is not less than the significance level α, then theoretically null hypothesis is accepted. But practically, we often increase the size of the sample size and check if we reach the significance level. The general interpretation of the p-value based upon the level of significance of 10%:

If p > 0.1, then there will be no assumption for the null hypothesis
If p > 0.05 and p ≤ 0.1, it means that there will be a low assumption for the null hypothesis.
If p > 0.01 and p ≤ 0.05, then there must be a strong assumption about the null hypothesis.
If p ≤ 0.01, then a very strong assumption about the null hypothesis is indicated.

Level of Significance Example

If we obtain a p-value equal to 0.03, then it indicates that there are just 3% chances of getting a difference larger than that in our research, given that the null hypothesis exists. Now, we need to determine if this result is statistically significant enough.

We know that if the chances are 5% or less than that, then the null hypothesis is true, and we will tend to reject the null hypothesis and accept the alternative hypothesis. Here, in this case, the chances are 0.03, i.e. 3% (less than 5%), which eventually means that we will eliminate our null hypothesis and will accept an alternative hypothesis.

MATHS Related Links

Register with BYJU'S & Download Free PDFs

Hypothesis Testing for Means & Proportions

1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10

Hypothesis Testing: Upper-, Lower, and Two Tailed Tests

Type i and type ii errors.

All Modules

Z score Table

t score Table

The procedure for hypothesis testing is based on the ideas described above. Specifically, we set up competing hypotheses, select a random sample from the population of interest and compute summary statistics. We then determine whether the sample data supports the null or alternative hypotheses. The procedure can be broken down into the following five steps.

Step 1. Set up hypotheses and select the level of significance α.

H 0 : Null hypothesis (no change, no difference);

H 1 : Research hypothesis (investigator's belief); α =0.05

Upper-tailed, Lower-tailed, Two-tailed Tests

The research or alternative hypothesis can take one of three forms. An investigator might believe that the parameter has increased, decreased or changed. For example, an investigator might hypothesize:

: μ > μ , where μ is the comparator or null value (e.g., μ =191 in our example about weight in men in 2006) and an increase is hypothesized - this type of test is called an ; : μ < μ , where a decrease is hypothesized and this is called a ; or : μ ≠ μ where a difference is hypothesized and this is called a .

The exact form of the research hypothesis depends on the investigator's belief about the parameter of interest and whether it has possibly increased, decreased or is different from the null value. The research hypothesis is set up by the investigator before any data are collected.

Step 2. Select the appropriate test statistic.

The test statistic is a single number that summarizes the sample information. An example of a test statistic is the Z statistic computed as follows:

When the sample size is small, we will use t statistics (just as we did when constructing confidence intervals for small samples). As we present each scenario, alternative test statistics are provided along with conditions for their appropriate use.

Step 3. Set up decision rule.

The decision rule is a statement that tells under what circumstances to reject the null hypothesis. The decision rule is based on specific values of the test statistic (e.g., reject H 0 if Z > 1.645). The decision rule for a specific test depends on 3 factors: the research or alternative hypothesis, the test statistic and the level of significance. Each is discussed below.

The decision rule depends on whether an upper-tailed, lower-tailed, or two-tailed test is proposed. In an upper-tailed test the decision rule has investigators reject H 0 if the test statistic is larger than the critical value. In a lower-tailed test the decision rule has investigators reject H 0 if the test statistic is smaller than the critical value. In a two-tailed test the decision rule has investigators reject H 0 if the test statistic is extreme, either larger than an upper critical value or smaller than a lower critical value.
The exact form of the test statistic is also important in determining the decision rule. If the test statistic follows the standard normal distribution (Z), then the decision rule will be based on the standard normal distribution. If the test statistic follows the t distribution, then the decision rule will be based on the t distribution. The appropriate critical value will be selected from the t distribution again depending on the specific alternative hypothesis and the level of significance.
The third factor is the level of significance. The level of significance which is selected in Step 1 (e.g., α =0.05) dictates the critical value. For example, in an upper tailed Z test, if α =0.05 then the critical value is Z=1.645.

The following figures illustrate the rejection regions defined by the decision rule for upper-, lower- and two-tailed Z tests with α=0.05. Notice that the rejection regions are in the upper, lower and both tails of the curves, respectively. The decision rules are written below each figure.

Rejection Region for Upper-Tailed Z Test (H : μ > μ ) with α=0.05

The decision rule is: Reject H if Z 1.645.


α	Z
0.10	1.282
0.05	1.645
0.025	1.960
0.010	2.326
0.005	2.576
0.001	3.090
0.0001	3.719

Standard normal distribution with lower tail at -1.645 and alpha=0.05

Rejection Region for Lower-Tailed Z Test (H 1 : μ < μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < 1.645.


a	Z
0.10	-1.282
0.05	-1.645
0.025	-1.960
0.010	-2.326
0.005	-2.576
0.001	-3.090
0.0001	-3.719

Standard normal distribution with two tails

Rejection Region for Two-Tailed Z Test (H 1 : μ ≠ μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < -1.960 or if Z > 1.960.



0.20	1.282
0.10	1.645
0.05	1.960
0.010	2.576
0.001	3.291
0.0001	3.819

The complete table of critical values of Z for upper, lower and two-tailed tests can be found in the table of Z values to the right in "Other Resources."

Critical values of t for upper, lower and two-tailed tests can be found in the table of t values in "Other Resources."

Step 4. Compute the test statistic.

Here we compute the test statistic by substituting the observed sample data into the test statistic identified in Step 2.

Step 5. Conclusion.

The final conclusion is made by comparing the test statistic (which is a summary of the information observed in the sample) to the decision rule. The final conclusion will be either to reject the null hypothesis (because the sample data are very unlikely if the null hypothesis is true) or not to reject the null hypothesis (because the sample data are not very unlikely).

If the null hypothesis is rejected, then an exact significance level is computed to describe the likelihood of observing the sample data assuming that the null hypothesis is true. The exact level of significance is called the p-value and it will be less than the chosen level of significance if we reject H 0 .

Statistical computing packages provide exact p-values as part of their standard output for hypothesis tests. In fact, when using a statistical computing package, the steps outlined about can be abbreviated. The hypotheses (step 1) should always be set up in advance of any analysis and the significance criterion should also be determined (e.g., α =0.05). Statistical computing packages will produce the test statistic (usually reporting the test statistic as t) and a p-value. The investigator can then determine statistical significance using the following: If p < α then reject H 0 .

Step 1. Set up hypotheses and determine level of significance

H 0 : μ = 191 H 1 : μ > 191 α =0.05

The research hypothesis is that weights have increased, and therefore an upper tailed test is used.

Step 2. Select the appropriate test statistic.

Because the sample size is large (n > 30) the appropriate test statistic is

Step 3. Set up decision rule.

In this example, we are performing an upper tailed test (H 1 : μ> 191), with a Z test statistic and selected α =0.05. Reject H 0 if Z > 1.645.

We now substitute the sample data into the formula for the test statistic identified in Step 2.

We reject H 0 because 2.38 > 1.645. We have statistically significant evidence at a =0.05, to show that the mean weight in men in 2006 is more than 191 pounds. Because we rejected the null hypothesis, we now approximate the p-value which is the likelihood of observing the sample data if the null hypothesis is true. An alternative definition of the p-value is the smallest level of significance where we can still reject H 0 . In this example, we observed Z=2.38 and for α=0.05, the critical value was 1.645. Because 2.38 exceeded 1.645 we rejected H 0 . In our conclusion we reported a statistically significant increase in mean weight at a 5% level of significance. Using the table of critical values for upper tailed tests, we can approximate the p-value. If we select α=0.025, the critical value is 1.96, and we still reject H 0 because 2.38 > 1.960. If we select α=0.010 the critical value is 2.326, and we still reject H 0 because 2.38 > 2.326. However, if we select α=0.005, the critical value is 2.576, and we cannot reject H 0 because 2.38 < 2.576. Therefore, the smallest α where we still reject H 0 is 0.010. This is the p-value. A statistical computing package would produce a more precise p-value which would be in between 0.005 and 0.010. Here we are approximating the p-value and would report p < 0.010.

In all tests of hypothesis, there are two types of errors that can be committed. The first is called a Type I error and refers to the situation where we incorrectly reject H 0 when in fact it is true. This is also called a false positive result (as we incorrectly conclude that the research hypothesis is true when in fact it is not). When we run a test of hypothesis and decide to reject H 0 (e.g., because the test statistic exceeds the critical value in an upper tailed test) then either we make a correct decision because the research hypothesis is true or we commit a Type I error. The different conclusions are summarized in the table below. Note that we will never know whether the null hypothesis is really true or false (i.e., we will never know which row of the following table reflects reality).

Table - Conclusions in Test of Hypothesis


is True	Correct Decision	Type I Error
is False	Type II Error	Correct Decision

In the first step of the hypothesis test, we select a level of significance, α, and α= P(Type I error). Because we purposely select a small value for α, we control the probability of committing a Type I error. For example, if we select α=0.05, and our test tells us to reject H 0 , then there is a 5% probability that we commit a Type I error. Most investigators are very comfortable with this and are confident when rejecting H 0 that the research hypothesis is true (as it is the more likely scenario when we reject H 0 ).

When we run a test of hypothesis and decide not to reject H 0 (e.g., because the test statistic is below the critical value in an upper tailed test) then either we make a correct decision because the null hypothesis is true or we commit a Type II error. Beta (β) represents the probability of a Type II error and is defined as follows: β=P(Type II error) = P(Do not Reject H 0 | H 0 is false). Unfortunately, we cannot choose β to be small (e.g., 0.05) to control the probability of committing a Type II error because β depends on several factors including the sample size, α, and the research hypothesis. When we do not reject H 0 , it may be very likely that we are committing a Type II error (i.e., failing to reject H 0 when in fact it is false). Therefore, when tests are run and the null hypothesis is not rejected we often make a weak concluding statement allowing for the possibility that we might be committing a Type II error. If we do not reject H 0 , we conclude that we do not have significant evidence to show that H 1 is true. We do not conclude that H 0 is true.

The most common reason for a Type II error is a small sample size.

return to top | previous page | next page

Hypothesis Testing ( AQA A Level Maths: Statistics )

Revision note.

Language of Hypothesis Testing

What is a hypothesis test.

A hypothesis test uses a sample of data in an experiment to test a statement made about the value of a population parameter
A hypothesis test is used when the value of the assumed population parameter is questioned
The hypothesis test will look at the which outcomes are unlikely to occur if assumed population parameter is true
The probability found will be compared against a given significance level to determine whether there is evidence to believe that the assumed population parameter is not true

What are the key terms used in statistical hypothesis testing?

Every hypothesis test must begin with a clear null hypothesis (what we believe to already be true) and alternative hypothesis (how we believe the data pattern or probability distribution might have changed)
One example of a population parameter is the probability, p of an event occurring
Another example is the mean of a population
The null hypothesis is denoted H 0 and sets out the assumed population parameter given that no change has happened
The alternative hypothesis is denoted H 1 and sets out how we think the population parameter could have changed
When a hypothesis test is carried out, the null hypothesis is assumed to be true and this assumption will either be accepted or rejected
A hypothesis test could be a one-tailed test or a two-tailed test
The null hypothesis will always be H 0 : θ = ...
The alternative hypothesis, H 1 will be H 1 : θ > ... or H 1 : θ < ...
The alternative hypothesis, H 1 will be H 1 : θ ≠ ...
It is important to read the wording of the question carefully to decide whether your hypothesis test should be one-tailed or two-tailed
A sample of data is a subset of data taken from the population
The test statistic is a numerical value calculated from the of data
Any probability smaller than the significance level would suggest that the event is unlikely to have happened by chance
The significance level must be set before the hypothesis test is carried out
The significance level will usually be 1%, 5% or 10%, however it may vary

Worked example

A hypothesis test is carried out at the 5% level of significance to test if a normal coin is fair or not.

5-1-1-language-of-hypothesis-testing-we-solution

Make sure you read the question carefully to determine whether the test you are carrying out is for a one-tailed or a two-tailed test and use the level of significance accordingly.

Critical Regions & p-values

How do we decide whether to reject or accept the null hypothesis.

If the test is looking for a decrease then extreme values are smaller than the test statistic, so find the probability of less than or equal to the test statistic
If the test is looking for an increase then extreme values are bigger than the test statistic, so find the probability of greater than or equal to the test statistic
Though for a two-tailed test it is common to half the significance level and compare this with the probability (rather than doubling the probability)
If the test statistic falls within the critical region, the null hypothesis would be rejected
It is the least extreme value that would lead to the rejection of the null hypothesis
The critical value is determined by the significance level
In a two-tailed test the significance level is halved and both the upper and the lower tails are tested
This probability will be known as the actual significance level
The actual significance level is the probability of incorrectly rejecting the null hypothesis
Finding the critical region will be different for a two-tailed test than it is for a one-tailed test

For the following situations, state at the 1% and 5% significance levels whether the null hypothesis should be rejected or not.

5-1-1-critical-regions-and-p-values-we-solution

Conclusions of Hypothesis Testing

How is a hypothesis test carried out.

There are a number of ways that a hypothesis test can be carried out for different models, however the following steps should form the base for your test:
Step 1. Define the test statistic and population parameter
Step 2. Write the null and alternative hypotheses clearly
Step 3. Calculate the critical value(s) or the p - value for the test
Step 4. Compare the observed value of the test statistic with the critical value(s) or the p - value with the significance level
Step 5. Decide whether there is enough evidence to reject H 0 or whether it has to be accepted
Step 6. Write a conclusion in context

How should a conclusion be written for a hypothesis test?

Your conclusion must be written in the context of the question
If rejecting the null hypothesis your conclusion should state that there is sufficient evidence to suggest the alternative hypothesis is true at this level of significance
If accepting the null hypothesis your conclusion should state that there is not enough evidence to suggest the alternative hypothesis is true at this level of significance
There is a chance that the test has led to an incorrect conclusion
The outcome is dependent on the sample, a different sample might lead to a different outcome
You should not state whether this change is an increase or decrease

A teacher carried out a hypothesis test at the 10% significance level to test if her students perform better in exams after using a new revision technique. The p – value for her test statistic is 0.09142. Write a conclusion for her hypothesis test.

5-1-1-conclusions-of-hypothesis-testing-we-solution

It is best to use the exact wording from the question when writing your conclusion for the hypothesis test, do not be afraid to sound repetitive.

You've read 0 of your 0 free revision notes

Get unlimited access.

to absolutely everything:

Downloadable PDFs
Unlimited Revision Notes
Topic Questions
Past Papers
Model Answers
Videos (Maths and Science)

Join the 100,000 + Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Did this page help you?

Author: Amber

Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Statistics and probability

Course: statistics and probability > unit 12, hypothesis testing and p-values.

One-tailed and two-tailed tests
Z-statistics vs. T-statistics
Small sample hypothesis test
Large sample proportion hypothesis testing

Want to join the conversation?

Upvote Button navigates to signup page
Downvote Button navigates to signup page
Flag Button navigates to signup page

Video transcript

School Guide
Mathematics
Number System and Arithmetic
Trigonometry
Probability
Mensuration
Maths Formulas
Class 8 Maths Notes
Class 9 Maths Notes
Class 10 Maths Notes
Class 11 Maths Notes
Class 12 Maths Notes

Tests of Significance: Process, Example and Type

Test of significance is a process for comparing observed data with a claim(also called a hypothesis), the truth of which is being assessed in further analysis. Let’s learn about test of significance, null hypothesis and Significance testing below.

Tests of Significance in Statistics

In technical terms, it is a probability measurement of a certain statistical test or research in the theory making in a way that the outcome must have occurred by chance instead of the test or experiment being right. The ultimate goal of descriptive statistical research is the revelation of the truth In doing so, the researcher has to make sure that the sample is of good quality, the error is minimal, and the measures are precise. These things are to be completed through several stages. The researcher will need to know whether the experimental outcomes are from a proper study process or just due to chance.

The sample size is the one that primarily specifies the probability that the event could occur without the effect of really performed research. It may be weak or strong depending on a certain statistical significance. Its bearings are put into question. They may or may not make a difference. The presence of a careless researcher can be a start of when a researcher instead of carefully making use of language in the report of his experiment, the significance of the study might be misinterpreted.

Significance Testing

Statistics involves the issue of assessing whether a result obtained from an experiment is important enough or not. In the field of quantitative significance, there are defined tests that may have relevant uses. The designation of tests depends on the type of tests or the tests of significance are more known as the simple significance tests.

These stand up for certain levels of error mislead. Sometimes the trial designer is called upon to predefine the probability of sampling error in the initial stage of the experiment. The population sampling test is regarded as one which does not study the whole, and as such the sampling error always exists. The testing of the significance is an equally important part of the statistical research.

Null Hypothesis

Every test for significance starts with a null hypothesis H 0 . H 0 represents a theory that has been suggested, either because it’s believed to be true or because it’s to be used as a basis for argument, but has not been proved. For example, during a clinical test of a replacement drug, the null hypothesis could be that the new drug is not any better, on average than the present drug. We would write H 0 : there’s no difference between the 2 drugs on average.

Process of Significance Testing

In the process of testing for statistical significance, the following steps must be taken:

Step 1: Start by coming up with a research idea or question for your thesis. Step 2: Create a neutral comparison to test against your hypothesis. Step 3: Decide on the level of certainty you need for your results, which affects the type of sign language translators and communication methods you’ll use. Step 4: Choose the appropriate statistical test to analyze your data accurately. Step 5: Understand and explain what your results mean in the context of your research question.

Types of Errors

There are basically two types of errors:

Type I Error

Type ii error.

Now let’s learn about these errors in detail.

A type I error is where the researcher finds out that the relationship presumed maxim is a case; however, there is evidence showing it is not a function explained. This type of error leads to a failure of the researcher who says that the H 0 or null hypothesis has to be accepted while in reality, it was supposed to be rejected together with the research hypothesis. Researchers commit an error in the first type when α (alpha) is their probability.

Type II error is the same as the type I error is the case. You begin to suppress your emotions and avoid experiencing any connection when someone thinks that you have no relation even though there does exist among you. In this sort of error, the researcher is expected to see the research hypothesis as true and treat the null hypotheses as false while he may do not and the opposite situation happens. Type II error is identified with β that equals to the possibility to make a type II error which is an error of omission.

Statistical Tests

One-tailed and two-tailed statistical tests help determine how significant a finding is in a set of data.

When we think that a parameter might change in one specific direction from a baseline, we use a one-tailed test. For example, if we’re testing whether a new drug makes people perform better, we might only care if it improves performance, not if it makes it worse.

On the flip side, a two-tailed test comes into play when changes could go in either direction from the baseline. For instance, if we’re studying the effect of a new teaching method on test scores, we’d want to know if it makes scores better or worse, so we’d use a two-tailed test.

Types of Statistical Tests

Hypothesis testing can be done via use of either one-tailed or two-tailed statistical test. The purpose of these tests is to obtain the probability with which a parameter from a given data set is statistically significant. These are also called lateral flow and dipstick tests.

One-tailed test can be used so that the differences of the parameter estimations within only one side from a given standard can be perceived plausible.
Two-tailed test needs to be applied in the case when you consider deviations from both sides of benchmark value as possible in science.

The expression “tail” is used in the terminology in which those tests are referred and the reason for that is that outliers, i.e. observation ended up rejecting the null hypothesis, are the extreme points of the distribution, those areas normally have a small influence or “tail off” similar to the bell shape or normal distribution. One study should make an application either the one-tailed test or two-tailed test according to the judgment of the research hypothesis.

What is p-Value Testing?

In the case of data information significance, the p-value is an additional and significant term for hypothesis testing. The p-value is a function whose domain is the observed result of sample and range is testing subset of statistical hypothesis which is being used for testing of statistical hypothesis. It must determine what the threshold value is before starting of the test. The significance level holds the name, traditional 1% or 5%, which stands for the level of the significance considered to be of value. One of the parameters of the Savings function is α.

In the condition if the p-value is greater than or equal the α term, inconsistency between our null model and the data exists. As a result the null hypothesis should be rejected and a new hypothesis may be supposed being true, or may be assumed as such one.

Example on Test of Significance

Some examples of test of significance are added below:

Example 1: T-Test for Medical Research – The T Test

For example, a medical study researching the performance of a new drug that comes to the conclusion of a reduced in blood pressure. The researchers predict that the patients taking the new drug will show a frankly larger decrease in blood pressure as opposed to the study participants on a placebo. They collect data from two groups: treat one group with an experimental drug and give all the placebo to the second group.

Researchers apply a t-test to the data in order determine the value of two assumed normal populations difference and study whether it statistically significant. The H0 (null hypothesis) could state that there is no significant difference in the blood pressure registered in the two groups of subjects, while the HA1 (alternative hypothesis) should be indicating the positivity of a significant difference. They can check whether or not the outcomes are significantly different by using the t-test, and therefore reduce the possibility of any confusing hypotheses.

Example 2: Chi-Square Analysis in Market Research

Think about the situation where you have to carry out a market research work to ascertain the link between customers satisfaction (comprised of satisfied satisfied or neutral scores) and their product preferences (the three products designated as Product A, Product B, and Product C). A chi-square test was used by the researchers to check whether they had a substantial association with the two categorical variables they were dealing with.

The H0 null hypothesis states customer satisfaction and product preferences are unrelated, the contrary to which H1 alternative hypothesis shows the customers’ satisfaction and product preferences are related. Thereby, the researchers will be able to execute the chi-square test on the gathered data and find out if the existed observations among customer satisfaction and product preferences are statistically significant by doing so. This allows us to make conclusions how the satisfaction degree of customers affects the market conception of goods for the target market.

Example 3: ANOVA in Educational Research

Think of a researcher whom is studying if there is any difference between various learning ways and their effect on students’ study achievements. HO represents the null hypothesis which asserts no differences in scores for the groups while the alternative hypothesis (HA) claims at least one group has a different mean. Via use Analysis of Variance ( ANOVA ), a researcher determines whether or not there is any statistically significant difference in performance hence, across the methods of teaching.

Example 4: Regression Analysis in Economics

In an economic study, researchers examine the connection between ads cost and revenue for the group of businesses that have recently disclosed their financial results. The null space proposes that there is no such linear connection between the advertisement spending and purchases.

Among the models, the regression analysis used to determine whether the changes in sales are attributed to the changes in advertising to a statistically significant level (the regression line slope is significantly different from zero) is chosen.

Example 5: Paired T-Test in Psychology

A psychologist decides to do a study to find out if a new type of therapy can make someone get rid of anxiety. Patients are evaluated of their level of anxiety prior to initiating the intervention and right after.

The null hypothesis claims that there is no noticeable difference in the levels of anxiety from a pre-intervention to a post-intervention setting. Using a paired t-test, a psychologist who collected the anxiety scores of a group before and after the experiment can prove statistically the observed change in these scores.

Must Check

Test of Significance – FAQs

What is test of significance.

Test of significance is a process for comparing observed data with a claim(also called a hypothesis), the truth of which is being assessed in further analysis.

Define Statistical Significance Test?

Random distribution of observed data implies that there must be a certain cause behind which could then be associated with the data. This outcome is also referred to as the statistical significance. Whatever the explicit field or the profession that rely utterly on numbers and research, like finance, economics, investing, medicine, and biology, statistic is important.

What is the meaning of a test of significance?

Statistical significant tests work in order to determine if the differences found in assessment data is just due to random errors arising from sampling or not. This is a “silent” category of research that ought to be overlooked for it brings on mere incompatibilities.

What is the importance of the Significance test?

In experiments, the significance tests indeed have specific applied value. That is because they help researchers to draw conclusion whether the data supports or not the null hypothesis, and therefore whether the alternative hypothesis is true or not.

How many types of Significance tests are there in statistical mathematics?

In statistics, we have tests like t-test, aZ-test, chi-square test, annoVA test, binomial test, mediana test and others. Greatly decentralized data can be tested with parametric tests.

How does choosing a significance level (α) influence the interpretation of the attributable tests?

The parameter α which stands for the significance level is a function of this threshold, and to fail this test null hypothesis value has to be rejected. Hence, a smaller α value means higher strictness of acceptance threshold and false positives are limited while there could be an increase in false negatives.

Is significance testing limited to parametric methods like comparison of two means or, it can be applied to non-parametric datasets also?

Inference is something useful which can be miscellaneous and can adapt to parametric or non-parametric data. Non-parametric tests, for instance the Mann-Whitney U test and the Wilcoxon signed-rank test, are often applied in operations research, since they do not require that data meet the assumptions of parametric tests.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

if the cost of a type i error is high, a smaller value should be chosen for the . a. level of significance b. confidence coefficient c. test statistic d. critical value

A lower degree of significance should be selected if the cost of a Type I error is substantial.

The level of significance chosen for the hypothesis test is equivalent to the likelihood of making a type I error. Therefore, there is a 5% probability that a type I mistake could happen if the threshold of significance is 0.05.

Two things can lead to type 1 errors : poor research methods and random chance. No random sample, whether it be an A/B test or a pre-election survey, can ever accurately represent the population it is meant to characterize.

To know more about Type 1 errors , visit,

https://brainly.com/question/29854786

Related Questions

Determine whether the sequence converges or diverges. If itconverge, find the limit. an = ln( 2n^2 + 1 ) - ln( n^2 +1 )

The sequence converges to 2 .

To determine the convergence or divergence of the sequence , we need to take the limit of the sequence as n approaches infinity.

Let's begin by simplifying the expression for an:

an = ln(2n^2 + 1) - ln(n^2 + 1)

= ln[(2n^2 + 1)/(n^2 + 1)]

Now, taking the limit of this expression as n approaches infinity , we get:

lim(n→∞) [(2n^2 + 1)/(n^2 + 1)]

Using the fact that the limit of a ratio of two polynomials with equal degree is equal to the ratio of their leading coefficients, we can simplify the expression as follows:

= lim(n→∞) [(2 + 1/n^2)/(1 + 1/n^2)]

Therefore, the sequence converges to 2.

Learn more about sequence

brainly.com/question/21961097

Refer to the vectors m through t at the right Name all groups of vectors that appear to be equal Choose the correct answer below OA, mand p, n and r OB, m,o' p and qin, r, and s O C. n and r, m, p, and t O D. m and p: p and q; m and q n and r; n and s; s and r Click to select your answer Save for Later /171717-17171717-1/1/1/1/17:ハハハハハハハハハハハハハハー米 19 8 5 6

Vectors that appear to be equal is OB, m, o', p and qin, r, and s.

Let's discuss it further below.

In this question, vectors m through t are given in the figure. There are eight vectors : m, n, o, o', p, q, r, and s. The question asks to identify the groups of vectors that appear to be equal.

From the given figure, we can see that m and o' are parallel to each other and are of the same length. Thus, they are equal to each other. Also, vectors p and q are parallel to each other and are of the same length. So, they are equal to each other. Thus, we can conclude that m, o', p, and q are equal to each other.

Then, vectors n and r are parallel to each other and are of the same length . Thus, they are equal to each other. Also, vectors r and s are parallel to each other and are of the same length. So, they are equal to each other. Thus, we can conclude that n and r and s and r are equal to each other.

Therefore, the groups of vectors that appear to be equal are OB, m, o', p and qin, r, and s.

Learn more about Vectors .

brainly.com/question/29740341

Given the parametric curve x = e^t cost, y = e^t sint from t = 0 to t = 1. (a) Find the equation of the tangent line to the curve at t = 0. (b) Find the value(s) of t in 0, ] where the curve has a vertical or horizontal tangent line. (c) Find the length of the curve in the interval 0, 1].

The equation of tangent line at t=0 is y=x-1, the curve has vertical tangent lines at [tex]t=\frac{\pi}{4}+n(\frac{\pi}{2})[/tex]and horizontal tangent lines at[tex]t=\frac{3\pi}{4}+n(\frac\{pi}{2)}[/tex], and the length of the curve in the interval 0,1] is e-1.

(a) To find the equation of the tangent line at t = 0, we need to find the slope of the curve at that point.

Taking the derivatives of x and y with respect to t, we get:

[tex]\frac{dx}{dt} = e^t {(cos t - sin t)}[/tex]

[tex]\frac{dy}{dt} = e^t {(sin t + cos t)}[/tex]

At t = 0, we have x = 1 and y = 0. So, the slope of the tangent line at t = 0 is:

[tex]\frac{dy}{dx} = (\frac{dy}{dt}){(\frac{dx}{dt})} = \frac{(sin t + cos t)}{(cos t - sin t)}[/tex]

Plugging in t = 0, we get:

[tex]\frac{dy}{dx} = \frac{1}{1} = 1[/tex]

So, the equation of the tangent line at t = 0 is y = mx + b, where m = 1 is the slope and (1,0) is a point on the line. Solving for b, we get:

0 = 1(1) + b

Therefore, the equation of the tangent line to the curve at t = 0 is y = x - 1.

(b) To find where the curve has a vertical or horizontal tangent line, we need to find where [tex]\frac{dx}{dt}[/tex] = 0 or [tex]\frac{dy}{dt}[/tex] = 0.

Setting dx/dt = 0, we get:

e^t (cos t - sin t) = 0

This equation is satisfied when cos t = sin t, or when[tex]t =\frac {\pi}{4} + n(\frac{\pi}{2})[/tex] for any integer n. At these values of t, the slope of the curve is undefined and the tangent line is vertical.

Setting dy/dt = 0, we get:

[tex]e^t (sin t + cos t) = 0[/tex]

This equation is satisfied when sin t = -cos t, or when[tex]t = \frac{3\pi}{4} + n(\frac{\pi}{2})[/tex]for any integer n. At these values of t, the slope of the curve is 0 and the tangent line is horizontal.

Therefore, the curve has vertical tangent lines at [tex]t = \frac{\pi}{4} + n(\frac{\pi}{2})[/tex] and horizontal tangent lines at [tex]t = \frac{3\pi}4 + n(\frac{\pi}2)[/tex], for any integer n.

L = integral from a to b of [tex]\sqrt[(\frac{dx}{dt^2}) + (\frac{dy}{dt}^2)]dt[/tex]

Plugging in the expressions for [tex]\frac{dx}{dt}[/tex] and [tex]\frac{dy}{dt}[/tex], we get:

L = integral from 0 to 1 of [tex]\sqrt [e^ (2t)] dt[/tex]= integral from 0 to 1 of [tex]e^t dt[/tex]

Evaluating the integral, we get:

[tex]L = e^t[/tex]from 0 to 1 = e - 1

Therefore, the length of the curve in the interval 0, 1] is e - 1.

Learn more about tangent lines and parametric curve .

brainly.com/question/22029997

Saved The point of diminishing returns is always an inflection point of the production function. True False

The statement "The point of diminishing returns is always an inflection point of the production function" is False.

The point of diminishing returns refers to when an increase in input results in a smaller increase in output, while an inflection point is where the production function changes its concavity. These points may coincide, but it is not always the case. In economics, diminishing returns are the decrease in marginal output of a production process as the amount of a single factor of production is incrementally increased, holding all other factors of production equal. The law of diminishing returns (also known as the law of diminishing marginal productivity) states that in productive processes, increasing a factor of production by one unit, while holding all other production factors constant , will at some point return a lower unit of output per incremental unit of input.

Know more about Diminishing returns here:

https://brainly.com/question/14250273

Sadie has 44 m of fencing to build a three-sided fence around a rectangular plot of land that sits on a riverbank. (The fourth side of the enclosure would be the river.) The area of the land is 234 square meters. List each set of possible dimensions (length and width) of the field.

Therefore, the possible sets of dimensions (length and width) of the rectangular plot of land are: 11.142 m by 21 m and 10.565 m by 23 m.

Area is a measure of the amount of surface or space that a two-dimensional shape or figure occupies. It is usually expressed in square units, such as square meters (m²), square feet (ft²), square centimeters (cm²), and so on. The area of a shape or figure can be calculated using different formulas depending on its type. Area has several applications in mathematics, science, engineering, and everyday life. Area is also used to calculate quantities such as density, pressure, and flux, and to analyze and compare shapes and figures .

Let's denote the length and width of the rectangular plot of land as L and W, respectively. We know that the perimeter of the rectangular plot of land is 44 m, which means that:

2L + W = 44

We also know that the area of the rectangular plot of land is 234 square meters, which means that:

We can solve for one of the variables in terms of the other using the second equation, for example:

Substituting this expression for L into the first equation, we get:

2(234/W) + W = 44

Multiplying both sides by W, we get:

468/W + W² = 44W

Rearranging and simplifying, we get:

W³ - 44W² + 468W = 0

Factoring out W, we get:

W(W² - 44W + 468) = 0

So, we need to find the values of W that make either W or (W² - 44W + 468) equal to zero.

Setting W = 0, we get:

W(W² - 44W + 468) = 0(0² - 44(0) + 468) = 0

So, W = 0 is one solution.

To find the other solutions, we can solve the quadratic factor (W² - 44W + 468) = 0 using the quadratic formula:

W = (-b ± √(b² - 4ac)) / 2a

where a, b, and c are the coefficients of the quadratic in standard form (ax² + bx + c).

In this case, a = 1, b = -44, and c = 468, so we have:

W = (-(-44) ± √((-44)² - 4(1)(468))) / 2(1)

W = (44 ± √(4)) / 2

W = 21 or W = 23

To know more about area ,

https://brainly.com/question/22469440

1 1. Determine if the series (-1)*4k converges or diverges. If it converges k=1 5k - 1 approximate the sum S of the series to within 0.01. (5 pts) +1 -(-1)"+1 Determine if the series converges absolutely, converges conditionally, or n=1 vn diverges.

The given series is (-1)^n * (4n) with n starting from 1. To determine if the series converges or diverges, we can use the Alternating Series Test. For an alternating series, it converges if: 1. The terms are non-increasing: a_n+1 <= a_n for all n. 2. The limit of the terms as n goes to infinity is 0: lim(n→∞) a_n = 0. The terms a_n = 4n are increasing and not non-increasing, so the series diverges. Thus, we cannot approximate the sum S of the series to within 0.01. For the second part of the question, we check the absolute convergence by considering the series with absolute values of the terms: Σ(4n) with n starting from 1. This is a divergent arithmetic series, so the original series does not converge absolutely. Since the original series also diverges, we conclude that the series diverges.

The given series is (-1)*4k. To determine if it converges or diverges, we need to check if its terms approach zero as k goes to infinity. Since the absolute value of each term is 4k, which increases without bound as k goes to infinity, the series diverges. Next, if we assume k=1 5k - 1 and sum the first few terms of the series , we get: S = (-1)*4(1) + (-1)*4(2) + (-1)*4(3) + (-1)*4(4) + (-1)*4(5) + (-1)*4(6) + ... S = -4 -8 -12 -16 -20 -24 -... We can see that the sum of the series is -4 times the sum of the positive integers, which is a well-known formula with the value of -1/12. Therefore, the sum of the given series is 1/3. Finally, to determine if the series converges absolutely, converges conditionally, or diverges, we need to check if the absolute value of each term of the series converges or diverges. Since the absolute value of each term is 4k, which increases without bound as k goes to infinity, the series diverges. Therefore, the series converges conditionally.

Learn more about Converges :

brainly.com/question/9385279

4. Let r(t) F(t) = (14 = COS (1) t cost t t+tan(3t)' 1- Vt+1 6+1) Find lim r(t). t. > t-70

lim r(t) = 0 as t approaches negative infinity. This can be answered by the concept of Limit .

The question asks for the limit of r(t) as t approaches negative infinity.

To find the limit, we can use the fact that cosine and tangent are bounded functions and that the terms involving the square root and division by (t+1)² and (t-6)² become negligible as t approaches negative infinity . Therefore, we can simplify the expression for r(t) as:

r(t) = (14 - COS(t) + tan(3t)) / (t+1)²

As t approaches negative infinity, the numerator approaches 14 since both cosine and tangent have bounded values, and the denominator approaches infinity. Therefore, the limit of r(t) as t approaches negative infinity is zero.

Therefore, lim r(t) = 0 as t approaches negative infinity.

To learn more about Limit here:

brainly.com/question/30532698#

determine whether the series is convergent or divergent. [infinity] sum.gif n = 1 5 sqrt1a.gif n 1 + 5n3/2 Determine whether the series is convergent or divergent. [infinity] 7 n2 + 64 sum.gif n = 1 [infinity] sum.gif k = 1 ke−7

1. The first series converges. 2. The second series converges. 3. The third series converges.

1. For the first series , you have Σ (5/√(1 + 5n^(3/2))) from n = 1 to infinity. You can apply the Limit Comparison Test by comparing it with Σ (1/n^(3/4)) from n = 1 to infinity. Since the limit as n approaches infinity of (5/√(1 + 5n^(3/2))) / (1/n^(3/4)) is equal to 1, which is finite and positive, both series either converge or diverge together. Since Σ (1/n^(3/4)) is a convergent p-series with p > 1, the original series also converges. 2. For the second series, you have Σ (7/(n^2 + 64)) from n = 1 to infinity. By applying the Comparison Test , we can compare it with Σ (1/n^2) from n = 1 to infinity. Since 7/(n^2 + 64) ≤ 7/n^2, and Σ (1/n^2) is a convergent p-series with p > 1, the original series also converges by the Comparison Test. 3. For the third series, you have Σ (k * e^(-7k)) from k = 1 to infinity. In this case, you can apply the Integral Test . The integral from 1 to infinity of x * e^(-7x) dx converges, as it can be evaluated using integration by parts. Since the integral converges, the original series converges as well. For more such questions on Series.

https://brainly.com/question/15415793#

A napkin ring is being made of cast silver. It has the shape of a cylinder 1 inches high, with a cylindrical hole 1 inch in diameter and a thickness of 14 inch. How many ounces of silver are required? It will help to know that silver weighs about 6 ounces per cubic inch.

To find the volume of the silver needed for the napkin ring, we first need to calculate the volume of the outer cylinder and the inner cylinder (hole) separately, and then subtract the volume of the hole from the volume of the cylinder . Volume of outer cylinder: V = πr^2h V = π(0.5)^2(1) V = 0.785 cubic inches Volume of inner cylinder: V = πr^2h V = π(0.5)^2(1) V = 0.785 cubic inches Volume of silver needed: V = V(outer) - V(inner) V = 0.785 - 0.785 V = 0 cubic inches Since there is no volume of silver needed (the hole takes up the same amount of space as the outer cylinder ), we know that no silver is required to make the napkin ring. However, if we were to assume that the thickness of 14 inch refers to the height of the outer cylinder instead of the diameter , then we would get a non-zero volume and can calculate the amount of silver needed. Volume of outer cylinder: V = πr^2h V = π(0.5)^2(0.14) V = 0.0349065 cubic inches Volume of inner cylinder: V = πr^2h V = π(0.5)^2(0.14) V = 0.0349065 cubic inches Volume of silver needed: V = V(outer) - V(inner) V = 0.0349065 - 0.0349065 V = 0 cubic inches Again, we get a volume of 0 cubic inches , which means no silver is required to make the napkin ring. Therefore, the answer to the question is 0 ounces of silver.

Visit here to learn more about volume : https://brainly.com/question/1578538 #SPJ11

Show that E C[a,b] is measurable if and only if given >0 there exist closed set FcE and an open set G 3 E such that |Gl-|Fl < e

f is a continuous function in C[a, b] \ E. Then, for any ε > 0, there exists a closed set F or an open set G such that f ∈ F and f ∉ G, and hence |F − G| ≥ ε.

Let E ⊆ C[a, b] be a collection of continuous functions on the interval [a, b].

First, assume that E is measurable. Then, by definition, there exists a Borel σ-algebra B on C[a, b] such that E is a Borel set. Since the Borel σ-algebra is generated by the open sets in C[a, b], we can find a sequence of open sets {G_n} in C[a, b] such that G_n → E as n → ∞. Similarly, we can find a sequence of closed sets {F_n} in C[a, b] such that F_n → E as n → ∞. By the continuity of the functions in E, it follows that |G_n − E| → 0 and |F_n − E| → 0 as n → ∞. Thus, given any ε > 0, we can choose N such that |G_N − E| < ε/2 and |F_N − E| < ε/2, and let G = G_N and F = F_N. Then, |G − F| = |G − E + E − F| ≤ |G − E| + |E − F| < ε, and we have found the required closed set F and open set G.

Conversely, assume that for any ε > 0, there exist closed set F and open set G such that |G − F| < ε. Let H be the set of all open sets G in C[a, b] such that there exists a closed set F with |G − F| < ε. Then, H is a basis for a topology on C[a, b]. Let B be the Borel σ-algebra generated by this topology. It suffices to show that E is a Borel set in (C[a, b], B).

Since E is a collection of continuous functions, it follows that E is a subset of the set of all bounded functions on [a, b]. Let B_0 be the Borel σ-algebra generated by the uniform norm topology on the space of bounded functions on [a, b]. Since the uniform norm topology is finer than the topology generated by H, it follows that B_0 is contained in B.

Now, consider the set A of all functions f in C[a, b] such that there exists an open set G and a closed set F with f ∈ G and f ∉ F. Note that A is an open set in C[a, b]. We claim that E = C[a, b] \ A.

To see this, suppose that f is a continuous function in E. Then, there exists an open set G and a closed set F with f ∈ G and f ∉ F. Since G and F are disjoint, there exists ε > 0 such that the open ball of radius ε around f is contained entirely in G or entirely in the complement of F. Without loss of generality, assume that the ball is contained in G. Then, for any continuous function g such that |g − f| < ε/2, we have g ∈ G and g ∉ F, which implies that g is in E. Thus, E is an open set, and hence C[a, b] \ E is closed.

Similarly, suppose that f is a continuous function in C[a, b] \ E. Then, for any ε > 0, there exists a closed set F or an open set G such that f ∈ F and f ∉ G, and hence |F − G| ≥ ε.

To learn more about continuous function visit:https://brainly.com/question/21447009

rewrite the exprossion in the form b^n b^15/b

Answer: To rewrite the expression in the form b^n b^15/b, we can simplify the expression by combining the terms with the same base, which is b.

So, b^n b^15/b can be written as b^(n+15)/b.

Using the property of exponents, when we divide two exponential terms with the same base, we can subtract their exponents. Therefore, b^(n+15)/b can be simplified further as b^(n+15-1), which is equal to b^(n+14).

Hence, the given expression in the form b^n b^15/b is equivalent to b^(n+14).

Why do we minimize the e2 in order to find the best fitted line for bivariate data? Why not just minimizing ei? Why the following assumptions must be met in order for us to use linear regression? i. The errors 81,..,6n are random and independent. In particular, the magnitude of any error & does not influence the value of the next error &+1. ii. The errors a, ,an all have mean 0. iii, The errors ε ,G, all have the same variance, which we denote by σ. iv. The errorsare normally distributed.

In order to find the best-fitted line for bivariate data , we we minimize the sum of squared errors (e²) as it eliminates the positive and negative error issues and it is more sensitive to extreme values.

In order to use linear regression, the following assumptions must be met because i. the magnitude of any error εi does not influence the value of the next error εi+1. ii. it guarantees that the model is unbiased. iii. ensures that the model's predictions are equally reliable. iv. allows us to make statistical inferences.

To determine the best-fitted line for bivariate data , we minimize the sum of squared errors (e²) rather than just minimizing the individual errors (ei) because:

1. Squaring the errors eliminates the issue of positive and negative errors canceling each other out, ensuring that we focus on the total magnitude of the errors.

2. Minimizing the sum of squared errors is more sensitive to extreme values, allowing us to achieve a better overall fit to the data.

In order to use linear regression , the following assumptions must be met:

i. The errors (ε1, ..., εn) are random and independent, meaning that the magnitude of any error εi does not influence the value of the next error εi+1. This assumption ensures that the regression model is unbiased and that the errors do not follow a systematic pattern, which could lead to incorrect predictions.

ii. The errors (ε1, ..., εn) all have a mean of 0. This assumption guarantees that the model is unbiased, as it ensures that the overall error is not systematically over- or under-estimating the relationship between the variables.

iii. The errors (ε1, ..., εn) all have the same variance, denoted by σ². This assumption of homoscedasticity ensures that the model's predictions are equally reliable across the entire range of predictor values.

iv. The errors are normally distributed. This assumption allows us to make statistical inferences about the model parameters and predictions, as many statistical tests rely on the normality assumption for their validity.

Learn more about Bivariate data :

https://brainly.com/question/28730153

Eva invests $8000 in a new savings account which earns 4.8% annual interest, compounded semi-annually. What will be the value of her investment after 7 years? Round to the nearest cent.

The value of Eva's investment after 7 years will be $10,968 rounded to the nearest cent.

To calculate the value of Eva's investment after 7 years, we first need to determine the interest rate per compounding period. Since the interest is compounded semi-annually (twice per year), we divide the annual interest rate by 2: 4.8% / 2 = 2.4% Next, we need to determine the number of compounding periods over 7 years. Since the interest is compounded twice per year, we multiply the number of years by 2: 7 years x 2 = 14 compounding periods Now we can use the formula for compound interest: A = P(1 + r/n)^(nt) Where: A = the future value of the investment P = the principal amount (initial investment) r = the annual interest rate (as a decimal ) n = the number of times the interest is compounded per year t = the number of years Plugging in the values, we get: A = 8000(1 + 0.024/2)^(2*14) A = 8000(1.012)^28 A = 8000(1.371) A = 10968

Know more about investment here:

https://brainly.com/question/15353704

Part 1. Determine the molar mass of a 0.622-gram sample of gas having a volume of 2.4 L at 287 K and 0.850 atm. Show your work. Part 2. If this sample was placed under extremely low temperature, describe how the actual volume would compare to the predicted volume. Explain your answer.

Part 1: The molar mass is 727. 49 g/mol

Part 2: If the small temperature reduces, the actual volume of the sample also reduces

Following the ideal gas rule;

Given that;

Substitute the values

n = 0. 850 × 2.4/8. 3145 × 287

Multiply the values

n = 2. 04/2386. 26

Divide the values

n = 8. 55 × 10^-4

n = mass/molar mass

molar mass = mass/n = 0. 622/8. 55 × 10^-4 = 727. 49 g/mol

Learn more about Ideal gas law at: https://brainly.com/question/25290815

in testing for differences between the means of two related populations, the null hypothesis is h0 : µd = 2 h0 : µd = 0 h0 : µd < 0 h0 : µd > 0

When testing for differences between the means of two related populations, the null hypothesis is h0: µd = 0.

What is the testing for differences between the means of two related populations?

Two related populations are being tested for differences between their means in this scenario.

In other words, the hypothesis testing investigates if the mean difference between two paired data is significantly different from zero.

In the null hypothesis, it is usually assumed that the mean difference is zero .What is a null hypothesis?

A null hypothesis is a statement that is made in statistics to specify that there is no real difference between two parameters or that a certain value is unknown. In hypothesis testing, the null hypothesis is compared to an alternative hypothesis, and a decision is made based on the statistical analysis. It is also referred to as the status quo or the default assumption.

The null hypothesis is h0: µd = 0.

To learn more about null hypothesis visit: brainly.com/question/29892401

Consider the function f(x) = 1/x on the interval [2,7]. Find the average or mean slope of the function on this interval. By the Mean Value Theorem, we know there exists a c in the open interval (2, 7) such that f'(c) is equal to this mean slope. For this problem, there is only one that works. Find it.

There is only one value that works for this problem: c = sqrt(14) in the open interval (2, 7), such that f'(c) is equal to the mean slope of -1/14.

To find the average or mean slope of the function f(x) = 1/x on the interval [2,7], we need to follow these steps: 1. Calculate f(7) and f(2): f(7) = 1/7 f(2) = 1/2 2. Find the difference in the function values and divide by the difference in the x values to find the average slope: (f(7) - f(2)) / (7 - 2) = (1/7 - 1/2) / (5) = (-5/14) / 5 = -1/14 3. Use the Mean Value Theorem : According to the Mean Value Theorem, there exists a c in the open interval (2, 7) such that f'(c) is equal to the mean slope. 4. Find f'(x): To find f'(x), we need to differentiate f(x) = 1/x. f'(x) = -1/[tex]x^2[/tex] 5. Set f'(c) equal to the mean slope and solve for c: -1/[tex]c^2[/tex] = -1/14 [tex]c^2[/tex] = 14 c = sqrt(14) So, there is only one value that works for this problem: c = sqrt(14) in the open interval (2, 7), such that f'(c) is equal to the mean slope of -1/14.

To know more about " Slope " refer here:

https://brainly.com/question/6501549#

Assume x and y are functions of t. Evaluate dy/dt. x^3 = 19y^5-11 ; dx/dt = 19/2, y = 1

The value of dy/dt is[tex](3/190)(19-11)^3 = (3/190)(8)^3 = 0.1027[/tex](approx)

x and y are both functions of t, we need to use implicit differentiation to find the derivative of y with respect to t. We start by taking the derivative of both sides of the given equation with respect to t .

We need to use implicit differentiation to find dy/dt. Taking the derivative of both sides with respect to t, we get:

[tex]3x^2(dx/dt) = 95y^4(dy/dt)[/tex]

Substituting the given values of dx/dt and y, we get:

[tex]3(x^3)/2 = 95(1)^4(dy/dt)[/tex]

Simplifying, we get:

[tex]dy/dt = (3/190)(x^3)[/tex]

Substituting the given value of x, we get:

[tex]dy/dt = (3/190)(19y^5-11)^3[/tex]

Therefore, the value of dy/dt is [tex](3/190)(19-11)^3 = (3/190)(8)^3 = 0.1027[/tex](approx).

To learn more about differentiation visit: https://brainly.com/question/24898810

Devising recursive definitions for sets of strings. Let A = {a, b}. (c) Let S be the set of all strings from A* in which there is no b before an a. For example, the strings λ, aa, bbb, and aabbbb all belong to S, but aabab ∉ S. Give a recursive definition for the set S. (Hint: a recursive rule can concatenate characters at the beginning or the end of a string.)

The set S of all strings in which there is no b before an a, we can use a recursive definition . We start with the empty string λ, which is a member of S.

We can see that this definition works by considering how it handles strings with b's and a's. If a string has a b before an a, then it cannot be in S, since the rule only allows a's to be added before or after the string.

Conversely, if a string does not have a b before an a, we can apply the rule to add a's before or after the string until it reaches S. In summary, the recursive definition for the set S of all strings in which there is no b before an a is: Then, we can define a rule that says that if s is in S, then as and sa are also in S. This rule works because it concatenates an a onto the beginning or end of the string, ensuring that there is no b before the a. Base case: λ is in S. Recursive rule: If s is in S, then as and sa are also in S.

for such more questions on strings

https://brainly.com/question/31250964

Bryan's lemon cookie recipe calls for 1 1/3 cups of sugar. How much sugar would Bryan use to make 3 1/2 batches of cookies?

4 2/3 cups of sugar

Step-by-step explanation:

1 1/3 x 3 1/2 = 4 2/3

If a bridge has a chord length of 3 feet, and an arch length of 4 feet, what is the height of the arc?

To find the height of the arc , we need to use the formula for the height of a circular segment. First, we can find the radius of the circle using the chord length and the arch length. So the height of the arc is approximately 0.38 feet. Let's call the radius "r" . We know that the arch length is 4 feet and that this length is equal to the circumference of the circle, which is 2πr . So we can set up an equation: 2πr = 4 Dividing both sides by 2π, we get: r = 2/π Now we can use the formula for the height of a circular segment: height of arc = r - √(r^2 - (chord length/2)^2) Plugging in the values we have: height of arc = 2/π - √((2/π)^2 - (3/2)^2) Simplifying and using a calculator, we get: height of arc ≈ 0.38 feet So the height of the arc is approximately 0.38 feet.

To find the height of the arc for a bridge with a chord length of 3 feet and an arch length of 4 feet, follow these steps: 1. Determine the radius (r) of the circle that creates the arc using the formula: Arch length = r * θ (where θ is the central angle in radians) 2. Since we don't have θ, we can use the relationship between the chord length, radius, and θ: Chord length = 2 * r * sin(θ/2) 3. Combine both formulas to find θ: θ = Arch length / r = 2 * asin(Chord length / (2 * r)) 4. Solve for r using the given values for the chord length (3 feet) and arch length (4 feet): θ = 2 * asin(3 / (2 * r)) 4 / r = 2 * asin(3 / (2 * r)) 5. After solving for r numerically, you'll find r ≈ 2.08 feet. 6. Now, find the height of the arc using the radius and the chord length. Draw a right triangle by dropping a perpendicular line from the center of the circle to the midpoint of the chord. The height (h) is the difference between the radius (r) and the length of this perpendicular line. 7. Use the Pythagorean theorem to find the length of the perpendicular line: (Perpendicular line)^2 + (Chord length / 2)^2 = r^2 8. Plug in the values and solve for the perpendicular line: (Perpendicular line)^2 + (1.5)^2 = (2.08)^2 Perpendicular line ≈ 1.66 feet 9. Finally, find the height of the arc: Height of the arc = Radius - Perpendicular line Height of the arc = 2.08 - 1.66 ≈ 0.42 feet So, the height of the arc for the bridge with a chord length of 3 feet and an arch length of 4 feet is approximately 0.42 feet.

Visit here to learn more about arc:

brainly.com/question/18741430

Ethan bought 2 action figures for $25 each at a science fiction fair. He won an auction for a plastic sword, and he got a deal on 5 comic books for $9 each. He spent $102 altogether. How much did Ethan pay for the plastic sword?

Ethan paid 2 * $25 = $50 for the action figures.

The comic books cost 5 * $9 = $45.

So, Ethan paid $50 + $45 = $95 for the action figures and comic books.

The plastic sword cost $102 - $95 = $7.

So the answer is 7

faz? 1403 + 712 +271 +27 Consider the indefinite integral de 24 + 922 Then the integrand has partial fractions decomposition ь CE +d + + 12 + 9 where a T Wh a = b = C= d = = Integrating term by term, we obtain that 1423 + 7.2 + 270 + 27 24 + 922 dx = Question Help: D Video Submit Question

The sum of the numbers is 2413. The indefinite integral of (24 + 922) dx is: [tex]24x + 461x^2 + C[/tex]

It seems like there are two separate questions here. Let me answer them one by one. To find the sum of the numbers 1403, 712, 271, and 27, simply add them together: 1403 + 712 + 271 + 27 ----- 2413 So, the sum of these numbers is 2413. For the indefinite integral question, it appears some information is missing. However, I'll provide some guidance based on what's provided. You're asked to consider the indefinite integral of the function 24 + 922.

Consider the indefinite integral of (24 + 922) dx. ∫(24 + 922) dx Separate the terms. = ∫24 dx + ∫922 dx Integrate each term with respect to x. =[tex]24x + 922x^2/2 + C[/tex] (C is the constant of integration) Thus, the indefinite integral of (24 + 922) dx is: [tex]24x + 461x^2 + C[/tex]

The goal is to find the partial fraction decomposition of the integrand. The given integrand is not in the form of a rational function, so it's not clear how to proceed with partial fractions decomposition. If you provide more information about the integrand or clarify the question, I'll be happy to help further. For now, the first question has been answered, and the sum of the numbers is 2413.

for more questions on indefinite integral

https://brainly.com/question/22008756

Find all the first order partial derivatives for the following function. f(x.y.z)=z(e^X)^y

The first-order partial derivatives of f(x,y,z) are:

[tex]\partial f/\partial x = zy(e^x)^y-1 * e^x[/tex]

[tex]\partial f/ \partial y = ze^x^y * ln(e^x)[/tex]

[tex]\partial f/ \partial z = e^x^y[/tex]

To find the first-order partial derivatives of the function [tex]f(x,y,z) = z(e^x)^y,[/tex]we differentiate the function with respect to each variable separately while holding the other variables constant .

To find this derivative, we use the product rule, where[tex]u = zy(e^x)^y-1[/tex] and [tex]v = e^x,[/tex] so that:

[tex]\partial f/ \partial x = u'v + uv' = (zy(e^x)^y-1)' e^x + zy(e^x)^y-1 (e^x)' = zy(e^x)^y-1 * e^x[/tex]

To find this derivative, we use the chain rule , where [tex]u = e^x^y[/tex] and v = z, so that:

[tex]\partial f/ \partial y = u'v = ze^x^y * ln(e^x)[/tex]

To find this derivative, we simply differentiate z with respect to z, which gives:

[tex]\partial f/\partial z = e^x^y[/tex]

Therefore, the first-order partial derivatives of f(x,y,z) are:

Learn more about first-order partial derivatives

brainly.com/question/30884117

7. The radius r and the height h of a right circular cone are always equal. Find the rate of change of the volume of the cone with respect to h.

The rate of change of the volume of the cone with respect to h is equal to πr².Since r and h are equal, we can substitute r for h. Therefore, the rate of change of the volume of the cone with respect to h is equal to πh².

This means that as the height of the cone increases, the volume increases at a faster rate . For example, if the height of the cone increases by 1 unit, the volume will increase by π units. In simpler terms, the rate of change of the volume of the cone with respect to h is how quickly the volume of the cone changes as the height of the cone changes. In this case, since the radius and height are equal, the rate of change is equal to πh². This means that as the height increases , the volume of the cone increases at a faster rate.

To know more about volume click on below link:

https://brainly.com/question/29767724#

I need help question in picture

It should be noted that calculating the measure of the third one is possible by subtracting the measure of the amalgamated angle with those two known angles .

Forming an angle comprised of three minor angles, we are able to utilize the truth that their total is equal to the measurement of the composite angle.

Therefore, if we have knowledge of any two of these embedded angles, calculating the measure of the third one is possible by subtracting the measure of the amalgamated angle with those two known angles.

The alteration in angle regarding the serpent's mouth is analogous to the disparity between the beginnings and final angles: or 180° - 60° = 120°.

Learn more about angle on

https://brainly.com/question/25716982

(r – 1)(r – 3) = 0 Solve the quadratic equation by factoring

Simplify the expression. Write your answer is standard form. −4d(5d2−12)+7(d+5)

[tex]-20d^3 + 55d + 35[/tex]t is the simplified expression in standard form.

First, distribute the -4d across the parentheses :

[tex]-4d(5d^2-12) = -20d^3 + 48d[/tex]

Then distribute the 7 across the parentheses:

[tex]7(d+5) = 7d + 35[/tex]

Putting these together, we get:

[tex]-4d(5d^2-12)+7(d+5) = -20d^3 + 48d + 7d + 35[/tex]

Combining like terms, we get:

[tex]-20d^3 + 55d + 35[/tex]

Therefore, the simplified expression in standard form is:

Learn more about Simplification here:

https://brainly.com/question/28996879

Complete Question:

Simplify the expression. Write your answer in a standard form.

[tex]-4d(5d^2-12)+7(d+5)[/tex]

which of the following is the equation of a line perpendicular to the line y=-3/2x+4 passng through the point (3,9)

The required equation of a line perpendicular to the line y=-3/2x+4 passing through the point (3,9) is y = 2/3x + 7.

The given line has a slope of -3/2. The slope of a line perpendicular to this line will be the -ve reciprocal of -3/2, which is 2/3. We can use the point-slope form of the equation of a line to find the equation of the line that passes through the point (3,9) with a slope of 2/3: |y - 9 = 2/3(x - 3)

Simplifying and rearranging this equation to the slope-intercept form (y = mx + b) gives: y = 2/3x + 7

Learn more about the equation of line here:

https://brainly.com/question/31086219

Verify that the function f(x) = ln x satisfies the hypotheses of the Mean Value Theorem on the given interval [1,4]. Then find all numbers c that satisfy the conclusion of the Mean Value Theorem.

The f(x) = ln(x) satisfies the hypotheses of the (MVT) on the interval [1, 4], the interval (1, 4) that satisfies the conclusion of the MVT, and c = 3 / ln(4).

the function must be continuous and differentiable on the given interval. 1. Continuity: The natural logarithm function , ln(x), is continuous for all positive x values. Since the interval [1, 4] only contains positive values, f(x) = ln(x) is continuous on this interval. 2. Differentiability: The derivative of

[tex]f(x) = ln(x) is f'(x) = 1/x.[tex]

The function 1/x is differentiable for all non-zero x values. Again, the interval [1, 4] has no zeros, so f(x) = ln(x) is differentiable on this interval. [tex]f'(c) = (f(b) - f(a)) / (b - a)[/tex] In our case, a = 1 and b = 4. So, we need to find f(1), f(4), and f'(x): [tex]f(1) = ln(1) = 0[/tex] [tex]f(4) = ln(4)[/tex] [tex]f'(x) = 1/x[/tex] Now, we can set up the MVT equation: [tex]1/c = (ln(4) - 0) / (4 - 1)[/tex] [tex]1/c = ln(4) / 3[/tex] To find c, we can take the reciprocal of both sides: [tex]c = 3 / ln(4)[/tex] Therefore, there exists a number c in the interval (1, 4) that satisfies the conclusion of the MVT, and c = 3 / ln(4).

for such more questions on logarithm function

https://brainly.com/question/13473114

(1 point) Find the most general antiderivative P of p(s) = 4 sin(4s). P(s) II NOTE: Don't forget the constant in your answer.

The most general antiderivative of p(s) = 4 sin(4s) is P(s) = (-1/4) cos(4s) + C, where C is any constant .

To find the most general antiderivative of p(s) = 4 sin(4s), we can integrate it with respect to s using the power rule for integration. The power rule states that the antiderivative of x^n is (1/(n+1))x^(n+1) + C, where C is the constant of integration. Applying the power rule to p(s) = 4 sin(4s), we get P(s) = (-1/4) cos(4s) + C, where C is the constant of integration. We can check that this is indeed the antiderivative by taking its derivative and verifying that it equals p(s). This means that there are infinitely many antiderivatives of p(s), all of which differ by a constant. The constant represents the arbitrary integration constant that arises when we integrate a function, and its value can only be determined by additional information such as initial or boundary conditions.

To learn more about : constant

https://brainly.com/question/25215474

IMAGES

Significance Level and Power of a Hypothesis Test Tutorial
An easy-to-understand summary of significance level
Understanding Hypothesis Tests: Significance Levels (Alpha) and P
PPT
Significance Level and Power of a Hypothesis Test Tutorial
PPT

VIDEO

Testing of Hypothesis|Null & Alternative hypothesis|Level Of Significance|Critical Region|Lecture 22
Hypothesis Testing
Hypothesis Testing
Lesson for 7 1 Hypothesis Testing introduction
Elements of Testing of Hypothesis
Statistics: Ch 9 Hypothesis Testing (29 of 35) Confidence Limits at a Smaller Sample Size

COMMENTS

How Hypothesis Tests Work: Significance Levels (Alpha) and P values
Hypothesis testing is a vital process in inferential statistics where the goal is to use sample data to draw conclusions about an entire population.In the testing process, you use significance levels and p-values to determine whether the test results are statistically significant.
Understanding Significance Levels in Statistics
Learn more about Statistical Significance: Definition & Meaning.. Changing Significance Levels. Because 0.05 is the standard alpha, we'll start by adjusting away from that value. Typically, you'll need a good reason to change the significance level to something other than 0.05.
Understanding Hypothesis Tests: Significance Levels (Alpha) and P
What do significance levels and P values mean in hypothesis tests? What is statistical significance anyway?In this post, I'll continue to focus on concepts and graphs to help you gain a more intuitive understanding of how hypothesis tests work in statistics.
Level of Significance & Hypothesis Testing
In hypothesis testing, the level of significance is a measure of how confident you can be about rejecting the null hypothesis. This blog post will explore what hypothesis testing is and why understanding significance levels are important for your data science projects. In addition, you will also get to test your knowledge of level of significance towards the end of the blog with the help of quiz.
Significance tests (hypothesis testing)
Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values to make conclusions about hypotheses.
Hypothesis Testing, P Values, Confidence Intervals, and Significance
Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting ...
An Easy Introduction to Statistical Significance (With Examples)
An Easy Introduction to Statistical Significance (With Examples) Published on January 7, 2021 by Pritha Bhandari.Revised on June 22, 2023. If a result is statistically significant, that means it's unlikely to be explained solely by chance or random factors.In other words, a statistically significant result has a very low chance of occurring if there were no true effect in a research study.
Hypothesis Testing
Hypothesis Testing (cont...) Hypothesis Testing The null and alternative hypothesis. In order to undertake hypothesis testing you need to express your research hypothesis as a null and alternative hypothesis.
5.1
A test is considered to be statistically significant when the p-value is less than or equal to the level of significance, also known as the alpha ($\alpha$) level.For this class, unless otherwise specified, $\alpha=0.05$; this is the most frequently used alpha level in many fields.
Hypothesis Testing
Step 5: Present your findings. The results of hypothesis testing will be presented in the results and discussion sections of your research paper, dissertation or thesis.. In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p-value).
Significance levels: what, why, and how?
Hypothesis Testing explained in 4 parts. Hypothesis Testing often confuses data scientists due to mixed teachings on p-values and significance testing.
Hypothesis Testing and Confidence Intervals
Read the companion post for this one: How Hypothesis Tests Work: Significance Levels (Alpha) and P-values.In that post, I use the same graphical approach to illustrate why we need hypothesis tests, how significance levels and P-values can determine whether a result is statistically significant, and what that actually means.
7.5: Critical values, p-values, and significance level
No headers. A low probability value casts doubt on the null hypothesis. How low must the probability value be in order to conclude that the null hypothesis is false?
Tests of Significance
Significance Levels The significance level for a given hypothesis test is a value for which a P-value less than or equal to is considered statistically significant. Typical values for are 0.1, 0.05, and 0.01. These values correspond to the probability of observing such an extreme value by chance. In the test score example above, the P-value is 0.0082, so the probability of observing such a ...
Using P-values to make conclusions (article)
Do you know how to use P-values to make conclusions about statistical significance? In this article, you will learn how to interpret P-values and compare them with a significance level. You will also see some examples of how P-values can help you decide whether to reject or fail to reject a null hypothesis. Khan Academy is a free online platform that offers you a world-class education in math ...
Understanding P-Values and Statistical Significance
The p-value in statistics quantifies the evidence against a null hypothesis. A low p-value suggests data is inconsistent with the null, potentially favoring an alternative hypothesis. Common significance thresholds are 0.05 or 0.01.
P-values and significance tests (video)
We compare a P-value to a significance level to make a conclusion in a significance test. Given the null hypothesis is true, a p-value is the probability of getting a result as or more extreme than the sample result by random chance alone.
Level of Significance (Statistical Significance)
The level of significance is defined as the fixed probability of wrong elimination of null hypothesis when in fact, it is true. Visit BYJU'S to learn the definition, steps and examples.
Hypothesis Testing: Upper-, Lower, and Two Tailed Tests
We now use the five-step procedure to test the research hypothesis that the mean weight in men in 2006 is more than 191 pounds. We will assume the sample data are as follows: n=100, =197.1 and s=25.6. Step 1.
5.1.1 Hypothesis Testing
How do we decide whether to reject or accept the null hypothesis? The null hypothesis would be rejected if the p - value is less than the significance level or if the test statistic falls within the critical region. The p - value is the probability of a value being at least as extreme as the test statistic, assuming that the null hypothesis is true. If the test is looking for a decrease then ...
Hypothesis Testing explained in 4 parts
Hypothesis Testing often confuses data scientists due to mixed teachings on p-values and significance testing. This article clarifies 10 key concepts with visuals and intuitive explanations.
Understanding Hypothesis Testing
If the p-value is less than or equal to the significance level i.e. ([Tex]p\leq\alpha [/Tex]), you reject the null hypothesis.This indicates that the observed results are unlikely to have occurred by chance alone, providing evidence in favor of the alternative hypothesis.
Hypothesis testing and p-values (video)
Why are you not using a t-distribution to find the probability of getting the sample result? I know that when the sample size is large (n = 100), a t-distribution is essentially the same as a normal distribution, but I think this lesson can be misleading when we are taught to use a t-distribution in the common case when the population standard deviation is not known and we are estimating it ...
Tests of Significance: Process, Example and Type
Step 1: Start by coming up with a research idea or question for your thesis. Step 2: Create a neutral comparison to test against your hypothesis. Step 3: Decide on the level of certainty you need for your results, which affects the type of sign language translators and communication methods you'll use. Step 4: Choose the appropriate statistical test to analyze your data accurately.
If The Cost Of A Type I Error Is High, A Smaller Value Should Be Chosen
The required equation of a line perpendicular to the line y=-3/2x+4 passing through the point (3,9) is y = 2/3x + 7.. The given line has a slope of -3/2. The slope of a line perpendicular to this line will be the -ve reciprocal of -3/2, which is 2/3.We can use the point-slope form of the equation of a line to find the equation of the line that passes through the point (3,9) with a slope of 2/3: