
Machine Learning
Artificial Intelligence
Control System

Supervised Learning
Classification, miscellaneous, related tutorials.
Interview Questions
| The hypothesis is a common term in Machine Learning and data science projects. As we know, machine learning is one of the most powerful technologies across the world, which helps us to predict results based on past experiences. Moreover, data scientists and ML professionals conduct experiments that aim to solve a problem. These ML professionals and data scientists make an initial assumption for the solution of the problem. This assumption in Machine learning is known as Hypothesis. In Machine Learning, at various times, Hypothesis and Model are used interchangeably. However, a Hypothesis is an assumption made by scientists, whereas a model is a mathematical representation that is used to test the hypothesis. In this topic, "Hypothesis in Machine Learning," we will discuss a few important concepts related to a hypothesis in machine learning and their importance. So, let's start with a quick introduction to Hypothesis. It is just a guess based on some known facts but has not yet been proven. A good hypothesis is testable, which results in either true or false. : Let's understand the hypothesis with a common example. Some scientist claims that ultraviolet (UV) light can damage the eyes then it may also cause blindness. In this example, a scientist just claims that UV rays are harmful to the eyes, but we assume they may cause blindness. However, it may or may not be possible. Hence, these types of assumptions are called a hypothesis. The hypothesis is one of the commonly used concepts of statistics in Machine Learning. It is specifically used in Supervised Machine learning, where an ML model learns a function that best maps the input to corresponding outputs with the help of an available dataset. There are some common methods given to find out the possible hypothesis from the Hypothesis space, where hypothesis space is represented by and hypothesis by Th ese are defined as follows: It is used by supervised machine learning algorithms to determine the best possible hypothesis to describe the target function or best maps input to output. It is often constrained by choice of the framing of the problem, the choice of model, and the choice of model configuration. . It is primarily based on data as well as bias and restrictions applied to data. Hence hypothesis (h) can be concluded as a single hypothesis that maps input to proper output and can be evaluated as well as used to make predictions. The hypothesis (h) can be formulated in machine learning as follows: Where, Y: Range m: Slope of the line which divided test data or changes in y divided by change in x. x: domain c: intercept (constant) : Let's understand the hypothesis (h) and hypothesis space (H) with a two-dimensional coordinate plane showing the distribution of data as follows: Hypothesis space (H) is the composition of all legal best possible ways to divide the coordinate plane so that it best maps input to proper output. Further, each individual best possible way is called a hypothesis (h). Hence, the hypothesis and hypothesis space would be like this: Similar to the hypothesis in machine learning, it is also considered an assumption of the output. However, it is falsifiable, which means it can be failed in the presence of sufficient evidence. Unlike machine learning, we cannot accept any hypothesis in statistics because it is just an imaginary result and based on probability. Before start working on an experiment, we must be aware of two important types of hypotheses as follows: A null hypothesis is a type of statistical hypothesis which tells that there is no statistically significant effect exists in the given set of observations. It is also known as conjecture and is used in quantitative analysis to test theories about markets, investment, and finance to decide whether an idea is true or false. An alternative hypothesis is a direct contradiction of the null hypothesis, which means if one of the two hypotheses is true, then the other must be false. In other words, an alternative hypothesis is a type of statistical hypothesis which tells that there is some significant effect that exists in the given set of observations.The significance level is the primary thing that must be set before starting an experiment. It is useful to define the tolerance of error and the level at which effect can be considered significantly. During the testing process in an experiment, a 95% significance level is accepted, and the remaining 5% can be neglected. The significance level also tells the critical or threshold value. For e.g., in an experiment, if the significance level is set to 98%, then the critical value is 0.02%. The p-value in statistics is defined as the evidence against a null hypothesis. In other words, P-value is the probability that a random chance generated the data or something else that is equal or rarer under the null hypothesis condition. If the p-value is smaller, the evidence will be stronger, and vice-versa which means the null hypothesis can be rejected in testing. It is always represented in a decimal form, such as 0.035. Whenever a statistical test is carried out on the population and sample to find out P-value, then it always depends upon the critical value. If the p-value is less than the critical value, then it shows the effect is significant, and the null hypothesis can be rejected. Further, if it is higher than the critical value, it shows that there is no significant effect and hence fails to reject the Null Hypothesis. In the series of mapping instances of inputs to outputs in supervised machine learning, the hypothesis is a very useful concept that helps to approximate a target function in machine learning. It is available in all analytics domains and is also considered one of the important factors to check whether a change should be introduced or not. It covers the entire training data sets to efficiency as well as the performance of the models. Hence, in this topic, we have covered various important concepts related to the hypothesis in machine learning and statistics and some important parameters such as p-value, significance level, etc., to understand hypothesis concepts in a better way. |

- Send your Feedback to [email protected]
Help Others, Please Share

Learn Latest Tutorials
Transact-SQL
Reinforcement Learning
R Programming
React Native
Python Design Patterns
Python Pillow
Python Turtle
Preparation

Verbal Ability

Company Questions
Trending Technologies
Cloud Computing
Data Science
B.Tech / MCA
Data Structures
Operating System
Computer Network
Compiler Design
Computer Organization
Discrete Mathematics
Ethical Hacking
Computer Graphics
Software Engineering
Web Technology
Cyber Security
C Programming
Data Mining
Data Warehouse

Intro to Machine Learning
This lecture will be a broad introduction to machine learning, framed in the context of specifying three separate aspects of machine learning algorithms. We will first cover a broad introduction to the idea of (supervised machine learning), define some notation on the topic, and then finally define the three elements of a machine learning algorithm: the hypothesis class, the loss function, and optimization methods.
The Three Ingredients of Machine Learning Algorithms
Despite the seemingly vast number of machine learning algorithms, they all share a common framework that consists of three key ingredients: the hypothesis class, the loss function, and the optimization method. Understanding these three components is essential for situating the wide range of machine learning algorithms into a common framework.
Hypothesis Class : This is the set of all functions that the algorithm can choose from when learning from the data. For example, in the case of linear classification, the hypothesis class would consist of all linear functions.
Loss Function : The loss function measures the discrepancy between the predicted outputs of the model and the true outputs. It guides the learning algorithm by providing a metric for the quality of a particular hypothesis.
Optimization Method : This refers to the algorithm used to search through the hypothesis class and find the function that minimizes the loss function. Common optimization methods include gradient descent and its variants.
By specifying these three ingredients for a given task, one can define a machine learning algorithm. These ingredients are foundational to all machine learning algorithms, whether they are decision trees, boosting, neural networks, or any other method.
Running Example: Multi-class Linear Classification
The running example used throughout the lecture series is multi-class linear classification. This example serves as a practical application of the concepts of supervised machine learning. It involves classifying images into categories based on their pixel values. For instance, an image of a handwritten digit is represented as a vector of pixel values, and the goal is to classify it as one of the possible digit categories (0 through 9).
In multi-class linear classification, the hypothesis class consists of linear functions, the loss function could be something like the softmax loss, and the optimization method could be stochastic gradient descent (SGD). This example will be used to illustrate the general principles of machine learning and will be implemented in code to provide a hands-on understanding of the concepts.
Supervised Machine Learning
Machine learning offers an alternative approach to classical programming. Instead of manually encoding the logic for digit recognition, machine learning relies on providing a large set of examples of the desired input-output mappings. The machine learning algorithm then “figures out” the underlying logic from these examples.
Supervised machine learning, in particular, involves collecting numerous examples of digits, each paired with its correct label (e.g., a collection of images of the digit ‘5’ labeled as ‘5’). This collection of labeled examples is known as the training set. The training set is fed into a machine learning algorithm, which processes the data and learns to map new inputs to their appropriate outputs.
The process of machine learning is sometimes described as data-driven programming. Rather than specifying the logic explicitly, the programmer provides examples of the input-output pairs and lets the algorithm deduce the patterns and rules that govern the mapping. This approach can handle the variability and complexity of real-world data more effectively than classical programming.
Training Set and Machine Learning Algorithm
The training set is a crucial component of supervised machine learning. It consists of numerous examples of inputs (e.g., images of digits) along with their corresponding outputs (the actual digits they represent). The machine learning algorithm uses this training set to learn the patterns and features that are predictive of the output.
The machine learning algorithm itself can be thought of as a “black box” that takes the training set and produces a model capable of making predictions on new, unseen data. The specifics of how the algorithm learns from the training set and what kind of model it produces will be discussed in further detail throughout the course.
Digit Classification and Language Modeling
Two primary examples of machine learning tasks are digit classification and language modeling. In digit classification, the goal is to classify images of handwritten digits into their corresponding numerical categories. Language modeling, on the other hand, deals with predicting the next word in a sequence given the beginning of a sentence. For example, given the input “the quick brown,” the model should predict the next word, such as “fox.”
Despite the apparent differences between images and text, machine learning algorithms can treat them similarly by operating on vector representations of the data. This approach allows for a unified treatment of various types of data.
Notation and Vector Representation
Inputs in machine learning algorithms are represented as vectors, denoted by \(x \in \mathbb{R}^n\) , which reside in an \(n\) -dimensional space. This means that each input vector is a collection of \(n\) real-valued numbers. For instance, an example of such a vector could be \[ x = \begin{bmatrix} 0.1 \\ 0 \\ -5 \\ \end{bmatrix}. \]
To refer to individual elements within this vector, subscripts are used. For example, \(x_2\) denotes the second element of the vector \(x\) . In general \(x_j\) represents the \(j\) -th element of the vector.
Training and Evaluation Sets
In practice, machine learning algorithms work with not just a single input but a set of inputs known as a training set. To denote different vectors within a training set, superscripts enclosed in parentheses are used. For example, \(x^{(i)}\) represents the \(i\) -th vector in the training set, where \(i\) ranges from \(1\) to \(m\) . Here, \(m\) is the number of training examples, and \(n\) is the dimensionality of the input space.
Target Vectors
The targets or outputs, denoted by \(y\) , correspond to the desired outcome for each input. In a multi-class classification setting, which is the focus of this discussion, the targets are a set of \(k\) numbers. Each output \(y^{(i)}\) is associated with an input vector \(x^{(i)}\) and is a discrete number in the set \(\{1, 2, ..., k\}\) , where \(k\) is the number of possible classes. The evaluation set, often referred to as the test set, is another collection of ordered pairs, denoted as \(\bar{x}^{(i)}, \bar{y}^{(i))}\) , where \(i\) ranges from 1 to \(\bar{m}\) . The vectors \(\bar{x}^{(i)}\) are in the same space \(\mathbb{R}^n\) , and the targets \(\bar{y}^{(i)}\) are from the same discrete set 1 to \(k\) . The evaluation set is used to assess the performance of the machine learning model.
Multiple different settings are possible depending on the type of target:
- Multi-class Classification : This is the scenario where there are multiple classes, and each input is classified into one of these classes. For example, in digit recognition, there are 10 classes (digits 0 through 9).
- Binary Classification : A special case of classification where there are only two classes. It is distinct enough to have its own name.
- Regression : If the target is a real value, the problem is referred to as regression. There are also more complex forms such as multi-value or vector-value regression and structured prediction, which deals with complex structured output spaces.
It is important to note that while modern AI may seem to produce complex outputs like paragraphs, the underlying algorithms often operate by outputting simpler elements, like one word at a time, which collectively form a structured output. Understanding multi-class classification provides a foundation to grasp these more complex outputs.
Digit Classification Example
To illustrate the concept of the training set, consider the digit classification problem. Images of handwritten digits are represented as matrices of pixel values, where each pixel value ranges from 0 to 1, with 0 representing a black pixel and 1 representing a white pixel. For a 28 by 28 pixel image, the matrix is flattened into a vector \(x\) in \(\mathbb{R}^{784}\) , where 784 is the product of the image dimensions. Each image corresponds to a high-dimensional vector, and the target value \(y\) is the actual digit the image represents, ranging from 0 to 9.
Language Modeling Example
In language modeling, the input can be a sentence, such as “The quick brown fox.” The target for this input could be the next word in the sequence, for example, “jumps.” Each word in the vocabulary is assigned a unique number. For example, the word “the” might be assigned the number 283, “quick” the number 78, “brown” the number 151 and so on. This numbering is arbitrary but must remain consistent across all inputs and examples within the model. The vocabulary size is defined, such as 1,000 possible words, and this set of words encompasses all the terms the language model needs to recognize.
One-hot encoding is used to represent words numerically. In this encoding, a word is represented by a vector that is mostly zeros except for a single one at the position corresponding to the word’s assigned number. For instance, if the vocabulary size is 1,000 words, and the word “the” is number 253, then the one-hot encoding for “the” would be a vector with a one at position 23 and zeros everywhere else.
The input to the model \(x\) , could be a vector contains the contatenation of some past history of words. If the model is designed to take three words as input for each prediction, and the vocabulary size is 1,000 words, then \(x\) would be a 3,000-dimensional vector. This vector would contain mostly zeros, with ones at the positions corresponding to the input words’ numbers. For example, if the input words are numbered 283, 78, and 151, then \(X_{283}\) , \(X_{1078}\) , and \(X_{2151}\) would be set to one, with all other positions in the vector set to zero.
The output of the model, denoted as \(Y\) , is not one-hot encoded but is simply the index number of the target word. If the target word is “fox” and it corresponds to index 723, then \(Y\) would be equal to 723.
Importance of Order
The order of words is crucial in language modeling. The input vector’s structure encodes the order of the words, with different segments of the vector representing the positions of the words in the input sequence. The concatenation of these segments ensures that the order is preserved, which is essential for the model to understand the meaning of sentences correctly.
In summary, language modeling involves assigning numbers to words, representing these words with one-hot encodings, and processing the input through a model that predicts the next word based on the numerical representation of the input sequence. The process of tokenization and the importance of maintaining the order of words are also highlighted as key components of language modeling.
Hypothesis Functions
In the context of machine learning, a hypothesis function, also referred to as a model, is a function that maps inputs to predictions. These predictions are made based on the input data, and if the hypothesis function is well-chosen, these predictions should be close to the actual targets. The formal representation of a hypothesis function is a function \[h : \mathbb{R}^n \rightarrow \mathbb{R}^k\] that maps inputs from \(\mathbb{R}^n\) to \(\mathbb{R}^k\) , where \(n\) is the dimensionality of the input space and \(k\) is the number of classes in a classification problem.
For multiclass classification, the output of the hypothesis function is a vector in \(\mathbb{R}^k\) , where each element of the vector represents a measure of belief for the corresponding class. This measure of belief is not necessarily a probability but indicates the relative confidence that the input belongs to each class. The \(j\) -th element of the vector \(h(x)\) , denoted as \(h(x)_j\) , corresponds to the belief that the input \(x\) is of class \(j\) . For example, if $ \[h(x) = \begin{bmatrix} -5.2 \\ 1.3 \\ 0.2 \end{bmatrix}\] this would suggest a low belief in class 1 and higher beliefs in classes 2 and 3. The class with the highest value in the vector is typically taken as the predicted class.
Parameterization of Hypothesis Functions
In practice, hypothesis functions are often parameterized by a set of parameters \(\theta\) , which is denoted \(h_\theta\) . These parameters define which specific hypothesis function from the hypothesis class is being used. The hypothesis class itself is a set of potential models from which the learning algorithm selects the most appropriate one based on the data. The choice of parameters \(\theta\) determines the behavior of the hypothesis function and its predictions.
Linear Hypothesis Class
A common example of a hypothesis class is the linear hypothesis class. In this class, the hypothesis function \(h_\theta(x)\) is defined as the matrix product of \(\theta\) and \(x\) , \[ h_\theta(x) = \theta^T x \] where \(\theta\) is a matrix of parameters and \(x\) is an input vector. The dimensions of \(\theta\) are determined by the dimensions of the input and output spaces. Specifically, for an input space of \(n\) dimensions and an output space of \(k\) dimensions, \(\theta\) must be a matrix of size \(n \times k\) to ensure the output is \(k\) -dimensional. Here, \(\theta\) is a matrix and the transpose operation \(\theta^T\) swaps its rows and columns. This function takes \(n\) -dimensional input vectors and produces \(k\) -dimensional output vectors, satisfying the requirements of the hypothesis class.
The parameters of a hypothesis function, often referred to as weights in machine learning terminology, define the specific instance of the function within the hypothesis class. These parameters are the elements of the matrix \(\theta\) in the case of a linear hypothesis class. The number of parameters, or weights, in a model can vary greatly depending on the complexity of the model. For instance, a neural network may have a large number of parameters, sometimes in the billions, which define the specific function it represents within its hypothesis class.
Understanding Matrix-Vector Products
To fully grasp the operation of a linear hypothesis function, one must be familiar with matrix-vector products. The product of a matrix \(\theta\) and a vector \(x\) results in a new vector, where each element is a linear combination of the elements of \(x\) weighted by the corresponding elements of \(\theta\) .
Efficacy of Linear Models
Linear models are surprisingly effective in many machine learning tasks. Despite their simplicity, they can achieve high accuracy in problems such as digit classification. The success of linear models raises questions about why they work well and under what circumstances more complex models might be necessary. These considerations will be explored further in subsequent discussions, along with practical examples and coding demonstrations.
Matrix Representation of Linear Hypothesis Functions
One can gain some insight into the performance of such a linear hypothesis function by looking more closely at the computations being performed. When the transposed matrix \(\theta^T\) is multiplied by the input vector \(x\) , the result is a \(k \times 1\) dimensional vector. This operation can be expressed as follows:
\[ \theta^T x = \begin{bmatrix} \theta_1^T \\ \theta_2^T \\ \vdots \\ \theta_k^T \end{bmatrix} x = \begin{bmatrix} \theta_1^T x \\ \theta_2^T x \\ \vdots \\ \theta_k^T x \end{bmatrix} \]
The \(i\) -th element of the resulting vector is the inner product of \(\theta_i^T\) and \(x\) , which can be written as:
\[ (\theta^T x)_i = \theta_i^T x = \sum_{j=1}^{n} \theta_{ij} x_j \]
This represents the sum of the products of the corresponding elements of the \(i\) -th row of \(\theta^T\) and the input vector \(x\) . Each element of the resulting vector is a scalar, as it is the product of a \(1 \times n\) matrix and an \(n \times 1\) matrix.
Template Matching in Linear Classification
The idea of template matches can help explain the effectiveness of such a model. Each \(\theta_i\) can be visualized as an image, where positive values indicate pixels that increase the likelihood of class \(i\) , and negative values indicate pixels that decrease it. When visualized, \(\theta_i\) resembles a template that matches the features of the corresponding digit. For example, \(\theta_1\) might have positive values where a digit ‘1’ typically has pixels and negative values around it, forming a template that matches the general shape of a ‘1’.
This template matching is a fundamental aspect of linear models in vision systems, where the weights in the model serve as generic templates for the classifier. The effectiveness of this approach is demonstrated by the fact that a linear classifier can achieve approximately 93% accuracy on a digit classification task, significantly better than random guessing, which would yield only 10% accuracy.
Batch/Minibatch Notation
In the context of machine learning, particularly for vision systems, inputs and targets are often represented in a batch or minibatch format. Inputs, denoted as \(x^{(i)}\) , are vectors in \(\mathbb{R}^n\) , where \(n\) is the dimension of the input. Targets, denoted as \(y^{(i)}\) , are elements in the set \(\{1, 2, \ldots, k\}\) , where \(k\) is the number of classes. These inputs and targets are typically organized into matrices for batch processing.
Inputs and Targets as Matrices
Inputs are defined as an \(m \times n\) matrix \(X\) , where \(m\) is the number of examples in the training set. Each row of \(X\) corresponds to an input vector transposed, such that the first row is \(x_1^T\) , the second row is \(x_2^T\) , and so on, up to \(x_m^T\) . The matrix \(X\) is expressed as:
\[ X = \begin{bmatrix} {x^{(1)}}^T \\ {x_{(2)}}^T \\ \vdots \\ {x_{(m)}}^T \end{bmatrix} \]
Targets are similarly organized into a vector \(Y\) , which is an \(m\) -dimensional vector containing the target values for each example in the training set. The vector \(Y\) is expressed as:
\[ Y = \begin{bmatrix} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(m)} \end{bmatrix} \]
The hypothesis function \(h_\theta\) can be also applied to an entire set of examples. When applied to a batch, the notation \(h_\theta(X)\) represents the application of \(h_\theta\) to every example within the batch. The result is a matrix where each row corresponds to the hypothesis function applied to the respective input vector. The expression for the hypothesis function applied to a batch is:
\[ h_{\theta}(X) = \begin{bmatrix} h_{\theta}(x^{(1)})^T \\ h_{\theta}(x^{(2)})^T \\ \vdots \\ h_{\theta}(x^{(m)})^T \end{bmatrix} \]
For a linear hypothesis function \(h_\theta(x) = \theta^T x\) , this takes a very simple form
\[ h_{\theta}(X) = \begin{bmatrix} (\theta^T x^{(1)} )^T \\ (\theta^T x^{(2)} )^T \\ \vdots \\ (\theta^T x^{(2)} )^T \end{bmatrix} = \begin{bmatrix} {x^{(1)}}^T \theta \\ {x^{(2)}}^T \theta \\ \vdots \\ {x^{(m)}}^T \theta \end{bmatrix} = X \theta \]
In other words, the hypothesis class applied to every example in the dataset has the extremely simple form of a single matrix operation \(X \theta\)
Implementation
We can implement all these operations very easily using libraries like PyTorch. Below is code that loads the MNIST dataset and computes a linear hypothesis function applied to all the data
Loss Functions
The second ingredient of a machine learning algorithm is the loss function. This function quantifies the difference between the predictions made by the classifier and the actual target labels. It formalizes the concept of a ‘good’ prediction by assigning a numerical value to the accuracy of the predictions. The loss function is a critical component of the training process, as it guides the optimization of the model parameters to improve the classifier’s performance.
Formal Definition of Loss Function
A loss function, denoted as \[ \ell : \mathbb{R}^k \times \{1,\ldots,k\} \] is a mapping from the output of hypothesis functions, which are vectors in \(\mathbb{R}^k\) for multiclass classification and true classes \(\{1, \ldots, k\}\) to positive real numbers. This mapping is applicable not only to multiclass classification but also has analogs for binary classification, regression, and other machine learning tasks.
Zero-One Loss Function
One of the most straightforward loss functions is the zero-one loss, also known as the error. This loss function is defined such that it equals zero if the prediction made by the classifier is correct and one otherwise. Formally, the zero-one loss function can be expressed as follows:
\[ \ell(h_\theta(x), y) = \begin{cases} 0 & \text{if } h_\theta(x)_y > h_\theta(x)_{y'} \text{ for all } y' \\ 1 & \text{otherwise} \end{cases} \]
This means that the loss is zero if the element with the highest value in the hypothesis output corresponds to the true class, indicating a correct prediction. Conversely, if any other element is higher, indicating an incorrect prediction, the loss is one.
Limitations of Zero-One Loss Function
Despite its intuitive appeal, the zero-one loss function is not ideal for two main reasons. Firstly, it is not differentiable, meaning it does not provide a smooth gradient that can guide the improvement of the classifier. This lack of differentiability means that the loss function does not offer a nuanced way to adjust the classifier’s parameters based on the degree of error in the predictions.
Secondly, the zero-one loss function does not handle the notion of stochastic or uncertain outputs well. In tasks like language modeling, where there is no single correct answer, the zero-one loss function fails to capture the probabilistic nature of the predictions. It assigns a hard loss value without considering the closeness of the prediction to the true class or the possibility of multiple plausible predictions.
Cross-Entropy Loss
The most commonly used loss function in modern machine learning is the cross-entropy loss. This loss function addresses the issue of transforming hypothesis outputs, which are often fuzzy and amorphous in terms of “belief,” into concrete probabilities. To achieve this, we introduce the softmax operator
Softmax Operator
To define cross-entropy loss, we need a mechanism to convert real-valued predictions to probabilities. This is achieved using the softmax function. Given a hypothesis function \(h\) that maps \(n\) -dimensional real-valued inputs to \(k\) -dimensional real-valued outputs (where \(k\) is the number of classes), the softmax function is defined as follows:
\[ \text{softmax}(h(x))_i = \frac{\exp(h(x)_i)}{\sum_{j=1}^{k} \exp(h(x)_j)} \]
This function ensures that the output is a probability distribution: each element is non-negative and the sum of all elements is 1.
Defining Cross-Entropy Loss
The goal of cross-entropy loss is to maximize the probability of the correct class. However, for practical and technical reasons, loss functions are typically minimized rather than maximized. Therefore, the negative log probability is used. The cross-entropy loss for a single prediction and the true class is defined as:
\[ \ell_{ce}(h(x), y) = -\log(\text{softmax}(h(x))_y) \]
This loss function takes the negative natural logarithm of the softmax probability corresponding to the true class \(y\) . The use of the logarithm helps to manage the scale of probability values, which can become very small or very large due to the exponential nature of the softmax function. While the initial intention might be to maximize the probability of the correct class, the cross-entropy loss is designed to be minimized. This is a common practice in optimization, where minimizing a loss function is equivalent to maximizing some form of likelihood or probability.
In the context of machine learning, the term “log” typically refers to the natural logarithm, sometimes denoted as \(\ln\) . However, for simplicity, the notation \(\log\) is used with the understanding that it implies the natural logarithm unless otherwise specified.
Simplification of Cross-Entropy Loss
The cross-entropy loss function can be simplified by examining the softmax function. The softmax function is defined as the exponential of a value over the sum of exponentials of a set of elements. When the logarithm of the softmax function is taken, due to the properties of logarithms, the expression simplifies to the difference between the log of the numerator and the log of the denominator. Since the numerator is an exponential function, and the logarithm is being applied to it, these operations cancel each other out, leaving the \(y\) th element of the hypothesis function \(h_{\theta}(x)\) .
The simplified expression for the first element of the cross-entropy loss, including the negation, is given by: \[ \ell_{ce}(h(x), y) = - h_{\theta}(x)_y + \log \sum_{j=1}^{k} \exp\left( h_{\theta}(x)_j \right) \] where \(k\) is the number of classes. The second term in the simplified cross-entropy loss expression involves the logarithm of a sum of exponentials, which is a non-simplifiable function known as the log-sum-exp function.
Vector Notation and Hadamard Product
To facilitate the computation, especially when taking derivatives, the cross-entropy loss can be expressed using vector notation. We specifically introduce the unit basis vector \(e_y\) , which is a one-hot vector with all elements being zero except for a one in the \(y\) th position. The cross-entropy loss can then be written as the inner product of \(E_y\) and the hypothesis function \(h_{\beta}(x)\) , negated: \[ \ell_{ce}(h(x), y) = -e_y^T h_{\theta}(x) + \log \sum_{j=1}^{K} \exp\left( h_{\theta}(x)_j \right) \]
Batch Form of Loss Function
The loss function can also be expressed in batch form, which is useful for processing multiple examples simultaneously. The batch loss is defined as the average of the individual losses over all examples in the batch. Let \(X \in \mathbb{R}^{M \times N}\) be the matrix of input features for all examples in the batch, and \(Y\) be the corresponding vector of labels. The batch loss is given by: \[ \ell_{ce}(h_{\beta}(X), Y) = \frac{1}{m} \sum_{i=1}^{m} \ell_{ce}(h_{\theta}(x^{(i)}), y^{(i)}) \] where \(\ell_{ce}\) is the cross-entropy loss for a single example, \(,\) is the number of examples in the batch, and \(x^{(i)}\) and \(y^{(i)}\) are the \(i\) th example and target, respectively.
Implementing both the zero-one loss and the cross entropy loss in Python is straightforward.
Zero-one loss
The zero-one loss is a simple loss function that counts the number of misclassifications. It is defined as zero if the predicted class (the class with largest value of the hypothesis function) for an example matches the actual class, and one otherwise. To compute the 0-1 loss in Python, the argmax function is used to identify the column that achieves the maximum value for each sample. The argmax function takes an argument specifying the dimension over which to perform the operation. Using -1 as the argument indicates that the operation should be performed over the last dimension, yielding a list of indices corresponding to the maximum values in each row of the tensor. The matrix \(H\) represents the hypothesis function applied to the input matrix \(X\) , and vector \(Y\) contains the actual class labels for each example.
The cross-entropy loss function is more complex than the 0-1 loss but can also be implemented concisely in Python. To compute the first term of the cross entropy loss, we simply index intro the \(y\) th element for each row of \(H\) . The second term, the log-sum-exp, is computed by exponentiating the hypothesis matrix \(H\) , summing over the last dimension (each row), and then taking the logarithm of the result. This term accounts for the normalization of the predicted probabilities and is summed over all samples to complete the cross-entropy loss calculation.
An example is provided where the cross-entropy loss is calculated between a prediction \(H\) and the true labels \(Y\) , resulting in a high loss value of 15. This high value is indicative of the fact that when predictions are incorrect, they can be significantly off, which is captured by the cross-entropy loss. A comparison is made to a scenario where the predictions are all zeros, which would result in a lower cross-entropy loss, highlighting the sensitivity of this loss function to the probabilities associated with the true class labels.
Optimization
The final ingredient of machine learning is the optimization method. Specifically, the goal of the machine learning optimization problem is to find the set of paramaters that minimizes the average loss of the corresponding hypothesis function and target output, over the entire training set. This is written as finding the set of parameters \(\theta\) that minimizes the average loss over the entire training set:
\[ \DeclareMathOperator{\minimize}{minimize} \minimize_{\theta} \frac{1}{m} \sum_{i=1}^{m} \ell(h_{\theta}(x^{(i)}), y^{(i)}) \]
This optimization problem is at the core of all machine learning algorithms, regardless of the specific type, such as neural networks, linear regression, or boosted decision trees. The goal is to search among the class of allowable functions determined by the parameters \(\theta\) to find the one that best fits the training data according to the chosen loss function.
While the lecture will initially focus on the manual computation of derivatives, modern libraries like PyTorch offer automatic differentiation, which eliminates the need for manual derivative calculations. However, understanding the underlying process is valuable. The course will later cover automatic differentiation at a high level, and after some initial manual calculations, we will rely on PyTorch to handle derivatives.
For linear classification problems utilizing cross-entropy loss, the optimization problem is formalized as minimizing the average cross-entropy loss over all training examples. This is given by
\[ \minimize_{\theta} \frac{1}{m} \sum_{i=1}^{m} \ell_{ce}(x^{(i)}), y^{(i)}) \] where \(\theta\) represents the parameters of the linear classifier.
Gradient Descent
The gradient descent algorithm is an iterative method to find the parameters that minimize the loss function. The process involves taking small steps in the direction opposite to the gradient (a multivariate analog of the derivate derivative) of the loss function at the current point.
An analogous update rule for the parameters in the one-dimensional case is given by: \[ x_{n+1} = x_n - \alpha \cdot f'(x_n) \] where \(x_n\) is some current parameter value, \(\alpha\) is the step size (also known as the learning rate), and \(f'(x_n)\) is the derivative of the loss function with respect to the parameter at \(x_n\) .
The derivative provides the direction of the steepest ascent, and by moving in the opposite direction (negative derivative), the algorithm seeks to reduce the loss function value, moving towards a local minimum.
The Gradient
The gradient is a generalization of the derivative for functions with multivariate inputs, such as vectors or matrices. It is a matrix of partial derivatives and is denoted as \(\nabla f(\theta)\) , where \(\theta\) is the point at which the gradient is evaluated. The gradient is only defined for functions with scalar-valued outputs.
For a function \(f: \mathbb{R}^{n \times k} \rightarrow \mathbb{R}\) , the gradient \(\nabla_\theta f(\theta)\) is an \(n \times k\) matrix given by:
\[ \nabla_\theta f(\theta) = \begin{bmatrix} \frac{\partial f(\theta)}{\partial \theta_{11}} & \cdots & \frac{\partial f(\theta)}{\partial \theta_{1k}} \\ \vdots & \ddots & \vdots \\ \frac{\partial f(\theta)}{\partial \theta_{n1}} & \cdots & \frac{\partial f(\theta)}{\partial \theta_{nk}} \end{bmatrix} \]
Each element of this matrix is the partial derivative of \(f\) with respect to the corresponding element of \(\theta\) . A partial derivative is computed by treating all other elements of \(\theta\) as constants.
The gradient has a crucial property that it always points in the direction of the steepest ascent in the function’s value. Conversely, the negative gradient points in the direction of the steepest descent, which is useful for optimization. This property holds true for functions with vector or matrix inputs, just as the derivative points in the direction of steepest ascent for functions with a single input. This concept is fundamental as it implies that by evaluating the gradient, one can determine the direction that is most uphill or, conversely, most downhill by considering the negative gradient. This property is crucial in machine learning because it allows for scanning every possible direction around a current point to find the single direction that points most uphill or downhill.
Gradient Descent: The Core Algorithm
Gradient descent is highlighted as one of the single most important algorithms in computer science, particularly in the field of artificial intelligence. It is the underlying algorithm for training various AI models and is used in almost every advance in AI. Gradient descent is a procedure for iteratively minimizing a function, and it consists of the following steps:
- Initialization : Begin with an initial point \(\theta\) .
- Iteration : For a predetermined number of iterations \(T\) , repeat the following update: \[ \theta := \theta - \alpha \nabla_\theta f(\theta) \] where \(\alpha\) is a positive real value known as the step size, and \(\nabla_\theta f(\theta)\) is the gradient of the function \(f\) with respect to \(\theta\) evaluated at the current point \(\theta\) .
The function \(f\) is the one to be optimized, and the choice of step size \(\alpha\) and the number of iterations \(T\) can significantly affect the optimization process. Libraries such as PyTorch can compute gradients automatically using a technique called automatic differentiation, simplifying the optimization process even further.
Practical Considerations and Variants
While the basic premise of gradient descent is straightforward, practical implementation involves several considerations. The choice of step size is critical, and the number of iterations must be chosen carefully to ensure convergence. In the context of neural networks, initialization plays a significant role, although it is less critical for convex problems.
Stochastic Gradient Descent (SGD)
Stochastic Gradient Descent (SGD) is a variant of the gradient descent algorithm, particularly useful when the objective function is an average of many individual functions. This is often the case in machine learning, where the objective is to minimize the average loss across a dataset.
For example, consider the applciation of SGD to multi-class linear classification. The objective function in such cases is typically the sum or average of loss functions over the training examples:
\[ \min_{\theta} \frac{1}{m} \sum_{i=1}^{m} \ell(h_{\theta}(x^{(i)}), y^{(i)}) \]
where \(\ell\) is the loss function, \(h_{\theta}\) is the hypothesis function parameterized by \(\theta\) , \(x^{(i)}\) is the \(i\) -th training example, and \(y^{(i)}\) is the corresponding target value.
Batch Processing in SGD
Instead of computing the gradient over the entire dataset, which can be computationally expensive, SGD approximates the gradient using a random subset of the data, known as a batch or minibatch. The size of the batch, denoted by \(|B|\) , is typically much smaller than the size of the full dataset, allowing for more frequent updates of the parameters within the same computational budget. The approximation of the objective function using a batch is given by: \[ \frac{1}{|B|} \sum_{i \in B} \ell(h_{\theta}(x^{(i)}), y^{(i)}) \] where \(B\) is a randomly selected subset of the indices from \(1\) to \(m\) . This subset is used to compute the gradient and update the parameters.
Algorithmic Description of SGD
The SGD algorithm proceeds by initializing the parameters and then iteratively updating them by subtracting a scaled gradient computed on a random batch. The scaling factor is often referred to as the learning rate. The algorithm can be summarized as follows:
- Initialize \(\theta\) .
- Select a random batch $B {1,,m}.
- Update \(\theta\) by subtracting a fraction of the gradient. \[ \theta := \theta - \frac{\alpha}{|B|} \sum_{i\in B} \nabla_\theta \ell(h_{\theta}(x^{(i)}), y^{(i)})\]
We emphasize that while the intermediate steps of deriving gradients may appear complex, the process is manageable and will eventually be simplified by using automatic differentiation tools. However, understanding the mechanics of SGD is important for grasping the underlying principles of optimization in machine learning.
In practice, rather than selecting a completely random subset each time, the dataset is often divided into batches of a fixed size, and the algorithm iterates over these batches. This approach is known as mini-batch gradient descent. The size of the mini-batch is a trade-off between computational efficiency and the frequency of updates. While a batch size of one (pure SGD) maximizes the number of updates, it is not computationally efficient due to the reliance on matrix-vector products rather than matrix-matrix products. Common batch sizes are 32 or 64, which balance the speed of updates with computational efficiency.
Cyclic SGD is a variant where the entire dataset is iterated over in chunks or batches, possibly in a randomized order. This method is harder to analyze mathematically compared to the true form of SGD, where a new random subset is selected at each iteration. However, cyclic SGD is a reasonable approximation used in practice.
Computational Trade-offs
The choice of batch size in SGD is influenced by the trade-off between the accuracy of the gradient direction and the speed of computation. Smaller batch sizes allow for more frequent updates but may provide a rougher approximation of the true gradient. Conversely, larger batch sizes use computational resources more efficiently but update the parameters less frequently. The optimal batch size depends on the specific problem and computational constraints.
Computing the Stochastic Gradient Descent Updates
To perform SGD updates, we need to compute the gradient of the loss function with respect to the parameters. In the context of multi-class linear classification, the loss function is the cross-entropy loss of the hypothesis class, which is a linear function of the parameters \(\beta\) and the input features \(x\) . The cross-entropy loss can be expressed as:
\[ \ell(\theta^T x, y) = -e_y^T (\theta^T x) + \log \left( \sum_{j=1}^{k} e^{\theta_j^T x} \right) \]
where \(e_y\) is the basis vector corresponding to the true class, \(\theta\) is the parameter matrix, and \(k\) is the number of classes. The \(j\) -th column of \(\theta\) , denoted as \(\theta_j\) , represents the parameters corresponding to the \(j\) -th class.
Elementwise computation of the Gradient
The gradient of the loss function with respect to \(\theta\) is a matrix of partial derivatives. To compute this gradient, we can consider each element of the matrix, which involves taking the partial derivative with respect to each element \(\theta_{rs}\) of the parameter matrix \(\theta\) . The gradient with respect to \(\theta_{rs}\) of the loss function is given by: \[ \frac{\partial}{\partial \theta_{rs}} -e_y^T (\theta^T x) = -x_r \cdot \mathbb{1}_{\{s=y\}} \] where \(\mathbb{1}(y = s)\) is the indicator function that is 1 if the true class label \(y\) \(s\) and 0 otherwise, and \(x_r\) is the \(r\) -th feature of the \(x\) .
Next we consider the partial derivative of the log-sum-exp term. The derivative of the log of a function is the derivative of the function divided by the function itself. Applying this to the softmax function, the derivative with respect to \(\theta_{rs}\) is computed as follows:
\[ \begin{align} \frac{\partial}{\partial \theta_{rs}} \log \left( \sum_{j=1}^{K} \exp \left( \sum_{i=1}^{N} \theta_{ij} X_i \right) \right) & = \frac{\frac{\partial}{\partial \theta_{rs}} \left( \sum_{j=1}^{K} \exp \left( \sum_{i=1}^{N} \theta_{ij} x_i \right) \right)}{ \sum_{j=1}^{K} \exp \left( \sum_{i=1}^{N} \theta_{ij} X_i \right) } \\ & = \frac{\exp \left( \sum_{i=1}^{N} \theta_{is} x_i \right) \cdot x_r}{ \sum_{j=1}^{K} \exp \left( \sum_{i=1}^{N} \theta_{ij} X_i \right) } \end{align} \]
Gradient in Native Matrix Form
The gradient of a function with respect to its parameters can be expressed in a native matrix form. This form simplifies the representation and calculation of the gradient. Looking at the expression for the \(rs\) element of the gradient, we can respresent all elements of the gradient simultaneously as \[ \nabla_\theta \ell_{ce}(\theta^T x, y) = -x (\mathbf{e}_y - \text{softmax}(\theta^T x))^T. \]
Thus, the gradient of the loss for a given example is the product of the example vector \(\mathbf{x}\) and the difference between the probabilistic prediction and the one-hot vector of the targets. This form of the gradient is intuitive as it adjusts the parameters corresponding to the weights of the matrix to minimize the difference between the predicted probabilities and the actual target distribution.
Secret of Vector Calculus
Although we can always derive gradients element-by-element in this manner, there is a way that is easier in practice, and works well for most practical cases. The core idea is to treat all the elements in an expression as scalars, compute the derivates using normal scalar calculus, and then determine the gradient form by matching sizes. This may not always work, but it often in fact gives the correct gradient. To see how this works, we can first define the cross entropy loss of a linear classifier in a “vector” form \[ \ell_{ce}(\theta^T x,y) = -e_y^T \theta^T x + \log(\mathbf{1}^T \exp(\theta^T x)) \] where \(\mathbf{1}\) represents the vector of all ones. Now taking the derivative with respect to \(\theta\) , assuming that all values are scalars, and applying the chain rule we have \[ \frac{\partial}{\partial \theta} \ell_{ce}(\theta^T x,y) = -e_y x + \frac{\exp(\theta^T x) x}{1^T \exp(\theta^T x)} = x (-e_y^T + \text{softmax}(\theta^T x)). \] Re-arranging terms so that the sizes match, we have as above that \[ \nabla_\theta \ell_{ce}(\theta^T x, y) = -x (\mathbf{e}_y - \text{softmax}(\theta^T x))^T. \]
Batch Gradient Computation
This gradient has be easily extended to a batch of examples. The loss function is overloaded to handle batches, and the derivative with respect to \(\theta\) for the entire batch is computed. The batch version of the hypothesis function is represented by the matrix product \(X\theta\) , where \(X\) is the matrix of input features for the entire batch. The derivative for the batch is given by: \[ \frac{\partial}{\partial \theta} \ell_{ce}(X\theta, Y) = X^T \left(-I_y + \text{softmax}(X\theta)\right) \] where \(I_Y\) is the matrix of one-hot encoded targets in each row for the entire batch, and \(\text{softmax}(X\theta)\) is the softmax function applied to each row of the matrix product \(X\theta\) . The resulting gradient is an \(n \times k\) dimensional matrix, where \(n\) is the number of features and \(k\) is the number of classes.
Numerical Gradient Approximation
To verify the correctness of the derived gradient expression, a numerical gradient approximation method is introduced. This method involves perturbing each element of the parameter matrix \(\theta\) by a small value \(\epsilon\) and computing the resulting change in the cross-entropy loss. This can be computed using the following code:
The numerical gradient approximation serves as a check against the analytically derived gradient. If the numerical and analytical gradients match for a randomly initialized \(\theta\) , it is likely that the analytical gradient is correct. However, it is cautioned that this method can be computationally expensive, as it requires iterating over every element of \(\theta\) and evaluating the loss function multiple times. Thus, it’s only used as a measure to check the analytical gradient, and then you would want to use the analytical computation of the gradient after that.
Implementation in PyTorch
Let’s put all these elements together to implement a complete implementation of linear class classification in Python. While the resulting code is quite small, it’s important to emphasize the complexity of what is happening. Specifically, the implementation defines all the three ingredients of a machine learning algorithm: 1. We use a linear hypothesis function \(h_\theta(x) = \theta^T x\) 2. We use the cross entropy loss \(\ell_{ce}(h_\theta(x), y)\) 3. We solve the optimization problem of finding the parameters that minimize the loss over the training set using stochastic gradient descent updates by via the updates \[ \theta := \theta - \frac{\alpha}{|B|} \cdot X^T(\text{softmax}(X\theta) - I_Y) \]
Running this example on the MNIST dataset results in a linear classifier that achieves about 7.5% error, on a held out test set. We can further try to visualize the results columns of theta and the results look approximately like “templates” for the digits we are trying to classify. Generally speaking, such visualization won’t be possible for more complex classifiers, but this kind of “template matching” nonetheless provides a reasonable intuition about what machine learning methods are doing, even for more complex classifiers.
- Comprehensive Learning Paths
- 150+ Hours of Videos
- Complete Access to Jupyter notebooks, Datasets, References.

Hypothesis Testing – A Deep Dive into Hypothesis Testing, The Backbone of Statistical Inference
- September 21, 2023
Explore the intricacies of hypothesis testing, a cornerstone of statistical analysis. Dive into methods, interpretations, and applications for making data-driven decisions.

In this Blog post we will learn:
- What is Hypothesis Testing?
- Steps in Hypothesis Testing 2.1. Set up Hypotheses: Null and Alternative 2.2. Choose a Significance Level (α) 2.3. Calculate a test statistic and P-Value 2.4. Make a Decision
- Example : Testing a new drug.
- Example in python
1. What is Hypothesis Testing?
In simple terms, hypothesis testing is a method used to make decisions or inferences about population parameters based on sample data. Imagine being handed a dice and asked if it’s biased. By rolling it a few times and analyzing the outcomes, you’d be engaging in the essence of hypothesis testing.
Think of hypothesis testing as the scientific method of the statistics world. Suppose you hear claims like “This new drug works wonders!” or “Our new website design boosts sales.” How do you know if these statements hold water? Enter hypothesis testing.
2. Steps in Hypothesis Testing
- Set up Hypotheses : Begin with a null hypothesis (H0) and an alternative hypothesis (Ha).
- Choose a Significance Level (α) : Typically 0.05, this is the probability of rejecting the null hypothesis when it’s actually true. Think of it as the chance of accusing an innocent person.
- Calculate Test statistic and P-Value : Gather evidence (data) and calculate a test statistic.
- p-value : This is the probability of observing the data, given that the null hypothesis is true. A small p-value (typically ≤ 0.05) suggests the data is inconsistent with the null hypothesis.
- Decision Rule : If the p-value is less than or equal to α, you reject the null hypothesis in favor of the alternative.
2.1. Set up Hypotheses: Null and Alternative
Before diving into testing, we must formulate hypotheses. The null hypothesis (H0) represents the default assumption, while the alternative hypothesis (H1) challenges it.
For instance, in drug testing, H0 : “The new drug is no better than the existing one,” H1 : “The new drug is superior .”
2.2. Choose a Significance Level (α)
When You collect and analyze data to test H0 and H1 hypotheses. Based on your analysis, you decide whether to reject the null hypothesis in favor of the alternative, or fail to reject / Accept the null hypothesis.
The significance level, often denoted by $α$, represents the probability of rejecting the null hypothesis when it is actually true.
In other words, it’s the risk you’re willing to take of making a Type I error (false positive).
Type I Error (False Positive) :
- Symbolized by the Greek letter alpha (α).
- Occurs when you incorrectly reject a true null hypothesis . In other words, you conclude that there is an effect or difference when, in reality, there isn’t.
- The probability of making a Type I error is denoted by the significance level of a test. Commonly, tests are conducted at the 0.05 significance level , which means there’s a 5% chance of making a Type I error .
- Commonly used significance levels are 0.01, 0.05, and 0.10, but the choice depends on the context of the study and the level of risk one is willing to accept.
Example : If a drug is not effective (truth), but a clinical trial incorrectly concludes that it is effective (based on the sample data), then a Type I error has occurred.
Type II Error (False Negative) :
- Symbolized by the Greek letter beta (β).
- Occurs when you accept a false null hypothesis . This means you conclude there is no effect or difference when, in reality, there is.
- The probability of making a Type II error is denoted by β. The power of a test (1 – β) represents the probability of correctly rejecting a false null hypothesis.
Example : If a drug is effective (truth), but a clinical trial incorrectly concludes that it is not effective (based on the sample data), then a Type II error has occurred.
Balancing the Errors :

In practice, there’s a trade-off between Type I and Type II errors. Reducing the risk of one typically increases the risk of the other. For example, if you want to decrease the probability of a Type I error (by setting a lower significance level), you might increase the probability of a Type II error unless you compensate by collecting more data or making other adjustments.
It’s essential to understand the consequences of both types of errors in any given context. In some situations, a Type I error might be more severe, while in others, a Type II error might be of greater concern. This understanding guides researchers in designing their experiments and choosing appropriate significance levels.
2.3. Calculate a test statistic and P-Value
Test statistic : A test statistic is a single number that helps us understand how far our sample data is from what we’d expect under a null hypothesis (a basic assumption we’re trying to test against). Generally, the larger the test statistic, the more evidence we have against our null hypothesis. It helps us decide whether the differences we observe in our data are due to random chance or if there’s an actual effect.
P-value : The P-value tells us how likely we would get our observed results (or something more extreme) if the null hypothesis were true. It’s a value between 0 and 1. – A smaller P-value (typically below 0.05) means that the observation is rare under the null hypothesis, so we might reject the null hypothesis. – A larger P-value suggests that what we observed could easily happen by random chance, so we might not reject the null hypothesis.
2.4. Make a Decision
Relationship between $α$ and P-Value
When conducting a hypothesis test:
We then calculate the p-value from our sample data and the test statistic.
Finally, we compare the p-value to our chosen $α$:
- If $p−value≤α$: We reject the null hypothesis in favor of the alternative hypothesis. The result is said to be statistically significant.
- If $p−value>α$: We fail to reject the null hypothesis. There isn’t enough statistical evidence to support the alternative hypothesis.
3. Example : Testing a new drug.
Imagine we are investigating whether a new drug is effective at treating headaches faster than drug B.
Setting Up the Experiment : You gather 100 people who suffer from headaches. Half of them (50 people) are given the new drug (let’s call this the ‘Drug Group’), and the other half are given a sugar pill, which doesn’t contain any medication.
- Set up Hypotheses : Before starting, you make a prediction:
- Null Hypothesis (H0): The new drug has no effect. Any difference in healing time between the two groups is just due to random chance.
- Alternative Hypothesis (H1): The new drug does have an effect. The difference in healing time between the two groups is significant and not just by chance.
Calculate Test statistic and P-Value : After the experiment, you analyze the data. The “test statistic” is a number that helps you understand the difference between the two groups in terms of standard units.
For instance, let’s say:
- The average healing time in the Drug Group is 2 hours.
- The average healing time in the Placebo Group is 3 hours.
The test statistic helps you understand how significant this 1-hour difference is. If the groups are large and the spread of healing times in each group is small, then this difference might be significant. But if there’s a huge variation in healing times, the 1-hour difference might not be so special.
Imagine the P-value as answering this question: “If the new drug had NO real effect, what’s the probability that I’d see a difference as extreme (or more extreme) as the one I found, just by random chance?”
For instance:
- P-value of 0.01 means there’s a 1% chance that the observed difference (or a more extreme difference) would occur if the drug had no effect. That’s pretty rare, so we might consider the drug effective.
- P-value of 0.5 means there’s a 50% chance you’d see this difference just by chance. That’s pretty high, so we might not be convinced the drug is doing much.
- If the P-value is less than ($α$) 0.05: the results are “statistically significant,” and they might reject the null hypothesis , believing the new drug has an effect.
- If the P-value is greater than ($α$) 0.05: the results are not statistically significant, and they don’t reject the null hypothesis , remaining unsure if the drug has a genuine effect.
4. Example in python
For simplicity, let’s say we’re using a t-test (common for comparing means). Let’s dive into Python:
Making a Decision : “The results are statistically significant! p-value < 0.05 , The drug seems to have an effect!” If not, we’d say, “Looks like the drug isn’t as miraculous as we thought.”
5. Conclusion
Hypothesis testing is an indispensable tool in data science, allowing us to make data-driven decisions with confidence. By understanding its principles, conducting tests properly, and considering real-world applications, you can harness the power of hypothesis testing to unlock valuable insights from your data.
More Articles
Correlation – connecting the dots, the role of correlation in data analysis, sampling and sampling distributions – a comprehensive guide on sampling and sampling distributions, law of large numbers – a deep dive into the world of statistics, central limit theorem – a deep dive into central limit theorem and its significance in statistics, skewness and kurtosis – peaks and tails, understanding data through skewness and kurtosis”, similar articles, complete introduction to linear regression in r, how to implement common statistical significance tests and find the p value, logistic regression – a complete tutorial with examples in r.
Subscribe to Machine Learning Plus for high value data science content
© Machinelearningplus. All rights reserved.

Machine Learning A-Z™: Hands-On Python & R In Data Science
Free sample videos:.


Best Guesses: Understanding The Hypothesis in Machine Learning
- February 22, 2024
- General , Supervised Learning , Unsupervised Learning
Machine learning is a vast and complex field that has inherited many terms from other places all over the mathematical domain.
It can sometimes be challenging to get your head around all the different terminologies, never mind trying to understand how everything comes together.
In this blog post, we will focus on one particular concept: the hypothesis.
While you may think this is simple, there is a little caveat regarding machine learning.
The statistics side and the learning side.
Don’t worry; we’ll do a full breakdown below.
You’ll learn the following:
What Is a Hypothesis in Machine Learning?
- Is This any different than the hypothesis in statistics?
- What is the difference between the alternative hypothesis and the null?
- Why do we restrict hypothesis space in artificial intelligence?
- Example code performing hypothesis testing in machine learning

In machine learning, the term ‘hypothesis’ can refer to two things.
First, it can refer to the hypothesis space, the set of all possible training examples that could be used to predict or answer a new instance.
Second, it can refer to the traditional null and alternative hypotheses from statistics.
Since machine learning works so closely with statistics, 90% of the time, when someone is referencing the hypothesis, they’re referencing hypothesis tests from statistics.
Is This Any Different Than The Hypothesis In Statistics?
In statistics, the hypothesis is an assumption made about a population parameter.
The statistician’s goal is to prove it true or disprove it.

This will take the form of two different hypotheses, one called the null, and one called the alternative.
Usually, you’ll establish your null hypothesis as an assumption that it equals some value.
For example, in Welch’s T-Test Of Unequal Variance, our null hypothesis is that the two means we are testing (population parameter) are equal.
This means our null hypothesis is that the two population means are the same.
We run our statistical tests, and if our p-value is significant (very low), we reject the null hypothesis.
This would mean that their population means are unequal for the two samples you are testing.
Usually, statisticians will use the significance level of .05 (a 5% risk of being wrong) when deciding what to use as the p-value cut-off.
What Is The Difference Between The Alternative Hypothesis And The Null?
The null hypothesis is our default assumption, which we are trying to prove correct.
The alternate hypothesis is usually the opposite of our null and is much broader in scope.
For most statistical tests, the null and alternative hypotheses are already defined.
You are then just trying to find “significant” evidence we can use to reject our null hypothesis.

These two hypotheses are easy to spot by their specific notation. The null hypothesis is usually denoted by H₀, while H₁ denotes the alternative hypothesis.
Example Code Performing Hypothesis Testing In Machine Learning
Since there are many different hypothesis tests in machine learning and data science, we will focus on one of my favorites.
This test is Welch’s T-Test Of Unequal Variance, where we are trying to determine if the population means of these two samples are different.
There are a couple of assumptions for this test, but we will ignore those for now and show the code.
You can read more about this here in our other post, Welch’s T-Test of Unequal Variance .
We see that our p-value is very low, and we reject the null hypothesis.

What Is The Difference Between The Biased And Unbiased Hypothesis Spaces?
The difference between the Biased and Unbiased hypothesis space is the number of possible training examples your algorithm has to predict.
The unbiased space has all of them, and the biased space only has the training examples you’ve supplied.
Since neither of these is optimal (one is too small, one is much too big), your algorithm creates generalized rules (inductive learning) to be able to handle examples it hasn’t seen before.
Here’s an example of each:
Example of The Biased Hypothesis Space In Machine Learning
The Biased Hypothesis space in machine learning is a biased subspace where your algorithm does not consider all training examples to make predictions.
This is easiest to see with an example.
Let’s say you have the following data:
Happy and Sunny and Stomach Full = True
Whenever your algorithm sees those three together in the biased hypothesis space, it’ll automatically default to true.
This means when your algorithm sees:
Sad and Sunny And Stomach Full = False
It’ll automatically default to False since it didn’t appear in our subspace.
This is a greedy approach, but it has some practical applications.

Example of the Unbiased Hypothesis Space In Machine Learning
The unbiased hypothesis space is a space where all combinations are stored.
We can use re-use our example above:
This would start to breakdown as
Happy = True
Happy and Sunny = True
Happy and Stomach Full = True
Let’s say you have four options for each of the three choices.
This would mean our subspace would need 2^12 instances (4096) just for our little three-word problem.
This is practically impossible; the space would become huge.

So while it would be highly accurate, this has no scalability.
More reading on this idea can be found in our post, Inductive Bias In Machine Learning .
Why Do We Restrict Hypothesis Space In Artificial Intelligence?
We have to restrict the hypothesis space in machine learning. Without any restrictions, our domain becomes much too large, and we lose any form of scalability.
This is why our algorithm creates rules to handle examples that are seen in production.
This gives our algorithms a generalized approach that will be able to handle all new examples that are in the same format.
Other Quick Machine Learning Tutorials
At EML, we have a ton of cool data science tutorials that break things down so anyone can understand them.
Below we’ve listed a few that are similar to this guide:
- Instance-Based Learning in Machine Learning
- Types of Data For Machine Learning
- Verbose in Machine Learning
- Generalization In Machine Learning
- Epoch In Machine Learning
- Inductive Bias in Machine Learning
- Understanding The Hypothesis In Machine Learning
- Zip Codes In Machine Learning
- get_dummies() in Machine Learning
- Bootstrapping In Machine Learning
- X and Y in Machine Learning
- F1 Score in Machine Learning
- Recent Posts
- Python for Data Science: Applications & Impact Unveiled [Must-Read] - July 18, 2024
- Boost Customer Service in the Workplace [Unleash Your Team’s Potential] - July 18, 2024
- What Computer Software Do Veterinarians Use? [Discover the Best Tools Here] - July 17, 2024
Hypothesis in Machine Learning: Comprehensive Overview(2021)
Introduction
Supervised machine learning (ML) is regularly portrayed as the issue of approximating an objective capacity that maps inputs to outputs. This portrayal is described as looking through and assessing competitor hypothesis from hypothesis spaces.
The conversation of hypothesis in machine learning can be confused for a novice, particularly when “hypothesis” has a discrete, but correlated significance in statistics and all the more comprehensively in science.
Hypothesis Space (H)
The hypothesis space utilized by an ML system is the arrangement of all hypotheses that may be returned by it. It is ordinarily characterized by a Hypothesis Language, conceivably related to a Language Bias.
Many ML algorithms depend on some sort of search methodology: given a set of perceptions and a space of all potential hypotheses that may be thought in the hypothesis space. They see in this space for those hypotheses that adequately furnish the data or are ideal concerning some other quality standard.
ML can be portrayed as the need to utilize accessible data objects to discover a function that most reliable maps inputs to output, alluded to as function estimate, where we surmised an anonymous objective function that can most reliably map inputs to outputs on all expected perceptions from the difficult domain. An illustration of a model that approximates the performs mappings and target function of inputs to outputs is known as hypothesis testing in machine learning.
The hypothesis in machine learning of all potential hypothesis that you are looking over, paying little mind to their structure. For the wellbeing of accommodation, the hypothesis class is normally compelled to be just each sort of function or model in turn, since learning techniques regularly just work on each type at a time. This doesn’t need to be the situation, however:
- Hypothesis classes don’t need to comprise just one kind of function. If you’re looking through exponential, quadratic, and overall linear functions, those are what your joined hypothesis class contains.
- Hypothesis classes additionally don’t need to comprise of just straightforward functions. If you figure out how to look over all piecewise-tanh2 functions, those functions are what your hypothesis class incorporates.
The enormous trade-off is that the bigger your hypothesis class in machine learning, the better the best hypothesis models the basic genuine function, yet the harder it is to locate that best hypothesis. This is identified with the bias-variance trade-off.
- Hypothesis (h)
A hypothesis function in machine learning is best describes the target. The hypothesis that an algorithm would concoct relies on the data and relies on the bias and restrictions that we have forced on the data.
The hypothesis formula in machine learning:
- y is range
- m changes in y divided by change in x
- x is domain
- b is intercept
The purpose of restricting hypothesis space in machine learning is so that these can fit well with the general data that is needed by the user. It checks the reality or deception of observations or inputs and examinations them appropriately. Subsequently, it is extremely helpful and it plays out the valuable function of mapping all the inputs till they come out as outputs. Consequently, the target functions are deliberately examined and restricted dependent on the outcomes (regardless of whether they are free of bias), in ML.
The hypothesis in machine learning space and inductive bias in machine learning is that the hypothesis space is a collection of valid Hypothesis, for example, every single desirable function, on the opposite side the inductive bias (otherwise called learning bias) of a learning algorithm is the series of expectations that the learner uses to foresee outputs of given sources of inputs that it has not experienced. Regression and Classification are a kind of realizing which relies upon continuous-valued and discrete-valued sequentially. This sort of issues (learnings) is called inductive learning issues since we distinguish a function by inducting it on data.
In the Maximum a Posteriori or MAP hypothesis in machine learning, enhancement gives a Bayesian probability structure to fitting model parameters to training data and another option and sibling may be a more normal Maximum Likelihood Estimation system. MAP learning chooses a solitary in all probability theory given the data. The hypothesis in machine learning earlier is as yet utilized and the technique is regularly more manageable than full Bayesian learning.
Bayesian techniques can be utilized to decide the most plausible hypothesis in machine learning given the data the MAP hypothesis. This is the ideal hypothesis as no other hypothesis is more probable.
Hypothesis in machine learning or ML the applicant model that approximates a target function for mapping instances of inputs to outputs.
Hypothesis in statistics probabilistic clarification about the presence of a connection between observations.
Hypothesis in science is a temporary clarification that fits the proof and can be disproved or confirmed. We can see that a hypothesis in machine learning draws upon the meaning of the hypothesis all the more extensively in science.
There are no right or wrong ways of learning AI and ML technologies – the more, the better! These valuable resources can be the starting point for your journey on how to learn Artificial Intelligence and Machine Learning. Do pursuing AI and ML interest you? If you want to step into the world of emerging tech, you can accelerate your career with this Machine Learning And AI Courses by Jigsaw Academy.
- XGBoost Algorithm: An Easy Overview For 2021
Fill in the details to know more
PEOPLE ALSO READ

Related Articles

From The Eyes Of Emerging Technologies: IPL Through The Ages
April 29, 2023
Personalized Teaching with AI: Revolutionizing Traditional Teaching Methods
April 28, 2023
Metaverse: The Virtual Universe and its impact on the World of Finance
April 13, 2023
Artificial Intelligence – Learning To Manage The Mind Created By The Human Mind!
March 22, 2023

Wake Up to the Importance of Sleep: Celebrating World Sleep Day!
March 18, 2023

Operations Management and AI: How Do They Work?
March 15, 2023
How Does BYOP(Bring Your Own Project) Help In Building Your Portfolio?

What Are the Ethics in Artificial Intelligence (AI)?
November 25, 2022

What is Epoch in Machine Learning?| UNext
November 24, 2022

The Impact Of Artificial Intelligence (AI) in Cloud Computing
November 18, 2022

Role of Artificial Intelligence and Machine Learning in Supply Chain Management
November 11, 2022

Best Python Libraries for Machine Learning in 2022
November 7, 2022
Are you ready to build your own career?
Query? Ask Us
Enter Your Details ×

- Machine Learning Basics
- Machine Learning - Home
- Machine Learning - Getting Started
- Machine Learning - Basic Concepts
- Machine Learning - Python Libraries
- Machine Learning - Applications
- Machine Learning - Life Cycle
- Machine Learning - Required Skills
- Machine Learning - Implementation
- Machine Learning - Challenges & Common Issues
- Machine Learning - Limitations
- Machine Learning - Reallife Examples
- Machine Learning - Data Structure
- Machine Learning - Mathematics
- Machine Learning - Artificial Intelligence
- Machine Learning - Neural Networks
- Machine Learning - Deep Learning
- Machine Learning - Getting Datasets
- Machine Learning - Categorical Data
- Machine Learning - Data Loading
- Machine Learning - Data Understanding
- Machine Learning - Data Preparation
- Machine Learning - Models
- Machine Learning - Supervised
- Machine Learning - Unsupervised
- Machine Learning - Semi-supervised
- Machine Learning - Reinforcement
- Machine Learning - Supervised vs. Unsupervised
- What Today’s AI Can Do?
- What is Machine Learning?
- Machine Learning - Categories
- Machine Learning - Scikit-learn Algorithm
- Machine Learning - Conclusion
- Machine Learning Data Visualization
- Machine Learning - Data Visualization
- Machine Learning - Histograms
- Machine Learning - Density Plots
- Machine Learning - Box and Whisker Plots
- Machine Learning - Correlation Matrix Plots
- Machine Learning - Scatter Matrix Plots
- Statistics for Machine Learning
- Machine Learning - Statistics
- Machine Learning - Mean, Median, Mode
- Machine Learning - Standard Deviation
- Machine Learning - Percentiles
- Machine Learning - Data Distribution
- Machine Learning - Skewness and Kurtosis
- Machine Learning - Bias and Variance
Machine Learning - Hypothesis
- Regression Analysis In ML
- Machine Learning - Regression Analysis
- Machine Learning - Linear Regression
- Machine Learning - Simple Linear Regression
- Machine Learning - Multiple Linear Regression
- Machine Learning - Polynomial Regression
- Classification Algorithms In ML
- Machine Learning - Classification Algorithms
- Machine Learning - Logistic Regression
- Machine Learning - K-Nearest Neighbors (KNN)
- Machine Learning - Naïve Bayes Algorithm
- Machine Learning - Decision Tree Algorithm
- Machine Learning - Support Vector Machine
- Machine Learning - Random Forest
- Machine Learning - Confusion Matrix
- Machine Learning - Stochastic Gradient Descent
- Clustering Algorithms In ML
- Machine Learning - Clustering Algorithms
- Machine Learning - Centroid-Based Clustering
- Machine Learning - K-Means Clustering
- Machine Learning - K-Medoids Clustering
- Machine Learning - Mean-Shift Clustering
- Machine Learning - Hierarchical Clustering
- Machine Learning - Density-Based Clustering
- Machine Learning - DBSCAN Clustering
- Machine Learning - OPTICS Clustering
- Machine Learning - HDBSCAN Clustering
- Machine Learning - BIRCH Clustering
- Machine Learning - Affinity Propagation
- Machine Learning - Distribution-Based Clustering
- Machine Learning - Agglomerative Clustering
- Dimensionality Reduction In ML
- Machine Learning - Dimensionality Reduction
- Machine Learning - Feature Selection
- Machine Learning - Feature Extraction
- Machine Learning - Backward Elimination
- Machine Learning - Forward Feature Construction
- Machine Learning - High Correlation Filter
- Machine Learning - Low Variance Filter
- Machine Learning - Missing Values Ratio
- Machine Learning - Principal Component Analysis
- Machine Learning Miscellaneous
- Machine Learning - Performance Metrics
- Machine Learning - Automatic Workflows
- Machine Learning - Boost Model Performance
- Machine Learning - Gradient Boosting
- Machine Learning - Bootstrap Aggregation (Bagging)
- Machine Learning - Cross Validation
- Machine Learning - AUC-ROC Curve
- Machine Learning - Grid Search
- Machine Learning - Data Scaling
- Machine Learning - Train and Test
- Machine Learning - Association Rules
- Machine Learning - Apriori Algorithm
- Machine Learning - Gaussian Discriminant Analysis
- Machine Learning - Cost Function
- Machine Learning - Bayes Theorem
- Machine Learning - Precision and Recall
- Machine Learning - Adversarial
- Machine Learning - Stacking
- Machine Learning - Epoch
- Machine Learning - Perceptron
- Machine Learning - Regularization
- Machine Learning - Overfitting
- Machine Learning - P-value
- Machine Learning - Entropy
- Machine Learning - MLOps
- Machine Learning - Data Leakage
- Machine Learning - Resources
- Machine Learning - Quick Guide
- Machine Learning - Useful Resources
- Machine Learning - Discussion
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
In machine learning, a hypothesis is a proposed explanation or solution for a problem. It is a tentative assumption or idea that can be tested and validated using data. In supervised learning, the hypothesis is the model that the algorithm is trained on to make predictions on unseen data.
The hypothesis is generally expressed as a function that maps input data to output labels. In other words, it defines the relationship between the input and output variables. The goal of machine learning is to find the best possible hypothesis that can generalize well to unseen data.
The process of finding the best hypothesis is called model training or learning. During the training process, the algorithm adjusts the model parameters to minimize the error or loss function, which measures the difference between the predicted output and the actual output.
Once the model is trained, it can be used to make predictions on new data. However, it is important to evaluate the performance of the model before using it in the real world. This is done by testing the model on a separate validation set or using cross-validation techniques.
Properties of a Good Hypothesis
The hypothesis plays a critical role in the success of a machine learning model. A good hypothesis should have the following properties −
Generalization − The model should be able to make accurate predictions on unseen data.
Simplicity − The model should be simple and interpretable, so that it is easier to understand and explain.
Robustness − The model should be able to handle noise and outliers in the data.
Scalability − The model should be able to handle large amounts of data efficiently.
There are many types of machine learning algorithms that can be used to generate hypotheses, including linear regression, logistic regression, decision trees, support vector machines, neural networks, and more.
What is Hypothesis in Machine Learning? How to Form a Hypothesis?

Hypothesis Testing is a broad subject that is applicable to many fields. When we study statistics, the Hypothesis Testing there involves data from multiple populations and the test is to see how significant the effect is on the population.
Top Machine Learning and AI Courses Online
| To Explore all our certification courses on AI & ML, kindly visit our page below. | ||
This involves calculating the p-value and comparing it with the critical value or the alpha. When it comes to Machine Learning, Hypothesis Testing deals with finding the function that best approximates independent features to the target. In other words, map the inputs to the outputs.
By the end of this tutorial, you will know the following:

- What is Hypothesis in Statistics vs Machine Learning
- What is Hypothesis space?
Process of Forming a Hypothesis
Trending machine learning skills.
Hypothesis in Statistics
A Hypothesis is an assumption of a result that is falsifiable, meaning it can be proven wrong by some evidence. A Hypothesis can be either rejected or failed to be rejected. We never accept any hypothesis in statistics because it is all about probabilities and we are never 100% certain. Before the start of the experiment, we define two hypotheses:
1. Null Hypothesis: says that there is no significant effect
2. Alternative Hypothesis: says that there is some significant effect
In statistics, we compare the P-value (which is calculated using different types of statistical tests) with the critical value or alpha. The larger the P-value, the higher is the likelihood, which in turn signifies that the effect is not significant and we conclude that we fail to reject the null hypothesis .
In other words, the effect is highly likely to have occurred by chance and there is no statistical significance of it. On the other hand, if we get a P-value very small, it means that the likelihood is small. That means the probability of the event occurring by chance is very low.
Join the ML and AI Course online from the World’s top Universities – Masters, Executive Post Graduate Programs, and Advanced Certificate Program in ML & AI to fast-track your career.
Significance Level
The Significance Level is set before starting the experiment. This defines how much is the tolerance of error and at which level can the effect can be considered significant. A common value for significance level is 95% which also means that there is a 5% chance of us getting fooled by the test and making an error. In other words, the critical value is 0.05 which acts as a threshold. Similarly, if the significance level was set at 99%, it would mean a critical value of 0.01%.
A statistical test is carried out on the population and sample to find out the P-value which then is compared with the critical value. If the P-value comes out to be less than the critical value, then we can conclude that the effect is significant and hence reject the Null Hypothesis (that said there is no significant effect). If P-Value comes out to be more than the critical value, we can conclude that there is no significant effect and hence fail to reject the Null Hypothesis.
Now, as we can never be 100% sure, there is always a chance of our tests being correct but the results being misleading. This means that either we reject the null when it is actually not wrong. It can also mean that we don’t reject the null when it is actually false. These are type 1 and type 2 errors of Hypothesis Testing.

Example
Consider you’re working for a vaccine manufacturer and your team develops the vaccine for Covid-19. To prove the efficacy of this vaccine, it needs to statistically proven that it is effective on humans. Therefore, we take two groups of people of equal size and properties. We give the vaccine to group A and we give a placebo to group B. We carry out analysis to see how many people in group A got infected and how many in group B got infected.
We test this multiple times to see if group A developed any significant immunity against Covid-19 or not. We calculate the P-value for all these tests and conclude that P-values are always less than the critical value. Hence, we can safely reject the null hypothesis and conclude there is indeed a significant effect.
Read: Machine Learning Models Explained
Hypothesis in Machine Learning
Hypothesis in Machine Learning is used when in a Supervised Machine Learning, we need to find the function that best maps input to output. This can also be called function approximation because we are approximating a target function that best maps feature to the target.
1. Hypothesis(h): A Hypothesis can be a single model that maps features to the target, however, may be the result/metrics. A hypothesis is signified by “ h ”.
2. Hypothesis Space(H): A Hypothesis space is a complete range of models and their possible parameters that can be used to model the data. It is signified by “ H ”. In other words, the Hypothesis is a subset of Hypothesis Space.
In essence, we have the training data (independent features and the target) and a target function that maps features to the target. These are then run on different types of algorithms using different types of configuration of their hyperparameter space to check which configuration produces the best results. The training data is used to formulate and find the best hypothesis from the hypothesis space. The test data is used to validate or verify the results produced by the hypothesis.
Consider an example where we have a dataset of 10000 instances with 10 features and one target. The target is binary, which means it is a binary classification problem. Now, say, we model this data using Logistic Regression and get an accuracy of 78%. We can draw the regression line which separates both the classes. This is a Hypothesis(h). Then we test this hypothesis on test data and get a score of 74%.
Checkout: Machine Learning Projects & Topics
Now, again assume we fit a RandomForests model on the same data and get an accuracy score of 85%. This is a good improvement over Logistic Regression already. Now we decide to tune the hyperparameters of RandomForests to get a better score on the same data. We do a grid search and run multiple RandomForest models on the data and check their performance. In this step, we are essentially searching the Hypothesis Space(H) to find a better function. After completing the grid search, we get the best score of 89% and we end the search.
FYI: Free nlp course !
Now we also try more models like XGBoost, Support Vector Machine and Naive Bayes theorem to test their performances on the same data. We then pick the best performing model and test it on the test data to validate its performance and get a score of 87%.
Popular AI and ML Blogs & Free Courses
| AI & ML Free Courses | ||
Before you go
The hypothesis is a crucial aspect of Machine Learning and Data Science. It is present in all the domains of analytics and is the deciding factor of whether a change should be introduced or not. Be it pharma, software, sales, etc. A Hypothesis covers the complete training dataset to check the performance of the models from the Hypothesis space.
A Hypothesis must be falsifiable, which means that it must be possible to test and prove it wrong if the results go against it. The process of searching for the best configuration of the model is time-consuming when a lot of different configurations need to be verified. There are ways to speed up this process as well by using techniques like Random Search of hyperparameters.
If you’re interested to learn more about machine learning, check out IIIT-B & upGrad’s Executive PG Programme in Machine Learning & AI which is designed for working professionals and offers 450+ hours of rigorous training, 30+ case studies & assignments, IIIT-B Alumni status, 5+ practical hands-on capstone projects & job assistance with top firms.

Pavan Vadapalli
Something went wrong
Our Trending Machine Learning Courses
- Advanced Certificate Programme in Machine Learning and NLP from IIIT Bangalore - Duration 8 Months
- Master of Science in Machine Learning & AI from LJMU - Duration 18 Months
- Executive PG Program in Machine Learning and AI from IIIT-B - Duration 12 Months
Machine Learning Skills To Master
- Artificial Intelligence Courses
- Tableau Courses
- NLP Courses
- Deep Learning Courses
Our Popular Machine Learning Course

Frequently Asked Questions (FAQs)
There are many reasons to do open-source projects. You are learning new things, you are helping others, you are networking with others, you are creating a reputation and many more. Open source is fun, and eventually you will get something back. One of the most important reasons is that it builds a portfolio of great work that you can present to companies and get hired. Open-source projects are a wonderful way to learn new things. You could be enhancing your knowledge of software development or you could be learning a new skill. There is no better way to learn than to teach.
Yes. Open-source projects do not discriminate. The open-source communities are made of people who love to write code. There is always a place for a newbie. You will learn a lot and also have the chance to participate in a variety of open-source projects. You will learn what works and what doesn't and you will also have the chance to make your code used by a large community of developers. There is a list of open-source projects that are always looking for new contributors.
GitHub offers developers a way to manage projects and collaborate with each other. It also serves as a sort of resume for developers, with a project's contributors, documentation, and releases listed. Contributions to a project show potential employers that you have the skills and motivation to work in a team. Projects are often more than code, so GitHub has a way that you can structure your project just like you would structure a website. You can manage your website with a branch. A branch is like an experiment or a copy of your website. When you want to experiment with a new feature or fix something, you make a branch and experiment there. If the experiment is successful, you can merge the branch back into the original website.
Explore Free Courses
Learn more about the education system, top universities, entrance tests, course information, and employment opportunities in Canada through this course.
Advance your career in the field of marketing with Industry relevant free courses
Build your foundation in one of the hottest industry of the 21st century
Master industry-relevant skills that are required to become a leader and drive organizational success
Build essential technical skills to move forward in your career in these evolving times
Get insights from industry leaders and career counselors and learn how to stay ahead in your career
Kickstart your career in law by building a solid foundation with these relevant free courses.
Stay ahead of the curve and upskill yourself on Generative AI and ChatGPT
Build your confidence by learning essential soft skills to help you become an Industry ready professional.
Learn more about the education system, top universities, entrance tests, course information, and employment opportunities in USA through this course.
Suggested Blogs
![hypothesis function in machine learning 15 Interesting MATLAB Project Ideas & Topics For Beginners [2024]](https://www.upgrad.com/__khugblog-next/image/?url=https%3A%2F%2Fd14b9ctw0m6fid.cloudfront.net%2Fugblog%2Fwp-content%2Fuploads%2F2020%2F05%2F561-metalab-projects.png&w=3840&q=75)
by Pavan Vadapalli
09 Jul 2024

07 Jul 2024

04 Jul 2024

03 Jul 2024

01 Jul 2024

26 Jun 2024

by MK Gurucharan
24 Jun 2024

21 Jun 2024
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
What exactly is a hypothesis space in machine learning?
Whilst I understand the term conceptually, I'm struggling to understand it operationally. Could anyone help me out by providing an example?
- machine-learning
- terminology
- $\begingroup$ A space where we can predict output by a set of some legal hypothesis (or function) and function is represented in terms of features. $\endgroup$ – Abhishek Kumar Commented Aug 9, 2019 at 17:03
3 Answers 3
Lets say you have an unknown target function $f:X \rightarrow Y$ that you are trying to capture by learning . In order to capture the target function you have to come up with some hypotheses, or you may call it candidate models denoted by H $h_1,...,h_n$ where $h \in H$ . Here, $H$ as the set of all candidate models is called hypothesis class or hypothesis space or hypothesis set .
For more information browse Abu-Mostafa's presentaton slides: https://work.caltech.edu/textbook.html
- 8 $\begingroup$ This answer conveys absolutely no information! What is the intended relationship between $f$, $h$, and $H$? What is meant by "hypothesis set"? $\endgroup$ – whuber ♦ Commented Nov 28, 2015 at 20:50
- 5 $\begingroup$ Please take a few minutes with our help center to learn about this site and its standards, JimBoy. $\endgroup$ – whuber ♦ Commented Nov 28, 2015 at 20:57
- $\begingroup$ The answer says very clear, h learns to capture target function f . H is the space where h1, h2,..hn got defined. $\endgroup$ – Logan Commented Nov 29, 2018 at 21:47
- $\begingroup$ @whuber I hope this is clearer $\endgroup$ – pentanol Commented Aug 6, 2021 at 8:51
- $\begingroup$ @pentanol You have succeeded in providing a different name for "hypothesis space," but without a definition or description of "candidate model," it doesn't seem to add any information to the post. What would be useful is information relevant to the questions that were posed, which concern "understand[ing] operationally" and a request for an example. $\endgroup$ – whuber ♦ Commented Aug 6, 2021 at 13:55
Suppose an example with four binary features and one binary output variable. Below is a set of observations:
This set of observations can be used by a machine learning (ML) algorithm to learn a function f that is able to predict a value y for any input from the input space .
We are searching for the ground truth f(x) = y that explains the relation between x and y for all possible inputs in the correct way.
The function f has to be chosen from the hypothesis space .
To get a better idea: The input space is in the above given example $2^4$ , its the number of possible inputs. The hypothesis space is $2^{2^4}=65536$ because for each set of features of the input space two outcomes ( 0 and 1 ) are possible.
The ML algorithm helps us to find one function , sometimes also referred as hypothesis, from the relatively large hypothesis space.
- A Few Useful Things to Know About ML
- 1 $\begingroup$ Just a small note on your answer: the size of the hypothesis space is indeed 65,536, but the a more easily explained expression for it would be $2^{(2^4)}$, since, there are $2^4$ possible unique samples, and thus $2^{(2^4)}$ possible label assignments for the entire input space. $\endgroup$ – engelen Commented Jan 10, 2018 at 9:52
- 1 $\begingroup$ @engelen Thanks for your advice, I've edited the answer. $\endgroup$ – So S Commented Jan 10, 2018 at 21:00
- $\begingroup$ @SoS That one function is called classifier?? $\endgroup$ – user125163 Commented Aug 22, 2018 at 16:26
- 2 $\begingroup$ @Arjun Hedge: Not the one, but one function that you learned is the classifier. The classifier could be (and that's your aim) the one function. $\endgroup$ – So S Commented Aug 22, 2018 at 16:50
The hypothesis space is very relevant to the topic of the so-called Bias-Variance Tradeoff in maximum likelihood. That's if the number of parameters in the model(hypothesis function) is too small for the model to fit the data(indicating underfitting and that the hypothesis space is too limited), the bias is high; while if the model you choose contains too many parameters than needed to fit the data the variance is high(indicating overfitting and that the hypothesis space is too expressive).
As stated in So S ' answer, if the parameters are discrete we can easily and concretely calculate how many possibilities are in the hypothesis space(or how large it is), but normally under realy life circumstances the parameters are continuous. Therefore generally the hypothesis space is uncountable.
Here is an example I borrowed and modified from the related part in the classical machine learning textbook: Pattern Recognition And Machine Learning to fit this question:
We are selecting a hypothesis function for an unknown function hidding in the training data given by a third person named CoolGuy living in an extragalactic planet. Let's say CoolGuy knows what the function is, because the data cases are provided by him and he just generated the data using the function. Let's call it(we only have the limited data and CoolGuy has both the unlimited data and the function generating them) the ground truth function and denote it by $y(x, w)$ .

The green curve is the $y(x,w)$ , and the little blue circles are the cases we have(they are not actually the true data cases transmitted by CoolGuy because of the it would be contaminated by some transmission noise, for example by macula or other things).
We thought that that hidden function would be very simple then we make an attempt at a linear model(make a hypothesis with a very limited space): $g_1(x, w)=w_0 + w_1 x$ with only two parameters: $w_0$ and $w_1$ , and we train the model use our data and we obtain this:

We can see that no matter how many data we use to fit the hypothesis it just doesn't work because it is not expressive enough.
So we try a much more expressive hypothesis: $g_9=\sum_j^9 w_j x^j $ with ten adaptive paramaters $w_0, w_1\cdots , w_9$ , and we also train the model and then we get:

We can see that it is just too expressive and fits all data cases. We see that a much larger hypothesis space( since $g_2$ can be expressed by $g_9$ by setting $w_2, w_3, \cdots, w_9$ as all 0 ) is more powerful than a simple hypothesis. But the generalization is also bad. That is, if we recieve more data from CoolGuy and to do reference, the trained model most likely fails in those unseen cases.
Then how large the hypothesis space is large enough for the training dataset? We can find an aswer from the textbook aforementioned:
One rough heuristic that is sometimes advocated is that the number of data points should be no less than some multiple (say 5 or 10) of the number of adaptive parameters in the model.
And you'll see from the textbook that if we try to use 4 parameters, $g_3=w_0+w_1 x + w_2 x^2 + w_3 x^3$ , the trained function is expressive enough for the underlying function $y=\sin(2\pi x)$ . It's kind a black art to find the number 3(the appropriate hypothesis space) in this case.
Then we can roughly say that the hypothesis space is the measure of how expressive you model is to fit the training data. The hypothesis that is expressive enough for the training data is the good hypothesis with an expressive hypothesis space. To test whether the hypothesis is good or bad we do the cross validation to see if it performs well in the validation data-set. If it is neither underfitting(too limited) nor overfititing(too expressive) the space is enough(according to Occam Razor a simpler one is preferable, but I digress).
- $\begingroup$ This approach looks relevant, but your explanation does not agree with that on p. 5 of your first reference: "A function $h:X\to\{0,1\}$ is called [an] hypothesis. A set $H$ of hypotheses among which the approximation function $y$ is searched is called [the] hypothesis space." (I would agree the slide is confusing, because its explanation implicitly requires that $C=\{0,1\}$, whereas that is generically labeled "classes" in the diagram. But let's not pass along that confusion: let's rectify it.) $\endgroup$ – whuber ♦ Commented Sep 24, 2016 at 15:33
- 1 $\begingroup$ @whuber I updated my answer just now more than two years later after I have learned more knowledge on the topic. Please help check if I can rectify it in a better way. Thanks. $\endgroup$ – Lerner Zhang Commented Feb 5, 2019 at 11:41
Not the answer you're looking for? Browse other questions tagged machine-learning terminology definition or ask your own question .
- Featured on Meta
- Upcoming initiatives on Stack Overflow and across the Stack Exchange network...
- Announcing a change to the data-dump process
Hot Network Questions
- "So, why would we possibly want to go there?" VS "So, why on earth would we want to go there?"
- Book series where soldiers or pilots from Earth are teleported to a world where they learn how to use crystal magic technology
- Flights canceled by travel agency (kiwi) without my approval
- What goods yield the best profit for time-travel arbitrage?
- How can I handle an ambitious colleague, promoted ahead of me, that is self-serving and not that great at his job?
- Is "Ἐλλάχ" the proper Greek transliteration of "Allah"?
- retain 0s before digit with siunitx /num notation
- How should I run cable across a steel beam?
- Sci-fi book about a boy who finds a portal to another dimension in his neighbor's playground set
- Why does "They be naked" use the base form of "be"?
- Narcissist boss won't allow me to move on
- Homebrew DND 5e Spell, review in power, and well... utility
- What does HJD-2450000 mean?
- Does the question "will I get transplanted" make sense to your ears?
- What was the purpose of the SCAN commands on the Intel 8272 / NEC μPD765 floppy disk controllers?
- Is "secco" really used in piano music?
- How to respect leading zero when importing in libreoffice calc
- Does color temperature limit how much a laser of a given wavelength can heat a target?
- Why are some elves royalty?
- Finding the processes trying to open some FIFO
- Constructing the interval [0, 1) via inverse powers of 2
- Why not use computers to evaluate strength of players?
- Is n-euclidean space a quotient of m-euclidean space?
- Maximizing row and column products in a 4x4 grid
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Newbie: What is the difference between hypothesis class and models?
I am new to machine learning and I am confused with the terminology. Thus far, I used to view a hypothesis class as different instance of hypothesis function... Example: If we are talking about linear classification then different lines characterized by different weights would together form the hypothesis class.
Is my understanding correct or can a hypothesis class represent anything which could approximate the target function? For instance, can a linear or quadratic function that approximates the target function together form a single hypothesis class or both are from different hypothesis classes?
- machine-learning
Your hypothesis class consists of all possible hypotheses that you are searching over, regardless of their form. For convenience's sake, the hypothesis class is usually constrained to be only one type of function or model at a time, since learning methods typically only work on one type at a time. This doesn't have to be the case, though:
- Hypothesis classes don't have to consist of only one type of function. If you're searching over all linear, quadratic, and exponential functions, then those are what your combined hypothesis class contains.
- Hypothesis classes also don't have to consist of only simple functions. If you manage to search over all piecewise-$\tanh^2$ functions, then those functions are what your hypothesis class includes.
The big tradeoff is that the larger your hypothesis class, the better the best hypothesis models the underlying true function, but the harder it is to find that best hypothesis. This is related to the bias–variance tradeoff .
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged machine-learning or ask your own question .
- The Overflow Blog
- The framework helping devs build LLM apps
- How to bridge the gap between Web2 skills and Web3 workflows
- Featured on Meta
- Upcoming initiatives on Stack Overflow and across the Stack Exchange network...
- Announcing a change to the data-dump process
Hot Network Questions
- Why are there two cables connected to this GFCI outlet?
- Finding the processes trying to open some FIFO
- Are missiles aircraft?
- A Diophantine equation involving divisor counting function?
- Can you find a real example of "time travel" caused by undefined behaviour?
- What was the purpose of the SCAN commands on the Intel 8272 / NEC μPD765 floppy disk controllers?
- How should I run cable across a steel beam?
- Are operators unitary on a real quantum computer?
- Why can THHN/THWN go in Schedule 40 PVC but NM cable (Romex) requires Schedule 80?
- Objects proven finiteness yet no algorithm discovered?
- What sort of security does Docusign provide?
- What are the ways compilers recognize complex patterns?
- Homebrew DND 5e Spell, review in power, and well... utility
- What is the meaning of the "Super 8 - Interactive Teaser" under "EXTRAS" in Portal 2?
- Complexity of permutation group intersection
- Always orient a sundial towards polar north?
- Why is this image from pianochord.org for A11 labeled as an inversion, when its lowest pitch note is an A?
- Teaching students how to check the validity of their proofs
- Why does "They be naked" use the base form of "be"?
- Are Windows ReFS file-level snapshots what File History should have been?
- Maximizing row and column products in a 4x4 grid
- Reorder for smallest largest prefix sum
- Knights, Knaves, and Spies
- Why is restructure of mempool required with cluster mempool?
- Stack Overflow for Teams Where developers & technologists share private knowledge with coworkers
- Advertising & Talent Reach devs & technologists worldwide about your product, service or employer brand
- OverflowAI GenAI features for Teams
- OverflowAPI Train & fine-tune LLMs
- Labs The future of collective knowledge sharing
- About the company Visit the blog
Collectives™ on Stack Overflow
Find centralized, trusted content and collaborate around the technologies you use most.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Get early access and see previews of new features.
How to choose the degree of a Hypothesis function? [closed]
In a normal machine learning problem you get many features(eg:- if you are making an image recogniser), so when there are many features you can't visualise the data(you can't plot a graph). Without plotting a graph is there a way to determine what degree of a hypothesis function should we use for that problem? How to determine the best hypothesis functions to use? eg:-
if there are 2 inputs x(1),x(2).
whether to choose (w0) + x(1)*w(1) + x(2)*w(2) as the hypothesis function or
w(0) + x(1)*w(1) + x(2)*w(2) + x(1)*x(2)*w(3) + (x(1)^2)*w(4) + (x(2)^2)*w(5)
as the hypothesis function :where w(0),w(1),w(2),w(3)...... are weights.
- machine-learning
- scientific-computing
- non-linear-regression
- 1 Normally, you'd either evaluate various feature sets (or kernels) on a test set and measure something like accuracy or F1-score. But this question is really off-topic; try metaoptimize.com/qa or stats.stackexchange.com – Fred Foo Commented Oct 11, 2012 at 9:50
- @larsmans That is how you train your hypothesis function right? I want to know how to choose the degree of the hypothesis function. If one choose a 2nd degree hypothesis function, using your training set you can get the optimum 2nd degree hypothesis function(by training). If one choose a 3rd degree hypothesis function, by training you can get the optimum 3rd degree hypothesis function. But the optimum 2nd degree hypothesis function might be better/worse than the optimum 3rd degree hypothesis function. I want to know how to choose the most optimum "degree" for the hypothesis function. – sachira Commented Oct 11, 2012 at 10:09
- No, you train on a training set. Then you test on a held-out test set to see how well your optimal solution for the training set generalizes to unseen data. – Fred Foo Commented Oct 11, 2012 at 10:36
- 1 @larsmans Yes. But training is done to optimize a given/chosen hypothesis right? But how to find whether a 2nd degree hypothesis would be better or 3rd degree hypothesis would be better or........nth degree hypothesis would be better? (n=1,2,3,4,......) – sachira Commented Oct 11, 2012 at 14:11
- By what I said in my first answer, evaluating it on a test set. I can keep repeating what I said, but maybe you'd better read a book on machine learning, e.g. ESL . – Fred Foo Commented Oct 11, 2012 at 14:22
The first major step to apply is feature selection or feature extraction ( dimensionality reduction ). This is a pre-processing step that you can apply using certain relevance metrics like correlation, mutual-information as mRmR. Also, there are other methods stimulated by the domain of numerical linear algebra and statistics such as principle component analysis for finding features describing the space based on some assumptions.
Your question is related to a major concern in the field of machine learning known as model selection. The only way to know which degree to use is to experiment with models of different degrees (d=1, d=2, ...) keeping in mind the following:
1- Overfitting: you need to avoid overfitting by making sure that you limit the ranges of the variables (the Ws in your case). This solution is known as regularization . Also, try not to train the classifier for long time like in the case of ANN.
2- Prapring training, validation and testing sets. Training is for training the model, validation is for tuning the parameters and testing is for comparing different models.
3- Proper choice of the performance evaluation metric . If your training data is not well-balanced (i.e. nearly the same number of samples is assigned for each value or class lable of your target variable), then accuracy is not indicative. In this case, you may need to consider sensitivity, specificity or Mathew correlation.
Experiments is the key and indeed you are limited by resources. Nevertheless, proper design of the experiment could serve your purpose.
Not the answer you're looking for? Browse other questions tagged machine-learning regression scientific-computing non-linear-regression or ask your own question .
- The Overflow Blog
- The framework helping devs build LLM apps
- How to bridge the gap between Web2 skills and Web3 workflows
- Featured on Meta
- Upcoming initiatives on Stack Overflow and across the Stack Exchange network...
- Announcing a change to the data-dump process
- What makes a homepage useful for logged-in users
Hot Network Questions
- Wait, ASCII was 128 characters all along?
- Would it be possible to start a new town in America with its own political system?
- Why does "They be naked" use the base form of "be"?
- Did Arab Christians use the word "Allah" before Islam?
- What is the meaning of the "Super 8 - Interactive Teaser" under "EXTRAS" in Portal 2?
- Could today's flash memory be used instead of RAM in 1980s 8 bit machines?
- Can your boss take vouchers from you, offered from suppliers?
- Finding the processes trying to open some FIFO
- Mutual Life Insurance Company of New York -- What is it now? How can I reach them?
- Left crank arm misaligned on climb
- Is deciding to use google fonts the sort of decision that makes an entity a controller rather than a processor?
- What's to prevent us from concluding that Revelation 13:3 has been fulfilled through Trump?
- How much coolant drip is normal on old car without overflow tank
- Is n-euclidean space a quotient of m-euclidean space?
- What does HJD-2450000 mean?
- Are Windows ReFS file-level snapshots what File History should have been?
- How to pronounce Türkiye in English?
- Teaching students how to check the validity of their proofs
- Why are some elves royalty?
- Physical meaning of symmetric and antisymmetric wavefunction
- When can widening conversions cause problems?
- Is the XOR of hashes a good hash function?
- Why is restructure of mempool required with cluster mempool?
- Why can THHN/THWN go in Schedule 40 PVC but NM cable (Romex) requires Schedule 80?
- School Guide
- Mathematics
- Number System and Arithmetic
- Trigonometry
- Probability
- Mensuration
- Maths Formulas
- Class 8 Maths Notes
- Class 9 Maths Notes
- Class 10 Maths Notes
- Class 11 Maths Notes
- Class 12 Maths Notes
Hypothesis is a testable statement that explains what is happening or observed. It proposes the relation between the various participating variables. Hypothesis is also called Theory, Thesis, Guess, Assumption, or Suggestion. Hypothesis creates a structure that guides the search for knowledge.
In this article, we will learn what is hypothesis, its characteristics, types, and examples. We will also learn how hypothesis helps in scientific research.

Table of Content
What is Hypothesis?
Hypothesis meaning, characteristics of hypothesis, sources of hypothesis, types of hypothesis, simple hypothesis, complex hypothesis, directional hypothesis, non-directional hypothesis, null hypothesis (h0), alternative hypothesis (h1 or ha), statistical hypothesis, research hypothesis, associative hypothesis, causal hypothesis, hypothesis examples, simple hypothesis example, complex hypothesis example, directional hypothesis example, non-directional hypothesis example, alternative hypothesis (ha), functions of hypothesis, how hypothesis help in scientific research.
A hypothesis is a suggested idea or plan that has little proof, meant to lead to more study. It’s mainly a smart guess or suggested answer to a problem that can be checked through study and trial. In science work, we make guesses called hypotheses to try and figure out what will happen in tests or watching. These are not sure things but rather ideas that can be proved or disproved based on real-life proofs. A good theory is clear and can be tested and found wrong if the proof doesn’t support it.
A hypothesis is a proposed statement that is testable and is given for something that happens or observed.
- It is made using what we already know and have seen, and it’s the basis for scientific research.
- A clear guess tells us what we think will happen in an experiment or study.
- It’s a testable clue that can be proven true or wrong with real-life facts and checking it out carefully.
- It usually looks like a “if-then” rule, showing the expected cause and effect relationship between what’s being studied.
Here are some key characteristics of a hypothesis:
- Testable: An idea (hypothesis) should be made so it can be tested and proven true through doing experiments or watching. It should show a clear connection between things.
- Specific: It needs to be easy and on target, talking about a certain part or connection between things in a study.
- Falsifiable: A good guess should be able to show it’s wrong. This means there must be a chance for proof or seeing something that goes against the guess.
- Logical and Rational: It should be based on things we know now or have seen, giving a reasonable reason that fits with what we already know.
- Predictive: A guess often tells what to expect from an experiment or observation. It gives a guide for what someone might see if the guess is right.
- Concise: It should be short and clear, showing the suggested link or explanation simply without extra confusion.
- Grounded in Research: A guess is usually made from before studies, ideas or watching things. It comes from a deep understanding of what is already known in that area.
- Flexible: A guess helps in the research but it needs to change or fix when new information comes up.
- Relevant: It should be related to the question or problem being studied, helping to direct what the research is about.
- Empirical: Hypotheses come from observations and can be tested using methods based on real-world experiences.
Hypotheses can come from different places based on what you’re studying and the kind of research. Here are some common sources from which hypotheses may originate:
- Existing Theories: Often, guesses come from well-known science ideas. These ideas may show connections between things or occurrences that scientists can look into more.
- Observation and Experience: Watching something happen or having personal experiences can lead to guesses. We notice odd things or repeat events in everyday life and experiments. This can make us think of guesses called hypotheses.
- Previous Research: Using old studies or discoveries can help come up with new ideas. Scientists might try to expand or question current findings, making guesses that further study old results.
- Literature Review: Looking at books and research in a subject can help make guesses. Noticing missing parts or mismatches in previous studies might make researchers think up guesses to deal with these spots.
- Problem Statement or Research Question: Often, ideas come from questions or problems in the study. Making clear what needs to be looked into can help create ideas that tackle certain parts of the issue.
- Analogies or Comparisons: Making comparisons between similar things or finding connections from related areas can lead to theories. Understanding from other fields could create new guesses in a different situation.
- Hunches and Speculation: Sometimes, scientists might get a gut feeling or make guesses that help create ideas to test. Though these may not have proof at first, they can be a beginning for looking deeper.
- Technology and Innovations: New technology or tools might make guesses by letting us look at things that were hard to study before.
- Personal Interest and Curiosity: People’s curiosity and personal interests in a topic can help create guesses. Scientists could make guesses based on their own likes or love for a subject.
Here are some common types of hypotheses:
- Non-directional Hypothesis
Simple Hypothesis guesses a connection between two things. It says that there is a connection or difference between variables, but it doesn’t tell us which way the relationship goes.
Complex Hypothesis tells us what will happen when more than two things are connected. It looks at how different things interact and may be linked together.
Directional Hypothesis says how one thing is related to another. For example, it guesses that one thing will help or hurt another thing.
Non-Directional Hypothesis are the one that don’t say how the relationship between things will be. They just say that there is a connection, without telling which way it goes.
Null hypothesis is a statement that says there’s no connection or difference between different things. It implies that any seen impacts are because of luck or random changes in the information.
Alternative Hypothesis is different from the null hypothesis and shows that there’s a big connection or gap between variables. Scientists want to say no to the null hypothesis and choose the alternative one.
Statistical Hypotheis are used in math testing and include making ideas about what groups or bits of them look like. You aim to get information or test certain things using these top-level, common words only.
Research Hypothesis comes from the research question and tells what link is expected between things or factors. It leads the study and chooses where to look more closely.
Associative Hypotheis guesses that there is a link or connection between things without really saying it caused them. It means that when one thing changes, it is connected to another thing changing.
Causal Hypothesis are different from other ideas because they say that one thing causes another. This means there’s a cause and effect relationship between variables involved in the situation. They say that when one thing changes, it directly makes another thing change.
Following are the examples of hypotheses based on their types:
- Studying more can help you do better on tests.
- Getting more sun makes people have higher amounts of vitamin D.
- How rich you are, how easy it is to get education and healthcare greatly affects the number of years people live.
- A new medicine’s success relies on the amount used, how old a person is who takes it and their genes.
- Drinking more sweet drinks is linked to a higher body weight score.
- Too much stress makes people less productive at work.
- Drinking caffeine can affect how well you sleep.
- People often like different kinds of music based on their gender.
- The average test scores of Group A and Group B are not much different.
- There is no connection between using a certain fertilizer and how much it helps crops grow.
- Patients on Diet A have much different cholesterol levels than those following Diet B.
- Exposure to a certain type of light can change how plants grow compared to normal sunlight.
- The average smarts score of kids in a certain school area is 100.
- The usual time it takes to finish a job using Method A is the same as with Method B.
- Having more kids go to early learning classes helps them do better in school when they get older.
- Using specific ways of talking affects how much customers get involved in marketing activities.
- Regular exercise helps to lower the chances of heart disease.
- Going to school more can help people make more money.
- Playing violent video games makes teens more likely to act aggressively.
- Less clean air directly impacts breathing health in city populations.
Hypotheses have many important jobs in the process of scientific research. Here are the key functions of hypotheses:
- Guiding Research: Hypotheses give a clear and exact way for research. They act like guides, showing the predicted connections or results that scientists want to study.
- Formulating Research Questions: Research questions often create guesses. They assist in changing big questions into particular, checkable things. They guide what the study should be focused on.
- Setting Clear Objectives: Hypotheses set the goals of a study by saying what connections between variables should be found. They set the targets that scientists try to reach with their studies.
- Testing Predictions: Theories guess what will happen in experiments or observations. By doing tests in a planned way, scientists can check if what they see matches the guesses made by their ideas.
- Providing Structure: Theories give structure to the study process by arranging thoughts and ideas. They aid scientists in thinking about connections between things and plan experiments to match.
- Focusing Investigations: Hypotheses help scientists focus on certain parts of their study question by clearly saying what they expect links or results to be. This focus makes the study work better.
- Facilitating Communication: Theories help scientists talk to each other effectively. Clearly made guesses help scientists to tell others what they plan, how they will do it and the results expected. This explains things well with colleagues in a wide range of audiences.
- Generating Testable Statements: A good guess can be checked, which means it can be looked at carefully or tested by doing experiments. This feature makes sure that guesses add to the real information used in science knowledge.
- Promoting Objectivity: Guesses give a clear reason for study that helps guide the process while reducing personal bias. They motivate scientists to use facts and data as proofs or disprovals for their proposed answers.
- Driving Scientific Progress: Making, trying out and adjusting ideas is a cycle. Even if a guess is proven right or wrong, the information learned helps to grow knowledge in one specific area.
Researchers use hypotheses to put down their thoughts directing how the experiment would take place. Following are the steps that are involved in the scientific method:
- Initiating Investigations: Hypotheses are the beginning of science research. They come from watching, knowing what’s already known or asking questions. This makes scientists make certain explanations that need to be checked with tests.
- Formulating Research Questions: Ideas usually come from bigger questions in study. They help scientists make these questions more exact and testable, guiding the study’s main point.
- Setting Clear Objectives: Hypotheses set the goals of a study by stating what we think will happen between different things. They set the goals that scientists want to reach by doing their studies.
- Designing Experiments and Studies: Assumptions help plan experiments and watchful studies. They assist scientists in knowing what factors to measure, the techniques they will use and gather data for a proposed reason.
- Testing Predictions: Ideas guess what will happen in experiments or observations. By checking these guesses carefully, scientists can see if the seen results match up with what was predicted in each hypothesis.
- Analysis and Interpretation of Data: Hypotheses give us a way to study and make sense of information. Researchers look at what they found and see if it matches the guesses made in their theories. They decide if the proof backs up or disagrees with these suggested reasons why things are happening as expected.
- Encouraging Objectivity: Hypotheses help make things fair by making sure scientists use facts and information to either agree or disagree with their suggested reasons. They lessen personal preferences by needing proof from experience.
- Iterative Process: People either agree or disagree with guesses, but they still help the ongoing process of science. Findings from testing ideas make us ask new questions, improve those ideas and do more tests. It keeps going on in the work of science to keep learning things.
People Also View:
Mathematics Maths Formulas Branches of Mathematics
Summary – Hypothesis
A hypothesis is a testable statement serving as an initial explanation for phenomena, based on observations, theories, or existing knowledge. It acts as a guiding light for scientific research, proposing potential relationships between variables that can be empirically tested through experiments and observations.
The hypothesis must be specific, testable, falsifiable, and grounded in prior research or observation, laying out a predictive, if-then scenario that details a cause-and-effect relationship. It originates from various sources including existing theories, observations, previous research, and even personal curiosity, leading to different types, such as simple, complex, directional, non-directional, null, and alternative hypotheses, each serving distinct roles in research methodology .
The hypothesis not only guides the research process by shaping objectives and designing experiments but also facilitates objective analysis and interpretation of data , ultimately driving scientific progress through a cycle of testing, validation, and refinement.
Hypothesis – FAQs
What is a hypothesis.
A guess is a possible explanation or forecast that can be checked by doing research and experiments.
What are Components of a Hypothesis?
The components of a Hypothesis are Independent Variable, Dependent Variable, Relationship between Variables, Directionality etc.
What makes a Good Hypothesis?
Testability, Falsifiability, Clarity and Precision, Relevance are some parameters that makes a Good Hypothesis
Can a Hypothesis be Proven True?
You cannot prove conclusively that most hypotheses are true because it’s generally impossible to examine all possible cases for exceptions that would disprove them.
How are Hypotheses Tested?
Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data
Can Hypotheses change during Research?
Yes, you can change or improve your ideas based on new information discovered during the research process.
What is the Role of a Hypothesis in Scientific Research?
Hypotheses are used to support scientific research and bring about advancements in knowledge.

Please Login to comment...
Similar reads.
- Geeks Premier League
- School Learning
- Geeks Premier League 2023
- Maths-Class-12
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.
- View all journals
- Explore content
- About the journal
- Publish with us
- Sign up for alerts
- Open access
- Published: 09 July 2024
Automating psychological hypothesis generation with AI: when large language models meet causal graph
- Song Tong ORCID: orcid.org/0000-0002-4183-8454 1 , 2 , 3 , 4 na1 ,
- Kai Mao 5 na1 ,
- Zhen Huang 2 ,
- Yukun Zhao 2 &
- Kaiping Peng 1 , 2 , 3 , 4
Humanities and Social Sciences Communications volume 11 , Article number: 896 ( 2024 ) Cite this article
654 Accesses
4 Altmetric
Metrics details
- Science, technology and society
Leveraging the synergy between causal knowledge graphs and a large language model (LLM), our study introduces a groundbreaking approach for computational hypothesis generation in psychology. We analyzed 43,312 psychology articles using a LLM to extract causal relation pairs. This analysis produced a specialized causal graph for psychology. Applying link prediction algorithms, we generated 130 potential psychological hypotheses focusing on “well-being”, then compared them against research ideas conceived by doctoral scholars and those produced solely by the LLM. Interestingly, our combined approach of a LLM and causal graphs mirrored the expert-level insights in terms of novelty, clearly surpassing the LLM-only hypotheses ( t (59) = 3.34, p = 0.007 and t (59) = 4.32, p < 0.001, respectively). This alignment was further corroborated using deep semantic analysis. Our results show that combining LLM with machine learning techniques such as causal knowledge graphs can revolutionize automated discovery in psychology, extracting novel insights from the extensive literature. This work stands at the crossroads of psychology and artificial intelligence, championing a new enriched paradigm for data-driven hypothesis generation in psychological research.
Similar content being viewed by others
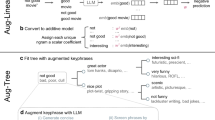
Augmenting interpretable models with large language models during training

ThoughtSource: A central hub for large language model reasoning data

Testing theory of mind in large language models and humans
Introduction.
In an age in which the confluence of artificial intelligence (AI) with various subjects profoundly shapes sectors ranging from academic research to commercial enterprises, dissecting the interplay of these disciplines becomes paramount (Williams et al., 2023 ). In particular, psychology, which serves as a nexus between the humanities and natural sciences, consistently endeavors to demystify the complex web of human behaviors and cognition (Hergenhahn and Henley, 2013 ). Its profound insights have significantly enriched academia, inspiring innovative applications in AI design. For example, AI models have been molded on hierarchical brain structures (Cichy et al., 2016 ) and human attention systems (Vaswani et al., 2017 ). Additionally, these AI models reciprocally offer a rejuvenated perspective, deepening our understanding from the foundational cognitive taxonomy to nuanced esthetic perceptions (Battleday et al., 2020 ; Tong et al., 2021 ). Nevertheless, the multifaceted domain of psychology, particularly social psychology, has exhibited a measured evolution compared to its tech-centric counterparts. This can be attributed to its enduring reliance on conventional theory-driven methodologies (Henrich et al., 2010 ; Shah et al., 2015 ), a characteristic that stands in stark contrast to the burgeoning paradigms of AI and data-centric research (Bechmann and Bowker, 2019 ; Wang et al., 2023 ).
In the journey of psychological research, each exploration originates from a spark of innovative thought. These research trajectories may arise from established theoretical frameworks, daily event insights, anomalies within data, or intersections of interdisciplinary discoveries (Jaccard and Jacoby, 2019 ). Hypothesis generation is pivotal in psychology (Koehler, 1994 ; McGuire, 1973 ), as it facilitates the exploration of multifaceted influencers of human attitudes, actions, and beliefs. The HyGene model (Thomas et al., 2008 ) elucidated the intricacies of hypothesis generation, encompassing the constraints of working memory and the interplay between ambient and semantic memories. Recently, causal graphs have provided psychology with a systematic framework that enables researchers to construct and simulate intricate systems for a holistic view of “bio-psycho-social” interactions (Borsboom et al., 2021 ; Crielaard et al., 2022 ). Yet, the labor-intensive nature of the methodology poses challenges, which requires multidisciplinary expertise in algorithmic development, exacerbating the complexities (Crielaard et al., 2022 ). Meanwhile, advancements in AI, exemplified by models such as the generative pretrained transformer (GPT), present new avenues for creativity and hypothesis generation (Wang et al., 2023 ).
Building on this, notably large language models (LLMs) such as GPT-3, GPT-4, and Claude-2, which demonstrate profound capabilities to comprehend and infer causality from natural language texts, a promising path has emerged to extract causal knowledge from vast textual data (Binz and Schulz, 2023 ; Gu et al., 2023 ). Exciting possibilities are seen in specific scenarios in which LLMs and causal graphs manifest complementary strengths (Pan et al., 2023 ). Their synergistic combination converges human analytical and systemic thinking, echoing the holistic versus analytic cognition delineated in social psychology (Nisbett et al., 2001 ). This amalgamation enables fine-grained semantic analysis and conceptual understanding via LLMs, while causal graphs offer a global perspective on causality, alleviating the interpretability challenges of AI (Pan et al., 2023 ). This integrated methodology efficiently counters the inherent limitations of working and semantic memories in hypothesis generation and, as previous academic endeavors indicate, has proven efficacious across disciplines. For example, a groundbreaking study in physics synthesized 750,000 physics publications, utilizing cutting-edge natural language processing to extract 6368 pivotal quantum physics concepts, culminating in a semantic network forecasting research trajectories (Krenn and Zeilinger, 2020 ). Additionally, by integrating knowledge-based causal graphs into the foundation of the LLM, the LLM’s capability for causative inference significantly improves (Kıcıman et al., 2023 ).
To this end, our study seeks to build a pioneering analytical framework, combining the semantic and conceptual extraction proficiency of LLMs with the systemic thinking of the causal graph, with the aim of crafting a comprehensive causal network of semantic concepts within psychology. We meticulously analyzed 43,312 psychological articles, devising an automated method to construct a causal graph, and systematically mining causative concepts and their interconnections. Specifically, the initial sifting and preparation of the data ensures a high-quality corpus, and is followed by employing advanced extraction techniques to identify standardized causal concepts. This results in a graph database that serves as a reservoir of causal knowledge. In conclusion, using node embedding and similarity-based link prediction, we unearthed potential causal relationships, and thus generated the corresponding hypotheses.
To gauge the pragmatic value of our network, we selected 130 hypotheses on “well-being” generated by our framework, comparing them with hypotheses crafted by novice experts (doctoral students in psychology) and the LLM models. The results are encouraging: Our algorithm matches the caliber of novice experts, outshining the hypotheses generated solely by the LLM models in novelty. Additionally, through deep semantic analysis, we demonstrated that our algorithm contains more profound conceptual incorporations and a broader semantic spectrum.
Our study advances the field of psychology in two significant ways. Firstly, it extracts invaluable causal knowledge from the literature and converts it to visual graphics. These aids can feed algorithms to help deduce more latent causal relations and guide models in generating a plethora of novel causal hypotheses. Secondly, our study furnishes novel tools and methodologies for causal analysis and scientific knowledge discovery, representing the seamless fusion of modern AI with traditional research methodologies. This integration serves as a bridge between conventional theory-driven methodologies in psychology and the emerging paradigms of data-centric research, thereby enriching our understanding of the factors influencing psychology, especially within the realm of social psychology.
Methodological framework for hypothesis generation
The proposed LLM-based causal graph (LLMCG) framework encompasses three steps: literature retrieval, causal pair extraction, and hypothesis generation, as illustrated in Fig. 1 . In the literature gathering phase, ~140k psychology-related articles were downloaded from public databases. In step two, GPT-4 were used to distil causal relationships from these articles, culminating in the creation of a causal relationship network based on 43,312 selected articles. In the third step, an in-depth examination of these data was executed, adopting link prediction algorithms to forecast the dynamics within the causal relationship network for searching the highly potential causality concept pairs.
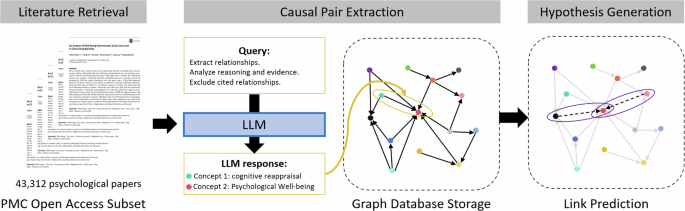
Note: LLM stands for large language model; LLMCG algorithm stands for LLM-based causal graph algorithm, which includes the processes of literature retrieval, causal pair extraction, and hypothesis generation.
Step 1: Literature retrieval
The primary data source for this study was a public repository of scientific articles, the PMC Open Access Subset. Our decision to utilize this repository was informed by several key attributes that it possesses. The PMC Open Access Subset boasts an expansive collection of over 2 million full-text XML science and medical articles, providing a substantial and diverse base from which to derive insights for our research. Furthermore, the open-access nature of the articles not only enhances the transparency and reproducibility of our methodology, but also ensures that the results and processes can be independently accessed and verified by other researchers. Notably, the content within this subset originates from recognized journals, all of which have undergone rigorous peer review, lending credence to the quality and reliability of the data we leveraged. Finally, an added advantage was the rich metadata accompanying each article. These metadata were instrumental in refining our article selection process, ensuring coherent thematic alignment with our research objectives in the domains of psychology.
To identify articles relevant to our study, we applied a series of filtering criteria. First, the presence of certain keywords within article titles or abstracts was mandatory. Some examples of these keywords include “psychol”, “clin psychol”, and “biol psychol”. Second, we exploited the metadata accompanying each article. The classification of articles based on these metadata ensured alignment with recognized thematic standards in the domains of psychology and neuroscience. Upon the application of these criteria, we managed to curate a subset of approximately 140K articles that most likely discuss causal concepts in both psychology and neuroscience.
Step 2: Causal pair extraction
The process of extracting causal knowledge from vast troves of scientific literature is intricate and multifaceted. Our methodology distils this complex process into four coherent steps, each serving a distinct purpose. (1) Article selection and cost analysis: Determines the feasibility of processing a specific volume of articles, ensuring optimal resource allocation. (2) Text extraction and analysis: Ensures the purity of the data that enter our causal extraction phase by filtering out nonrelevant content. (3) Causal knowledge extraction: Uses advanced language models to detect, classify, and standardize causal factors relationships present in texts. (4) Graph database storage: Facilitates structured storage, easy retrieval, and the possibility of advanced relational analyses for future research. This streamlined approach ensures accuracy, consistency, and scalability in our endeavor to understand the interplay of causal concepts in psychology and neuroscience.
Text extraction and cleaning
After a meticulous cost analysis detailed in Appendix A , our selection process identified 43,312 articles. This selection was strategically based on the criterion that the journal titles must incorporate the term “Psychol”, signifying their direct relevance to the field of psychology. The distributions of publication sources and years can be found in Table 1 . Extracting the full texts of the articles from their PDF sources was an essential initial step, and, for this purpose, the PyPDF2 Python library was used. This library allowed us to seamlessly extract and concatenate titles, abstracts, and main content from each PDF article. However, a challenge arose with the presence of extraneous sections such as references or tables, in the extracted texts. The implemented procedure, employing regular expressions in Python, was not only adept at identifying variations of the term “references” but also ascertained whether this section appeared as an isolated segment. This check was critical to ensure that the identified that the “references” section was indeed distinct, marking the start of a reference list without continuation into other text. Once identified as a standalone entity, the next step in the method was to efficiently remove the reference section and its subsequent content.
Causal knowledge extraction method
In our effort to extract causal knowledge, the choice of GPT-4 was not arbitrary. While several models were available for such tasks, GPT-4 emerged as a frontrunner due to its advanced capabilities (Wu et al., 2023 ), extensive training on diverse data, with its proven proficiency in understanding context, especially in complex scientific texts (Cheng et al., 2023 ; Sanderson, 2023 ). Other models were indeed considered; however, the capacity of GPT-4 to generate coherent, contextually relevant responses gave our project an edge in its specific requirements.
The extraction process commenced with the segmentation of the articles. Due to the token constraints inherent to GPT-4, it was imperative to break down the articles into manageable chunks, specifically those of 4000 tokens or fewer. This approach ensured a comprehensive interpretation of the content without omitting any potential causal relationships. The next phase was prompt engineering. To effectively guide the extraction capabilities of GPT-4, we crafted explicit prompts. A testament to this meticulous engineering is demonstrated in a directive in which we asked the model to elucidate causal pairs in a predetermined JSON format. For a clearer understanding, readers are referred to Table 2 , which elucidates the example prompt and the subsequent model response. After extraction, the outputs were not immediately cataloged. A filtering process was initiated to ascertain the standardization of the concept pairs. This process weeded out suboptimal outputs. Aiding in this quality control, GPT-4 played a pivotal role in the verification of causal pairs, determining their relevance, causality, and ensuring correct directionality. Finally, while extracting knowledge, we were aware of the constraints imposed by the GPT-4 API. There was a conscious effort to ensure that we operated within the bounds of 60 requests and 150k tokens per minute. This interplay of prompt engineering and stringent filtering was productive.
In addition, we conducted an exploratory study to assess GPT-4’s discernment between “causality” and “correlation” involved four graduate students (mean age 31 ± 10.23), each evaluating relationship pairs extracted from their familiar psychology articles. The experimental details and results can be found in Appendix A and Table A1. The results showed that out of 289 relationships identified by GPT-4, 87.54% were validated. Notably, when GPT-4 classified relationships as causal, only 13.02% (31/238) were recognized as non-relationship, while 65.55% (156/238) agreed upon as causality. This shows that GPT-4 can accurately extract relationships (causality or correlation) in psychological texts, underscoring the potential as a tool for the construction of causal graphs.
To enhance the robustness of the extracted causal relationships and minimize biases, we adopted a multifaceted approach. Recognizing the indispensable role of human judgment, we periodically subjected random samples of extracted causal relationships to the scrutiny of domain experts. Their valuable feedback was instrumental in the real-time fine-tuning the extraction process. Instead of heavily relying on referenced hypotheses, our focus was on extracting causal pairs, primarily from the findings mentioned in the main texts. This systematic methodology ultimately resulted in a refined text corpus distilled from 43,312 articles, which contained many conceptual insights and were primed for rigorous causal extraction.
Graph database storage
Our decision to employ Neo4j as the database system was strategic. Neo4j, as a graph database (Thomer and Wickett, 2020 ), is inherently designed to capture and represent complex relationships between data points, an attribute that is essential for understanding intricate causal relationships. Beyond its technical prowess, Neo4j provides advantages such as scalability, resilience, and efficient querying capabilities (Webber, 2012 ). It is particularly adept at traversing interconnected data points, making it an excellent fit for our causal relationship analysis. The mined causal knowledge finds its abode in the Neo4j graph database. Each pair of causal concepts is represented as a node, with its directionality and interpretations stored as attributes. Relationships provide related concepts together. Storing the knowledge graph in Neo4j allows for the execution of the graph algorithms to analyze concept interconnectivity and reveal potential relationships.
The graph database contains 197k concepts and 235k connections. Table 3 encapsulates the core concepts and provides a vivid snapshot of the most recurring themes; helping us to understand the central topics that dominate the current psychological discourse. A comprehensive examination of the core concepts extracted from 43,312 psychological papers, several distinct patterns and focal areas emerged. In particular, there is a clear balance between health and illness in psychological research. The prominence of terms such as “depression”, “anxiety”, and “symptoms of depression magnifies the commitment in the discipline to understanding and addressing mental illnesses. However, juxtaposed against these are positive terms such as “life satisfaction” and “sense of happiness”, suggesting that psychology not only fixates on challenges but also delves deeply into the nuances of positivity and well-being. Furthermore, the significance given to concepts such as “life satisfaction”, “sense of happiness”, and “job satisfaction” underscores an increasing recognition of emotional well-being and job satisfaction as integral to overall mental health. Intertwining the realms of psychology and neuroscience, terms such as “microglial cell activation”, “cognitive impairment”, and “neurodegenerative changes” signal a growing interest in understanding the neural underpinnings of cognitive and psychological phenomena. In addition, the emphasis on “self-efficacy”, “positive emotions”, and “self-esteem” reflect the profound interest in understanding how self-perception and emotions influence human behavior and well-being. Concepts such as “age”, “resilience”, and “creativity” further expand the canvas, showcasing the eclectic and comprehensive nature of inquiries in the field of psychology.
Overall, this analysis paints a vivid picture of modern psychological research, illuminating its multidimensional approach. It demonstrates a discipline that is deeply engaged with both the challenges and triumphs of human existence, offering holistic insight into the human mind and its myriad complexities.
Step 3: Hypothesis generation using link prediction
In the quest to uncover novel causal relationships beyond direct extraction from texts, the technique of link prediction emerges as a pivotal methodology. It hinges on the premise of proposing potential causal ties between concepts that our knowledge graph does not explicitly connect. The process intricately weaves together vector embedding, similarity analysis, and probability-based ranking. Initially, concepts are transposed into a vector space using node2vec, which is valued for its ability to capture topological nuances. Here, every pair of unconnected concepts is assigned a similarity score, and pairs that do not meet a set benchmark are quickly discarded. As we dive deeper into the higher echelons of these scored pairs, the likelihood of their linkage is assessed using the Jaccard similarity of their neighboring concepts. Subsequently, these potential causal relationships are organized in descending order of their derived probabilities, and the elite pairs are selected.
An illustration of this approach is provided in the case highlighted in Figure A1. For instance, the behavioral inhibition system (BIS) exhibits ties to both the behavioral activation system (BAS) and the subsequent behavioral response of the BAS when encountering reward stimuli, termed the BAS reward response. Simultaneously, another concept, interference, finds itself bound to both the BAS and the BAS Reward Response. This configuration hints at a plausible link between the BIS and interference. Such highly probable causal pairs are not mere intellectual curiosity. They act as springboards, catalyzing the genesis of new experimental designs or research hypotheses ripe for empirical probing. In essence, this capability equips researchers with a cutting-edge instrument, empowering them to navigate the unexplored waters of the psychological and neurological domains.
Using pairs of highly probable causal concepts, we pushed GPT-4 to conjure novel causal hypotheses that bridge concepts. To further elucidate the process of this method, Table 4 provides some examples of hypotheses generated from the process. Such hypotheses, as exemplified in the last row, underscore the potential and power of our method for generating innovative causal propositions.
Hypotheses evaluation and results
In this section, we present an analysis focusing on quality in terms of novelty and usefulness of the hypotheses generated. According to existing literature, these dimensions are instrumental in encapsulating the essence of inventive ideas (Boden, 2009 ; McCarthy et al., 2018 ; Miron-Spektor and Beenen, 2015 ). These parameters have not only been quintessential for gauging creative concepts, but they have also been adopted to evaluate the caliber of research hypotheses (Dowling and Lucey, 2023 ; Krenn and Zeilinger, 2020 ; Oleinik, 2019 ). Specifically, we evaluate the quality of the hypotheses generated by the proposed LLMCG algorithm in relation to those generated by PhD students from an elite university who represent human junior experts, the LLM model, which represents advanced AI systems, and the research ideas refined by psychological researchers which represents cooperation between AI and humans.
The evaluation comprises three main stages. In the first stage, the hypotheses are generated by all contributors, including steps taken to ensure fairness and relevance for comparative analysis. In the second stage, the hypotheses from the first stage are independently and blindly reviewed by experts who represent the human academic community. These experts are asked to provide hypothesis ratings using a specially designed questionnaire to ensure statistical validity. The third stage delves deeper by transforming each research idea into the semantic space of a bidirectional encoder representation from transformers (BERT) (Lee et al., 2023 ), allowing us to intricately analyze the intrinsic reasons behind the rating disparities among the groups. This semantic mapping not only pinpoints the nuanced differences, but also provides potential insights into the cognitive constructs of each hypothesis.
Evaluation procedure
Selection of the focus area for hypothesis generation.
Selecting an appropriate focus area for hypothesis generation is crucial to ensure a balanced and insightful comparison of the hypothesis generation capacities between various contributors. In this study, our goal is to gauge the quality of hypotheses derived from four distinct contributors, with measures in place to mitigate potential confounding variables that might skew the results among groups (Rubin, 2005 ). Our choice of domain is informed by two pivotal criteria: the intricacy and subtlety of the subject matter and familiarity with the domain. It is essential that our chosen domain boasts sufficient complexity to prompt meaningful hypothesis generation and offer a robust assessment of both AI and human contributors” depth of understanding and creativity. Furthermore, while human contributors should be well-acquainted with the domain, their expertise need not match the vast corpus knowledge of the AI.
In terms of overarching human pursuits such as the search for happiness, positive psychology distinguishes itself by avoiding narrowly defined, individual-centric challenges (Seligman and Csikszentmihalyi, 2000 ). This alignment with our selection criteria is epitomized by well-being, a salient concept within positive psychology, as shown in Table 3 . Well-being, with its multidimensional essence that encompass emotional, psychological, and social facets, and its central stature in both research and practical applications of positive psychology (Diener et al., 2010 ; Fredrickson, 2001 ; Seligman and Csikszentmihalyi, 2000 ), becomes the linchpin of our evaluation. The growing importance of well-being in the current global context offers myriad novel avenues for hypothesis generation and theoretical advancement (Forgeard et al., 2011 ; Madill et al., 2022 ; Otu et al., 2020 ). Adding to our rationale, the Positive Psychology Research Center at Tsinghua University is a globally renowned hub for cutting-edge research in this domain. Leveraging this stature, we secured participation from specialized Ph.D. students, reinforcing positive psychology as the most fitting domain for our inquiry.
Hypotheses comparison
In our study, the generated psychological hypotheses were categorized into four distinct groups, consisting of two experimental groups and two control groups. The experimental groups encapsulate hypotheses generated by our algorithm, either through random selection or handpicking by experts from a pool of generated hypotheses. On the other hand, control groups comprise research ideas that were meticulously crafted by doctoral students with substantial academic expertise in the domains and hypotheses generated by representative LLMs. In the following, we elucidate the methodology and underlying rationale for each group:
LLMCG algorithm output (Random-selected LLMCG)
Following the requirement of generating hypotheses centred on well-being, the LLMCG algorithm crafted 130 unique hypotheses. These hypotheses were derived by LLMCG’s evaluation of the most likely causal relationships related to well-being that had not been previously documented in research literature datasets. From this refined pool, 30 research ideas were chosen at random for this experimental group. These hypotheses represent the algorithm’s ability to identify causal relationships and formulate pertinent hypotheses.
LLMCG expert-vetted hypotheses (Expert-selected LLMCG)
For this group, two seasoned psychological researchers, one male aged 47 and one female aged 46, in-depth expertise in the realm of Positive Psychology, conscientiously handpicked 30 of the most promising hypotheses from the refined pool, excluding those from the Random-selected LLMCG category. The selection criteria centered on a holistic understanding of both the novelty and practical relevance of each hypothesis. With an illustrious postdoctoral journey and a robust portfolio of publications in positive psychology to their names, they rigorously sifted through the hypotheses, pinpointing those that showcased a perfect confluence of originality and actionable insight. These hypotheses were meticulously appraised for their relevance, structural coherence, and potential academic value, representing the nexus of machine intelligence and seasoned human discernment.
PhD students’ output (Control-Human)
We enlisted the expertise of 16 doctoral students from the Positive Psychology Research Center at Tsinghua University. Under the guidance of their supervisor, each student was provided with a questionnaire geared toward research on well-being. The participants were given a period of four working days to complete and return the questionnaire, which was distributed during vacation to ensure minimal external disruptions and commitments. The specific instructions provided in the questionnaire is detailed in Table B1 , and each participant was asked to complete 3–4 research hypotheses. By the stipulated deadline, we received responses from 13 doctoral students, with a mean age of 31.92 years (SD = 7.75 years), cumulatively presenting 41 hypotheses related to well-being. To maintain uniformity with the other groups, a random selection was made to shortlist 30 hypotheses for further analysis. These hypotheses reflect the integration of core theoretical concepts with the latest insights into the domain, presenting an academic interpretation rooted in their rigorous training and education. Including this group in our study not only provides a natural benchmark for human ingenuity and expertise but also underscores the invaluable contribution of human cognition in research ideation, serving as a pivotal contrast to AI-generated hypotheses. This juxtaposition illuminates the nuanced differences between human intellectual depth and AI’s analytical progress, enriching the comparative dimensions of our study.
Claude model output (Control-Claude)
This group exemplifies the pinnacle of current LLM technology in generating research hypotheses. Since LLMCG is a nascent technology, its assessment requires a comparative study with well-established counterparts, creating a key paradigm in comparative research. Currently, Claude-2 and GPT-4 represent the apex of AI technology. For example, Claude-2, with an accuracy rate of 54. 4% excels in reasoning and answering questions, substantially outperforming other models such as Falcon, Koala and Vicuna, which have accuracy rates of 17.1–25.5% (Wu et al., 2023 ). To facilitate a more comprehensive evaluation of the new model by researchers and to increase the diversity and breadth of comparison, we chose Claude-2 as the control model. Using the detailed instructions provided in Table B2, Claude-2 was iteratively prompted to generate research hypotheses, generating ten hypotheses per prompt, culminating in a total of 50 hypotheses. Although the sheer number and range of these hypotheses accentuate the capabilities of Claude-2, to ensure compatibility in terms of complexity and depth between all groups, a subsequent refinement was considered essential. With minimal human intervention, GPT-4 was used to evaluate these 50 hypotheses and select the top 30 that exhibited the most innovative, relevant, and academically valuable insights. This process ensured the infusion of both the LLM”s analytical prowess and a layer of qualitative rigor, thus giving rise to a set of hypotheses that not only align with the overarching theme of well-being but also resonate with current academic discourse.
Hypotheses assessment
The assessment of the hypotheses encompasses two key components: the evaluation conducted by eminent psychology professors emphasizing novelty and utility, and the deep semantic analysis involving BERT and t -distributed stochastic neighbor embedding ( t -SNE) visualization to discern semantic structures and disparities among hypotheses.
Human academic community
The review task was entrusted to three eminent psychology professors (all male, mean age = 42.33), who have a decade-long legacy in guiding doctoral and master”s students in positive psychology and editorial stints in renowned journals; their task was to conduct a meticulous evaluation of the 120 hypotheses. Importantly, to ensure unbiased evaluation, the hypotheses were presented to them in a completely randomized order in the questionnaire.
Our emphasis was undeniably anchored to two primary tenets: novelty and utility (Cohen, 2017 ; Shardlow et al., 2018 ; Thompson and Skau, 2023 ; Yu et al., 2016 ), as shown in Table B3 . Utility in hypothesis crafting demands that our propositions extend beyond mere factual accuracy; they must resonate deeply with academic investigations, ensuring substantial practical implications. Given the inherent challenges of research, marked by constraints in time, manpower, and funding, it is essential to design hypotheses that optimize the utilization of these resources. On the novelty front, we strive to introduce innovative perspectives that have the power to challenge and expand upon existing academic theories. This not only propels the discipline forward but also ensures that we do not inadvertently tread on ground already covered by our contemporaries.
Deep semantic analysis
While human evaluations provide invaluable insight into the novelty and utility of hypotheses, to objectively discern and visualize semantic structures and the disparities among them, we turn to the realm of deep learning. Specifically, we employ the power of BERT (Devlin et al., 2018 ). BERT, as highlighted by Lee et al. ( 2023 ), had a remarkable potential to assess the innovation of ideas. By translating each hypothesis into a high-dimensional vector in the BERT domain, we obtain the profound semantic core of each statement. However, such granularity in dimensions presents challenges when aiming for visualization.
To alleviate this and to intuitively understand the clustering and dispersion of these hypotheses in semantic space, we deploy the t -SNE ( t -distributed Stochastic Neighbor Embedding) technique (Van der Maaten and Hinton, 2008 ), which is adept at reducing the dimensionality of the data while preserving the relative pairwise distances between the items. Thus, when we map our BERT-encoded hypotheses onto a 2D t -SNE plane, an immediate visual grasp on how closely or distantly related our hypotheses are in terms of their semantic content. Our intent is twofold: to understand the semantic terrains carved out by the different groups and to infer the potential reasons for some of the hypotheses garnered heightened novelty or utility ratings from experts. The convergence of human evaluations and semantic layouts, as delineated by Algorithm 1 in Appendix B , reveal the interplay between human intuition and the inherent semantic structure of the hypotheses.
Qualitative analysis by topic analysis
To better understand the underlying thought processes and the topical emphasis of both PhD students and the LLMCG model, qualitative analyses were performed using visual tools such as word clouds and connection graphs, as detailed in Appendix B . The word cloud, as a graphical representation, effectively captures the frequency and importance of terms, providing direct visualization of the dominant themes. Connection graphs, on the other hand, elucidate the relationships and interplay between various themes and concepts. Using these visual tools, we aimed to achieve a more intuitive and clear representation of the data, allowing for easy comparison and interpretation.
Observations drawn from both the word clouds and the connection graphs in Figures B1 and B2 provide us with a rich tapestry of insights into the thought processes and priorities of Ph.D. students and the LLMCG model. For instance, the emphasis in the Control-Human word cloud on terms such as “robot” and “AI” indicates a strong interest among Ph.D. students in the nexus between technology and psychology. It is particularly fascinating to see a group of academically trained individuals focusing on the real world implications and intersections of their studies, as shown by their apparent draw toward trending topics. This not only underscores their adaptability but also emphasizes the importance of contextual relevance. Conversely, the LLMCG groups, particularly the Expert-selected LLMCG group, emphasize the community, collective experiences, and the nuances of social interconnectedness. This denotes a deep-rooted understanding and application of higher-order social psychological concepts, reflecting the model”s ability to dive deep into the intricate layers of human social behavior.
Furthermore, the connection graphs support these observations. The Control-Human graph, with its exploration of themes such as “Robot Companionship” and its relation to factors such as “heart rate variability (HRV)”, demonstrates a confluence of technology and human well-being. The other groups, especially the Random-selected LLMCG group, yield themes that are more societal and structural, hinting at broader determinants of individual well-being.
Analysis of human evaluations
To quantify the agreement among the raters, we employed Spearman correlation coefficients. The results, as shown in Table B5, reveal a spectrum of agreement levels between the reviewer pairs, showcasing the subjective dimension intrinsic to the evaluation of novelty and usefulness. In particular, the correlation between reviewer 1 and reviewer 2 in novelty (Spearman r = 0.387, p < 0.0001) and between reviewer 2 and reviewer 3 in usefulness (Spearman r = 0.376, p < 0.0001) suggests a meaningful level of consensus, particularly highlighting their capacity to identify valuable insights when evaluating hypotheses.
The variations in correlation values, such as between reviewer 2 and reviewer 3 ( r = 0.069, p = 0.453), can be attributed to the diverse research orientations and backgrounds of each reviewer. Reviewer 1 focuses on social ecology, reviewer 3 specializes in neuroscientific methodologies, and reviewer 2 integrates various views using technologies like virtual reality, and computational methods. In our evaluation, we present specific hypotheses cases to illustrate the differing perspectives between reviewers, as detailed in Table B4 and Figure B3. For example, C5 introduces the novel concept of “Virtual Resilience”. Reviewers 1 and 3 highlighted its originality and utility, while reviewer 2 rated it lower in both categories. Meanwhile, C6, which focuses on social neuroscience, resonated with reviewer 3, while reviewers 1 and 2 only partially affirmed it. These differences underscore the complexity of evaluating scientific contributions and highlight the importance of considering a range of expert opinions for a comprehensive evaluation.
This assessment is divided into two main sections: Novelty analysis and usefulness analysis.
Novelty analysis
In the dynamic realm of scientific research, measuring and analyzing novelty is gaining paramount importance (Shin et al., 2022 ). ANOVA was used to analyze the novelty scores represented in Fig. 2 a, and we identified a significant influence of the group factor on the mean novelty score between different reviewers. Initially, z-scores were calculated for each reviewer”s ratings to standardize the scoring scale, which were then averaged. The distinct differences between the groups, as visualized in the boxplots, are statistically underpinned by the results in Table 5 . The ANOVA results revealed a pronounced effect of the grouping factor ( F (3116) = 6.92, p = 0.0002), with variance explained by the grouping factor (R-squared) of 15.19%.
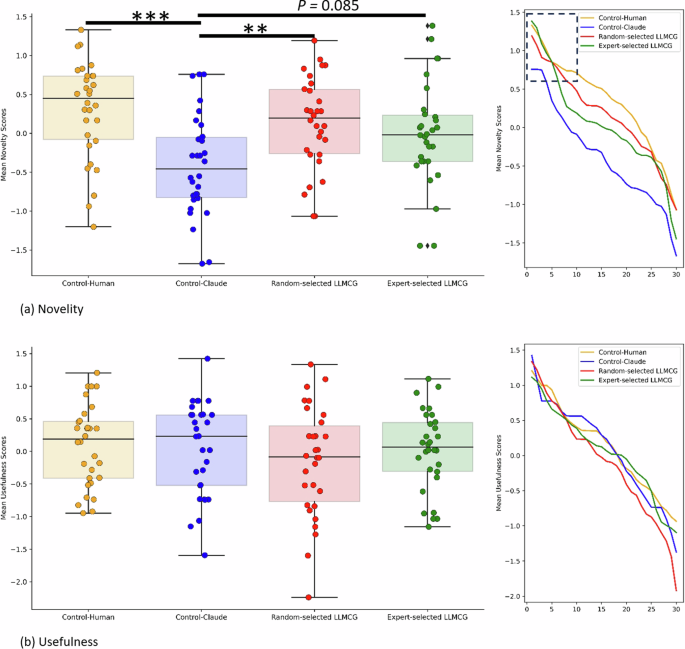
Box plots on the left ( a ) and ( b ) depict distributions of novelty and usefulness scores, respectively, while smoothed line plots on the right demonstrate the descending order of novelty and usefulness scores and subjected to a moving average with a window size of 2. * denotes p < 0.05, ** denotes p <0.01.
Further pairwise comparisons using the Bonferroni method, as delineated in Table 5 and visually corroborated by Fig. 2 a; significant disparities were discerned between Random-selected LLMCG and Control-Claude ( t (59) = 3.34, p = 0.007) and between Control-Human and Control-Claude ( t (59) = 4.32, p < 0.001). The Cohen’s d values of 0.8809 and 1.1192 respectively indicate that the novelty scores for the Random-selected LLMCG and Control-Human groups are significantly higher than those for the Control-Claude group. Additionally, when considering the cumulative distribution plots to the right of Fig. 2 a, we observe the distributional characteristics of the novel scores. For example, it can be observed that the Expert-selected LLMCG curve portrays a greater concentration in the middle score range when compared to the Control-Claude , curve but dominates in the high novelty scores (highlighted in dashed rectangle). Moreover, comparisons involving Control-Human with both Random-selected LLMCG and Expert-selected LLMCG did not manifest statistically significant variances, indicating aligned novelty perceptions among these groups. Finally, the comparisons between Expert-selected LLMCG and Control-Claude ( t (59) = 2.49, p = 0.085) suggest a trend toward significance, with a Cohen’s d value of 0.6226 indicating generally higher novelty scores for Expert-selected LLMCG compared to Control-Claude .
To mitigate potential biases due to individual reviewer inclinations, we expanded our evaluation to include both median and maximum z-scores from the three reviewers for each hypothesis. These multifaceted analyses enhance the robustness of our results by minimizing the influence of extreme values and potential outliers. First, when analyzing the median novelty scores, the ANOVA test demonstrated a notable association with the grouping factor ( F (3,116) = 6.54, p = 0.0004), which explained 14.41% of the variance. As illustrated in Table 5 , pairwise evaluations revealed significant disparities between Control-Human and Control-Claude ( t (59) = 4.01, p = 0.001), with Control-Human performing significantly higher than Control-Claude (Cohen’s d = 1.1031). Similarly, there were significant differences between Random-selected LLMCG and Control-Claude ( t (59) = 3.40, p = 0.006), where Random-selected LLMCG also significantly outperformed Control-Claude (Cohen’s d = 0.8875). Interestingly, the comparison of Expert-selected LLMCG with Control-Claude ( t (59) = 1.70, p = 0.550) and other group pairings did not include statistically significant differences.
Subsequently, turning our attention to maximum novelty scores provided crucial insights, especially where outlier scores may carry significant weight. The influence of the grouping factor was evident ( F (3,116) = 7.20, p = 0.0002), indicating an explained variance of 15.70%. In particular, clear differences emerged between Control-Human and Control-Claude ( t (59) = 4.36, p < 0.001), and between Random-selected LLMCG and Control-Claude ( t (59) = 3.47, p = 0.004). A particularly intriguing observation was the significant difference between Expert-selected LLMCG and Control-Claude ( t (59) = 3.12, p = 0.014). The Cohen’s d values of 1.1637, 1.0457, and 0.6987 respectively indicate that the novelty scores for the Control-Human , Random-selected LLMCG , and Expert-selected LLMCG groups are significantly higher than those for the Control-Claude group. Together, these analyses offer a multifaceted perspective on novelty evaluations. Specifically, the results of the median analysis echo and support those of the mean, reinforcing the reliability of our assessments. The discerned significance between Control-Claude and Expert-selected LLMCG in the median data emphasizes the intricate differences, while also pointing to broader congruence in novelty perceptions.
Usefulness analysis
Evaluating the practical impact of hypotheses is crucial in scientific research assessments. In the mean useful spectrum, the grouping factor did not exert a significant influence ( F (3,116) = 5.25, p = 0.553). Figure 2 b presents the utility score distributions between groups. The narrow interquartile range of Control-Human suggests a relatively consistent assessment among reviewers. On the other hand, the spread and outliers in the Control-Claude distribution hint at varied utility perceptions. Both LLMCG groups cover a broad score range, demonstrating a mixture of high and low utility scores, while the Expert-selected LLMCG gravitates more toward higher usefulness scores. The smoothed line plots accompanying Fig. 2 b further detail the score densities. For instance, Random-selected LLMCG boasts several high utility scores, counterbalanced by a smattering of low scores. Interestingly, the distributions for Control-Human and Expert-selected LLMCG appear to be closely aligned. While mean utility scores provide an overarching view, the nuances within the boxplots and smoothed plots offer deeper insights. This comprehensive understanding can guide future endeavors in content generation and evaluation, spotlighting key areas of focus and potential improvements.
Comparison between the LLMCG and GPT-4
To evaluate the impact of integrating a causal graph with GPT-4, we performed an ablation study comparing the hypotheses generated by GPT-4 alone and those of the proposed LLMCG framework. For this experiment, 60 hypotheses were created using GPT-4, following the detailed instructions in Table B2 . Furthermore, 60 hypotheses for the LLMCG group were randomly selected from the remaining pool of 70 hypotheses. Subsequently, both sets of hypotheses were assessed by three independent reviewers for novelty and usefulness, as previously described.
Table 6 shows a comparison between the GPT-4 and LLMCG groups, highlighting a significant difference in novelty scores (mean value: t (119) = 6.60, p < 0.0001) but not in usefulness scores (mean value: t (119) = 1.31, p = 0.1937). This indicates that the LLMCG framework significantly enhances hypothesis novelty (all Cohen’s d > 1.1) without affecting usefulness compared to the GPT-4 group. Figure B6 visually contrasts these findings, underlining the causal graph’s unique role in fostering novel hypothesis generation when integrated with GPT-4.
The t -SNE visualizations (Fig. 3 ) illustrate the semantic relationships between different groups, capturing the patterns of novelty and usefulness. Notably, a distinct clustering among PhD students suggests shared academic influences, while the LLMCG groups display broader topic dispersion, hinting at a wider semantic understanding. The size of the bubbles reflects the novelty and usefulness scores, emphasizing the diverse perceptions of what is considered innovative versus beneficial. Additionally, the numbers near the yellow dots represent the participant IDs, which demonstrated that the semantics of the same participant, such as H05 or H06, are closely aligned. In Fig. B4 , a distinct clustering of examples is observed, particularly highlighting the close proximity of hypotheses C3, C4, and C8 within the semantic space. This observation is further elucidated in Appendix B , enhancing the comprehension of BERT’s semantic representation. Instead of solely depending on superficial textual descriptions, this analysis penetrates into the underlying understanding of concepts within the semantic space, a topic also explored in recent research (Johnson et al., 2023 ).
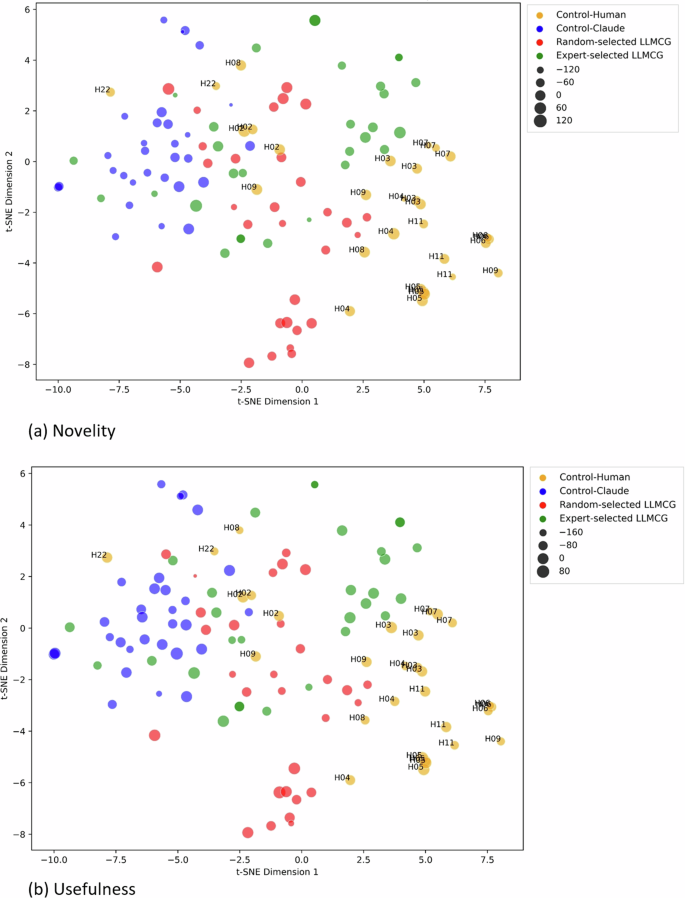
Comparison of ( a ) novelty and ( b ) usefulness scores (bubble size scaled by 100) among the different groups.
In the distribution of semantic distances (Fig. 4 ), we observed that the Control-Human group exhibits a distinctively greater semantic distance in comparison to the other groups, emphasizing their unique semantic orientations. The statistical support for this observation is derived from the ANOVA results, with a significant F-statistic ( F (3,1652) = 84.1611, p < 0.00001), underscoring the impact of the grouping factor. This factor explains a remarkable 86.96% of the variance, as indicated by the R -squared value. Multiple comparisons, as shown in Table 7 , further elucidate the subtleties of these group differences. Control-Human and Control-Claude exhibit a significant contrast in their semantic distances, as highlighted by the t value of 16.41 and the adjusted p value ( < 0.0001). This difference indicates distinct thought patterns or emphasis in the two groups. Notably, Control-Human demonstrates a greater semantic distance (Cohen’s d = 1.1630). Similarly, a comparison of the Control-Claude and LLMCG models reveals pronounced differences (Cohen’s d > 0.9), more so with the Expert-selected LLMCG ( p < 0.0001). A comparison of Control-Human with the LLMCG models shows divergent semantic orientations, with statistically significant larger distances than Random-selected LLMCG ( p = 0.0036) and a trend toward difference with Expert-selected LLMCG ( p = 0.0687). Intriguingly, the two LLMCG groups—Random-selected and Expert-selected—exhibit similar semantic distances, as evidenced by a nonsignificant p value of 0.4362. Furthermore, the significant distinctions we observed, particularly between the Control-Human and other groups, align with human evaluations of novelty. This coherence indicates that the BERT space representation coupled with statistical analyses could effectively mimic human judgment. Such results underscore the potential of this approach for automated hypothesis testing, paving the way for more efficient and streamlined semantic evaluations in the future.
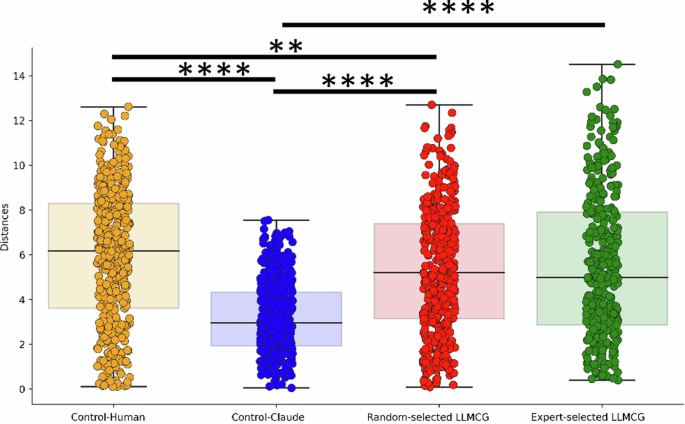
Note: ** denotes p < 0.01, **** denotes p < 0.0001.
In general, visual and statistical analyses reveal the nuanced semantic landscapes of each group. While the Ph.D. students’ shared background influences their clustering, the machine models exhibit a comprehensive grasp of topics, emphasizing the intricate interplay of individual experiences, academic influences, and algorithmic understanding in shaping semantic representations.
This investigation carried out a detailed evaluation of the various hypothesis contributors, blending both quantitative and qualitative analyses. In terms of topic analysis, distinct variations were observed between Control-Human and LLMCG, the latter presenting more expansive thematic coverage. For human evaluation, hypotheses from Ph.D. students paralleled the LLMCG in novelty, reinforcing AI’s growing competence in mirroring human innovative thinking. Furthermore, when juxtaposed with AI models such as Control-Claude , the LLMCG exhibited increased novelty. Deep semantic analysis via t -SNE and BERT representations allowed us to intuitively grasp semantic essence of hypotheses, signaling the possibility of future automated hypothesis assessments. Interestingly, LLMCG appeared to encompass broader complementary domains compared to human input. Taken together, these findings highlight the emerging role of AI in hypothesis generation and provide key insights into hypothesis evaluation across diverse origins.
General discussion
This research delves into the synergistic relationship between LLM and causal graphs in the hypothesis generation process. Our findings underscore the ability of LLM, when integrated with causal graph techniques, to produce meaningful hypotheses with increased efficiency and quality. By centering our investigation on “well-being” we emphasize its pivotal role in psychological studies and highlight the potential convergence of technology and society. A multifaceted assessment approach to evaluate quality by topic analysis, human evaluation and deep semantic analysis demonstrates that AI-augmented methods not only outshine LLM-only techniques in generating hypotheses with superior novelty and show quality on par with human expertise but also boast the capability for more profound conceptual incorporations and a broader semantic spectrum. Such a multifaceted lens of assessment introduces a novel perspective for the scholarly realm, equipping researchers with an enriched understanding and an innovative toolset for hypothesis generation. At its core, the melding of LLM and causal graphs signals a promising frontier, especially in regard to dissecting cornerstone psychological constructs such as “well-being”. This marriage of methodologies, enriched by the comprehensive assessment angle, deepens our comprehension of both the immediate and broader ramifications of our research endeavors.
The prominence of causal graphs in psychology is profound, they offer researchers a unified platform for synthesizing and hypothesizing diverse psychological realms (Borsboom et al., 2021 ; Uleman et al., 2021 ). Our study echoes this, producing groundbreaking hypotheses comparable in depth to early expert propositions. Deep semantic analysis bolstered these findings, emphasizing that our hypotheses have distinct cross-disciplinary merits, particularly when compared to those of individual doctoral scholars. However, the traditional use of causal graphs in psychology presents challenges due to its demanding nature, often requiring insights from multiple experts (Crielaard et al., 2022 ). Our research, however, harnesses LLM’s causal extraction, automating causal pair derivation and, in turn, minimizing the need for extensive expert input. The union of the causal graphs’ systematic approach with AI-driven creativity, as seen with LLMs, paves the way for the future of psychological inquiry. Thanks to advancements in AI, barriers once created by causal graphs’ intricate procedures are being dismantled. Furthermore, as the era of big data dawns, the integration of AI and causal graphs in psychology augments research capabilities, but also brings into focus the broader implications for society. This fusion provides a nuanced understanding of the intricate sociopsychological dynamics, emphasizing the importance of adapting research methodologies in tandem with technological progress.
In the realm of research, LLMs serve a unique purpose, often by acting as the foundation or baseline against which newer methods and approaches are assessed. The demonstrated productivity enhancements by generative AI tools, as evidenced by Noy and Zhang ( 2023 ), indicate the potential of such LLMs. In our investigation, we pit the hypotheses generated by such substantial models against our integrated LLMCG approach. Intriguingly, while these LLMs showcased admirable practicality in their hypotheses, they substantially lagged behind in terms of innovation when juxtaposed with the doctoral student and LLMCG group. This divergence in results can be attributed to the causal network curated from 43k research papers, funneling the vast knowledge reservoir of the LLM squarely into the realm of scientific psychology. The increased precision in hypothesis generation by these models fits well within the framework of generative networks. Tong et al. ( 2021 ) highlighted that, by integrating structured constraints, conventional neural networks can accurately generate semantically relevant content. One of the salient merits of the causal graph, in this context, is its ability to alleviate inherent ambiguity or interpretability challenges posed by LLMs. By providing a systematic and structured framework, the causal graph aids in unearthing the underlying logic and rationale of the outputs generated by LLMs. Notably, this finding echoes the perspective of Pan et al. ( 2023 ), where the integration of structured knowledge from knowledge graphs was shown to provide an invaluable layer of clarity and interpretability to LLMs, especially in complex reasoning tasks. Such structured approaches not only boost the confidence of researchers in the hypotheses derived but also augment the transparency and understandability of LLM outputs. In essence, leveraging causal graphs may very well herald a new era in model interpretability, serving as a conduit to unlock the black box that large models often represent in contemporary research.
In the ever-evolving tapestry of research, every advancement invariably comes with its unique set of constraints, and our study was no exception. On the technical front, a pivotal challenge stemmed from the opaque inner workings of the GPT. Determining the exact machinations within the GPT that lead to the formation of specific causal pairs remains elusive, thereby reintroducing the age-old issue of AI’s inherent lack of transparency (Buruk, 2023 ; Cao and Yousefzadeh, 2023 ). This opacity is magnified in our sparse causal graph, which, while expansive, is occasionally riddled with concepts that, while semantically distinct, converge in meaning. In tangible applications, a careful and meticulous algorithmic evaluation would be imperative to construct an accurate psychological conceptual landscape. Delving into psychology, which bridges humanities and natural sciences, it continuously aims to unravel human cognition and behavior (Hergenhahn and Henley, 2013 ). Despite the dominance of traditional methodologies (Henrich et al., 2010 ; Shah et al., 2015 ), the present data-centric era amplifies the synergy of technology and humanities, resonating with Hasok Chang’s vision of enriched science (Chang, 2007 ). This symbiosis is evident when assessing structural holes in social networks (Burt, 2004 ) and viewing novelty as a bridge across these divides (Foster et al., 2021 ). Such perspectives emphasize the importance of thorough algorithmic assessments, highlighting potential avenues in humanities research, especially when incorporating large language models for innovative hypothesis crafting and verification.
However, there are some limitations to this research. Firstly, we acknowledge that constructing causal relationship graphs has potential inaccuracies, with ~13% relationship pairs not aligning with human expert estimations. Enhancing the estimation of relationship extraction could be a pathway to improve the accuracy of the causal graph, potentially leading to more robust hypotheses. Secondly, our validation process was limited to 130 hypotheses, however, the vastness of our conceptual landscape suggests countless possibilities. As an exemplar, the twenty pivotal psychological concepts highlighted in Table 3 alone could spawn an extensive array of hypotheses. However, the validation of these surrounding hypotheses would unquestionably lead to a multitude of speculations. A striking observation during our validation was the inconsistency in the evaluations of the senior expert panels (as shown in Table B5 ). This shift underscores a pivotal insight: our integration of AI has transitioned the dependency on scarce expert resources from hypothesis generation to evaluation. In the future, rigorous evaluations ensuring both novelty and utility could become a focal point of exploration. The promising path forward necessitates a thoughtful integration of technological innovation and human expertise to fully realize the potential suggested by our study.
In conclusion, our research provides pioneering insight into the symbiotic fusion of LLMs, which are epitomized by GPT, and causal graphs from the realm of psychological hypothesis generation, especially emphasizing “well-being”. Importantly, as highlighted by (Cao and Yousefzadeh, 2023 ), ensuring a synergistic alignment between domain knowledge and AI extrapolation is crucial. This synergy serves as the foundation for maintaining AI models within their conceptual limits, thus bolstering the validity and reliability of the hypotheses generated. Our approach intricately interweaves the advanced capabilities of LLMs with the methodological prowess of causal graphs, thereby optimizing while also refining the depth and precision of hypothesis generation. The causal graph, of paramount importance in psychology due to its cross-disciplinary potential, often demands vast amounts of expert involvement. Our innovative approach addresses this by utilizing LLM’s exceptional causal extraction abilities, effectively facilitating the transition of intense expert engagement from hypothesis creation to evaluation. Therefore, our methodology combined LLM with causal graphs, propelling psychological research forward by improving hypothesis generation and offering tools to blend theoretical and data-centric approaches. This synergy particularly enriches our understanding of social psychology’s complex dynamics, such as happiness research, demonstrating the profound impact of integrating AI with traditional research frameworks.
Data availability
The data generated and analyzed in this study are partially available within the Supplementary materials . For additional data supporting the findings of this research, interested parties may contact the corresponding author, who will provide the information upon receiving a reasonable request.
Battleday RM, Peterson JC, Griffiths TL (2020) Capturing human categorization of natural images by combining deep networks and cognitive models. Nat Commun 11(1):5418
Article ADS PubMed PubMed Central Google Scholar
Bechmann A, Bowker GC (2019) Unsupervised by any other name: hidden layers of knowledge production in artificial intelligence on social media. Big Data Soc 6(1):2053951718819569
Article Google Scholar
Binz M, Schulz E (2023) Using cognitive psychology to understand GPT-3. Proc Natl Acad Sci 120(6):e2218523120
Article CAS PubMed PubMed Central Google Scholar
Boden MA (2009) Computer models of creativity. AI Mag 30(3):23–23
Google Scholar
Borsboom D, Deserno MK, Rhemtulla M, Epskamp S, Fried EI, McNally RJ (2021) Network analysis of multivariate data in psychological science. Nat Rev Methods Prim 1(1):58
Article CAS Google Scholar
Burt RS (2004) Structural holes and good ideas. Am J Sociol 110(2):349–399
Buruk O (2023) Academic writing with GPT-3.5: reflections on practices, efficacy and transparency. arXiv preprint arXiv:2304.11079
Cao X, Yousefzadeh R (2023) Extrapolation and AI transparency: why machine learning models should reveal when they make decisions beyond their training. Big Data Soc 10(1):20539517231169731
Chang H (2007) Scientific progress: beyond foundationalism and coherentism1. R Inst Philos Suppl 61:1–20
Cheng K, Guo Q, He Y, Lu Y, Gu S, Wu H (2023) Exploring the potential of GPT-4 in biomedical engineering: the dawn of a new era. Ann Biomed Eng 51:1645–1653
Article ADS PubMed Google Scholar
Cichy RM, Khosla A, Pantazis D, Torralba A, Oliva A (2016) Comparison of deep neural networks to spatio-temporal cortical dynamics of human visual object recognition reveals hierarchical correspondence. Sci Rep 6(1):27755
Article ADS CAS PubMed PubMed Central Google Scholar
Cohen BA (2017) How should novelty be valued in science? Elife 6:e28699
Article PubMed PubMed Central Google Scholar
Crielaard L, Uleman JF, Châtel BD, Epskamp S, Sloot P, Quax R (2022) Refining the causal loop diagram: a tutorial for maximizing the contribution of domain expertise in computational system dynamics modeling. Psychol Methods 29(1):169–201
Article PubMed Google Scholar
Devlin J, Chang M W, Lee K & Toutanova (2019) Bert: pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers) (pp. 4171–4186)
Diener E, Wirtz D, Tov W, Kim-Prieto C, Choi D-W, Oishi S, Biswas-Diener R (2010) New well-being measures: short scales to assess flourishing and positive and negative feelings. Soc Indic Res 97:143–156
Dowling M, Lucey B (2023) ChatGPT for (finance) research: the Bananarama conjecture. Financ Res Lett 53:103662
Forgeard MJ, Jayawickreme E, Kern ML, Seligman ME (2011) Doing the right thing: measuring wellbeing for public policy. Int J Wellbeing 1(1):79–106
Foster J G, Shi F & Evans J (2021) Surprise! Measuring novelty as expectation violation. SocArXiv
Fredrickson BL (2001) The role of positive emotions in positive psychology: The broaden-and-build theory of positive emotions. Am Psychol 56(3):218
Gu Q, Kuwajerwala A, Morin S, Jatavallabhula K M, Sen B, Agarwal, A et al. (2024) ConceptGraphs: open-vocabulary 3D scene graphs for perception and planning. In 2nd Workshop on Language and Robot Learning: Language as Grounding
Henrich J, Heine SJ, Norenzayan A (2010) Most people are not WEIRD. Nature 466(7302):29–29
Article ADS CAS PubMed Google Scholar
Hergenhahn B R, Henley T (2013) An introduction to the history of psychology . Cengage Learning
Jaccard J, Jacoby J (2019) Theory construction and model-building skills: a practical guide for social scientists . Guilford publications
Johnson DR, Kaufman JC, Baker BS, Patterson JD, Barbot B, Green AE (2023) Divergent semantic integration (DSI): Extracting creativity from narratives with distributional semantic modeling. Behav Res Methods 55(7):3726–3759
Kıcıman E, Ness R, Sharma A & Tan C (2023) Causal reasoning and large language models: opening a new frontier for causality. arXiv preprint arXiv:2305.00050
Koehler DJ (1994) Hypothesis generation and confidence in judgment. J Exp Psychol Learn Mem Cogn 20(2):461–469
Krenn M, Zeilinger A (2020) Predicting research trends with semantic and neural networks with an application in quantum physics. Proc Natl Acad Sci 117(4):1910–1916
Lee H, Zhou W, Bai H, Meng W, Zeng T, Peng K & Kumada T (2023) Natural language processing algorithms for divergent thinking assessment. In: Proc IEEE 6th Eurasian Conference on Educational Innovation (ECEI) p 198–202
Madill A, Shloim N, Brown B, Hugh-Jones S, Plastow J, Setiyawati D (2022) Mainstreaming global mental health: Is there potential to embed psychosocial well-being impact in all global challenges research? Appl Psychol Health Well-Being 14(4):1291–1313
McCarthy M, Chen CC, McNamee RC (2018) Novelty and usefulness trade-off: cultural cognitive differences and creative idea evaluation. J Cross-Cult Psychol 49(2):171–198
McGuire WJ (1973) The yin and yang of progress in social psychology: seven koan. J Personal Soc Psychol 26(3):446–456
Miron-Spektor E, Beenen G (2015) Motivating creativity: The effects of sequential and simultaneous learning and performance achievement goals on product novelty and usefulness. Organ Behav Hum Decis Process 127:53–65
Nisbett RE, Peng K, Choi I, Norenzayan A (2001) Culture and systems of thought: holistic versus analytic cognition. Psychol Rev 108(2):291–310
Article CAS PubMed Google Scholar
Noy S, Zhang W (2023) Experimental evidence on the productivity effects of generative artificial intelligence. Science 381:187–192
Oleinik A (2019) What are neural networks not good at? On artificial creativity. Big Data Soc 6(1):2053951719839433
Otu A, Charles CH, Yaya S (2020) Mental health and psychosocial well-being during the COVID-19 pandemic: the invisible elephant in the room. Int J Ment Health Syst 14:1–5
Pan S, Luo L, Wang Y, Chen C, Wang J & Wu X (2024) Unifying large language models and knowledge graphs: a roadmap. IEEE Transactions on Knowledge and Data Engineering 36(7):3580–3599
Rubin DB (2005) Causal inference using potential outcomes: design, modeling, decisions. J Am Stat Assoc 100(469):322–331
Article MathSciNet CAS Google Scholar
Sanderson K (2023) GPT-4 is here: what scientists think. Nature 615(7954):773
Seligman ME, Csikszentmihalyi M (2000) Positive psychology: an introduction. Am Psychol 55(1):5–14
Shah DV, Cappella JN, Neuman WR (2015) Big data, digital media, and computational social science: possibilities and perils. Ann Am Acad Political Soc Sci 659(1):6–13
Shardlow M, Batista-Navarro R, Thompson P, Nawaz R, McNaught J, Ananiadou S (2018) Identification of research hypotheses and new knowledge from scientific literature. BMC Med Inform Decis Mak 18(1):1–13
Shin H, Kim K, Kogler DF (2022) Scientific collaboration, research funding, and novelty in scientific knowledge. PLoS ONE 17(7):e0271678
Thomas RP, Dougherty MR, Sprenger AM, Harbison J (2008) Diagnostic hypothesis generation and human judgment. Psychol Rev 115(1):155–185
Thomer AK, Wickett KM (2020) Relational data paradigms: what do we learn by taking the materiality of databases seriously? Big Data Soc 7(1):2053951720934838
Thompson WH, Skau S (2023) On the scope of scientific hypotheses. R Soc Open Sci 10(8):230607
Tong S, Liang X, Kumada T, Iwaki S (2021) Putative ratios of facial attractiveness in a deep neural network. Vis Res 178:86–99
Uleman JF, Melis RJ, Quax R, van der Zee EA, Thijssen D, Dresler M (2021) Mapping the multicausality of Alzheimer’s disease through group model building. GeroScience 43:829–843
Van der Maaten L, Hinton G (2008) Visualizing data using t-SNE. J Mach Learn Res 9(11):2579–2605
Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez A N & Polosukhin I (2017) Attention is all you need. In Advances in Neural Information Processing Systems
Wang H, Fu T, Du Y, Gao W, Huang K, Liu Z (2023) Scientific discovery in the age of artificial intelligence. Nature 620(7972):47–60
Webber J (2012) A programmatic introduction to neo4j. In Proceedings of the 3rd annual conference on systems, programming, and applications: software for humanity p 217–218
Williams K, Berman G, Michalska S (2023) Investigating hybridity in artificial intelligence research. Big Data Soc 10(2):20539517231180577
Wu S, Koo M, Blum L, Black A, Kao L, Scalzo F & Kurtz I (2023) A comparative study of open-source large language models, GPT-4 and Claude 2: multiple-choice test taking in nephrology. arXiv preprint arXiv:2308.04709
Yu F, Peng T, Peng K, Zheng SX, Liu Z (2016) The Semantic Network Model of creativity: analysis of online social media data. Creat Res J 28(3):268–274
Download references
Acknowledgements
The authors thank Dr. Honghong Bai (Radboud University), Dr. ChienTe Wu (The University of Tokyo), Dr. Peng Cheng (Tsinghua University), and Yusong Guo (Tsinghua University) for their great comments on the earlier version of this manuscript. This research has been generously funded by personal contributions, with special acknowledgment to K. Mao. Additionally, he conceived and developed the causality graph and AI hypothesis generation technology presented in this paper from scratch, and generated all AI hypotheses and paid for its costs. The authors sincerely thank K. Mao for his support, which enabled this research. In addition, K. Peng and S. Tong were partly supported by the Tsinghua University lnitiative Scientific Research Program (No. 20213080008), Self-Funded Project of Institute for Global Industry, Tsinghua University (202-296-001), Shuimu Scholars program of Tsinghua University (No. 2021SM157), and the China Postdoctoral International Exchange Program (No. YJ20210266).
Author information
These authors contributed equally: Song Tong, Kai Mao.
Authors and Affiliations
Department of Psychological and Cognitive Sciences, Tsinghua University, Beijing, China
Song Tong & Kaiping Peng
Positive Psychology Research Center, School of Social Sciences, Tsinghua University, Beijing, China
Song Tong, Zhen Huang, Yukun Zhao & Kaiping Peng
AI for Wellbeing Lab, Tsinghua University, Beijing, China
Institute for Global Industry, Tsinghua University, Beijing, China
Kindom KK, Tokyo, Japan
You can also search for this author in PubMed Google Scholar
Contributions
Song Tong: Data analysis, Experiments, Writing—original draft & review. Kai Mao: Designed the causality graph methodology, Generated AI hypotheses, Developed hypothesis generation techniques, Writing—review & editing. Zhen Huang: Statistical Analysis, Experiments, Writing—review & editing. Yukun Zhao: Conceptualization, Project administration, Supervision, Writing—review & editing. Kaiping Peng: Conceptualization, Writing—review & editing.
Corresponding authors
Correspondence to Yukun Zhao or Kaiping Peng .
Ethics declarations
Competing interests.
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Ethical approval
In this study, ethical approval was granted by the Institutional Review Board (IRB) of the Department of Psychology at Tsinghua University, China. The Research Ethics Committee documented this approval under the number IRB202306, following an extensive review that concluded on March 12, 2023. This approval indicates the research’s strict compliance with the IRB’s guidelines and regulations, ensuring ethical integrity and adherence throughout the study.
Informed consent
Before participating, all study participants gave their informed consent. They received comprehensive details about the study’s goals, methods, potential risks and benefits, confidentiality safeguards, and their rights as participants. This process guaranteed that participants were fully informed about the study’s nature and voluntarily agreed to participate, free from coercion or undue influence.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplemental material, rights and permissions.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .
Reprints and permissions
About this article
Cite this article.
Tong, S., Mao, K., Huang, Z. et al. Automating psychological hypothesis generation with AI: when large language models meet causal graph. Humanit Soc Sci Commun 11 , 896 (2024). https://doi.org/10.1057/s41599-024-03407-5
Download citation
Received : 08 November 2023
Accepted : 25 June 2024
Published : 09 July 2024
DOI : https://doi.org/10.1057/s41599-024-03407-5
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
Quick links
- Explore articles by subject
- Guide to authors
- Editorial policies

- Advanced Search
Selecting reliable instances based on evidence theory for transfer learning
New citation alert added.
This alert has been successfully added and will be sent to:
You will be notified whenever a record that you have chosen has been cited.
To manage your alert preferences, click on the button below.
New Citation Alert!
Please log in to your account
Information & Contributors
Bibliometrics & citations, view options, recommendations, integrating priors into domain adaptation based on evidence theory.
Domain adaptation aims to build up a learning model for target domain by leveraging transferable knowledge from different but related source domains. Existing domain adaptation methods generally transfer the knowledge from source domain to target domain ...
A Survey on Transfer Learning
A major assumption in many machine learning and data mining algorithms is that the training and future data must be in the same feature space and have the same distribution. However, in many real-world applications, this assumption may not hold. For ...
Deep autoencoder based domain adaptation for transfer learning
The concept of transfer learning has received a great deal of concern and interest throughout the last decade. Selecting an ideal representational framework for instances of various domains to minimize the divergence among source and target ...
Information
Published in.
Pergamon Press, Inc.
United States
Publication History
Author tags.
- Machine Learning
- Transfer learning
- Evidence theory
- Dempster-Shafer theory
- Belief functions
- Research-article
Contributors
Other metrics, bibliometrics, article metrics.
- 0 Total Citations
- 0 Total Downloads
- Downloads (Last 12 months) 0
- Downloads (Last 6 weeks) 0
View options
Login options.
Check if you have access through your login credentials or your institution to get full access on this article.
Full Access
Share this publication link.
Copying failed.
Share on social media
Affiliations, export citations.
- Please download or close your previous search result export first before starting a new bulk export. Preview is not available. By clicking download, a status dialog will open to start the export process. The process may take a few minutes but once it finishes a file will be downloadable from your browser. You may continue to browse the DL while the export process is in progress. Download
- Download citation
- Copy citation
We are preparing your search results for download ...
We will inform you here when the file is ready.
Your file of search results citations is now ready.
Your search export query has expired. Please try again.

IMAGES
VIDEO
COMMENTS
Learn the concept and role of hypothesis in machine learning, a model's presumption regarding the connection between input features and output. Explore the hypothesis space, representation, evaluation, testing, and generalization in different algorithms and techniques.
Learn the difference between a hypothesis in science, in statistics, and in machine learning. A hypothesis in machine learning is a candidate model that approximates a target function for mapping inputs to outputs.
Learn what is hypothesis in machine learning, how it differs from model, and how it is used in supervised learning algorithms. Also, compare hypothesis in machine learning with hypothesis in statistics and understand the concepts of null, alternative, significance level, and p-value.
Hypothesis Functions. In the context of machine learning, a hypothesis function, also referred to as a model, is a function that maps inputs to predictions. These predictions are made based on the input data, and if the hypothesis function is well-chosen, these predictions should be close to the actual targets.
In machine learning, a hypothesis is a mathematical function or model that converts input data into output predictions. The model's first belief or explanation is based on the facts supplied. The hypothesis is typically expressed as a collection of parameters characterizing the behavior of the model. If we're building a model to predict the ...
Foundations Of Machine Learning (Free) ... Science - I(Free) SQL for Data Science - II(Free) SQL for Data Science - III(Free) SQL for Data Science - Window Functions(Free) Machine Learning Expert; ... P-value is greater than ($α$) 0.05: the results are not statistically significant, and they don't reject the null hypothesis ...
In machine learning, the term 'hypothesis' can refer to two things. First, it can refer to the hypothesis space, the set of all possible training examples that could be used to predict or answer a new instance. Second, it can refer to the traditional null and alternative hypotheses from statistics. Since machine learning works so closely ...
In the last few lessons, we saw the machine learning process by being introduced to decision trees. We saw that our machine learning process was to gather our training data, train a model to find a hypothesis function, and then use that hypothesis function to make predictions.
The hypothesis formula in machine learning: y= mx b. Where, y is range. m changes in y divided by change in x. x is domain. b is intercept. The purpose of restricting hypothesis space in machine learning is so that these can fit well with the general data that is needed by the user. It checks the reality or deception of observations or inputs ...
Hypothesis. A statistical hypothesis is:. a proposed explanation for an observation. testable on the basis of observed groups of random variables. Null Hypothesis. The Null Hypothesis is position that there is no relationship between two measured groups.. An example is the development of a new pharmaceutical drug, where the Null Hypothesis is that the drug is considered not effective.
In machine learning, a hypothesis is a proposed explanation or solution for a problem. It is a tentative assumption or idea that can be tested and validated using data. In supervised learning, the hypothesis is the model that the algorithm is trained on to make predictions on unseen data. The hypothesis is generally expressed as a function that ...
The null hypothesis represented as H₀ is the initial claim that is based on the prevailing belief about the population. The alternate hypothesis represented as H₁ is the challenge to the null hypothesis. It is the claim which we would like to prove as True. One of the main points which we should consider while formulating the null and alternative hypothesis is that the null hypothesis ...
The concept of a hypothesis is fundamental in Machine Learning and data science endeavours. In the realm of machine learning, a hypothesis serves as an initial assumption made by data scientists and ML professionals when attempting to address a problem. Machine learning involves conducting experiments based on past experiences, and these hypotheses
The hypothesis is a crucial aspect of Machine Learning and Data Science. It is present in all the domains of analytics and is the deciding factor of whether a change should be introduced or not. Be it pharma, software, sales, etc. A Hypothesis covers the complete training dataset to check the performance of the models from the Hypothesis space.
In this post, you will discover a cheat sheet for the most popular statistical hypothesis tests for a machine learning project with examples using the Python API. Each statistical test is presented in a consistent way, including: The name of the test. What the test is checking. The key assumptions of the test. How the test result is interpreted.
A concept class C is a set of true functions f.Hypothesis class H is the set of candidates to formulate as the final output of a learning algorithm to well approximate the true function f.Hypothesis class H is chosen before seeing the data (training process).C and H can be either same or not and we can treat them independently.
The hypothesis space is $2^ {2^4}=65536$ because for each set of features of the input space two outcomes ( 0 and 1) are possible. The ML algorithm helps us to find one function, sometimes also referred as hypothesis, from the relatively large hypothesis space. References. A Few Useful Things to Know About ML. Share.
If you manage to search over all piecewise-$\tanh^2$ functions, then those functions are what your hypothesis class includes. The big tradeoff is that the larger your hypothesis class, the better the best hypothesis models the underlying true function, but the harder it is to find that best hypothesis. This is related to the bias-variance ...
If one choose a 2nd degree hypothesis function, using your training set you can get the optimum 2nd degree hypothesis function (by training). If one choose a 3rd degree hypothesis function, by training you can get the optimum 3rd degree hypothesis function. But the optimum 2nd degree hypothesis function might be better/worse than the optimum ...
Hypothesis is a testable statement that explains what is happening or observed. It proposes the relation between the various participating variables. Hypothesis is also called Theory, Thesis, Guess, Assumption, or Suggestion. Hypothesis creates a structure that guides the search for knowledge. In this article, we will learn what is hypothesis ...
Leveraging the synergy between causal knowledge graphs and a large language model (LLM), our study introduces a groundbreaking approach for computational hypothesis generation in psychology. We ...
However, over the last two or three years, we are increasingly looking to computational approaches to predict protein interactions. There was a big breakthrough when Google DeepMind released AlphaFold, a machine-learning model that can predict protein folding. Importantly, how proteins fold determines their function and interactions.
The aim of transfer learning is to improve the performance of learning models in the target domain by transferring knowledge from the related source domain. However, not all data instances in the source domain are reliable for the learning task in the target domain. Unreliable source-domain data may lead to negative transfer.