Reset password New user? Sign up
Existing user? Log in

Hungarian Maximum Matching Algorithm
Already have an account? Log in here.
The Hungarian matching algorithm , also called the Kuhn-Munkres algorithm, is a \(O\big(|V|^3\big)\) algorithm that can be used to find maximum-weight matchings in bipartite graphs , which is sometimes called the assignment problem . A bipartite graph can easily be represented by an adjacency matrix , where the weights of edges are the entries. Thinking about the graph in terms of an adjacency matrix is useful for the Hungarian algorithm.
A matching corresponds to a choice of 1s in the adjacency matrix, with at most one 1 in each row and in each column.
The Hungarian algorithm solves the following problem:
In a complete bipartite graph \(G\), find the maximum-weight matching. (Recall that a maximum-weight matching is also a perfect matching.)
This can also be adapted to find the minimum-weight matching.
Say you are having a party and you want a musician to perform, a chef to prepare food, and a cleaning service to help clean up after the party. There are three companies that provide each of these three services, but one company can only provide one service at a time (i.e. Company B cannot provide both the cleaners and the chef). You are deciding which company you should purchase each service from in order to minimize the cost of the party. You realize that is an example of the assignment problem, and set out to make a graph out of the following information: \(\quad\) Company\(\quad\) \(\quad\) Cost for Musician\(\quad\) \(\quad\) Cost for Chef\(\quad\) \(\quad\) Cost for Cleaners\(\quad\) \(\quad\) Company A\(\quad\) \(\quad\) $108\(\quad\) \(\quad\) $125\(\quad\) \(\quad\) $150\(\quad\) \(\quad\) Company B\(\quad\) \(\quad\) $150\(\quad\) \(\quad\) $135\(\quad\) \(\quad\) $175\(\quad\) \(\quad\) Company C\(\quad\) \(\quad\) $122\(\quad\) \(\quad\) $148\(\quad\) \(\quad\) $250\(\quad\) Can you model this table as a graph? What are the nodes? What are the edges? Show Answer The nodes are the companies and the services. The edges are weighted by the price.
What are some ways to solve the problem above? Since the table above can be thought of as a \(3 \times 3\) matrix, one could certainly solve this problem using brute force, checking every combination and seeing what yields the lowest price. However, there are \(n!\) combinations to check, and for large \(n\), this method becomes very inefficient very quickly.
The Hungarian Algorithm Using an Adjacency Matrix
The hungarian algorithm using a graph.
With the cost matrix from the example above in mind, the Hungarian algorithm operates on this key idea: if a number is added to or subtracted from all of the entries of any one row or column of a cost matrix, then an optimal assignment for the resulting cost matrix is also an optimal assignment for the original cost matrix.
The Hungarian Method [1] Subtract the smallest entry in each row from all the other entries in the row. This will make the smallest entry in the row now equal to 0. Subtract the smallest entry in each column from all the other entries in the column. This will make the smallest entry in the column now equal to 0. Draw lines through the row and columns that have the 0 entries such that the fewest lines possible are drawn. If there are \(n\) lines drawn, an optimal assignment of zeros is possible and the algorithm is finished. If the number of lines is less than \(n\), then the optimal number of zeroes is not yet reached. Go to the next step. Find the smallest entry not covered by any line. Subtract this entry from each row that isn’t crossed out, and then add it to each column that is crossed out. Then, go back to Step 3.
Solve for the optimal solution for the example in the introduction using the Hungarian algorithm described above. Here is the initial adjacency matrix: Subtract the smallest value in each row from the other values in the row: Now, subtract the smallest value in each column from all other values in the column: Draw lines through the row and columns that have the 0 entries such that the fewest possible lines are drawn: There are 2 lines drawn, and 2 is less than 3, so there is not yet the optimal number of zeroes. Find the smallest entry not covered by any line. Subtract this entry from each row that isn’t crossed out, and then add it to each column that is crossed out. Then, go back to Step 3. 2 is the smallest entry. First, subtract from the uncovered rows: Now add to the covered columns: Now go back to step 3, drawing lines through the rows and columns that have 0 entries: There are 3 lines (which is \(n\)), so we are done. The assignment will be where the 0's are in the matrix such that only one 0 per row and column is part of the assignment. Replace the original values: The Hungarian algorithm tells us that it is cheapest to go with the musician from company C, the chef from company B, and the cleaners from company A. We can verify this by brute force. 108 + 135 + 250 = 493 108 + 148 + 175 = 431 150 + 125 + 250 = 525 150 + 148 + 150 = 448 122 + 125 + 175 = 422 122 + 135 + 150 = 407. We can see that 407 is the lowest price and matches the assignment the Hungarian algorithm determined. \(_\square\)
The Hungarian algorithm can also be executed by manipulating the weights of the bipartite graph in order to find a stable, maximum (or minimum) weight matching. This can be done by finding a feasible labeling of a graph that is perfectly matched, where a perfect matching is denoted as every vertex having exactly one edge of the matching.
How do we know that this creates a maximum-weight matching?
A feasible labeling on a perfect match returns a maximum-weighted matching. Suppose each edge \(e\) in the graph \(G\) connects two vertices, and every vertex \(v\) is covered exactly once. With this, we have the following inequality: \[w(M’) = \sum_{e\ \epsilon\ E} w(e) \leq \sum_{e\ \epsilon\ E } \big(l(e_x) + l(e_y)\big) = \sum_{v\ \epsilon\ V} l(v),\] where \(M’\) is any perfect matching in \(G\) created by a random assignment of vertices, and \(l(x)\) is a numeric label to node \(x\). This means that \(\sum_{v\ \epsilon\ V}\ l(v)\) is an upper bound on the cost of any perfect matching. Now let \(M\) be a perfect match in \(G\), then \[w(M) = \sum_{e\ \epsilon\ E} w(e) = \sum_{v\ \epsilon\ V}\ l(v).\] So \(w(M’) \leq w(M)\) and \(M\) is optimal. \(_\square\)
Start the algorithm by assigning any weight to each individual node in order to form a feasible labeling of the graph \(G\). This labeling will be improved upon by finding augmenting paths for the assignment until the optimal one is found.
A feasible labeling is a labeling such that
\(l(x) + l(y) \geq w(x,y)\ \forall x \in X, y \in Y\), where \(X\) is the set of nodes on one side of the bipartite graph, \(Y\) is the other set of nodes, \(l(x)\) is the label of \(x\), etc., and \(w(x,y)\) is the weight of the edge between \(x\) and \(y\).
A simple feasible labeling is just to label a node with the number of the largest weight from an edge going into the node. This is certain to be a feasible labeling because if \(A\) is a node connected to \(B\), the label of \(A\) plus the label of \(B\) is greater than or equal to the weight \(w(x,y)\) for all \(y\) and \(x\).
A feasible labeling of nodes, where labels are in red [2] .
Imagine there are four soccer players and each can play a few positions in the field. The team manager has quantified their skill level playing each position to make assignments easier.
How can players be assigned to positions in order to maximize the amount of skill points they provide?
The algorithm starts by labeling all nodes on one side of the graph with the maximum weight. This can be done by finding the maximum-weighted edge and labeling the adjacent node with it. Additionally, match the graph with those edges. If a node has two maximum edges, don’t connect them.
Although Eva is the best suited to play defense, she can't play defense and mid at the same time!
If the matching is perfect, the algorithm is done as there is a perfect matching of maximum weights. Otherwise, there will be two nodes that are not connected to any other node, like Tom and Defense. If this is the case, begin iterating.
Improve the labeling by finding the non-zero label vertex without a match, and try to find the best assignment for it. Formally, the Hungarian matching algorithm can be executed as defined below:
The Hungarian Algorithm for Graphs [3] Given: the labeling \(l\), an equality graph \(G_l = (V, E_l)\), an initial matching \(M\) in \(G_l\), and an unmatched vertex \(u \in V\) and \(u \notin M\) Augmenting the matching A path is augmenting for \(M\) in \(G_l\) if it alternates between edges in the matching and edges not in the matching, and the first and last vertices are free vertices , or unmatched, in \(M\). We will keep track of a candidate augmenting path starting at the vertex \(u\). If the algorithm finds an unmatched vertex \(v\), add on to the existing augmenting path \(p\) by adding the \(u\) to \(v\) segment. Flip the matching by replacing the edges in \(M\) with the edges in the augmenting path that are not in \(M\) \((\)in other words, the edges in \(E_l - M).\) Improving the labeling \(S \subseteq X\) and \(T \subseteq Y,\) where \(S\) and \(T\) represent the candidate augmenting alternating path between the matching and the edges not in the matching. Let \(N_l(S)\) be the neighbors to each node that is in \(S\) along edges in \(E_l\) such that \(N_l(S) = \{v|\forall u \in S: (u,v) \in E_l\}\). If \(N_l(S) = T\), then we cannot increase the size of the alternating path (and therefore can't further augment), so we need to improve the labeling. Let \(\delta_l\) be the minimum of \(l(u) + l(v) - w(u,v)\) over all of the \(u \in S\) and \(v \notin T\). Improve the labeling \(l\) to \(l'\): If \(r \in S,\) then \(l'(r) = l(r) - \delta_l,\) If \(r \in T,\) then \(l'(r) = l(r) + \delta_l.\) If \(r \notin S\) and \(r \notin T,\) then \(l'(r) = l(r).\) \(l'\) is a valid labeling and \(E_l \subset E_{l'}.\) Putting it all together: The Hungarian Algorithm Start with some matching \(M\), a valid labeling \(l\), where \(l\) is defined as the labelling \(\forall x \in X, y \in Y| l(y) = 0, l(x) = \text{ max}_{y \in Y}(w\big(x, y)\big)\). Do these steps until a perfect matching is found \((\)when \(M\) is perfect\():\) (a) Look for an augmenting path in \(M.\) (b) If an augmenting path does not exist, improve the labeling and then go back to step (a).
Each step will increase the size of the matching \(M\) or it will increase the size of the set of labeled edges, \(E_l\). This means that the process will eventually terminate since there are only so many edges in the graph \(G\). [4]
When the process terminates, \(M\) will be a perfect matching. By the Kuhn-Munkres theorem , this means that the matching is a maximum-weight matching.
The algorithm defined above can be implemented in the soccer scenario. First, the conflicting node is identified, implying that there is an alternating tree that must be reconfigured.
There is an alternating path between defense, Eva, mid, and Tom.
To find the best appropriate node, find the minimum \(\delta_l\), as defined in step 4 above, where \(l_u\) is the label for player \(u,\) \(l_v\) is the label for position \(v,\) and \(w_{u, v}\) is the weight on that edge.
The \(\delta_l\) of each unmatched node is computed, where the minimum is found to be a value of 2, between Tom playing mid \((8 + 0 – 6 = 2).\)
The labels are then augmented and the new edges are graphed in the example. Notice that defense and mid went down by 2 points, whereas Eva’s skillset got back two points. However, this is expected as Eva can't play in both positions at once.
Augmenting path leads to relabeling of nodes, which gives rise to the maximum-weighted path.
These new edges complete the perfect matching of the graph, which implies that a maximum-weighted graph has been found and the algorithm can terminate.
The complexity of the algorithm will be analyzed using the graph-based technique as a reference, yet the result is the same as for the matrix-based one.
Algorithm analysis [3] At each \(a\) or \(b\) step, the algorithm adds one edge to the matching and this happens \(O\big(|V|\big)\) times. It takes \(O\big(|V|\big)\) time to find the right vertex for the augmenting (if there is one at all), and it is \(O\big(|V|\big)\) time to flip the matching. Improving the labeling takes \(O\big(|V|\big)\) time to find \(\delta_l\) and to update the labelling accordingly. We might have to improve the labeling up to \(O\big(|V|\big)\) times if there is no augmenting path. This makes for a total of \(O\big(|V|^2\big)\) time. In all, there are \(O\big(|V|\big)\) iterations each taking \(O\big(|V|\big)\) work, leading to a total running time of \(O\big(|V|^3\big)\).
- Matching Algorithms
- Bruff, D. The Assignment Problem and the Hungarian Method . Retrieved June 26, 2016, from http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf
- Golin, M. Bipartite Matching & the Hungarian Method . Retrieved Retrieved June 26th, 2016, from http://www.cse.ust.hk/~golin/COMP572/Notes/Matching.pdf
- Grinman, A. The Hungarian Algorithm for Weighted Bipartite Graphs . Retrieved June 26, 2016, from http://math.mit.edu/~rpeng/18434/hungarianAlgorithm.pdf
- Golin, M. Bipartite Matching & the Hungarian Method . Retrieved June 26, 2016, from http://www.cse.ust.hk/~golin/COMP572/Notes/Matching.pdf
Problem Loading...
Note Loading...
Set Loading...
- DSA Tutorial
- Data Structures
- Linked List
- Dynamic Programming
- Binary Tree
- Binary Search Tree
- Divide & Conquer
- Mathematical
- Backtracking
- Branch and Bound
- Pattern Searching
Hungarian Algorithm for Assignment Problem | Set 2 (Implementation)
Given a 2D array , arr of size N*N where arr[i][j] denotes the cost to complete the j th job by the i th worker. Any worker can be assigned to perform any job. The task is to assign the jobs such that exactly one worker can perform exactly one job in such a way that the total cost of the assignment is minimized.
Input: arr[][] = {{3, 5}, {10, 1}} Output: 4 Explanation: The optimal assignment is to assign job 1 to the 1st worker, job 2 to the 2nd worker. Hence, the optimal cost is 3 + 1 = 4. Input: arr[][] = {{2500, 4000, 3500}, {4000, 6000, 3500}, {2000, 4000, 2500}} Output: 4 Explanation: The optimal assignment is to assign job 2 to the 1st worker, job 3 to the 2nd worker and job 1 to the 3rd worker. Hence, the optimal cost is 4000 + 3500 + 2000 = 9500.
Different approaches to solve this problem are discussed in this article .
Approach: The idea is to use the Hungarian Algorithm to solve this problem. The algorithm is as follows:
- For each row of the matrix, find the smallest element and subtract it from every element in its row.
- Repeat the step 1 for all columns.
- Cover all zeros in the matrix using the minimum number of horizontal and vertical lines.
- Test for Optimality : If the minimum number of covering lines is N , an optimal assignment is possible. Else if lines are lesser than N , an optimal assignment is not found and must proceed to step 5.
- Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.
Consider an example to understand the approach:
Let the 2D array be: 2500 4000 3500 4000 6000 3500 2000 4000 2500 Step 1: Subtract minimum of every row. 2500, 3500 and 2000 are subtracted from rows 1, 2 and 3 respectively. 0 1500 1000 500 2500 0 0 2000 500 Step 2: Subtract minimum of every column. 0, 1500 and 0 are subtracted from columns 1, 2 and 3 respectively. 0 0 1000 500 1000 0 0 500 500 Step 3: Cover all zeroes with minimum number of horizontal and vertical lines. Step 4: Since we need 3 lines to cover all zeroes, the optimal assignment is found. 2500 4000 3500 4000 6000 3500 2000 4000 2500 So the optimal cost is 4000 + 3500 + 2000 = 9500
For implementing the above algorithm, the idea is to use the max_cost_assignment() function defined in the dlib library . This function is an implementation of the Hungarian algorithm (also known as the Kuhn-Munkres algorithm) which runs in O(N 3 ) time. It solves the optimal assignment problem.
Below is the implementation of the above approach:
Time Complexity: O(N 3 ) Auxiliary Space: O(N 2 )
Please Login to comment...
Similar reads.
- How to Get a Free SSL Certificate
- Best SSL Certificates Provider in India
- Elon Musk's xAI releases Grok-2 AI assistant
- What is OpenAI SearchGPT? How it works and How to Get it?
- Content Improvement League 2024: From Good To A Great Article
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
Index Assignment problem Hungarian algorithm Solve online
Solve an assignment problem online
Fill in the cost matrix of an assignment problem and click on 'Solve'. The optimal assignment will be determined and a step by step explanation of the hungarian algorithm will be given.
Fill in the cost matrix ( random cost matrix ):
Don't show the steps of the Hungarian algorithm Maximize the total cost
HungarianAlgorithm.com © 2013-2024
Information
- Author Services
Initiatives
You are accessing a machine-readable page. In order to be human-readable, please install an RSS reader.
All articles published by MDPI are made immediately available worldwide under an open access license. No special permission is required to reuse all or part of the article published by MDPI, including figures and tables. For articles published under an open access Creative Common CC BY license, any part of the article may be reused without permission provided that the original article is clearly cited. For more information, please refer to https://www.mdpi.com/openaccess .
Feature papers represent the most advanced research with significant potential for high impact in the field. A Feature Paper should be a substantial original Article that involves several techniques or approaches, provides an outlook for future research directions and describes possible research applications.
Feature papers are submitted upon individual invitation or recommendation by the scientific editors and must receive positive feedback from the reviewers.
Editor’s Choice articles are based on recommendations by the scientific editors of MDPI journals from around the world. Editors select a small number of articles recently published in the journal that they believe will be particularly interesting to readers, or important in the respective research area. The aim is to provide a snapshot of some of the most exciting work published in the various research areas of the journal.
Original Submission Date Received: .
- Active Journals
- Find a Journal
- Proceedings Series
- For Authors
- For Reviewers
- For Editors
- For Librarians
- For Publishers
- For Societies
- For Conference Organizers
- Open Access Policy
- Institutional Open Access Program
- Special Issues Guidelines
- Editorial Process
- Research and Publication Ethics
- Article Processing Charges
- Testimonials
- Preprints.org
- SciProfiles
- Encyclopedia

Article Menu

- Subscribe SciFeed
- Recommended Articles
- Google Scholar
- on Google Scholar
- Table of Contents
Find support for a specific problem in the support section of our website.
Please let us know what you think of our products and services.
Visit our dedicated information section to learn more about MDPI.
JSmol Viewer
The assignment problem and its relation to logistics problems.

1. Introduction
2. the assignment problem model, 3. routing problems, 3.1. travelling salesman problem, 3.2. vehicle routing problem, 4. distribution problems, 4.1. container transportation problem, 4.2. allocation problem, 4.3. location problem, 4.4. capacitated network area coverage, 4.5. transportation problem with supply from primary source, 4.6. crop problem, 5. scheduling problems, mathematical model of pfssp.
- The first task in a permutation can always continue the next operation on the next machine without delay because it does not wait for the completion of any other operation.
- It follows from the previous conclusion that waiting times to start the operation of the first task in the permutation on the second and subsequent machines are given by the sum of the durations of the operations of that task on the previous machines.
- Equalities of 3 addition terms in Figure 1 can be generalized into a Gantt chart between all pairs of neighboring machines.
- The duration of the entire schedule (makespan) is given by the sum of the waiting times for the start of operations on the last machine and the duration of these operations.
6. Computational Results
6.1. pfssp computational results, 6.2. tsp implementation in gams, 6.3. data, changes in time, uncertainty, 7. conclusions, data availability statement, conflicts of interest, abbreviations.
| AP | Assignment Problem |
| TSP | Travelling Salesman Problem |
| VRP | Vehicle Routing Problem |
| PFSSP | Permutation Flow Shop Scheduling Problem |
| GAMS | General Algebraic Modelling System |
| GA | Genetic Algorithm |
| ANN | Artificial Neural Network |
- Gass, S.I. Linear Programming. Methods and Applications ; Dover Books on Computer Science; Courier Corporation: North Chelmsford, MA, USA, 2010. [ Google Scholar ]
- Du, D.Z.; Pardalos, P.M. Handbook of Combinatorial Optimization. Volume A ; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999. [ Google Scholar ]
- Du, D.Z.; Pardalos, P.M. Handbook of Combinatorial Optimization. Volume B ; Springer: Berlin/Heidelberg, Germany, 2005. [ Google Scholar ]
- Kuhn, H.W. The Hungarian Method for the Assignment Problem. Nav. Res. Logist. 1955 , 2 , 83–97. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Burkard, R.; Dell’Amico, M.; Martello, S. Assignment Problems ; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2009. [ Google Scholar ]
- Diestel, R. Graph Theory ; Springer: Berlin/Heidelberg, Germany, 2005. [ Google Scholar ]
- Burkard, R.E.; Cela, E.; Pardalos, P.M.; Pitsoulis, L.S. The Quadratic Assignment Problem ; Report; Graz University of Technology: Graz, Austria, 1998; p. 71. [ Google Scholar ]
- Gutin, G.; Punnen, A.P. The Traveling Salesman Problem and Its Variations ; Springer: Berlin/Heidelberg, Germany, 2007. [ Google Scholar ]
- Nalepa, J. Smart Delivery Systems. Solving Complex Vehicle Routing Problems ; Elsevier: Amsterdam, The Netherlands, 2020. [ Google Scholar ]
- Ganesh, K.; Malaijaran, R.A.; Mohapatra, S.; Punniyamoorthy, M. Resource Allocation Problems in Supply Chains ; Emerald Group Publishing Limited: Bingley, UK, 2015. [ Google Scholar ]
- Bohle, C.; Maturana, S.; Vera, J. A Robust Optimization Approach to Wine Grape Harvesting Scheduling. Eur. J. Oper. Res. 2010 , 200 , 245–252. [ Google Scholar ] [ CrossRef ]
- Church, R.L.; Murray, A. Location Covering Models ; Springer: Berlin/Heidelberg, Germany, 2018. [ Google Scholar ]
- Seda, P.; Seda, M.; Hosek, J. On Mathematical Modelling of Automated Coverage Optimization in Wireless 5G and beyond Deployments. Appl. Sci. 2020 , 10 , 8853. [ Google Scholar ] [ CrossRef ]
- Błażewicz, J.; Ecker, K.H.; Schmidt, G.; Wȩglarz, J. Scheduling Computer and Manufacturing Processes ; Springer: Berlin/Heidelberg, Germany, 2013. [ Google Scholar ]
- Rossit, D.; Vásquez, Ó.C.; Tohmé, F.; Frutos, M.; Safe, M. A Combinatorial Analysis of the Permutation and Non-Permutation Flow Shop Scheduling Problems. Eur. J. Oper. Res. 2021 , 289 , 841–854. [ Google Scholar ] [ CrossRef ]
- Ali, I.; Essam, D.; Kasmarik, K. A Novel Design of Differential Evolution for Solving Discrete Traveling Salesman Problems. Swarm Evol. Comput. 2020 , 52 , 100607. [ Google Scholar ] [ CrossRef ]
- Dong, X.; Cai, Y. A Novel Genetic Algorithm for Large Scale Colored Balanced Traveling Salesman Problem. Future Gener. Comput. Syst. 2019 , 95 , 727–742. [ Google Scholar ] [ CrossRef ]
- Placido, A.D.; Archetti, C.; Cerrone, C. A Genetic Algorithm for the Close-Enough Traveling Salesman Problem with Application to Solar Panels Diagnostic Reconnaissance. Comput. Oper. Res. 2022 , 145 , 105831. [ Google Scholar ] [ CrossRef ]
- Zhang, P.; Wang, J.; Tian, Z.; Sun, S.; Li, J.; Yang, J. A Genetic Algorithm with Jumping Gene and Heuristic Operators for Traveling Salesman Problem. Appl. Soft Comput. 2022 , 127 , 109339. [ Google Scholar ] [ CrossRef ]
- Mahrach, M.; Miranda, G.; León, C.; Segredo, E. Comparison between Single and Multi-Objective Evolutionary Algorithms to Solve the Knapsack Problem and the Travelling Salesman Problem. Mathematics 2020 , 8 , 2018. [ Google Scholar ] [ CrossRef ]
- Zhu, Y.; Chen, Y.; Fu, Z.H. Knowledge-Guided Two-Stage Memetic Search for the Pickup and Delivery Traveling Salesman Problem with FIFO Loading. Knowl.-Based Syst. 2022 , 242 , 108332. [ Google Scholar ] [ CrossRef ]
- Larasati, M.R.; Wang, I.L. An Integrated Integer Programming Model with a Simulated Annealing Heuristic for the Carrier Vehicle Traveling Salesman Problem. Procedia Comput. Sci. 2022 , 197 , 301–308. [ Google Scholar ] [ CrossRef ]
- Shi, Y.; Zhang, Y. The Neural Network Methods for Solving Traveling Salesman Problem. Procedia Comput. Sci. 2022 , 199 , 681–686. [ Google Scholar ] [ CrossRef ]
- Karakostas, P.; Sifaleras, A. A Double-Adaptive General Variable Neighborhood Search Algorithm for the Solution of the Traveling Salesman Problem. Appl. Soft Comput. 2022 , 121 , 108746. [ Google Scholar ] [ CrossRef ]
- Schmidt, J.; Irnich, S. New Neighborhoods and an Iterated Local Search Algorithm for the Generalized Traveling Salesman Problem. EURO J. Comput. Optim. 2022 , 10 , 100029. [ Google Scholar ] [ CrossRef ]
- Kanna, S.; Sivakumar, K.; Lingaraj, N. Development of Deer Hunting Linked Earthworm Optimization Algorithm for Solving Large Scale Traveling Salesman Problem. Knowl.-Based Syst. 2021 , 227 , 107199. [ Google Scholar ] [ CrossRef ]
- Akhand, M.; Ayon, S.; Shahriyar, S.; Siddique, N.; Adel, H. Discrete Spider Monkey Optimization for Travelling Salesman Problem. Appl. Soft Comput. 2020 , 86 , 105887. [ Google Scholar ] [ CrossRef ]
- Krishna, M.; Panda, N.; Majhi, S. Solving Traveling Salesman Problem Using Hybridization of Rider Optimization and Spotted Hyena Optimization Algorithm. Expert Syst. Appl. 2021 , 183 , 115353. [ Google Scholar ] [ CrossRef ]
- Panwar, K.; Deep, K. Discrete Grey Wolf Optimizer for Symmetric Travelling Salesman Problem. Appl. Soft Comput. 2021 , 105 , 107298. [ Google Scholar ] [ CrossRef ]
- Reda, M.; Onsy, A.; Elhosseini, M.A.; Haikal, A.Y.; Badawy, M. A Discrete Variant of Cuckoo Search Algorithm to Solve the Travelling Salesman Problem and Path Planning for Autonomous Trolley inside Warehouse. Knowl.-Based Syst. 2022 , 252 , 109290. [ Google Scholar ] [ CrossRef ]
- Zhang, Z.; Yang, J. A Discrete Cuckoo Search Algorithm for Traveling Salesman Problem and Its Application in Cutting Path Optimization. Comput. Ind. Eng. 2022 , 169 , 108157. [ Google Scholar ] [ CrossRef ]
- Zhang, Z.; Han, Y. Discrete Sparrow Search Algorithm for Symmetric Traveling Salesman Problem. Appl. Soft Comput. 2022 , 118 , 108469. [ Google Scholar ] [ CrossRef ]
- Huang, Y.; Shen, X.N.; You, X. A Discrete Shuffled Frog-Leaping Algorithm Based on Heuristic Information for Traveling Salesman Problem. Appl. Soft Comput. 2021 , 102 , 107085. [ Google Scholar ] [ CrossRef ]
- Stodola, P.; Otřísal, P.; Hasilová, K. Adaptive Ant Colony Optimization with Node Clustering Applied to the Travelling Salesman Problem. Swarm Evol. Comput. 2022 , 70 , 101056. [ Google Scholar ] [ CrossRef ]
- Land, A. The Solution of Some 100-City Travelling Salesman Problems. EURO J. Comput. Optim. 2021 , 9 , 100017. [ Google Scholar ] [ CrossRef ]
- Dell’Amico, M.; Montemanni, R.; Novellani, S. Algorithms Based on Branch and Bound for the Flying Sidekick Traveling Salesman Problem. Omega 2021 , 104 , 102493. [ Google Scholar ] [ CrossRef ]
- Pereira, A.; Mateus, G.; Urrutia, S. Valid Inequalities and Branch-and-Cut Algorithm for the Pickup and Delivery Traveling Salesman Problem with Multiple Stacks. Eur. J. Oper. Res. 2022 , 300 , 207–220. [ Google Scholar ] [ CrossRef ]
- Yuan, Y.; Cattaruzza, D.; Ogier, M.; Semet, F. A Branch-and-Cut Algorithm for the Generalized Traveling Salesman Problem with Time Windows. Eur. J. Oper. Res. 2020 , 286 , 849–866. [ Google Scholar ] [ CrossRef ]
- Morais, M.; Ribeiro, M.; da Silva, R.; Mariani, V.; Coelho, L. Discrete Differential Evolution Metaheuristics for Permutation Flow Shop Scheduling Problems. Comput. Ind. Eng. 2022 , 166 , 107956. [ Google Scholar ] [ CrossRef ]
- Qiao, Y.; Wu, N.; He, Y.; Li, Z.; Chen, T. Adaptive Genetic Algorithm for Two-Stage Hybrid Flow-Shop Scheduling with Sequence-Independent Setup Time and No-Interruption Requirement. Expert Syst. Appl. 2022 , 208 , 118068. [ Google Scholar ] [ CrossRef ]
- Wu, X.; Cao, Z. An Improved Multi-Objective Evolutionary Algorithm Based on Decomposition for Solving Re-Entrant Hybrid Flow Shop Scheduling Problem with Batch Processing Machines. Comput. Ind. Eng. 2022 , 169 , 108236. [ Google Scholar ] [ CrossRef ]
- Song, H.B.; Lin, J. A Genetic Programming Hyper-Heuristic for the Distributed Assembly Permutation Flow-Shop Scheduling Problem with Sequence Dependent Setup Times. Swarm Evol. Comput. 2021 , 60 , 100807. [ Google Scholar ] [ CrossRef ]
- Wang, J.J.; Wang, L. A Cooperative Memetic Algorithm with Feedback for the Energy-Aware Distributed Flow-Shops with Flexible Assembly Scheduling. Comput. Ind. Eng. 2022 , 168 , 108126. [ Google Scholar ] [ CrossRef ]
- Harbaoui, H.; Khalfallah, S. Tabu-Search Optimization Approach for No-Wait Hybrid Flow-Shop Scheduling with Dedicated Machines. Procedia Comput. Sci. 2020 , 176 , 706–712. [ Google Scholar ] [ CrossRef ]
- Doush, I.; Al-Betar, M.; Awadallah, M.; Alyasseri, Z.; Makhadmeh, S.; El-Abd, M. Island Neighboring Heuristics Harmony Search Algorithm for Flow Shop Scheduling with Blocking. Swarm Evol. Comput. 2022 , 74 , 101127. [ Google Scholar ] [ CrossRef ]
- Brum, A.; Ruiz, R.; Ritt, M. Automatic Generation of Iterated Greedy Algorithms for the Non-Permutation Flow Shop Scheduling Problem with Total Completion Time Minimization. Comput. Ind. Eng. 2022 , 163 , 107843. [ Google Scholar ] [ CrossRef ]
- Miyata, H.; Nagano, M. An Iterated Greedy Algorithm for Distributed Blocking Flow Shop with Setup Times and Maintenance Operations to Minimize Makespan. Comput. Ind. Eng. 2022 , 171 , 108366. [ Google Scholar ] [ CrossRef ]
- Schulz, S.; Neufeld, J.; Buscher, U. Multi-Objective Iterated Local Search Algorithm for Comprehensive Energy-Aware Hybrid Flow Shop Scheduling. J. Clean. Prod. 2019 , 224 , 421–434. [ Google Scholar ] [ CrossRef ]
- Shao, W.; Shao, Z.; Pi, D. Multi-Local Search-Based General Variable Neighborhood Search for Distributed Flow Shop Scheduling in Heterogeneous Multi-Factories. Appl. Soft Comput. 2022 , 125 , 109138. [ Google Scholar ] [ CrossRef ]
- Pereira, M.; Nagano, M. Hybrid Metaheuristics for the Integrated and Detailed Scheduling of Production and Delivery Operations in No-Wait Flow Shop Systems. Comput. Ind. Eng. 2022 , 170 , 108255. [ Google Scholar ] [ CrossRef ]
- Umam, M.; Mustafid, M.; Suryono, S. A Hybrid Genetic Algorithm and Tabu Search for Minimizing Makespan in Flow Shop Scheduling Problem. J. King Saud Univ. Comput. Inf. Sci. 2022 , in press . [ Google Scholar ] [ CrossRef ]
- Brammer, J.; Lutz, B.; Neumann, D. Permutation Flow Shop Scheduling with Multiple Lines and Demand Plans Using Reinforcement Learning. Eur. J. Oper. Res. 2022 , 299 , 75–86. [ Google Scholar ] [ CrossRef ]
- Pang, X.; Xue, H.; Tseng, M.L.; Lim, M.; Liu, K. Hybrid Flow Shop Scheduling Problems Using Improved Fireworks Algorithm for Permutation. Appl. Sci. 2020 , 10 , 1174. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Engin, O.; Güclü, A. A New Hybrid Ant Colony Optimization Algorithm for Solving the No-Wait Flow Shop Scheduling Problems. Appl. Soft Comput. 2018 , 72 , 166–176. [ Google Scholar ] [ CrossRef ]
- Gümüsçü, A.; Kaya, S.; Tenekeci, M.; Karaçizmeli, I.; Aydilek, I. The Impact of Local Search Strategies on Chaotic Hybrid Firefly Particle Swarm Optimization Algorithm in Flow-Shop Scheduling. J. King Saud Univ. Comput. Inf. Sci. 2022 , in press . [ Google Scholar ] [ CrossRef ]
- Deng, G.; Xu, M.; Zhang, S.; Jiang, T.; Su, Q. Migrating Birds Optimization with a Diversified Mechanism for Blocking Flow Shops to Minimize Idle and Blocking Time. Appl. Soft Comput. 2022 , 114 , 107834. [ Google Scholar ] [ CrossRef ]
- Zhang, C.; Tan, J.; Peng, K.; Gao, L.; Shen, W.; Lian, K. A Discrete Whale Swarm Algorithm for Hybrid Flow-Shop Scheduling Problem with Limited Buffers. Robot. Comput.-Integr. Manuf. 2021 , 68 , 102081. [ Google Scholar ] [ CrossRef ]
- Croce, F.; Salassa, F.; T’Kindt, V. Exact Solution of the Two-Machine Flow Shop Problem with Three Operations. Comput. Oper. Res. 2022 , 138 , 105595. [ Google Scholar ] [ CrossRef ]
- Ho, M.; Hnaien, F.; Dugardin, F. Exact Method to Optimize the Total Electricity Cost in Two-Machine Permutation Flow Shop Scheduling Problem under Time-of-Use Tariff. Comput. Oper. Res. 2022 , 144 , 10578. [ Google Scholar ] [ CrossRef ]
- Oujana, S.; Yalaoui, F.; Amodeo, L. A Linear Programming Approach for Hybrid Flexible Flow Shop with Sequence-Dependent Setup Times to Minimise Total Tardiness. IFAC PapersOnLine 2021 , 54-1 , 1162–1167. [ Google Scholar ] [ CrossRef ]
- Schaller, J.; Valente, J. Branch-and-Bound Algorithms for Minimizing Total Eearliness and Tardiness in a Two-Machine Permutation Flow Shop with Unforced Idle Allowed. Comput. Oper. Res. 2019 , 109 , 1–11. [ Google Scholar ] [ CrossRef ]
- Liu, M.; Li, Y.; Huo, Q.; Li, A.; Zhu, M.; Qu, N.; Chen, L.; Xia, M. A Two-Way Parallel Slime Mold Algorithm by Flow and Distance for the Travelling Salesman Problem. Appl. Sci. 2020 , 10 , 6180. [ Google Scholar ] [ CrossRef ]
- Golden, B.; Raghavan, S.; Wasil, E. The Vehicle Routing Problem: Latest Advances and New Challenges ; Springer: Berlin/Heidelberg, Germany, 2008. [ Google Scholar ]
- Toth, P.; Vigo, D. The Vehicle Routing Problem ; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [ Google Scholar ]
- Soto-Mendoza, V.; García-Calvillo, I.; Ruiz-y Ruiz, E.; Pérez-Terrazas, J. Comparison between Single and Multi-Objective Evolutionary Algorithms to Solve the Knapsack Problem and the Travelling Salesman Problem. Algorithms 2020 , 13 , 96. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Ochelska-Mierzejewska, J.; Poniszewska-Marańda, A.; Marańda, W. Selected Genetic Algorithms for Vehicle Routing Problem Solving. Electronics 2021 , 10 , 3147. [ Google Scholar ] [ CrossRef ]
- Desrochers, M.; Laporte, G. Improvements and Extensions to the Miller-Tucker-Zemlin Subtour Elimination Constraints. Oper. Res. Lett. 1991 , 10 , 27–36. [ Google Scholar ] [ CrossRef ]
- Stroh, M.B. A Practical Guide to Transportation and Logistics ; Logistics Network: Burr Ridge, IL, USA, 2006. [ Google Scholar ]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness , 19th ed.; W.H. Freeman and Company: New York, NY, USA, 1997. [ Google Scholar ]
- Ausiello, G.; Crescenzi, P.; Gambosi, G.; Kann, V.; Marchetti-Spaccamela, A.; Protasi, M. Complexity and Approximation: Combinatorial Optimization Problems and their Approximability Properties ; Springer: Berlin/Heidelberg, Germany, 1999. [ Google Scholar ]
- Reeves, C.R. Modern Heuristic Techniques for Combinatorial Problems ; Blackwell Scientific Publications: Oxford, UK, 1993. [ Google Scholar ]
- Michalewicz, Z.; Fogel, D.B. How to Solve It: Modern Heuristics ; Springer: Berlin/Heidelberg, Germany, 2004. [ Google Scholar ]
- Onwubolu, G.; Davendra, D. Differential Evolution. A Handbook for Global Permutation-Based Combinatorial Optimization ; Springer: Berlin/Heidelberg, Germany, 2009. [ Google Scholar ]
- Wolpert, D.H.; McReady, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997 , 1 , 67–82. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Wolpert, D.H.; McReady, W.G. Coevolutionary Free Lunches. IEEE Trans. Evol. Comput. 2005 , 9 , 721–735. [ Google Scholar ] [ CrossRef ]
- Brooke, A.; Kendrick, D.; Meeraus, A. GAMS Release 2.25. A User’s Guide ; The Scientific Press. Boyd & Fraser Publishing Company: Boston, MA, USA, 1992. [ Google Scholar ]
- Rosenthal, R.E. GAMS—A User’s Guide ; GAMS Development Corporation: Washington, DC, USA, 2016. [ Google Scholar ]
- GAMS. Solver Manuals. Report, GAMS Development Corporation. Available online: https://www.gams.com/latest/docs/S_MAIN.html (accessed on 6 September 2022).
- Seda, P.; Mark, M.; Su, K.W.; Seda, M.; Hosek, J.; Leu, J. The Minimization of Public Facilities With Enhanced Genetic Algorithms Using War Elimination. IEEE Access 2019 , 7 , 9395–9405. [ Google Scholar ] [ CrossRef ]
- Beasley, J.E. OR-Library. Report, Brunel University London. 2018. Available online: http://people.brunel.ac.uk/~mastjjb/jeb/info.html (accessed on 6 September 2022).
- Beasley, J.E. OR-Library: Distributing Test Problems by Electronic Mail. J. Oper. Res. Soc. 1990 , 41 , 1069–1072. [ Google Scholar ] [ CrossRef ]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs ; Springer: Berlin/Heidelberg, Germany, 1998. [ Google Scholar ]
- Reinelt, G. MP-TESTDATA—The TSPLIB Symmetric Traveling Salesman Problem Instances ; Report; Heidelberg University: Heidelberg, Germany, 2013; Available online: http://elib.zib.de/pub/mp-testdata/tsp/tsplib/tsp (accessed on 6 September 2022).
- Alkaya, A.F.; Yildirim, S.; Aksakalli, V. Heuristics for the Canadian Traveler Problem with Neutralizations. Comput. Ind. Eng. 2019 , 159 , 107488. [ Google Scholar ] [ CrossRef ]
- Liao, C.S.; Huang, Y. The Covering Canadian Traveller Problem. Theor. Comput. Sci. 2014 , 530 , 80–88. [ Google Scholar ] [ CrossRef ]
- Aurenhammer, F. Voronoi Diagrams. A Survey of a Fundamental Geometric Data Structure. ACM Comput. Surv. 1991 , 23 , 345–405. [ Google Scholar ] [ CrossRef ]
- de Berg, M.; Cheong, O.; van Kreveld, M.; Overmars, M. Computational Geometry: Algorithms and Applications ; Springer: Berlin/Heidelberg, Germany, 2008. [ Google Scholar ]
- Becerra, P.; Mula, J.; Sanchis, R. Green Supply Chain Quantitative Models for Sustainable Inventory Management: A Review. J. Clean. Prod. 2021 , 328 , 129544. [ Google Scholar ] [ CrossRef ]
- Forkan, M.; Rizvi, M.M.; Chowdhury, M.A.M. Multiobjective Reverse Logistics Model for Inventory Management with Eenvironmental Impacts: An Application in Industry. Intell. Syst. Appl. 2022 , 14 , 200078. [ Google Scholar ]
- Teerasoponpong, S.; Sopadang, A. Decision Support System for Adaptive Sourcing and Inventory Management in Small- and Medium-Sized Enterprises. Robot. Comput.-Integr. Manuf. 2022 , 73 , 102226. [ Google Scholar ] [ CrossRef ]
- Xiong, X.; Li, Y.; Yang, W.; Shen, H. Data-Driven Robust Dual-Sourcing Inventory Management under Purchase Price and Demand Uncertainties. Transp. Res. Part E 2022 , 160 , 102671. [ Google Scholar ] [ CrossRef ]
- Sarkar, B.; Kar, S.; Basu, K.; Guchhait, R. A Sustainable Managerial Decision-Making Problem for a Substitutable Product in a Dual-Channel under Carbon Tax Policy. Comput. Ind. Eng. 2022 , 172 , 108635. [ Google Scholar ] [ CrossRef ]
- Sarkar, A.; Guchhait, R.; Sarkar, B. Application of the Artificial Neural Network with Multithreading within an Inventory Model under Uncertainty and Inflation. Int. J. Fuzzy Syst. 2022 , 24 , 2318–2332. [ Google Scholar ] [ CrossRef ]
- Guchhait, R.; Sarkar, B. Economic and Environmental Assessment of an Unreliable Supply Chain Management. RAIRO Oper. Res. 2021 , 55 , 3153–3170. [ Google Scholar ] [ CrossRef ]
- Seda, M. Steiner Tree Problem in Graphs and Mixed Integer Linear Programming-Based Approach in GAMS. WSEAS Trans. Comput. 2022 , 21 , 257–262. [ Google Scholar ] [ CrossRef ]
Click here to enlarge figure
| Benchmark | Result/Optimum/Early End | Time [S] | Iterations |
|---|---|---|---|
| 7720/7720/no | 0.75 | 31,535 | |
| 7038/7038/no | 0.13 | 243 | |
| 7312/7312/no | 0.42 | 13,095 | |
| 7166/7166/no | 0.20 | 650 | |
| 8003/8003/no | 0.13 | 262 | |
| 1566/1566/no | 164.45 | 2,619,405 | |
| 2120/2093/t-l-e | 1000.02 | 6,398,821 | |
| 2692/2513/t-l-e | 1000.02 | 4,886,367 | |
| 3190/3045/t-l-e | 1000.03 | 3,164,599 | |
| 5372/in [4890, 4951]/t-l-e | 1000.03 | 2,145,971 |
| Benchmark | Average Result/the Best Result | Optimum |
|---|---|---|
| 2126/2099 | 2093 | |
| 2570/2525 | 2513 | |
| 3132/3090 | 3045 | |
| 5261/5203 | between 4890 and 4951 |
| MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
Share and Cite
Seda, M. The Assignment Problem and Its Relation to Logistics Problems. Algorithms 2022 , 15 , 377. https://doi.org/10.3390/a15100377
Seda M. The Assignment Problem and Its Relation to Logistics Problems. Algorithms . 2022; 15(10):377. https://doi.org/10.3390/a15100377
Seda, Milos. 2022. "The Assignment Problem and Its Relation to Logistics Problems" Algorithms 15, no. 10: 377. https://doi.org/10.3390/a15100377
Article Metrics
Article access statistics, further information, mdpi initiatives, follow mdpi.

Subscribe to receive issue release notifications and newsletters from MDPI journals
Hungarian Method

The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.
Hungarian Method to Solve Assignment Problems
The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.

What is an Assignment Problem?
A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.
Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.
Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.
Hungarian Method Steps
Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.
Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.
Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.
Step 3 – Assign zeros
- Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
- Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.
Step 4 – Perform the Optimal Test
- The present assignment is optimal if each row and column has exactly one encircled zero.
- The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.
Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:
(a) Highlight the rows that aren’t assigned.
(b) Label the columns with zeros in marked rows (if they haven’t already been marked).
(c) Highlight the rows that have assignments in indicated columns (if they haven’t previously been marked).
(d) Continue with (b) and (c) until no further marking is needed.
(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.
Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.
Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.
|
|
|---|
Hungarian Method Example
Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.
\(\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
With 5 jobs and 5 men, the stated problem is balanced.
\(\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} \)
Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} \)
When the zeros are assigned, we get the following:
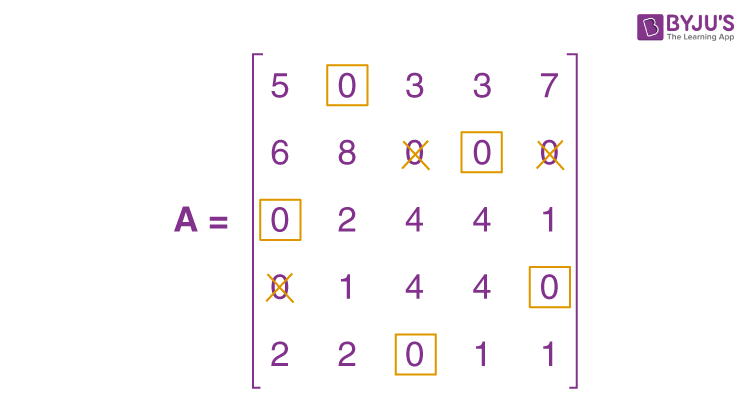
The present assignment is optimal because each row and column contain precisely one encircled zero.
Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.
Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.
Practice Question on Hungarian Method
Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.
\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)
Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.
Frequently Asked Questions on Hungarian Method
What is hungarian method.
The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.
What are the steps involved in Hungarian method?
The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.
What is the purpose of the Hungarian method?
When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
Solving assignment problem using min-cost-flow ¶
The assignment problem has two equivalent statements:
- Given a square matrix $A[1..N, 1..N]$ , you need to select $N$ elements in it so that exactly one element is selected in each row and column, and the sum of the values of these elements is the smallest.
- There are $N$ orders and $N$ machines. The cost of manufacturing on each machine is known for each order. Only one order can be performed on each machine. It is required to assign all orders to the machines so that the total cost is minimized.
Here we will consider the solution of the problem based on the algorithm for finding the minimum cost flow (min-cost-flow) , solving the assignment problem in $\mathcal{O}(N^3)$ .
Description ¶
Let's build a bipartite network: there is a source $S$ , a drain $T$ , in the first part there are $N$ vertices (corresponding to rows of the matrix, or orders), in the second there are also $N$ vertices (corresponding to the columns of the matrix, or machines). Between each vertex $i$ of the first set and each vertex $j$ of the second set, we draw an edge with bandwidth 1 and cost $A_{ij}$ . From the source $S$ we draw edges to all vertices $i$ of the first set with bandwidth 1 and cost 0. We draw an edge with bandwidth 1 and cost 0 from each vertex of the second set $j$ to the drain $T$ .
We find in the resulting network the maximum flow of the minimum cost. Obviously, the value of the flow will be $N$ . Further, for each vertex $i$ of the first segment there is exactly one vertex $j$ of the second segment, such that the flow $F_{ij}$ = 1. Finally, this is a one-to-one correspondence between the vertices of the first segment and the vertices of the second part, which is the solution to the problem (since the found flow has a minimal cost, then the sum of the costs of the selected edges will be the lowest possible, which is the optimality criterion).
The complexity of this solution of the assignment problem depends on the algorithm by which the search for the maximum flow of the minimum cost is performed. The complexity will be $\mathcal{O}(N^3)$ using Dijkstra or $\mathcal{O}(N^4)$ using Bellman-Ford . This is due to the fact that the flow is of size $O(N)$ and each iteration of Dijkstra algorithm can be performed in $O(N^2)$ , while it is $O(N^3)$ for Bellman-Ford.
Implementation ¶
The implementation given here is long, it can probably be significantly reduced. It uses the SPFA algorithm for finding shortest paths.
- Daili01 (75.89%)
- prpr (12.5%)
- Oleksandr Kulkov (7.14%)
- Shadab Zafar (2.68%)
- Jakob Kogler (0.89%)
- Hasan-Mesbaul-Ali-Taher (0.89%)
Browse Course Material
Course info, instructors.
- Prof. Erik Demaine
- Prof. Srini Devadas
- Prof. Nancy Lynch
Departments
- Electrical Engineering and Computer Science
- Mathematics
As Taught In
- Algorithms and Data Structures
- Computer Networks
- Cryptography
- Applied Mathematics
Learning Resource Types
Design and analysis of algorithms, assignments, problem sets.
Ten problem sets will be assigned during the semester.
Problem sets should be submitted in PDF format. Formatting your problem set in LaTeX will make it easier for us to read; however, any method of generating the PDF is acceptable (including scanning handwritten documents), as long as it is clearly legible.
The problem sets include exercises that should be solved but not handed in. These questions are intended to help you master the course material and will be useful in solving the assigned problems. Material covered in exercises will be tested on exams.
Guide to Writing Up Homework
You should be as clear and precise as possible in your write-up of solutions. Understandability of your answer is as desirable as correctness, because communication of technical material is an important skill.
A simple, direct analysis is worth more points than a convoluted one, both because it is simpler and less prone to error and because it is easier to read and understand. Sloppy answers will receive fewer points, even if they are correct, so make sure that your handwriting and your thoughts are legible. If writing your problem set by hand, it is a good idea to copy over your solutions to hand in, which will make your work neater and give you a chance to do sanity checks and correct bugs. If typesetting, reviewing the problem set while typing it in often has this effect. In either case, going over your solution at least once before submitting it is strongly recommended.
You will often be called upon to “give an algorithm” to solve a certain problem. Your write-up should take the form of a short essay. A topic paragraph should summarize the problem you are solving and what your results are. The body of your essay should provide the following:
- A description of the algorithm in English and, if helpful, pseudocode.
- At least one worked example or diagram to show more precisely how your algorithm works.
- A proof (or indication) of the correctness of the algorithm.
- An analysis of the running time of the algorithm.
Remember, your goal is to communicate. Graders will be instructed to take off points for convoluted and obtuse descriptions.
| ASSIGNMENTS | SOLUTIONS |
|---|---|
LaTeX Template for Problem Sets (ZIP) (This file contains: 1 .cls file, 2 .sty files, 1 .pdf file and 1 .tex file.)

You are leaving MIT OpenCourseWare

IMAGES
VIDEO
COMMENTS
In the balanced assignment problem, both parts of the bipartite graph have the same number of vertices, denoted by n. One of the first polynomial-time algorithms for balanced assignment was the Hungarian algorithm. It is a global algorithm - it is based on improving a matching along augmenting paths (alternating paths between unmatched vertices).
Hungarian algorithm steps for minimization problem. Step 1: For each row, subtract the minimum number in that row from all numbers in that row. Step 2: For each column, subtract the minimum number in that column from all numbers in that column. Step 3: Draw the minimum number of lines to cover all zeroes.
The Hungarian algorithm, aka Munkres assignment algorithm, utilizes the following theorem for polynomial runtime complexity (worst case O(n 3)) and guaranteed optimality: If a number is added to or subtracted from all of the entries of any one row or column of a cost matrix, then an optimal assignment for the resulting cost matrix is also an ...
Solution 2: Hungarian Algorithm The optimal assignment can be found using the Hungarian algorithm. The Hungarian algorithm has worst case run-time complexity of O(n^3). Solution 3: DFS/BFS on state space tree A state space tree is a N-ary tree with property that any path from root to leaf node holds one of many solutions to given problem.
The algorithm maintains a matching M and compatible prices p. Pf. Follows from Lemmas 2 and 3 and initial choice of prices. ! Theorem. The algorithm returns a min cost perfect matching. Pf. Upon termination M is a perfect matching, and p are compatible Optimality follows from Observation 2. ! Theorem. The algorithm can be implemented in O(n 3 ...
The Hungarian matching algorithm, also called the Kuhn-Munkres algorithm, is a O\big (|V|^3\big) O(∣V ∣3) algorithm that can be used to find maximum-weight matchings in bipartite graphs, which is sometimes called the assignment problem. A bipartite graph can easily be represented by an adjacency matrix, where the weights of edges are the ...
Hungarian method for assignment problem Step 1. Subtract the entries of each row by the row minimum. Step 2. Subtract the entries of each column by the column minimum. Step 3. Make an assignment to the zero entries in the resulting matrix. A = M 17 10 15 17 18 M 6 10 20 12 5 M 14 19 12 11 15 M 7 16 21 18 6 M −10
General description of the algorithm. This problem is known as the assignment problem. The assignment problem is a special case of the transportation problem, which in turn is a special case of the min-cost flow problem, so it can be solved using algorithms that solve the more general cases. Also, our problem is a special case of binary integer ...
The assignment problem is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics. In an ... The Simplex Algorithm is a general purpose algorithm to find the maximum/minimum of a linear cost function with linear constraints.
The Hungarian method is a combinatorial optimization algorithm which solves the assignment problem in polynomial time . Later it was discovered that it was a primal-dual Simplex method.. It was developed and published by Harold Kuhn in 1955, who gave the name "Hungarian method" because the algorithm was largely based on the earlier works of two Hungarian mathematicians: Denes Konig and Jeno ...
The classical solution to the assignment problem is given by the Hungarian or Kuhn-Munkres algorithm, originally proposed by H. W. Kuhn in 1955 [3] and refined by J. Munkres in 1957 [5]. The Hungarian algorithm solves the assignment problem in O(n3) time, where n is the size of one partition of the bipartite graph. This and other
advantage of it- this is the Hungarian Algorithm. The Hungarian Algorithm The Hungarian Algorithm is an algorithm designed to solve the assignment problem. We'll sum-marize it, but let's try the MachineCo problem as an example of how this algorithm will work. First, we build a table with just our costs (or in this case, our times): 1
The total time required is then 69 + 37 + 11 + 23 = 140 minutes. All other assignments lead to a larger amount of time required. The Hungarian algorithm can be used to find this optimal assignment. The steps of the Hungarian algorithm can be found here, and an explanation of the Hungarian algorithm based on the example above can be found here.
The matrix below shows the cost of assigning a certain worker to a certain job. The objective is to minimize the total cost of the assignment. Below we will explain the Hungarian algorithm using this example. Note that a general description of the algorithm can be found here. Step 1: Subtract row minima.
For implementing the above algorithm, the idea is to use the max_cost_assignment() function defined in the dlib library. This function is an implementation of the Hungarian algorithm (also known as the Kuhn-Munkres algorithm) which runs in O(N 3) time. It solves the optimal assignment problem. Below is the implementation of the above approach:
Solve an assignment problem online. Fill in the cost matrix of an assignment problem and click on 'Solve'. The optimal assignment will be determined and a step by step explanation of the hungarian algorithm will be given. Fill in the cost matrix (random cost matrix):
The assignment problem is a problem that takes many forms in optimization and graph theory, and by changing some of the constraints or interpreting them differently and adding other constraints, it can be converted to routing, distribution, and scheduling problems. Showing such correlations is one of the aims of this paper. For some of the derived problems having exponential time complexity ...
The Hungarian Method: The following algorithm applies the above theorem to a given n × n cost matrix to find an optimal assignment. Step 1. Subtract the smallest entry in each row from all the entries of its ... above) is an algorithm which finds an optimal assignment for a given cost matrix. 31. Title: assignment_overheads.dvi Created Date:
The Hungarian method is a combinatorial optimization algorithm that solves the assignment problem in polynomial time and which anticipated later primal-dual methods.It was developed and published in 1955 by Harold Kuhn, who gave it the name "Hungarian method" because the algorithm was largely based on the earlier works of two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry.
The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term "Hungarian method" to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let's go through the steps of the Hungarian method with the help of a solved example.
THE HUNGARIAN METHOD FOR THE ASSIGNMENT. PROBLEM'. H. W. Kuhn. Bryn Y a w College. Assuming that numerical scores are available for the perform- ance of each of n persons on each of n jobs, the "assignment problem" is the quest for an assignment of persons to jobs so that the sum of the. n scores so obtained is as large as possible.
The complexity of this solution of the assignment problem depends on the algorithm by which the search for the maximum flow of the minimum cost is performed. The complexity will be $\mathcal{O}(N^3)$ using Dijkstra or $\mathcal{O}(N^4)$ using Bellman-Ford.
A description of the algorithm in English and, if helpful, pseudocode. At least one worked example or diagram to show more precisely how your algorithm works. A proof (or indication) of the correctness of the algorithm. An analysis of the running time of the algorithm. Remember, your goal is to communicate.