stages of problem solving psychology example

7.3 Problem-Solving

Learning objectives.

By the end of this section, you will be able to:

• Describe problem solving strategies
• Define algorithm and heuristic
• Explain some common roadblocks to effective problem solving

   People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy for solving the problem.

The study of human and animal problem solving processes has provided much insight toward the understanding of our conscious experience and led to advancements in computer science and artificial intelligence. Essentially much of cognitive science today represents studies of how we consciously and unconsciously make decisions and solve problems. For instance, when encountered with a large amount of information, how do we go about making decisions about the most efficient way of sorting and analyzing all the information in order to find what you are looking for as in visual search paradigms in cognitive psychology. Or in a situation where a piece of machinery is not working properly, how do we go about organizing how to address the issue and understand what the cause of the problem might be. How do we sort the procedures that will be needed and focus attention on what is important in order to solve problems efficiently. Within this section we will discuss some of these issues and examine processes related to human, animal and computer problem solving.

PROBLEM-SOLVING STRATEGIES

   When people are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution.

Problems themselves can be classified into two different categories known as ill-defined and well-defined problems (Schacter, 2009). Ill-defined problems represent issues that do not have clear goals, solution paths, or expected solutions whereas well-defined problems have specific goals, clearly defined solutions, and clear expected solutions. Problem solving often incorporates pragmatics (logical reasoning) and semantics (interpretation of meanings behind the problem), and also in many cases require abstract thinking and creativity in order to find novel solutions. Within psychology, problem solving refers to a motivational drive for reading a definite “goal” from a present situation or condition that is either not moving toward that goal, is distant from it, or requires more complex logical analysis for finding a missing description of conditions or steps toward that goal. Processes relating to problem solving include problem finding also known as problem analysis, problem shaping where the organization of the problem occurs, generating alternative strategies, implementation of attempted solutions, and verification of the selected solution. Various methods of studying problem solving exist within the field of psychology including introspection, behavior analysis and behaviorism, simulation, computer modeling, and experimentation.

A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them (table below). For example, a well-known strategy is trial and error. The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.

   Another type of strategy is an algorithm. An algorithm is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?

A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):

• When one is faced with too much information
• When the time to make a decision is limited
• When the decision to be made is unimportant
• When there is access to very little information to use in making the decision
• When an appropriate heuristic happens to come to mind in the same moment

Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.

Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.

Further problem solving strategies have been identified (listed below) that incorporate flexible and creative thinking in order to reach solutions efficiently.

Additional Problem Solving Strategies :

• Abstraction – refers to solving the problem within a model of the situation before applying it to reality.
• Analogy – is using a solution that solves a similar problem.
• Brainstorming – refers to collecting an analyzing a large amount of solutions, especially within a group of people, to combine the solutions and developing them until an optimal solution is reached.
• Divide and conquer – breaking down large complex problems into smaller more manageable problems.
• Hypothesis testing – method used in experimentation where an assumption about what would happen in response to manipulating an independent variable is made, and analysis of the affects of the manipulation are made and compared to the original hypothesis.
• Lateral thinking – approaching problems indirectly and creatively by viewing the problem in a new and unusual light.
• Means-ends analysis – choosing and analyzing an action at a series of smaller steps to move closer to the goal.
• Method of focal objects – putting seemingly non-matching characteristics of different procedures together to make something new that will get you closer to the goal.
• Morphological analysis – analyzing the outputs of and interactions of many pieces that together make up a whole system.
• Proof – trying to prove that a problem cannot be solved. Where the proof fails becomes the starting point or solving the problem.
• Reduction – adapting the problem to be as similar problems where a solution exists.
• Research – using existing knowledge or solutions to similar problems to solve the problem.
• Root cause analysis – trying to identify the cause of the problem.

The strategies listed above outline a short summary of methods we use in working toward solutions and also demonstrate how the mind works when being faced with barriers preventing goals to be reached.

One example of means-end analysis can be found by using the Tower of Hanoi paradigm . This paradigm can be modeled as a word problems as demonstrated by the Missionary-Cannibal Problem :

Missionary-Cannibal Problem

Three missionaries and three cannibals are on one side of a river and need to cross to the other side. The only means of crossing is a boat, and the boat can only hold two people at a time. Your goal is to devise a set of moves that will transport all six of the people across the river, being in mind the following constraint: The number of cannibals can never exceed the number of missionaries in any location. Remember that someone will have to also row that boat back across each time.

Hint : At one point in your solution, you will have to send more people back to the original side than you just sent to the destination.

The actual Tower of Hanoi problem consists of three rods sitting vertically on a base with a number of disks of different sizes that can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top making a conical shape. The objective of the puzzle is to move the entire stack to another rod obeying the following rules:

• 1. Only one disk can be moved at a time.
• 2. Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
• 3. No disc may be placed on top of a smaller disk.

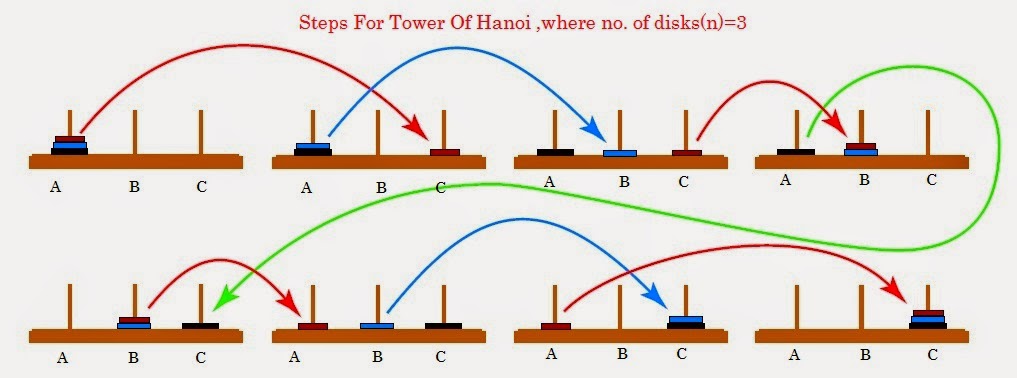
  Figure 7.02. Steps for solving the Tower of Hanoi in the minimum number of moves when there are 3 disks.

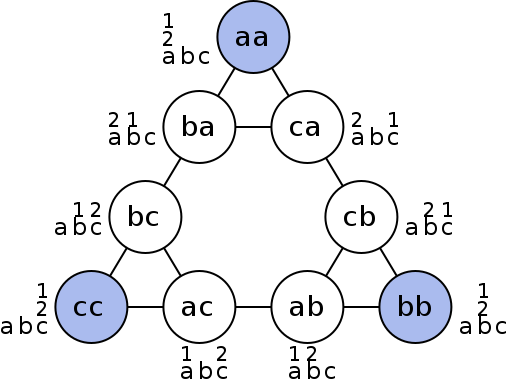
Figure 7.03. Graphical representation of nodes (circles) and moves (lines) of Tower of Hanoi.

The Tower of Hanoi is a frequently used psychological technique to study problem solving and procedure analysis. A variation of the Tower of Hanoi known as the Tower of London has been developed which has been an important tool in the neuropsychological diagnosis of executive function disorders and their treatment.

GESTALT PSYCHOLOGY AND PROBLEM SOLVING

As you may recall from the sensation and perception chapter, Gestalt psychology describes whole patterns, forms and configurations of perception and cognition such as closure, good continuation, and figure-ground. In addition to patterns of perception, Wolfgang Kohler, a German Gestalt psychologist traveled to the Spanish island of Tenerife in order to study animals behavior and problem solving in the anthropoid ape.

As an interesting side note to Kohler’s studies of chimp problem solving, Dr. Ronald Ley, professor of psychology at State University of New York provides evidence in his book A Whisper of Espionage  (1990) suggesting that while collecting data for what would later be his book  The Mentality of Apes (1925) on Tenerife in the Canary Islands between 1914 and 1920, Kohler was additionally an active spy for the German government alerting Germany to ships that were sailing around the Canary Islands. Ley suggests his investigations in England, Germany and elsewhere in Europe confirm that Kohler had served in the German military by building, maintaining and operating a concealed radio that contributed to Germany’s war effort acting as a strategic outpost in the Canary Islands that could monitor naval military activity approaching the north African coast.

While trapped on the island over the course of World War 1, Kohler applied Gestalt principles to animal perception in order to understand how they solve problems. He recognized that the apes on the islands also perceive relations between stimuli and the environment in Gestalt patterns and understand these patterns as wholes as opposed to pieces that make up a whole. Kohler based his theories of animal intelligence on the ability to understand relations between stimuli, and spent much of his time while trapped on the island investigation what he described as  insight , the sudden perception of useful or proper relations. In order to study insight in animals, Kohler would present problems to chimpanzee’s by hanging some banana’s or some kind of food so it was suspended higher than the apes could reach. Within the room, Kohler would arrange a variety of boxes, sticks or other tools the chimpanzees could use by combining in patterns or organizing in a way that would allow them to obtain the food (Kohler & Winter, 1925).

While viewing the chimpanzee’s, Kohler noticed one chimp that was more efficient at solving problems than some of the others. The chimp, named Sultan, was able to use long poles to reach through bars and organize objects in specific patterns to obtain food or other desirables that were originally out of reach. In order to study insight within these chimps, Kohler would remove objects from the room to systematically make the food more difficult to obtain. As the story goes, after removing many of the objects Sultan was used to using to obtain the food, he sat down ad sulked for a while, and then suddenly got up going over to two poles lying on the ground. Without hesitation Sultan put one pole inside the end of the other creating a longer pole that he could use to obtain the food demonstrating an ideal example of what Kohler described as insight. In another situation, Sultan discovered how to stand on a box to reach a banana that was suspended from the rafters illustrating Sultan’s perception of relations and the importance of insight in problem solving.

Grande (another chimp in the group studied by Kohler) builds a three-box structure to reach the bananas, while Sultan watches from the ground.  Insight , sometimes referred to as an “Ah-ha” experience, was the term Kohler used for the sudden perception of useful relations among objects during problem solving (Kohler, 1927; Radvansky & Ashcraft, 2013).

Solving puzzles.

   Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below (see figure) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.

How long did it take you to solve this sudoku puzzle? (You can see the answer at the end of this section.)

   Here is another popular type of puzzle (figure below) that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:

Did you figure it out? (The answer is at the end of this section.) Once you understand how to crack this puzzle, you won’t forget.

   Take a look at the “Puzzling Scales” logic puzzle below (figure below). Sam Loyd, a well-known puzzle master, created and refined countless puzzles throughout his lifetime (Cyclopedia of Puzzles, n.d.).

What steps did you take to solve this puzzle? You can read the solution at the end of this section.

Pitfalls to problem solving.

   Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Albert Einstein once said, “Insanity is doing the same thing over and over again and expecting a different result.” Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but she just needs to go to another doorway, instead of trying to get out through the locked doorway. A mental set is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now.

Functional fixedness is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. During the Apollo 13 mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.

   Researchers have investigated whether functional fixedness is affected by culture. In one experiment, individuals from the Shuar group in Ecuador were asked to use an object for a purpose other than that for which the object was originally intended. For example, the participants were told a story about a bear and a rabbit that were separated by a river and asked to select among various objects, including a spoon, a cup, erasers, and so on, to help the animals. The spoon was the only object long enough to span the imaginary river, but if the spoon was presented in a way that reflected its normal usage, it took participants longer to choose the spoon to solve the problem. (German & Barrett, 2005). The researchers wanted to know if exposure to highly specialized tools, as occurs with individuals in industrialized nations, affects their ability to transcend functional fixedness. It was determined that functional fixedness is experienced in both industrialized and nonindustrialized cultures (German & Barrett, 2005).

In order to make good decisions, we use our knowledge and our reasoning. Often, this knowledge and reasoning is sound and solid. Sometimes, however, we are swayed by biases or by others manipulating a situation. For example, let’s say you and three friends wanted to rent a house and had a combined target budget of $1,600. The realtor shows you only very run-down houses for $1,600 and then shows you a very nice house for $2,000. Might you ask each person to pay more in rent to get the $2,000 home? Why would the realtor show you the run-down houses and the nice house? The realtor may be challenging your anchoring bias. An anchoring bias occurs when you focus on one piece of information when making a decision or solving a problem. In this case, you’re so focused on the amount of money you are willing to spend that you may not recognize what kinds of houses are available at that price point.

The confirmation bias is the tendency to focus on information that confirms your existing beliefs. For example, if you think that your professor is not very nice, you notice all of the instances of rude behavior exhibited by the professor while ignoring the countless pleasant interactions he is involved in on a daily basis. Hindsight bias leads you to believe that the event you just experienced was predictable, even though it really wasn’t. In other words, you knew all along that things would turn out the way they did. Representative bias describes a faulty way of thinking, in which you unintentionally stereotype someone or something; for example, you may assume that your professors spend their free time reading books and engaging in intellectual conversation, because the idea of them spending their time playing volleyball or visiting an amusement park does not fit in with your stereotypes of professors.

Finally, the availability heuristic is a heuristic in which you make a decision based on an example, information, or recent experience that is that readily available to you, even though it may not be the best example to inform your decision . Biases tend to “preserve that which is already established—to maintain our preexisting knowledge, beliefs, attitudes, and hypotheses” (Aronson, 1995; Kahneman, 2011). These biases are summarized in the table below.

Were you able to determine how many marbles are needed to balance the scales in the figure below? You need nine. Were you able to solve the problems in the figures above? Here are the answers.

   Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. Roadblocks to problem solving include a mental set, functional fixedness, and various biases that can cloud decision making skills.

References:

Openstax Psychology text by Kathryn Dumper, William Jenkins, Arlene Lacombe, Marilyn Lovett and Marion Perlmutter licensed under CC BY v4.0. https://openstax.org/details/books/psychology

Review Questions:

1. A specific formula for solving a problem is called ________.

a. an algorithm

b. a heuristic

c. a mental set

d. trial and error

2. Solving the Tower of Hanoi problem tends to utilize a  ________ strategy of problem solving.

a. divide and conquer

b. means-end analysis

d. experiment

3. A mental shortcut in the form of a general problem-solving framework is called ________.

4. Which type of bias involves becoming fixated on a single trait of a problem?

a. anchoring bias

b. confirmation bias

c. representative bias

d. availability bias

5. Which type of bias involves relying on a false stereotype to make a decision?

6. Wolfgang Kohler analyzed behavior of chimpanzees by applying Gestalt principles to describe ________.

a. social adjustment

b. student load payment options

c. emotional learning

d. insight learning

7. ________ is a type of mental set where you cannot perceive an object being used for something other than what it was designed for.

a. functional fixedness

c. working memory

Critical Thinking Questions:

1. What is functional fixedness and how can overcoming it help you solve problems?

2. How does an algorithm save you time and energy when solving a problem?

Personal Application Question:

1. Which type of bias do you recognize in your own decision making processes? How has this bias affected how you’ve made decisions in the past and how can you use your awareness of it to improve your decisions making skills in the future?

anchoring bias

availability heuristic

confirmation bias

functional fixedness

hindsight bias

problem-solving strategy

representative bias

trial and error

working backwards

Answers to Exercises

algorithm:  problem-solving strategy characterized by a specific set of instructions

anchoring bias:  faulty heuristic in which you fixate on a single aspect of a problem to find a solution

availability heuristic:  faulty heuristic in which you make a decision based on information readily available to you

confirmation bias:  faulty heuristic in which you focus on information that confirms your beliefs

functional fixedness:  inability to see an object as useful for any other use other than the one for which it was intended

heuristic:  mental shortcut that saves time when solving a problem

hindsight bias:  belief that the event just experienced was predictable, even though it really wasn’t

mental set:  continually using an old solution to a problem without results

problem-solving strategy:  method for solving problems

representative bias:  faulty heuristic in which you stereotype someone or something without a valid basis for your judgment

trial and error:  problem-solving strategy in which multiple solutions are attempted until the correct one is found

working backwards:  heuristic in which you begin to solve a problem by focusing on the end result

Share This Book

• Increase Font Size

Psychological Steps Involved in Problem Solving

A mental process or a phenomenon dedicated towards solving problems by discovering and analyzing the problem is referred to as problem-solving. It is a process dedicated to finding not just any solution, but the best solution to resolve any problems. There is no such thing as one best way to solve every kind of problem, since there are unique problems depending upon the situation there are unique solutions too.

In psychology, problem solving doesn’t necessarily refer to solving psychological/mental issues of the brain. The process simply refers to solving every kind of problems in life in a proper manner. The idea of including the subject in psychology is because psychology deals with the overall mental process. And, tactfully using our thought process is what leads to the solution of any problems.

There are number of rigid psychological steps involved in problem solving, which is also referred as problem-solving cycle. The steps are in sequential order, and solving any problem requires following them one after another. But, we tend to avoid following this rigid set of steps, which is why it often requires us to go through the same steps over and over again until a satisfactory solution is reached.

Here are the steps involved in problem solving, approved by expert psychologists.

1. Identifying the Problem

Identifying the problem seems like the obvious first stem, but it’s not exactly as simple as it sounds. People might identify the wrong source of a problem, which will render the steps thus carried on useless.

For instance , let’s say you’re having trouble with your studies. identifying the root of your failure is your first priority. The problem here could be that you haven’t been allocating enough time for your studies, or you haven’t tried the right techniques. But, if you make an assumption that the problem here is the subject being too hard, you won’t be able to solve the problem.

2. Defining/Understanding the Problem

It’s vital to properly define the problem once it’s been identified. Only by defining the problem, further steps can be taken to solve it. While at it, you also need to take into consideration different perspectives to understand any problem; this will also help you look for solutions with different perspectives.

Now, following up with the previous example . Let’s say you have identified the problem as not being able to allocate enough time for your studies. You need to sort out the reason behind it. Have you just been procrastinating? Have you been too busy with work? You need to understand the whole problem and reasons behind it, which is the second step in problem solving.

3. Forming a Strategy

Developing a strategy is the next step to finding a solution. Each different situation will require formulating different strategies, also depending on individual’s unique preferences.

Now, you have identified and studied your problem. You can’t just simply jump into trying to solve it. You can’t just quit work and start studying. You need to draw up a strategy to manage your time properly. Allocate less time for not-so-important works, and add them to your study time. Your strategy should be well thought, so that in theory at least, you are able to manage enough time to study properly and not fail in the exams.

4. Organizing Information

Organizing the available information is another crucial step to the process. You need to consider

• What do you know about the problem?
• What do you not know about the problem?

Accuracy of the solution for your problem will depend on the amount of information available.

The hypothetical strategy you formulate isn’t the all of it either. You need to now contemplate on the information available on the subject matter. Use the aforementioned questions to find out more about the problem. Proper organization of the information will force you to revise your strategy and refine it for best results.

5. Allocating Resources

Time, money and other resources aren’t unlimited. Deciding how high the priority is to solve your problem will help you determine the resources you’ll be using in your course to find the solution. If the problem is important, you can allocate more resources to solving it. However, if the problem isn’t as important, it’s not worth the time and money you might spend on it if not for proper planning.

For instance , let’s consider a different scenario where your business deal is stuck, but it’s few thousand miles away. Now, you need to analyze the problem and the resources you can afford to expend to solve the particular problem. If the deal isn’t really in your favor, you could just try solving it over the phone, however, more important deals might require you to fly to the location in order to solve the issue.

6. Monitoring Progress

You need to document your progress as you are finding a solution. Don’t rely on your memory, no matter how good your memory is. Effective problem-solvers have been known to monitor their progress regularly. And, if they’re not making as much progress as they’re supposed to, they will reevaluate their approach or look for new strategies.

Problem solving isn’t an overnight feat. You can’t just have a body like that of Brad Pitt after a single session in the gym. It takes time and patience. Likewise, you need to work towards solving any problem every day until you finally achieve the results. Looking back at the previous example , if everything’s according to plan, you will be allocating more and more time for your studies until finally you are confident that you’re improving. One way to make sure that you’re on a right path to solving a problem is by keeping track of the progress. To solve the problem illustrated in the first example, you can take self-tests every week or two and track your progress.

7. Evaluating the Results

Your job still isn’t done even if you’ve reached a solution. You need to evaluate the solution to find out if it’s the best possible solution to the problem. The evaluation might be immediate or might take a while. For instance , answer to a math problem can be checked then and there, however solution to your yearly tax issue might not be possible to be evaluated right there.

• Take time to identify the possible sources of the problem. It’s better to spend a substantial amount of time on something right, than on something completely opposite.
• Ask yourself questions like What, Why, How to figure out the causes of the problem. Only then can you move forward on solving it.
• Carefully outline the methods to tackle the problem. There might be different solutions to a problem, record them all.
• Gather all information about the problem and the approaches. More, the merrier.
• From the outlined methods, choose the ones that are viable to approach. Try discarding the ones that have unseen consequences.
• Track your progress as you go.
• Evaluate the outcome of the progress.

What are other people reading?

Divergent Thinking

Convergent Thinking

Convergent Vs Divergent Thinking

• Skip to main content
• Skip to primary sidebar
• Skip to footer

Psychology Spot

All About Psychology

The 5 phases of problem solving

Problem solving is a complex psychological process through which we try to find the best way to overcome an obstacle or face a challenge. Unfortunately, this process is not always linear, but can follow tortuous paths, plunging us into a situation of psychological anguish when we believe that there is no possible solution.

On the other hand, knowing the phases of problem solving will save us a lot of headaches. Providing a coherent structure to the situation that concerns us, and having a common thread that guides us along the way, will help us to put some order in the mental chaos that problems usually generate.

To Solve a Problem, Experience Does not Always Work in Our Favor

Experience can be a plus or, on the contrary, become an impediment to solving problems. Psychologists from the universities of Hong Kong and Princeton examined how we implement problem-solving strategies by asking a group of people to solve a series of problems with matches.

Participants were presented with a series of linked squares. Each square in the matrix was made up of separate pieces, and people had to remove a certain number of matches while keeping a specified number of squares intact. The interesting thing about these types of problems is that they generally have more than one solution, different strategies can be used and these must change according to the configuration of the matrix, just as it usually happens with life problems.

These researchers found that participants went through two major stages in problem solving. At first they let themselves be carried away by the perceptual characteristics of the problem and began to explore different strategies, some successful and others not.

In a second moment they used the accumulated experience to narrow their options of strategies, focusing on those that were more successful. The problem is that the more the participants trusted their strategic knowledge, the more difficulties they had in solving problems that demanded the application of novel strategies. In practice, they suffered from a kind of functional fixation.

These series of experiments show us that to solve a problem we must keep an open mind because along the way circumstances are likely to change and we need the mental flexibility necessary to change our problem-solving strategies.

The Stages of Problem Solving We Can All Apply

1. Identify the problem

It may seem like a truism, but the truth is that identifying the real problem is not as easy as it seems, especially when it comes to a situation that affects us emotionally. In fact, when the problem is too scary or we sense that we do not have the psychological tools to solve it, we usually put into practice defense mechanisms such as displacement that allow us to erase the problematic situation from our conscious mind.

Instead, being able to identify the problem is the first step in finding a solution. Many times that means stopping looking outside for the culprits and searching within, wondering why a situation is particularly bothering or hindering us.

2. Understand the problem

Many times the problem brings with it the seed of the solution. So one of the steps in solving a problem is making sure we understand it. It is not enough to identify the problem, we need to define it. For this we need to analyze it from different perspectives.

For example, if we are trying to carry out a professional project that does not finish taking off, we have to clarify the reasons. Do we need more training? Are we in an overly competitive sector? Do we have enough resources? We need to understand the source of the problem.

Organizing the information available is another crucial step in the problem-solving process. We have to ask ourselves both, what we know about the problem and everything we do not know. Ultimately, the accuracy of the solution will largely depend on the amount of information available.

3. Assume a psychological distance

Most of the major problems in life have the potential to generate an emotional tsunami. However, many times that affective involvement obfuscates and prevents us from thinking clearly. That is why on many occasions one of the most important but least known phases for solving problems consists of moving away from what concerns us. To assume a psychological distance , we can take a few days away from the problematic environment or try to stop thinking about what worries us for a while.

During that time the unconscious mind will continue to work and is likely to generate creative and perfectly valid insights that lead to the solution of the problem. That distance to allow us to overcome the functional fixations that prevent us from thinking outside the box, giving way to a mental restructuring that will allow us to see the problem from another perspective.

4. Find solutions and develop strategies

Each problem is different, so it will require a specific solution. A solution cannot always be reached by insight, so it will be necessary to think of possible alternatives to solve the problem. Synectics , for example, is a problem-solving method that uses creativity to find original solutions.

The next step is to develop a strategy, since solutions that do not materialize in concrete steps are very difficult to implement. Therefore, we must ask ourselves how we are going to implement our solution. In this phase of problem solving it is important to be honest with ourselves and “land” that strategy taking into account our resources and real availability. It is useless to develop a great strategy if we cannot apply it later.

5. Evaluation of progress

Very few problems are solved overnight. These are generally complex situations that we must patiently “unwind” over time. Therefore, another of the phases to solve a problem consists of monitoring the results that we are achieving. This way we make sure that we are on the right track and we are not wasting energy and time uselessly.

In this last stage of problem solving it is important to be able to adapt our expectations. It is difficult for a professional project to take off in the blink of an eye, so we must focus on the small steps that indicate that the solution is paying off. To do this, it is important to sit down and reflect on the impact of the solution from time to time.

We must also bear in mind that circumstances often change, so we may need to make adjustments to our initial solution. This requires great mental flexibility to change course when we realize that the strategy is not as effective as we would like.

Fedor, A. et. Al. (2015) Problem solving stages in the five square problem.  Front. Psychol ; 6: 1050.

Louis Lee, N. Y. & Johnson-Laird, P. N. (2013) Strategic changes in problem solving.  Journal of Cognitive Psychology ; 25: 165–173. 

Gillen, G. (2009) Managing Executive Function Impairments to Optimize Function.  Cognitive and Perceptual Rehabilitation ; 245-283.

Jennifer Delgado

I am a psychologist and I spent several years writing articles for scientific journals specialized in Health and Psychology. I want to help you create great experiences. Learn more about me .

What is self-efficacy and why is it essential to develop it?

20/05/2024 By Jennifer Delgado

Children’s worries are more intense than we suspect

The Illusion of Transparency: What is?

18/05/2024 By Jennifer Delgado

Definition:

Problem Solving is the process of identifying, analyzing, and finding effective solutions to complex issues or challenges.

Key Steps in Problem Solving:

• Identification of the problem: Recognizing and clearly defining the issue that needs to be resolved.
• Analysis and research: Gathering relevant information, data, and facts to understand the problem in-depth.
• Formulating strategies: Developing various approaches and plans to tackle the problem effectively.
• Evaluation and selection: Assessing the viability and potential outcomes of the proposed solutions and selecting the most appropriate one.
• Implementation: Putting the chosen solution into action and executing the necessary steps to resolve the problem.
• Monitoring and feedback: Continuously evaluating the implemented solution and obtaining feedback to ensure its effectiveness.
• Adaptation and improvement: Modifying and refining the solution as needed to optimize results and prevent similar problems from arising in the future.

Skills and Qualities for Effective Problem Solving:

• Analytical thinking: The ability to break down complex problems into smaller, manageable components and analyze them thoroughly.
• Creativity: Thinking outside the box and generating innovative solutions.
• Decision making: Making logical and informed choices based on available data and critical thinking.
• Communication: Clearly conveying ideas, listening actively, and collaborating with others to solve problems as a team.
• Resilience: Maintaining a positive mindset, perseverance, and adaptability in the face of challenges.
• Resourcefulness: Utilizing available resources and seeking new approaches when confronted with obstacles.
• Time management: Effectively organizing and prioritizing tasks to optimize problem-solving efficiency.

• Search Menu
• Browse content in Arts and Humanities
• Browse content in Archaeology
• Anglo-Saxon and Medieval Archaeology
• Archaeological Methodology and Techniques
• Archaeology by Region
• Archaeology of Religion
• Archaeology of Trade and Exchange
• Biblical Archaeology
• Contemporary and Public Archaeology
• Environmental Archaeology
• Historical Archaeology
• History and Theory of Archaeology
• Industrial Archaeology
• Landscape Archaeology
• Mortuary Archaeology
• Prehistoric Archaeology
• Underwater Archaeology
• Urban Archaeology
• Zooarchaeology
• Browse content in Architecture
• Architectural Structure and Design
• History of Architecture
• Residential and Domestic Buildings
• Theory of Architecture
• Browse content in Art
• Art Subjects and Themes
• History of Art
• Industrial and Commercial Art
• Theory of Art
• Biographical Studies
• Byzantine Studies
• Browse content in Classical Studies
• Classical History
• Classical Philosophy
• Classical Mythology
• Classical Literature
• Classical Reception
• Classical Art and Architecture
• Classical Oratory and Rhetoric
• Greek and Roman Epigraphy
• Greek and Roman Law
• Greek and Roman Papyrology
• Greek and Roman Archaeology
• Late Antiquity
• Religion in the Ancient World
• Digital Humanities
• Browse content in History
• Colonialism and Imperialism
• Diplomatic History
• Environmental History
• Genealogy, Heraldry, Names, and Honours
• Genocide and Ethnic Cleansing
• Historical Geography
• History by Period
• History of Emotions
• History of Agriculture
• History of Education
• History of Gender and Sexuality
• Industrial History
• Intellectual History
• International History
• Labour History
• Legal and Constitutional History
• Local and Family History
• Maritime History
• Military History
• National Liberation and Post-Colonialism
• Oral History
• Political History
• Public History
• Regional and National History
• Revolutions and Rebellions
• Slavery and Abolition of Slavery
• Social and Cultural History
• Theory, Methods, and Historiography
• Urban History
• World History
• Browse content in Language Teaching and Learning
• Language Learning (Specific Skills)
• Language Teaching Theory and Methods
• Browse content in Linguistics
• Applied Linguistics
• Cognitive Linguistics
• Computational Linguistics
• Forensic Linguistics
• Grammar, Syntax and Morphology
• Historical and Diachronic Linguistics
• History of English
• Language Acquisition
• Language Evolution
• Language Reference
• Language Variation
• Language Families
• Lexicography
• Linguistic Anthropology
• Linguistic Theories
• Linguistic Typology
• Phonetics and Phonology
• Psycholinguistics
• Sociolinguistics
• Translation and Interpretation
• Writing Systems
• Browse content in Literature
• Bibliography
• Children's Literature Studies
• Literary Studies (Asian)
• Literary Studies (European)
• Literary Studies (Eco-criticism)
• Literary Studies (Romanticism)
• Literary Studies (American)
• Literary Studies (Modernism)
• Literary Studies - World
• Literary Studies (1500 to 1800)
• Literary Studies (19th Century)
• Literary Studies (20th Century onwards)
• Literary Studies (African American Literature)
• Literary Studies (British and Irish)
• Literary Studies (Early and Medieval)
• Literary Studies (Fiction, Novelists, and Prose Writers)
• Literary Studies (Gender Studies)
• Literary Studies (Graphic Novels)
• Literary Studies (History of the Book)
• Literary Studies (Plays and Playwrights)
• Literary Studies (Poetry and Poets)
• Literary Studies (Postcolonial Literature)
• Literary Studies (Queer Studies)
• Literary Studies (Science Fiction)
• Literary Studies (Travel Literature)
• Literary Studies (War Literature)
• Literary Studies (Women's Writing)
• Literary Theory and Cultural Studies
• Mythology and Folklore
• Shakespeare Studies and Criticism
• Browse content in Media Studies
• Browse content in Music
• Applied Music
• Dance and Music
• Ethics in Music
• Ethnomusicology
• Gender and Sexuality in Music
• Medicine and Music
• Music Cultures
• Music and Religion
• Music and Media
• Music and Culture
• Music Education and Pedagogy
• Music Theory and Analysis
• Musical Scores, Lyrics, and Libretti
• Musical Structures, Styles, and Techniques
• Musicology and Music History
• Performance Practice and Studies
• Race and Ethnicity in Music
• Sound Studies
• Browse content in Performing Arts
• Browse content in Philosophy
• Aesthetics and Philosophy of Art
• Epistemology
• Feminist Philosophy
• History of Western Philosophy
• Metaphysics
• Moral Philosophy
• Non-Western Philosophy
• Philosophy of Science
• Philosophy of Language
• Philosophy of Mind
• Philosophy of Perception
• Philosophy of Action
• Philosophy of Law
• Philosophy of Religion
• Philosophy of Mathematics and Logic
• Practical Ethics
• Social and Political Philosophy
• Browse content in Religion
• Biblical Studies
• Christianity
• East Asian Religions
• History of Religion
• Judaism and Jewish Studies
• Qumran Studies
• Religion and Education
• Religion and Health
• Religion and Politics
• Religion and Science
• Religion and Law
• Religion and Art, Literature, and Music
• Religious Studies
• Browse content in Society and Culture
• Cookery, Food, and Drink
• Cultural Studies
• Customs and Traditions
• Ethical Issues and Debates
• Hobbies, Games, Arts and Crafts
• Lifestyle, Home, and Garden
• Natural world, Country Life, and Pets
• Popular Beliefs and Controversial Knowledge
• Sports and Outdoor Recreation
• Technology and Society
• Travel and Holiday
• Visual Culture
• Browse content in Law
• Arbitration
• Browse content in Company and Commercial Law
• Commercial Law
• Company Law
• Browse content in Comparative Law
• Systems of Law
• Competition Law
• Browse content in Constitutional and Administrative Law
• Government Powers
• Judicial Review
• Local Government Law
• Military and Defence Law
• Parliamentary and Legislative Practice
• Construction Law
• Contract Law
• Browse content in Criminal Law
• Criminal Procedure
• Criminal Evidence Law
• Sentencing and Punishment
• Employment and Labour Law
• Environment and Energy Law
• Browse content in Financial Law
• Banking Law
• Insolvency Law
• History of Law
• Human Rights and Immigration
• Intellectual Property Law
• Browse content in International Law
• Private International Law and Conflict of Laws
• Public International Law
• IT and Communications Law
• Jurisprudence and Philosophy of Law
• Law and Politics
• Law and Society
• Browse content in Legal System and Practice
• Courts and Procedure
• Legal Skills and Practice
• Primary Sources of Law
• Regulation of Legal Profession
• Medical and Healthcare Law
• Browse content in Policing
• Criminal Investigation and Detection
• Police and Security Services
• Police Procedure and Law
• Police Regional Planning
• Browse content in Property Law
• Personal Property Law
• Study and Revision
• Terrorism and National Security Law
• Browse content in Trusts Law
• Wills and Probate or Succession
• Browse content in Medicine and Health
• Browse content in Allied Health Professions
• Arts Therapies
• Clinical Science
• Dietetics and Nutrition
• Occupational Therapy
• Operating Department Practice
• Physiotherapy
• Radiography
• Speech and Language Therapy
• Browse content in Anaesthetics
• General Anaesthesia
• Neuroanaesthesia
• Browse content in Clinical Medicine
• Acute Medicine
• Cardiovascular Medicine
• Clinical Genetics
• Clinical Pharmacology and Therapeutics
• Dermatology
• Endocrinology and Diabetes
• Gastroenterology
• Genito-urinary Medicine
• Geriatric Medicine
• Infectious Diseases
• Medical Toxicology
• Medical Oncology
• Pain Medicine
• Palliative Medicine
• Rehabilitation Medicine
• Respiratory Medicine and Pulmonology
• Rheumatology
• Sleep Medicine
• Sports and Exercise Medicine
• Clinical Neuroscience
• Community Medical Services
• Critical Care
• Emergency Medicine
• Forensic Medicine
• Haematology
• History of Medicine
• Browse content in Medical Dentistry
• Oral and Maxillofacial Surgery
• Paediatric Dentistry
• Restorative Dentistry and Orthodontics
• Surgical Dentistry
• Browse content in Medical Skills
• Clinical Skills
• Communication Skills
• Nursing Skills
• Surgical Skills
• Medical Ethics
• Medical Statistics and Methodology
• Browse content in Neurology
• Clinical Neurophysiology
• Neuropathology
• Nursing Studies
• Browse content in Obstetrics and Gynaecology
• Gynaecology
• Occupational Medicine
• Ophthalmology
• Otolaryngology (ENT)
• Browse content in Paediatrics
• Neonatology
• Browse content in Pathology
• Chemical Pathology
• Clinical Cytogenetics and Molecular Genetics
• Histopathology
• Medical Microbiology and Virology
• Patient Education and Information
• Browse content in Pharmacology
• Psychopharmacology
• Browse content in Popular Health
• Caring for Others
• Complementary and Alternative Medicine
• Self-help and Personal Development
• Browse content in Preclinical Medicine
• Cell Biology
• Molecular Biology and Genetics
• Reproduction, Growth and Development
• Primary Care
• Professional Development in Medicine
• Browse content in Psychiatry
• Addiction Medicine
• Child and Adolescent Psychiatry
• Forensic Psychiatry
• Learning Disabilities
• Old Age Psychiatry
• Psychotherapy
• Browse content in Public Health and Epidemiology
• Epidemiology
• Public Health
• Browse content in Radiology
• Clinical Radiology
• Interventional Radiology
• Nuclear Medicine
• Radiation Oncology
• Reproductive Medicine
• Browse content in Surgery
• Cardiothoracic Surgery
• Gastro-intestinal and Colorectal Surgery
• General Surgery
• Neurosurgery
• Paediatric Surgery
• Peri-operative Care
• Plastic and Reconstructive Surgery
• Surgical Oncology
• Transplant Surgery
• Trauma and Orthopaedic Surgery
• Vascular Surgery
• Browse content in Science and Mathematics
• Browse content in Biological Sciences
• Aquatic Biology
• Biochemistry
• Bioinformatics and Computational Biology
• Developmental Biology
• Ecology and Conservation
• Evolutionary Biology
• Genetics and Genomics
• Microbiology
• Molecular and Cell Biology
• Natural History
• Plant Sciences and Forestry
• Research Methods in Life Sciences
• Structural Biology
• Systems Biology
• Zoology and Animal Sciences
• Browse content in Chemistry
• Analytical Chemistry
• Computational Chemistry
• Crystallography
• Environmental Chemistry
• Industrial Chemistry
• Inorganic Chemistry
• Materials Chemistry
• Medicinal Chemistry
• Mineralogy and Gems
• Organic Chemistry
• Physical Chemistry
• Polymer Chemistry
• Study and Communication Skills in Chemistry
• Theoretical Chemistry
• Browse content in Computer Science
• Artificial Intelligence
• Computer Architecture and Logic Design
• Game Studies
• Human-Computer Interaction
• Mathematical Theory of Computation
• Programming Languages
• Software Engineering
• Systems Analysis and Design
• Virtual Reality
• Browse content in Computing
• Business Applications
• Computer Security
• Computer Games
• Computer Networking and Communications
• Digital Lifestyle
• Graphical and Digital Media Applications
• Operating Systems
• Browse content in Earth Sciences and Geography
• Atmospheric Sciences
• Environmental Geography
• Geology and the Lithosphere
• Maps and Map-making
• Meteorology and Climatology
• Oceanography and Hydrology
• Palaeontology
• Physical Geography and Topography
• Regional Geography
• Soil Science
• Urban Geography
• Browse content in Engineering and Technology
• Agriculture and Farming
• Biological Engineering
• Civil Engineering, Surveying, and Building
• Electronics and Communications Engineering
• Energy Technology
• Engineering (General)
• Environmental Science, Engineering, and Technology
• History of Engineering and Technology
• Mechanical Engineering and Materials
• Technology of Industrial Chemistry
• Transport Technology and Trades
• Browse content in Environmental Science
• Applied Ecology (Environmental Science)
• Conservation of the Environment (Environmental Science)
• Environmental Sustainability
• Environmentalist Thought and Ideology (Environmental Science)
• Management of Land and Natural Resources (Environmental Science)
• Natural Disasters (Environmental Science)
• Nuclear Issues (Environmental Science)
• Pollution and Threats to the Environment (Environmental Science)
• Social Impact of Environmental Issues (Environmental Science)
• History of Science and Technology
• Browse content in Materials Science
• Ceramics and Glasses
• Composite Materials
• Metals, Alloying, and Corrosion
• Nanotechnology
• Browse content in Mathematics
• Applied Mathematics
• Biomathematics and Statistics
• History of Mathematics
• Mathematical Education
• Mathematical Finance
• Mathematical Analysis
• Numerical and Computational Mathematics
• Probability and Statistics
• Pure Mathematics
• Browse content in Neuroscience
• Cognition and Behavioural Neuroscience
• Development of the Nervous System
• Disorders of the Nervous System
• History of Neuroscience
• Invertebrate Neurobiology
• Molecular and Cellular Systems
• Neuroendocrinology and Autonomic Nervous System
• Neuroscientific Techniques
• Sensory and Motor Systems
• Browse content in Physics
• Astronomy and Astrophysics
• Atomic, Molecular, and Optical Physics
• Biological and Medical Physics
• Classical Mechanics
• Computational Physics
• Condensed Matter Physics
• Electromagnetism, Optics, and Acoustics
• History of Physics
• Mathematical and Statistical Physics
• Measurement Science
• Nuclear Physics
• Particles and Fields
• Plasma Physics
• Quantum Physics
• Relativity and Gravitation
• Semiconductor and Mesoscopic Physics
• Browse content in Psychology
• Affective Sciences
• Clinical Psychology
• Cognitive Psychology
• Cognitive Neuroscience
• Criminal and Forensic Psychology
• Developmental Psychology
• Educational Psychology
• Evolutionary Psychology
• Health Psychology
• History and Systems in Psychology
• Music Psychology
• Neuropsychology
• Organizational Psychology
• Psychological Assessment and Testing
• Psychology of Human-Technology Interaction
• Psychology Professional Development and Training
• Research Methods in Psychology
• Social Psychology
• Browse content in Social Sciences
• Browse content in Anthropology
• Anthropology of Religion
• Human Evolution
• Medical Anthropology
• Physical Anthropology
• Regional Anthropology
• Social and Cultural Anthropology
• Theory and Practice of Anthropology
• Browse content in Business and Management
• Business Strategy
• Business Ethics
• Business History
• Business and Government
• Business and Technology
• Business and the Environment
• Comparative Management
• Corporate Governance
• Corporate Social Responsibility
• Entrepreneurship
• Health Management
• Human Resource Management
• Industrial and Employment Relations
• Industry Studies
• Information and Communication Technologies
• International Business
• Knowledge Management
• Management and Management Techniques
• Operations Management
• Organizational Theory and Behaviour
• Pensions and Pension Management
• Public and Nonprofit Management
• Strategic Management
• Supply Chain Management
• Browse content in Criminology and Criminal Justice
• Criminal Justice
• Criminology
• Forms of Crime
• International and Comparative Criminology
• Youth Violence and Juvenile Justice
• Development Studies
• Browse content in Economics
• Agricultural, Environmental, and Natural Resource Economics
• Asian Economics
• Behavioural Finance
• Behavioural Economics and Neuroeconomics
• Econometrics and Mathematical Economics
• Economic Systems
• Economic History
• Economic Methodology
• Economic Development and Growth
• Financial Markets
• Financial Institutions and Services
• General Economics and Teaching
• Health, Education, and Welfare
• History of Economic Thought
• International Economics
• Labour and Demographic Economics
• Law and Economics
• Macroeconomics and Monetary Economics
• Microeconomics
• Public Economics
• Urban, Rural, and Regional Economics
• Welfare Economics
• Browse content in Education
• Adult Education and Continuous Learning
• Care and Counselling of Students
• Early Childhood and Elementary Education
• Educational Equipment and Technology
• Educational Strategies and Policy
• Higher and Further Education
• Organization and Management of Education
• Philosophy and Theory of Education
• Schools Studies
• Secondary Education
• Teaching of a Specific Subject
• Teaching of Specific Groups and Special Educational Needs
• Teaching Skills and Techniques
• Browse content in Environment
• Applied Ecology (Social Science)
• Climate Change
• Conservation of the Environment (Social Science)
• Environmentalist Thought and Ideology (Social Science)
• Natural Disasters (Environment)
• Social Impact of Environmental Issues (Social Science)
• Browse content in Human Geography
• Cultural Geography
• Economic Geography
• Political Geography
• Browse content in Interdisciplinary Studies
• Communication Studies
• Museums, Libraries, and Information Sciences
• Browse content in Politics
• African Politics
• Asian Politics
• Chinese Politics
• Comparative Politics
• Conflict Politics
• Elections and Electoral Studies
• Environmental Politics
• European Union
• Foreign Policy
• Gender and Politics
• Human Rights and Politics
• Indian Politics
• International Relations
• International Organization (Politics)
• International Political Economy
• Irish Politics
• Latin American Politics
• Middle Eastern Politics
• Political Methodology
• Political Communication
• Political Philosophy
• Political Sociology
• Political Behaviour
• Political Economy
• Political Institutions
• Political Theory
• Politics and Law
• Public Administration
• Public Policy
• Quantitative Political Methodology
• Regional Political Studies
• Russian Politics
• Security Studies
• State and Local Government
• UK Politics
• US Politics
• Browse content in Regional and Area Studies
• African Studies
• Asian Studies
• East Asian Studies
• Japanese Studies
• Latin American Studies
• Middle Eastern Studies
• Native American Studies
• Scottish Studies
• Browse content in Research and Information
• Research Methods
• Browse content in Social Work
• Addictions and Substance Misuse
• Adoption and Fostering
• Care of the Elderly
• Child and Adolescent Social Work
• Couple and Family Social Work
• Developmental and Physical Disabilities Social Work
• Direct Practice and Clinical Social Work
• Emergency Services
• Human Behaviour and the Social Environment
• International and Global Issues in Social Work
• Mental and Behavioural Health
• Social Justice and Human Rights
• Social Policy and Advocacy
• Social Work and Crime and Justice
• Social Work Macro Practice
• Social Work Practice Settings
• Social Work Research and Evidence-based Practice
• Welfare and Benefit Systems
• Browse content in Sociology
• Childhood Studies
• Community Development
• Comparative and Historical Sociology
• Economic Sociology
• Gender and Sexuality
• Gerontology and Ageing
• Health, Illness, and Medicine
• Marriage and the Family
• Migration Studies
• Occupations, Professions, and Work
• Organizations
• Population and Demography
• Race and Ethnicity
• Social Theory
• Social Movements and Social Change
• Social Research and Statistics
• Social Stratification, Inequality, and Mobility
• Sociology of Religion
• Sociology of Education
• Sport and Leisure
• Urban and Rural Studies
• Browse content in Warfare and Defence
• Defence Strategy, Planning, and Research
• Land Forces and Warfare
• Military Administration
• Military Life and Institutions
• Naval Forces and Warfare
• Other Warfare and Defence Issues
• Peace Studies and Conflict Resolution
• Weapons and Equipment

• < Previous chapter
• Next chapter >

48 Problem Solving

Department of Psychological and Brain Sciences, University of California, Santa Barbara

• Published: 03 June 2013
• Cite Icon Cite
• Permissions Icon Permissions

Problem solving refers to cognitive processing directed at achieving a goal when the problem solver does not initially know a solution method. A problem exists when someone has a goal but does not know how to achieve it. Problems can be classified as routine or nonroutine, and as well defined or ill defined. The major cognitive processes in problem solving are representing, planning, executing, and monitoring. The major kinds of knowledge required for problem solving are facts, concepts, procedures, strategies, and beliefs. Classic theoretical approaches to the study of problem solving are associationism, Gestalt, and information processing. Current issues and suggested future issues include decision making, intelligence and creativity, teaching of thinking skills, expert problem solving, analogical reasoning, mathematical and scientific thinking, everyday thinking, and the cognitive neuroscience of problem solving. Common themes concern the domain specificity of problem solving and a focus on problem solving in authentic contexts.

The study of problem solving begins with defining problem solving, problem, and problem types. This introduction to problem solving is rounded out with an examination of cognitive processes in problem solving, the role of knowledge in problem solving, and historical approaches to the study of problem solving.

Definition of Problem Solving

Problem solving refers to cognitive processing directed at achieving a goal for which the problem solver does not initially know a solution method. This definition consists of four major elements (Mayer, 1992 ; Mayer & Wittrock, 2006 ):

Cognitive —Problem solving occurs within the problem solver’s cognitive system and can only be inferred indirectly from the problem solver’s behavior (including biological changes, introspections, and actions during problem solving). Process —Problem solving involves mental computations in which some operation is applied to a mental representation, sometimes resulting in the creation of a new mental representation. Directed —Problem solving is aimed at achieving a goal. Personal —Problem solving depends on the existing knowledge of the problem solver so that what is a problem for one problem solver may not be a problem for someone who already knows a solution method.

The definition is broad enough to include a wide array of cognitive activities such as deciding which apartment to rent, figuring out how to use a cell phone interface, playing a game of chess, making a medical diagnosis, finding the answer to an arithmetic word problem, or writing a chapter for a handbook. Problem solving is pervasive in human life and is crucial for human survival. Although this chapter focuses on problem solving in humans, problem solving also occurs in nonhuman animals and in intelligent machines.

How is problem solving related to other forms of high-level cognition processing, such as thinking and reasoning? Thinking refers to cognitive processing in individuals but includes both directed thinking (which corresponds to the definition of problem solving) and undirected thinking such as daydreaming (which does not correspond to the definition of problem solving). Thus, problem solving is a type of thinking (i.e., directed thinking).

Reasoning refers to problem solving within specific classes of problems, such as deductive reasoning or inductive reasoning. In deductive reasoning, the reasoner is given premises and must derive a conclusion by applying the rules of logic. For example, given that “A is greater than B” and “B is greater than C,” a reasoner can conclude that “A is greater than C.” In inductive reasoning, the reasoner is given (or has experienced) a collection of examples or instances and must infer a rule. For example, given that X, C, and V are in the “yes” group and x, c, and v are in the “no” group, the reasoning may conclude that B is in “yes” group because it is in uppercase format. Thus, reasoning is a type of problem solving.

Definition of Problem

A problem occurs when someone has a goal but does not know to achieve it. This definition is consistent with how the Gestalt psychologist Karl Duncker ( 1945 , p. 1) defined a problem in his classic monograph, On Problem Solving : “A problem arises when a living creature has a goal but does not know how this goal is to be reached.” However, today researchers recognize that the definition should be extended to include problem solving by intelligent machines. This definition can be clarified using an information processing approach by noting that a problem occurs when a situation is in the given state, the problem solver wants the situation to be in the goal state, and there is no obvious way to move from the given state to the goal state (Newell & Simon, 1972 ). Accordingly, the three main elements in describing a problem are the given state (i.e., the current state of the situation), the goal state (i.e., the desired state of the situation), and the set of allowable operators (i.e., the actions the problem solver is allowed to take). The definition of “problem” is broad enough to include the situation confronting a physician who wishes to make a diagnosis on the basis of preliminary tests and a patient examination, as well as a beginning physics student trying to solve a complex physics problem.

Types of Problems

It is customary in the problem-solving literature to make a distinction between routine and nonroutine problems. Routine problems are problems that are so familiar to the problem solver that the problem solver knows a solution method. For example, for most adults, “What is 365 divided by 12?” is a routine problem because they already know the procedure for long division. Nonroutine problems are so unfamiliar to the problem solver that the problem solver does not know a solution method. For example, figuring out the best way to set up a funding campaign for a nonprofit charity is a nonroutine problem for most volunteers. Technically, routine problems do not meet the definition of problem because the problem solver has a goal but knows how to achieve it. Much research on problem solving has focused on routine problems, although most interesting problems in life are nonroutine.

Another customary distinction is between well-defined and ill-defined problems. Well-defined problems have a clearly specified given state, goal state, and legal operators. Examples include arithmetic computation problems or games such as checkers or tic-tac-toe. Ill-defined problems have a poorly specified given state, goal state, or legal operators, or a combination of poorly defined features. Examples include solving the problem of global warming or finding a life partner. Although, ill-defined problems are more challenging, much research in problem solving has focused on well-defined problems.

Cognitive Processes in Problem Solving

The process of problem solving can be broken down into two main phases: problem representation , in which the problem solver builds a mental representation of the problem situation, and problem solution , in which the problem solver works to produce a solution. The major subprocess in problem representation is representing , which involves building a situation model —that is, a mental representation of the situation described in the problem. The major subprocesses in problem solution are planning , which involves devising a plan for how to solve the problem; executing , which involves carrying out the plan; and monitoring , which involves evaluating and adjusting one’s problem solving.

For example, given an arithmetic word problem such as “Alice has three marbles. Sarah has two more marbles than Alice. How many marbles does Sarah have?” the process of representing involves building a situation model in which Alice has a set of marbles, there is set of marbles for the difference between the two girls, and Sarah has a set of marbles that consists of Alice’s marbles and the difference set. In the planning process, the problem solver sets a goal of adding 3 and 2. In the executing process, the problem solver carries out the computation, yielding an answer of 5. In the monitoring process, the problem solver looks over what was done and concludes that 5 is a reasonable answer. In most complex problem-solving episodes, the four cognitive processes may not occur in linear order, but rather may interact with one another. Although some research focuses mainly on the execution process, problem solvers may tend to have more difficulty with the processes of representing, planning, and monitoring.

Knowledge for Problem Solving

An important theme in problem-solving research is that problem-solving proficiency on any task depends on the learner’s knowledge (Anderson et al., 2001 ; Mayer, 1992 ). Five kinds of knowledge are as follows:

Facts —factual knowledge about the characteristics of elements in the world, such as “Sacramento is the capital of California” Concepts —conceptual knowledge, including categories, schemas, or models, such as knowing the difference between plants and animals or knowing how a battery works Procedures —procedural knowledge of step-by-step processes, such as how to carry out long-division computations Strategies —strategic knowledge of general methods such as breaking a problem into parts or thinking of a related problem Beliefs —attitudinal knowledge about how one’s cognitive processing works such as thinking, “I’m good at this”

Although some research focuses mainly on the role of facts and procedures in problem solving, complex problem solving also depends on the problem solver’s concepts, strategies, and beliefs (Mayer, 1992 ).

Historical Approaches to Problem Solving

Psychological research on problem solving began in the early 1900s, as an outgrowth of mental philosophy (Humphrey, 1963 ; Mandler & Mandler, 1964 ). Throughout the 20th century four theoretical approaches developed: early conceptions, associationism, Gestalt psychology, and information processing.

Early Conceptions

The start of psychology as a science can be set at 1879—the year Wilhelm Wundt opened the first world’s psychology laboratory in Leipzig, Germany, and sought to train the world’s first cohort of experimental psychologists. Instead of relying solely on philosophical speculations about how the human mind works, Wundt sought to apply the methods of experimental science to issues addressed in mental philosophy. His theoretical approach became structuralism —the analysis of consciousness into its basic elements.

Wundt’s main contribution to the study of problem solving, however, was to call for its banishment. According to Wundt, complex cognitive processing was too complicated to be studied by experimental methods, so “nothing can be discovered in such experiments” (Wundt, 1911/1973 ). Despite his admonishments, however, a group of his former students began studying thinking mainly in Wurzburg, Germany. Using the method of introspection, subjects were asked to describe their thought process as they solved word association problems, such as finding the superordinate of “newspaper” (e.g., an answer is “publication”). Although the Wurzburg group—as they came to be called—did not produce a new theoretical approach, they found empirical evidence that challenged some of the key assumptions of mental philosophy. For example, Aristotle had proclaimed that all thinking involves mental imagery, but the Wurzburg group was able to find empirical evidence for imageless thought .

Associationism

The first major theoretical approach to take hold in the scientific study of problem solving was associationism —the idea that the cognitive representations in the mind consist of ideas and links between them and that cognitive processing in the mind involves following a chain of associations from one idea to the next (Mandler & Mandler, 1964 ; Mayer, 1992 ). For example, in a classic study, E. L. Thorndike ( 1911 ) placed a hungry cat in what he called a puzzle box—a wooden crate in which pulling a loop of string that hung from overhead would open a trap door to allow the cat to escape to a bowl of food outside the crate. Thorndike placed the cat in the puzzle box once a day for several weeks. On the first day, the cat engaged in many extraneous behaviors such as pouncing against the wall, pushing its paws through the slats, and meowing, but on successive days the number of extraneous behaviors tended to decrease. Overall, the time required to get out of the puzzle box decreased over the course of the experiment, indicating the cat was learning how to escape.

Thorndike’s explanation for how the cat learned to solve the puzzle box problem is based on an associationist view: The cat begins with a habit family hierarchy —a set of potential responses (e.g., pouncing, thrusting, meowing, etc.) all associated with the same stimulus (i.e., being hungry and confined) and ordered in terms of strength of association. When placed in the puzzle box, the cat executes its strongest response (e.g., perhaps pouncing against the wall), but when it fails, the strength of the association is weakened, and so on for each unsuccessful action. Eventually, the cat gets down to what was initially a weak response—waving its paw in the air—but when that response leads to accidentally pulling the string and getting out, it is strengthened. Over the course of many trials, the ineffective responses become weak and the successful response becomes strong. Thorndike refers to this process as the law of effect : Responses that lead to dissatisfaction become less associated with the situation and responses that lead to satisfaction become more associated with the situation. According to Thorndike’s associationist view, solving a problem is simply a matter of trial and error and accidental success. A major challenge to assocationist theory concerns the nature of transfer—that is, where does a problem solver find a creative solution that has never been performed before? Associationist conceptions of cognition can be seen in current research, including neural networks, connectionist models, and parallel distributed processing models (Rogers & McClelland, 2004 ).

Gestalt Psychology

The Gestalt approach to problem solving developed in the 1930s and 1940s as a counterbalance to the associationist approach. According to the Gestalt approach, cognitive representations consist of coherent structures (rather than individual associations) and the cognitive process of problem solving involves building a coherent structure (rather than strengthening and weakening of associations). For example, in a classic study, Kohler ( 1925 ) placed a hungry ape in a play yard that contained several empty shipping crates and a banana attached overhead but out of reach. Based on observing the ape in this situation, Kohler noted that the ape did not randomly try responses until one worked—as suggested by Thorndike’s associationist view. Instead, the ape stood under the banana, looked up at it, looked at the crates, and then in a flash of insight stacked the crates under the bananas as a ladder, and walked up the steps in order to reach the banana.

According to Kohler, the ape experienced a sudden visual reorganization in which the elements in the situation fit together in a way to solve the problem; that is, the crates could become a ladder that reduces the distance to the banana. Kohler referred to the underlying mechanism as insight —literally seeing into the structure of the situation. A major challenge of Gestalt theory is its lack of precision; for example, naming a process (i.e., insight) is not the same as explaining how it works. Gestalt conceptions can be seen in modern research on mental models and schemas (Gentner & Stevens, 1983 ).

Information Processing

The information processing approach to problem solving developed in the 1960s and 1970s and was based on the influence of the computer metaphor—the idea that humans are processors of information (Mayer, 2009 ). According to the information processing approach, problem solving involves a series of mental computations—each of which consists of applying a process to a mental representation (such as comparing two elements to determine whether they differ).

In their classic book, Human Problem Solving , Newell and Simon ( 1972 ) proposed that problem solving involved a problem space and search heuristics . A problem space is a mental representation of the initial state of the problem, the goal state of the problem, and all possible intervening states (based on applying allowable operators). Search heuristics are strategies for moving through the problem space from the given to the goal state. Newell and Simon focused on means-ends analysis , in which the problem solver continually sets goals and finds moves to accomplish goals.

Newell and Simon used computer simulation as a research method to test their conception of human problem solving. First, they asked human problem solvers to think aloud as they solved various problems such as logic problems, chess, and cryptarithmetic problems. Then, based on an information processing analysis, Newell and Simon created computer programs that solved these problems. In comparing the solution behavior of humans and computers, they found high similarity, suggesting that the computer programs were solving problems using the same thought processes as humans.

An important advantage of the information processing approach is that problem solving can be described with great clarity—as a computer program. An important limitation of the information processing approach is that it is most useful for describing problem solving for well-defined problems rather than ill-defined problems. The information processing conception of cognition lives on as a keystone of today’s cognitive science (Mayer, 2009 ).

Classic Issues in Problem Solving

Three classic issues in research on problem solving concern the nature of transfer (suggested by the associationist approach), the nature of insight (suggested by the Gestalt approach), and the role of problem-solving heuristics (suggested by the information processing approach).

Transfer refers to the effects of prior learning on new learning (or new problem solving). Positive transfer occurs when learning A helps someone learn B. Negative transfer occurs when learning A hinders someone from learning B. Neutral transfer occurs when learning A has no effect on learning B. Positive transfer is a central goal of education, but research shows that people often do not transfer what they learned to solving problems in new contexts (Mayer, 1992 ; Singley & Anderson, 1989 ).

Three conceptions of the mechanisms underlying transfer are specific transfer , general transfer , and specific transfer of general principles . Specific transfer refers to the idea that learning A will help someone learn B only if A and B have specific elements in common. For example, learning Spanish may help someone learn Latin because some of the vocabulary words are similar and the verb conjugation rules are similar. General transfer refers to the idea that learning A can help someone learn B even they have nothing specifically in common but A helps improve the learner’s mind in general. For example, learning Latin may help people learn “proper habits of mind” so they are better able to learn completely unrelated subjects as well. Specific transfer of general principles is the idea that learning A will help someone learn B if the same general principle or solution method is required for both even if the specific elements are different.

In a classic study, Thorndike and Woodworth ( 1901 ) found that students who learned Latin did not subsequently learn bookkeeping any better than students who had not learned Latin. They interpreted this finding as evidence for specific transfer—learning A did not transfer to learning B because A and B did not have specific elements in common. Modern research on problem-solving transfer continues to show that people often do not demonstrate general transfer (Mayer, 1992 ). However, it is possible to teach people a general strategy for solving a problem, so that when they see a new problem in a different context they are able to apply the strategy to the new problem (Judd, 1908 ; Mayer, 2008 )—so there is also research support for the idea of specific transfer of general principles.

Insight refers to a change in a problem solver’s mind from not knowing how to solve a problem to knowing how to solve it (Mayer, 1995 ; Metcalfe & Wiebe, 1987 ). In short, where does the idea for a creative solution come from? A central goal of problem-solving research is to determine the mechanisms underlying insight.

The search for insight has led to five major (but not mutually exclusive) explanatory mechanisms—insight as completing a schema, insight as suddenly reorganizing visual information, insight as reformulation of a problem, insight as removing mental blocks, and insight as finding a problem analog (Mayer, 1995 ). Completing a schema is exemplified in a study by Selz (Fridja & de Groot, 1982 ), in which people were asked to think aloud as they solved word association problems such as “What is the superordinate for newspaper?” To solve the problem, people sometimes thought of a coordinate, such as “magazine,” and then searched for a superordinate category that subsumed both terms, such as “publication.” According to Selz, finding a solution involved building a schema that consisted of a superordinate and two subordinate categories.

Reorganizing visual information is reflected in Kohler’s ( 1925 ) study described in a previous section in which a hungry ape figured out how to stack boxes as a ladder to reach a banana hanging above. According to Kohler, the ape looked around the yard and found the solution in a flash of insight by mentally seeing how the parts could be rearranged to accomplish the goal.

Reformulating a problem is reflected in a classic study by Duncker ( 1945 ) in which people are asked to think aloud as they solve the tumor problem—how can you destroy a tumor in a patient without destroying surrounding healthy tissue by using rays that at sufficient intensity will destroy any tissue in their path? In analyzing the thinking-aloud protocols—that is, transcripts of what the problem solvers said—Duncker concluded that people reformulated the goal in various ways (e.g., avoid contact with healthy tissue, immunize healthy tissue, have ray be weak in healthy tissue) until they hit upon a productive formulation that led to the solution (i.e., concentrating many weak rays on the tumor).

Removing mental blocks is reflected in classic studies by Duncker ( 1945 ) in which solving a problem involved thinking of a novel use for an object, and by Luchins ( 1942 ) in which solving a problem involved not using a procedure that had worked well on previous problems. Finding a problem analog is reflected in classic research by Wertheimer ( 1959 ) in which learning to find the area of a parallelogram is supported by the insight that one could cut off the triangle on one side and place it on the other side to form a rectangle—so a parallelogram is really a rectangle in disguise. The search for insight along each of these five lines continues in current problem-solving research.

Heuristics are problem-solving strategies, that is, general approaches to how to solve problems. Newell and Simon ( 1972 ) suggested three general problem-solving heuristics for moving from a given state to a goal state: random trial and error , hill climbing , and means-ends analysis . Random trial and error involves randomly selecting a legal move and applying it to create a new problem state, and repeating that process until the goal state is reached. Random trial and error may work for simple problems but is not efficient for complex ones. Hill climbing involves selecting the legal move that moves the problem solver closer to the goal state. Hill climbing will not work for problems in which the problem solver must take a move that temporarily moves away from the goal as is required in many problems.

Means-ends analysis involves creating goals and seeking moves that can accomplish the goal. If a goal cannot be directly accomplished, a subgoal is created to remove one or more obstacles. Newell and Simon ( 1972 ) successfully used means-ends analysis as the search heuristic in a computer program aimed at general problem solving, that is, solving a diverse collection of problems. However, people may also use specific heuristics that are designed to work for specific problem-solving situations (Gigerenzer, Todd, & ABC Research Group, 1999 ; Kahneman & Tversky, 1984 ).

Current and Future Issues in Problem Solving

Eight current issues in problem solving involve decision making, intelligence and creativity, teaching of thinking skills, expert problem solving, analogical reasoning, mathematical and scientific problem solving, everyday thinking, and the cognitive neuroscience of problem solving.

Decision Making

Decision making refers to the cognitive processing involved in choosing between two or more alternatives (Baron, 2000 ; Markman & Medin, 2002 ). For example, a decision-making task may involve choosing between getting $240 for sure or having a 25% change of getting $1000. According to economic theories such as expected value theory, people should chose the second option, which is worth $250 (i.e., .25 x $1000) rather than the first option, which is worth $240 (1.00 x $240), but psychological research shows that most people prefer the first option (Kahneman & Tversky, 1984 ).

Research on decision making has generated three classes of theories (Markman & Medin, 2002 ): descriptive theories, such as prospect theory (Kahneman & Tversky), which are based on the ideas that people prefer to overweight the cost of a loss and tend to overestimate small probabilities; heuristic theories, which are based on the idea that people use a collection of short-cut strategies such as the availability heuristic (Gigerenzer et al., 1999 ; Kahneman & Tversky, 2000 ); and constructive theories, such as mental accounting (Kahneman & Tversky, 2000 ), in which people build a narrative to justify their choices to themselves. Future research is needed to examine decision making in more realistic settings.

Intelligence and Creativity

Although researchers do not have complete consensus on the definition of intelligence (Sternberg, 1990 ), it is reasonable to view intelligence as the ability to learn or adapt to new situations. Fluid intelligence refers to the potential to solve problems without any relevant knowledge, whereas crystallized intelligence refers to the potential to solve problems based on relevant prior knowledge (Sternberg & Gregorenko, 2003 ). As people gain more experience in a field, their problem-solving performance depends more on crystallized intelligence (i.e., domain knowledge) than on fluid intelligence (i.e., general ability) (Sternberg & Gregorenko, 2003 ). The ability to monitor and manage one’s cognitive processing during problem solving—which can be called metacognition —is an important aspect of intelligence (Sternberg, 1990 ). Research is needed to pinpoint the knowledge that is needed to support intelligent performance on problem-solving tasks.

Creativity refers to the ability to generate ideas that are original (i.e., other people do not think of the same idea) and functional (i.e., the idea works; Sternberg, 1999 ). Creativity is often measured using tests of divergent thinking —that is, generating as many solutions as possible for a problem (Guilford, 1967 ). For example, the uses test asks people to list as many uses as they can think of for a brick. Creativity is different from intelligence, and it is at the heart of creative problem solving—generating a novel solution to a problem that the problem solver has never seen before. An important research question concerns whether creative problem solving depends on specific knowledge or creativity ability in general.

Teaching of Thinking Skills

How can people learn to be better problem solvers? Mayer ( 2008 ) proposes four questions concerning teaching of thinking skills:

What to teach —Successful programs attempt to teach small component skills (such as how to generate and evaluate hypotheses) rather than improve the mind as a single monolithic skill (Covington, Crutchfield, Davies, & Olton, 1974 ). How to teach —Successful programs focus on modeling the process of problem solving rather than solely reinforcing the product of problem solving (Bloom & Broder, 1950 ). Where to teach —Successful programs teach problem-solving skills within the specific context they will be used rather than within a general course on how to solve problems (Nickerson, 1999 ). When to teach —Successful programs teaching higher order skills early rather than waiting until lower order skills are completely mastered (Tharp & Gallimore, 1988 ).

Overall, research on teaching of thinking skills points to the domain specificity of problem solving; that is, successful problem solving depends on the problem solver having domain knowledge that is relevant to the problem-solving task.

Expert Problem Solving

Research on expertise is concerned with differences between how experts and novices solve problems (Ericsson, Feltovich, & Hoffman, 2006 ). Expertise can be defined in terms of time (e.g., 10 years of concentrated experience in a field), performance (e.g., earning a perfect score on an assessment), or recognition (e.g., receiving a Nobel Prize or becoming Grand Master in chess). For example, in classic research conducted in the 1940s, de Groot ( 1965 ) found that chess experts did not have better general memory than chess novices, but they did have better domain-specific memory for the arrangement of chess pieces on the board. Chase and Simon ( 1973 ) replicated this result in a better controlled experiment. An explanation is that experts have developed schemas that allow them to chunk collections of pieces into a single configuration.

In another landmark study, Larkin et al. ( 1980 ) compared how experts (e.g., physics professors) and novices (e.g., first-year physics students) solved textbook physics problems about motion. Experts tended to work forward from the given information to the goal, whereas novices tended to work backward from the goal to the givens using a means-ends analysis strategy. Experts tended to store their knowledge in an integrated way, whereas novices tended to store their knowledge in isolated fragments. In another study, Chi, Feltovich, and Glaser ( 1981 ) found that experts tended to focus on the underlying physics concepts (such as conservation of energy), whereas novices tended to focus on the surface features of the problem (such as inclined planes or springs). Overall, research on expertise is useful in pinpointing what experts know that is different from what novices know. An important theme is that experts rely on domain-specific knowledge rather than solely general cognitive ability.

Analogical Reasoning

Analogical reasoning occurs when people solve one problem by using their knowledge about another problem (Holyoak, 2005 ). For example, suppose a problem solver learns how to solve a problem in one context using one solution method and then is given a problem in another context that requires the same solution method. In this case, the problem solver must recognize that the new problem has structural similarity to the old problem (i.e., it may be solved by the same method), even though they do not have surface similarity (i.e., the cover stories are different). Three steps in analogical reasoning are recognizing —seeing that a new problem is similar to a previously solved problem; abstracting —finding the general method used to solve the old problem; and mapping —using that general method to solve the new problem.

Research on analogical reasoning shows that people often do not recognize that a new problem can be solved by the same method as a previously solved problem (Holyoak, 2005 ). However, research also shows that successful analogical transfer to a new problem is more likely when the problem solver has experience with two old problems that have the same underlying structural features (i.e., they are solved by the same principle) but different surface features (i.e., they have different cover stories) (Holyoak, 2005 ). This finding is consistent with the idea of specific transfer of general principles as described in the section on “Transfer.”

Mathematical and Scientific Problem Solving

Research on mathematical problem solving suggests that five kinds of knowledge are needed to solve arithmetic word problems (Mayer, 2008 ):

Factual knowledge —knowledge about the characteristics of problem elements, such as knowing that there are 100 cents in a dollar Schematic knowledge —knowledge of problem types, such as being able to recognize time-rate-distance problems Strategic knowledge —knowledge of general methods, such as how to break a problem into parts Procedural knowledge —knowledge of processes, such as how to carry our arithmetic operations Attitudinal knowledge —beliefs about one’s mathematical problem-solving ability, such as thinking, “I am good at this”

People generally possess adequate procedural knowledge but may have difficulty in solving mathematics problems because they lack factual, schematic, strategic, or attitudinal knowledge (Mayer, 2008 ). Research is needed to pinpoint the role of domain knowledge in mathematical problem solving.

Research on scientific problem solving shows that people harbor misconceptions, such as believing that a force is needed to keep an object in motion (McCloskey, 1983 ). Learning to solve science problems involves conceptual change, in which the problem solver comes to recognize that previous conceptions are wrong (Mayer, 2008 ). Students can be taught to engage in scientific reasoning such as hypothesis testing through direct instruction in how to control for variables (Chen & Klahr, 1999 ). A central theme of research on scientific problem solving concerns the role of domain knowledge.

Everyday Thinking

Everyday thinking refers to problem solving in the context of one’s life outside of school. For example, children who are street vendors tend to use different procedures for solving arithmetic problems when they are working on the streets than when they are in school (Nunes, Schlieman, & Carraher, 1993 ). This line of research highlights the role of situated cognition —the idea that thinking always is shaped by the physical and social context in which it occurs (Robbins & Aydede, 2009 ). Research is needed to determine how people solve problems in authentic contexts.

Cognitive Neuroscience of Problem Solving

The cognitive neuroscience of problem solving is concerned with the brain activity that occurs during problem solving. For example, using fMRI brain imaging methodology, Goel ( 2005 ) found that people used the language areas of the brain to solve logical reasoning problems presented in sentences (e.g., “All dogs are pets…”) and used the spatial areas of the brain to solve logical reasoning problems presented in abstract letters (e.g., “All D are P…”). Cognitive neuroscience holds the potential to make unique contributions to the study of problem solving.

Problem solving has always been a topic at the fringe of cognitive psychology—too complicated to study intensively but too important to completely ignore. Problem solving—especially in realistic environments—is messy in comparison to studying elementary processes in cognition. The field remains fragmented in the sense that topics such as decision making, reasoning, intelligence, expertise, mathematical problem solving, everyday thinking, and the like are considered to be separate topics, each with its own separate literature. Yet some recurring themes are the role of domain-specific knowledge in problem solving and the advantages of studying problem solving in authentic contexts.

Future Directions

Some important issues for future research include the three classic issues examined in this chapter—the nature of problem-solving transfer (i.e., How are people able to use what they know about previous problem solving to help them in new problem solving?), the nature of insight (e.g., What is the mechanism by which a creative solution is constructed?), and heuristics (e.g., What are some teachable strategies for problem solving?). In addition, future research in problem solving should continue to pinpoint the role of domain-specific knowledge in problem solving, the nature of cognitive ability in problem solving, how to help people develop proficiency in solving problems, and how to provide aids for problem solving.

Anderson L. W. , Krathwohl D. R. , Airasian P. W. , Cruikshank K. A. , Mayer R. E. , Pintrich P. R. , Raths, J., & Wittrock M. C. ( 2001 ). A taxonomy for learning, teaching, and assessing: A revision of Bloom’s taxonomy of educational objectives. New York : Longman.

Baron J. ( 2000 ). Thinking and deciding (3rd ed.). New York : Cambridge University Press.

Google Scholar

Google Preview

Bloom B. S. , & Broder B. J. ( 1950 ). Problem-solving processes of college students: An exploratory investigation. Chicago : University of Chicago Press.

Chase W. G. , & Simon H. A. ( 1973 ). Perception in chess.   Cognitive Psychology, 4, 55–81.

Chen Z. , & Klahr D. ( 1999 ). All other things being equal: Acquisition and transfer of the control of variable strategy . Child Development, 70, 1098–1120.

Chi M. T. H. , Feltovich P. J. , & Glaser R. ( 1981 ). Categorization and representation of physics problems by experts and novices. Cognitive Science, 5, 121–152.

Covington M. V. , Crutchfield R. S. , Davies L. B. , & Olton R. M. ( 1974 ). The productive thinking program. Columbus, OH : Merrill.

de Groot A. D. ( 1965 ). Thought and choice in chess. The Hague, The Netherlands : Mouton.

Duncker K. ( 1945 ). On problem solving.   Psychological Monographs, 58 (3) (Whole No. 270).

Ericsson K. A. , Feltovich P. J. , & Hoffman R. R. (Eds.). ( 2006 ). The Cambridge handbook of expertise and expert performance. New York : Cambridge University Press.

Fridja N. H. , & de Groot A. D. ( 1982 ). Otto Selz: His contribution to psychology. The Hague, The Netherlands : Mouton.

Gentner D. , & Stevens A. L. (Eds.). ( 1983 ). Mental models. Hillsdale, NJ : Erlbaum.

Gigerenzer G. , Todd P. M. , & ABC Research Group (Eds.). ( 1999 ). Simple heuristics that make us smart. Oxford, England : Oxford University Press.

Goel V. ( 2005 ). Cognitive neuroscience of deductive reasoning. In K. J. Holyoak & R. G. Morrison (Eds.), The Cambridge handbook of thinking and reasoning (pp. 475–492). New York : Cambridge University Press.

Guilford J. P. ( 1967 ). The nature of human intelligence. New York : McGraw-Hill.

Holyoak K. J. ( 2005 ). Analogy. In K. J. Holyoak & R. G. Morrison (Eds.), The Cambridge handbook of thinking and reasoning (pp. 117–142). New York : Cambridge University Press.

Humphrey G. ( 1963 ). Thinking: An introduction to experimental psychology. New York : Wiley.

Judd C. H. ( 1908 ). The relation of special training and general intelligence. Educational Review, 36, 28–42.

Kahneman D. , & Tversky A. ( 1984 ). Choices, values, and frames. American Psychologist, 39, 341–350.

Kahneman D. , & Tversky A. (Eds.). ( 2000 ). Choices, values, and frames. New York : Cambridge University Press.

Kohler W. ( 1925 ). The mentality of apes. New York : Liveright.

Larkin J. H. , McDermott J. , Simon D. P. , & Simon H. A. ( 1980 ). Expert and novice performance in solving physics problems. Science, 208, 1335–1342.

Luchins A. ( 1942 ). Mechanization in problem solving.   Psychological Monographs, 54 (6) (Whole No. 248).

Mandler J. M. , & Mandler G. ( 1964 ). Thinking from associationism to Gestalt. New York : Wiley.

Markman A. B. , & Medin D. L. ( 2002 ). Decision making. In D. Medin (Ed.), Stevens’ handbook of experimental psychology, Vol. 2. Memory and cognitive processes (2nd ed., pp. 413–466). New York : Wiley.

Mayer R. E. ( 1992 ). Thinking, problem solving, cognition (2nd ed). New York : Freeman.

Mayer R. E. ( 1995 ). The search for insight: Grappling with Gestalt psychology’s unanswered questions. In R. J. Sternberg & J. E. Davidson (Eds.), The nature of insight (pp. 3–32). Cambridge, MA : MIT Press.

Mayer R. E. ( 2008 ). Learning and instruction. Upper Saddle River, NJ : Merrill Prentice Hall.

Mayer R. E. ( 2009 ). Information processing. In T. L. Good (Ed.), 21st century education: A reference handbook (pp. 168–174). Thousand Oaks, CA : Sage.

Mayer R. E. , & Wittrock M. C. ( 2006 ). Problem solving. In P. A. Alexander & P. H. Winne (Eds.), Handbook of educational psychology (2nd ed., pp. 287–304). Mahwah, NJ : Erlbaum.

McCloskey M. ( 1983 ). Intuitive physics.   Scientific American, 248 (4), 122–130.

Metcalfe J. , & Wiebe D. ( 1987 ). Intuition in insight and non-insight problem solving. Memory and Cognition, 15, 238–246.

Newell A. , & Simon H. A. ( 1972 ). Human problem solving. Englewood Cliffs, NJ : Prentice-Hall.

Nickerson R. S. ( 1999 ). Enhancing creativity. In R. J. Sternberg (Ed.), Handbook of creativity (pp. 392–430). New York : Cambridge University Press.

Nunes T. , Schliemann A. D. , & Carraher D. W , ( 1993 ). Street mathematics and school mathematics. Cambridge, England : Cambridge University Press.

Robbins P. , & Aydede M. (Eds.). ( 2009 ). The Cambridge handbook of situated cognition. New York : Cambridge University Press.

Rogers T. T. , & McClelland J. L. ( 2004 ). Semantic cognition: A parallel distributed processing approach. Cambridge, MA : MIT Press.

Singley M. K. , & Anderson J. R. ( 1989 ). The transfer of cognitive skill. Cambridge, MA : Harvard University Press.

Sternberg R. J. ( 1990 ). Metaphors of mind: Conceptions of the nature of intelligence. New York : Cambridge University Press.

Sternberg R. J. ( 1999 ). Handbook of creativity. New York : Cambridge University Press.

Sternberg R. J. , & Gregorenko E. L. (Eds.). ( 2003 ). The psychology of abilities, competencies, and expertise. New York : Cambridge University Press.

Tharp R. G. , & Gallimore R. ( 1988 ). Rousing minds to life: Teaching, learning, and schooling in social context. New York : Cambridge University Press.

Thorndike E. L. ( 1911 ). Animal intelligence. New York: Hafner.

Thorndike E. L. , & Woodworth R. S. ( 1901 ). The influence of improvement in one mental function upon the efficiency of other functions. Psychological Review, 8, 247–261.

Wertheimer M. ( 1959 ). Productive thinking. New York : Harper and Collins.

Wundt W. ( 1973 ). An introduction to experimental psychology. New York : Arno Press. (Original work published in 1911).

Further Reading

Baron, J. ( 2008 ). Thinking and deciding (4th ed). New York: Cambridge University Press.

Duncker, K. ( 1945 ). On problem solving. Psychological Monographs , 58(3) (Whole No. 270).

Holyoak, K. J. , & Morrison, R. G. ( 2005 ). The Cambridge handbook of thinking and reasoning . New York: Cambridge University Press.

Mayer, R. E. , & Wittrock, M. C. ( 2006 ). Problem solving. In P. A. Alexander & P. H. Winne (Eds.), Handbook of educational psychology (2nd ed., pp. 287–304). Mahwah, NJ: Erlbaum.

Sternberg, R. J. , & Ben-Zeev, T. ( 2001 ). Complex cognition: The psychology of human thought . New York: Oxford University Press.

Weisberg, R. W. ( 2006 ). Creativity . New York: Wiley.

• About Oxford Academic
• Publish journals with us
• University press partners
• What we publish
• New features  
• Open access
• Institutional account management
• Rights and permissions
• Get help with access
• Accessibility
• Advertising
• Media enquiries
• Oxford University Press
• Oxford Languages
• University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

• Copyright © 2024 Oxford University Press
• Cookie settings
• Cookie policy
• Privacy policy
• Legal notice

This Feature Is Available To Subscribers Only

Sign In or Create an Account

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

The Process of Problem Solving

• Editor's Choice
• Experimental Psychology
• Problem Solving

In a 2013 article published in the Journal of Cognitive Psychology , Ngar Yin Louis Lee (Chinese University of Hong Kong) and APS William James Fellow Philip N. Johnson-Laird (Princeton University) examined the ways people develop strategies to solve related problems. In a series of three experiments, the researchers asked participants to solve series of matchstick problems.

In matchstick problems, participants are presented with an array of joined squares. Each square in the array is comprised of separate pieces. Participants are asked to remove a certain number of pieces from the array while still maintaining a specific number of intact squares. Matchstick problems are considered to be fairly sophisticated, as there is generally more than one solution, several different tactics can be used to complete the task, and the types of tactics that are appropriate can change depending on the configuration of the array.

Louis Lee and Johnson-Laird began by examining what influences the tactics people use when they are first confronted with the matchstick problem. They found that initial problem-solving tactics were constrained by perceptual features of the array, with participants solving symmetrical problems and problems with salient solutions faster. Participants frequently used tactics that involved symmetry and salience even when other solutions that did not involve these features existed.

To examine how problem solving develops over time, the researchers had participants solve a series of matchstick problems while verbalizing their problem-solving thought process. The findings from this second experiment showed that people tend to go through two different stages when solving a series of problems.

People begin their problem-solving process in a generative manner during which they explore various tactics — some successful and some not. Then they use their experience to narrow down their choices of tactics, focusing on those that are the most successful. The point at which people begin to rely on this newfound tactical knowledge to create their strategic moves indicates a shift into a more evaluative stage of problem solving.

In the third and last experiment, participants completed a set of matchstick problems that could be solved using similar tactics and then solved several problems that required the use of novel tactics.  The researchers found that participants often had trouble leaving their set of successful tactics behind and shifting to new strategies.

From the three studies, the researchers concluded that when people tackle a problem, their initial moves may be constrained by perceptual components of the problem. As they try out different tactics, they hone in and settle on the ones that are most efficient; however, this deduced knowledge can in turn come to constrain players’ generation of moves — something that can make it difficult to switch to new tactics when required.

These findings help expand our understanding of the role of reasoning and deduction in problem solving and of the processes involved in the shift from less to more effective problem-solving strategies.

Reference Louis Lee, N. Y., Johnson-Laird, P. N. (2013). Strategic changes in problem solving. Journal of Cognitive Psychology, 25 , 165–173. doi: 10.1080/20445911.2012.719021

good work for other researcher

APS regularly opens certain online articles for discussion on our website. Effective February 2021, you must be a logged-in APS member to post comments. By posting a comment, you agree to our Community Guidelines and the display of your profile information, including your name and affiliation. Any opinions, findings, conclusions, or recommendations present in article comments are those of the writers and do not necessarily reflect the views of APS or the article’s author. For more information, please see our Community Guidelines .

Please login with your APS account to comment.

Careers Up Close: Joel Anderson on Gender and Sexual Prejudices, the Freedoms of Academic Research, and the Importance of Collaboration

Joel Anderson, a senior research fellow at both Australian Catholic University and La Trobe University, researches group processes, with a specific interest on prejudice, stigma, and stereotypes.

Experimental Methods Are Not Neutral Tools

Ana Sofia Morais and Ralph Hertwig explain how experimental psychologists have painted too negative a picture of human rationality, and how their pessimism is rooted in a seemingly mundane detail: methodological choices. 

APS Fellows Elected to SEP

In addition, an APS Rising Star receives the society’s Early Investigator Award.

Privacy Overview

Thinking and Intelligence

Solving Problems

Learning objectives.

• Describe problem solving strategies, including algorithms and heuristics

People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy for solving the problem.

Problem-Solving Strategies

When you are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution.

A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them. For example, a well-known strategy is trial and error . The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.

Another type of strategy is an algorithm. An algorithm is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?

A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):

• When one is faced with too much information
• When the time to make a decision is limited
• When the decision to be made is unimportant
• When there is access to very little information to use in making the decision
• When an appropriate heuristic happens to come to mind in the same moment

Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.

What problem-solving method could you use to solve Einstein’s famous riddle?

https://youtube.com/watch?v=1rDVz_Fb6HQ%3Flist%3DPLUmyCeox8XCwB8FrEfDQtQZmCc2qYMS5a

You can view the transcript for “Can you solve “Einstein’s Riddle”? – Dan Van der Vieren” here (opens in new window) .

Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.

Everyday Connections: Solving Puzzles

Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below (Figure 1) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.

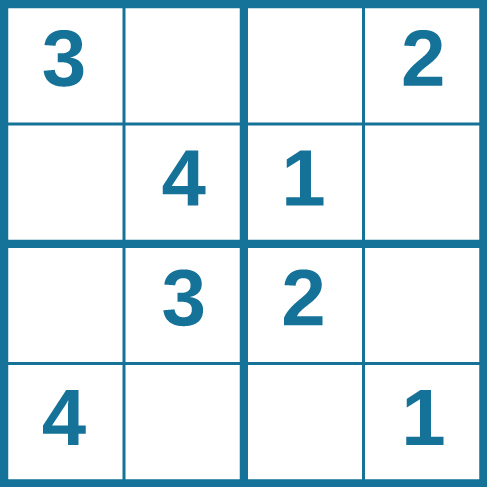
Here is another popular type of puzzle that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:

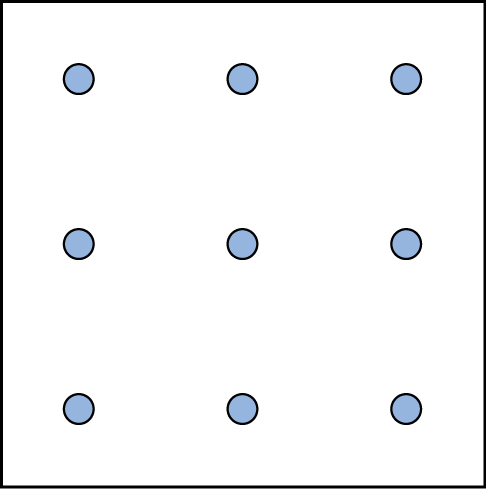
Take a look at the “Puzzling Scales” logic puzzle below (Figure 3). Sam Loyd, a well-known puzzle master, created and refined countless puzzles throughout his lifetime (Cyclopedia of Puzzles, n.d.).

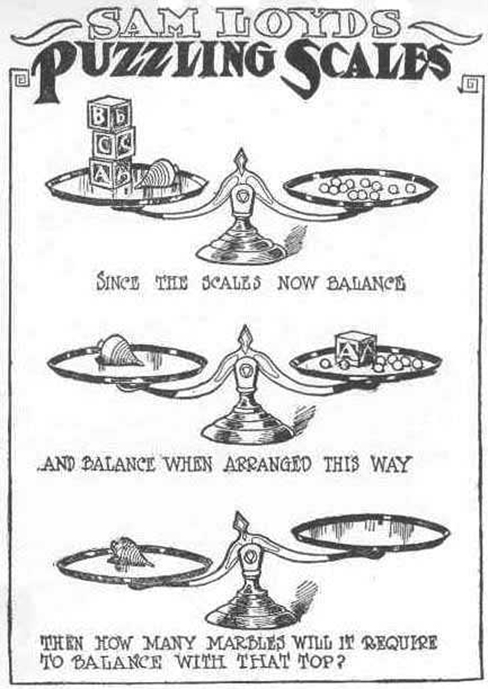
Were you able to determine how many marbles are needed to balance the scales in the Puzzling Scales? You need nine. Were you able to solve the other problems above? Here are the answers:

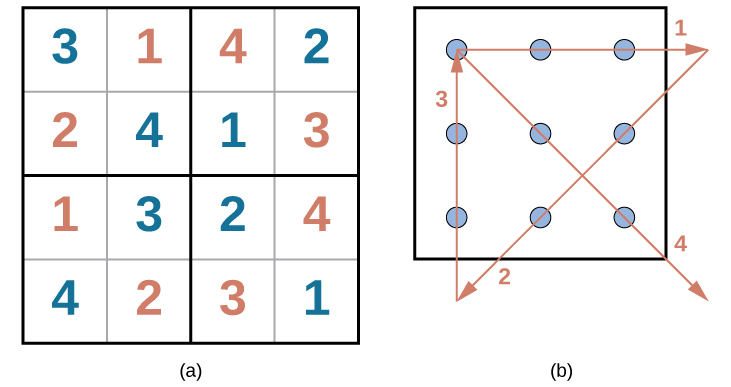
CC licensed content, Original

• Modification and adaptation. Provided by : Lumen Learning. License : CC BY: Attribution

CC licensed content, Shared previously

• Problem-Solving. Authored by : OpenStax College. Located at : https://openstax.org/books/psychology-2e/pages/7-3-problem-solving . License : CC BY: Attribution . License Terms : Download for free at https://openstax.org/books/psychology-2e/pages/1-introduction

All rights reserved content

• Can you solve Einsteinu2019s Riddle? . Authored by : Dan Van der Vieren. Provided by : Ted-Ed. Located at : https://www.youtube.com/watch?v=1rDVz_Fb6HQ&index=3&list=PLUmyCeox8XCwB8FrEfDQtQZmCc2qYMS5a . License : Other . License Terms : Standard YouTube License

method for solving problems

problem-solving strategy in which multiple solutions are attempted until the correct one is found

problem-solving strategy characterized by a specific set of instructions

mental shortcut that saves time when solving a problem

heuristic in which you begin to solve a problem by focusing on the end result

General Psychology Copyright © by OpenStax and Lumen Learning is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Facilitating Complex Thinking

Problem-Solving

Somewhat less open-ended than creative thinking is  problem-solving , the analysis and solution of tasks or situations that are complex or ambiguous and that pose difficulties or obstacles of some kind (Mayer & Wittrock, 2006). Problem-solving is needed, for example, when a physician analyzes a chest X-ray: a photograph of the chest is far from clear and requires skill, experience, and resourcefulness to decide which foggy-looking blobs to ignore, and which to interpret as real physical structures (and therefore real medical concerns). Problem-solving is also needed when a grocery store manager has to decide how to improve the sales of a product: should she put it on sale at a lower price, or increase publicity for it, or both? Will these actions actually increase sales enough to pay for their costs?

PROBLEM-SOLVING IN THE CLASSROOM

Problem-solving happens in classrooms when teachers present tasks or challenges that are deliberately complex and for which finding a solution is not straightforward or obvious. The responses of students to such problems, as well as the strategies for assisting them, show the key features of problem-solving. Consider this example and students’ responses to it. We have numbered and named the paragraphs to make it easier to comment about them individually:

Scene #1: A problem to be solved

A teacher gave these instructions: “Can you connect all of the dots below using only  four  straight lines?” She drew the following display on the chalkboard:

The problem itself and the procedure for solving it seemed very clear: simply experiment with different arrangements of four lines. But two volunteers tried doing it at the board, but were unsuccessful. Several others worked at it at their seats, but also without success.

Scene #2: Coaxing students to re-frame the problem

When no one seemed to be getting it, the teacher asked, “Think about how you’ve set up the problem in your mind—about what you believe the problem is about. For instance, have you made any assumptions about how long the lines ought to be? Don’t stay stuck on one approach if it’s not working!”

Scene #3: Alicia abandons a fixed response

After the teacher said this, Alicia indeed continued to think about how she saw the problem. “The lines need to be no longer than the distance across the square,” she said to herself. So she tried several more solutions, but none of them worked either.

The teacher walked by Alicia’s desk and saw what Alicia was doing. She repeated her earlier comment: “Have you assumed anything about how long the lines ought to be?”

Alicia stared at the teacher blankly, but then smiled and said, “Hmm! You didn’t actually  say  that the lines could be no longer than the matrix! Why not make them longer?” So she experimented again using oversized lines and soon discovered a solution:

Scene #4: Willem’s and Rachel’s alternative strategies

Meanwhile, Willem worked on the problem. As it happened, Willem loved puzzles of all kinds and had ample experience with them. He had not, however, seen this particular problem. “It  must  be a trick,” he said to himself because he knew from experience that problems posed in this way often were not what they first appeared to be. He mused to himself: “Think outside the box, they always tell you. . .” And  that  was just the hint he needed: he drew lines outside the box by making them longer than the matrix and soon came up with this solution:

When Rachel went to work, she took one look at the problem and knew the answer immediately: she had seen this problem before, though she could not remember where. She had also seen other drawing-related puzzles and knew that their solution always depended on making the lines longer, shorter, or differently angled than first expected. After staring at the dots briefly, she drew a solution faster than Alicia or even Willem. Her solution looked exactly like Willem’s.

This story illustrates two common features of problem-solving: the effect of degree of structure or constraint on problem-solving, and the effect of mental obstacles to solving problems. The next sections discuss each of these features and then look at common techniques for solving problems.

The Effect of Constraints: Well-Structured Versus Ill-Structured Problems

Problems vary in how much information they provide for solving a problem, as well as in how many rules or procedures are needed for a solution. A  well-structured problem  provides much of the information needed and can in principle be solved using relatively few clearly understood rules. Classic examples are the word problems often taught in math lessons or classes: everything you need to know is contained within the stated problem and the solution procedures are relatively clear and precise. An  ill-structured problem  has the converse qualities: the information is not necessarily within the problem, solution procedures are potentially quite numerous, and multiple solutions are likely (Voss, 2006). Extreme examples are problems like “How can the world achieve lasting peace?” or “How can teachers ensure that students learn?”

By these definitions, the nine-dot problem is relatively well-structured—though not completely. Most of the information needed for a solution is provided in Scene #1: there are nine dots shown and instructions given to draw four lines. But not  all  necessary information was given: students needed to consider lines that were longer than implied in the original statement of the problem. Students had to “think outside the box,” as Willem said—in this case, literally.

When a problem is well-structured, so are its solution procedures likely to be as well. A well-defined procedure for solving a particular kind of problem is often called an  algorithm ; examples are the procedures for multiplying or dividing two numbers or the instructions for using a computer (Leiserson, et al., 2001). Algorithms are only effective when a problem is very well-structured and there is no question about whether the algorithm is an appropriate choice for the problem. In that situation, it pretty much guarantees a correct solution. They do not work well, however, with ill-structured problems, where they are ambiguities and questions about how to proceed or even about precisely  what  the problem is about. In those cases, it is more effective to use  heuristics , which are general strategies—“rules of thumb,” so to speak—that do not always work but often do, or that provide at least partial solutions. When beginning research for a term paper, for example, a useful heuristic is to scan the library catalog for titles that look relevant. There is no guarantee that this strategy will yield the books most needed for the paper, but the strategy works enough of the time to make it worth trying.

In the nine-dot problem, most students began in Scene #1 with a simple algorithm that can be stated like this: “Draw one line, then draw another, and another, and another.” Unfortunately, this simple procedure did not produce a solution, so they had to find other strategies for a solution. Three alternatives are described in Scenes #3 (for Alicia) and 4 (for Willem and Rachel). Of these, Willem’s response resembled a heuristic the most: he knew from experience that a good  general  strategy that  often  worked for such problems was to suspect deception or trick in how the problem was originally stated. So he set out to question what the teacher had meant by the word  line  and came up with an acceptable solution as a result.

Common Obstacles to Solving Problems

The example also illustrates two common problems that sometimes happen during problem-solving. One of these is  functional fixedness : a tendency to regard the  functions  of objects and ideas as  fixed  (German & Barrett, 2005). Over time, we get so used to one particular purpose for an object that we overlook other uses. We may think of a dictionary, for example, as necessarily something to verify spellings and definitions, but it also can function as a gift, a doorstop, or a footstool. For students working on the nine-dot matrix described in the last section, the notion of “drawing” a line was also initially fixed; they assumed it to be connecting dots but not extending lines beyond the dots. Functional fixedness sometimes is also called  response set , the tendency for a person to frame or think about each problem in a series in the same way as the previous problem, even when doing so is not appropriate for later problems. In the example of the nine-dot matrix described above, students often tried one solution after another, but each solution was constrained by a set response not  to extend any line beyond the matrix.

Functional fixedness and the response set are obstacles in  problem representation , the way that a person understands and organizes information provided in a problem. If information is misunderstood or used inappropriately, then mistakes are likely—if indeed the problem can be solved at all. With the nine-dot matrix problem, for example, construing the instruction to draw four lines as meaning “draw four lines entirely within the matrix” means that the problem simply could not be solved. For another, consider this problem: “The number of water lilies on a lake doubles each day. Each water lily covers exactly one square foot. If it takes 100 days for the lilies to cover the lake exactly, how many days does it take for the lilies to cover exactly half of the lake?” If you think that the size of the lilies affects the solution to this problem, you have not represented the problem correctly. Information about lily size is  not  relevant to the solution and only serves to distract from the truly crucial information, the fact that the lilies  double  their coverage each day. (The answer, incidentally, is that the lake is half covered in 99 days; can you think why?)

Strategies to Assist Problem-Solving

Just as there are cognitive obstacles to problem-solving, there are also general strategies that help the process be successful, regardless of the specific content of a problem (Thagard, 2005). One helpful strategy is  problem analysis —identifying the parts of the problem and working on each part separately. Analysis is especially useful when a problem is ill-structured. Consider this problem, for example: “Devise a plan to improve bicycle transportation in the city.” Solving this problem is easier if you identify its parts or component subproblems, such as (1) installing bicycle lanes on busy streets, (2) educating cyclists and motorists to ride safely, (3) fixing potholes on streets used by cyclists, and (4) revising traffic laws that interfere with cycling. Each separate subproblem is more manageable than the original, general problem. The solution of each subproblem contributes to the solution of the whole, though of course is not equivalent to a whole solution.

Another helpful strategy is  working backward   from  a final solution to the originally stated problem. This approach is especially helpful when a problem is well-structured but also has elements that are distracting or misleading when approached in a forward, normal direction. The water lily problem described above is a good example: starting with the day when  all  the lake is covered (Day 100), ask what day would it, therefore, be half-covered (by the terms of the problem, it would have to be the day before, or Day 99). Working backward, in this case, encourages reframing the extra information in the problem (i. e. the size of each water lily) as merely distracting, not as crucial to a solution.

A third helpful strategy is  analogical thinking —using knowledge or experiences with similar features or structures to help solve the problem at hand (Bassok, 2003). In devising a plan to improve bicycling in the city, for example, an analogy of cars with bicycles is helpful in thinking of solutions: improving conditions for both vehicles requires many of the same measures (improving the roadways, educating drivers). Even solving simpler, more basic problems is helped by considering analogies. A first-grade student can partially decode unfamiliar printed words by analogy to words he or she has learned already. If the child cannot yet read the word screen , for example, he can note that part of this word looks similar to words he may already know, such as  seen  or  green,  and from this observation derive a clue about how to read the word  screen . Teachers can assist this process, as you might expect, by suggesting reasonable, helpful analogies for students to consider.

Video 5.4.1. Problem Solving explains strategies used for solving problems.

Many systems for problem-solving can be taught to learners (Pressley, 1995). There are problem-solving strategies to improve general problem solving (Burkell, Schneider, & Pressley, 1990; Mayer, 1987; Sternberg, 1988), scientific thinking (Kuhn, 1989), mathematical problem solving (Schoenfeld, 1989), and writing during the elementary years (Harris & Graham, 1992a) and during adolescence (Applebee, 1984; Langer & Applebee, 1987).

A problem-solving system that can be used in a variety of curriculum areas and with a variety of problems is called IDEAL (Bransford & Steen, 1984). IDEAL involves five stages of problem-solving:

• Identify the problem. Learners must know what the problem is before they can solve it. During this stage of problem-solving, learners ask themselves whether they understand what the problem is and whether they have stated it clearly.
• Define terms. During this stage, learners check whether they understand what each word in the problem statement means.
• Explore strategies. At this stage, learners compile relevant information and try out strategies to solve the problem. This can involve drawing diagrams, working backward to solve a mathematical or reading comprehension problem, or breaking complex problems into manageable units.
• Act on the strategy. Once learners have explored a variety of strategies, they select one and now use it.
• Look at the effects. During the final stage of the IDEAL method, learners ask themselves whether they have come up with an acceptable solution.

Video 5.4.2. The Problem Solving Model explains the process involved in solving problems. These steps can be explicitly taught to enhance problem-solving skills.

Candela Citations

• Problem-Solving. Authored by : Nicole Arduini-Van Hoose. Provided by : Hudson Valley Community College. Retrieved from : https://courses.lumenlearning.com/edpsy/chapter/problemsolving. License : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike
• Educational Psychology. Authored by : Kelvin Seifert and Rosemary Sutton. Provided by : The Saylor Foundation. Retrieved from : https://courses.lumenlearning.com/educationalpsychology. License : CC BY: Attribution
• Educational Psychology. Authored by : Bohlin. License : CC BY: Attribution
• Problem Solving. Authored by : Carole Yue. Provided by : Khan Academy. Retrieved from : https://youtu.be/J3GGx9wy07w. License : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike
• The Problem Solving Model. Provided by : Gregg Learning. Retrieved from : https://youtu.be/CDk_BD1LXiI. License : All Rights Reserved

Educational Psychology Copyright © 2020 by Nicole Arduini-Van Hoose is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Best Family Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

Problem-Solving Strategies and Obstacles

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Sean is a fact-checker and researcher with experience in sociology, field research, and data analytics.

JGI / Jamie Grill / Getty Images

• Application
• Improvement

From deciding what to eat for dinner to considering whether it's the right time to buy a house, problem-solving is a large part of our daily lives. Learn some of the problem-solving strategies that exist and how to use them in real life, along with ways to overcome obstacles that are making it harder to resolve the issues you face.

What Is Problem-Solving?

In cognitive psychology , the term 'problem-solving' refers to the mental process that people go through to discover, analyze, and solve problems.

A problem exists when there is a goal that we want to achieve but the process by which we will achieve it is not obvious to us. Put another way, there is something that we want to occur in our life, yet we are not immediately certain how to make it happen.

Maybe you want a better relationship with your spouse or another family member but you're not sure how to improve it. Or you want to start a business but are unsure what steps to take. Problem-solving helps you figure out how to achieve these desires.

The problem-solving process involves:

• Discovery of the problem
• Deciding to tackle the issue
• Seeking to understand the problem more fully
• Researching available options or solutions
• Taking action to resolve the issue

Before problem-solving can occur, it is important to first understand the exact nature of the problem itself. If your understanding of the issue is faulty, your attempts to resolve it will also be incorrect or flawed.

Problem-Solving Mental Processes

Several mental processes are at work during problem-solving. Among them are:

• Perceptually recognizing the problem
• Representing the problem in memory
• Considering relevant information that applies to the problem
• Identifying different aspects of the problem
• Labeling and describing the problem

Problem-Solving Strategies

There are many ways to go about solving a problem. Some of these strategies might be used on their own, or you may decide to employ multiple approaches when working to figure out and fix a problem.

An algorithm is a step-by-step procedure that, by following certain "rules" produces a solution. Algorithms are commonly used in mathematics to solve division or multiplication problems. But they can be used in other fields as well.

In psychology, algorithms can be used to help identify individuals with a greater risk of mental health issues. For instance, research suggests that certain algorithms might help us recognize children with an elevated risk of suicide or self-harm.

One benefit of algorithms is that they guarantee an accurate answer. However, they aren't always the best approach to problem-solving, in part because detecting patterns can be incredibly time-consuming.

There are also concerns when machine learning is involved—also known as artificial intelligence (AI)—such as whether they can accurately predict human behaviors.

Heuristics are shortcut strategies that people can use to solve a problem at hand. These "rule of thumb" approaches allow you to simplify complex problems, reducing the total number of possible solutions to a more manageable set.

If you find yourself sitting in a traffic jam, for example, you may quickly consider other routes, taking one to get moving once again. When shopping for a new car, you might think back to a prior experience when negotiating got you a lower price, then employ the same tactics.

While heuristics may be helpful when facing smaller issues, major decisions shouldn't necessarily be made using a shortcut approach. Heuristics also don't guarantee an effective solution, such as when trying to drive around a traffic jam only to find yourself on an equally crowded route.

Trial and Error

A trial-and-error approach to problem-solving involves trying a number of potential solutions to a particular issue, then ruling out those that do not work. If you're not sure whether to buy a shirt in blue or green, for instance, you may try on each before deciding which one to purchase.

This can be a good strategy to use if you have a limited number of solutions available. But if there are many different choices available, narrowing down the possible options using another problem-solving technique can be helpful before attempting trial and error.

In some cases, the solution to a problem can appear as a sudden insight. You are facing an issue in a relationship or your career when, out of nowhere, the solution appears in your mind and you know exactly what to do.

Insight can occur when the problem in front of you is similar to an issue that you've dealt with in the past. Although, you may not recognize what is occurring since the underlying mental processes that lead to insight often happen outside of conscious awareness .

Research indicates that insight is most likely to occur during times when you are alone—such as when going on a walk by yourself, when you're in the shower, or when lying in bed after waking up.

How to Apply Problem-Solving Strategies in Real Life

If you're facing a problem, you can implement one or more of these strategies to find a potential solution. Here's how to use them in real life:

• Create a flow chart . If you have time, you can take advantage of the algorithm approach to problem-solving by sitting down and making a flow chart of each potential solution, its consequences, and what happens next.
• Recall your past experiences . When a problem needs to be solved fairly quickly, heuristics may be a better approach. Think back to when you faced a similar issue, then use your knowledge and experience to choose the best option possible.
• Start trying potential solutions . If your options are limited, start trying them one by one to see which solution is best for achieving your desired goal. If a particular solution doesn't work, move on to the next.
• Take some time alone . Since insight is often achieved when you're alone, carve out time to be by yourself for a while. The answer to your problem may come to you, seemingly out of the blue, if you spend some time away from others.

Obstacles to Problem-Solving

Problem-solving is not a flawless process as there are a number of obstacles that can interfere with our ability to solve a problem quickly and efficiently. These obstacles include:

• Assumptions: When dealing with a problem, people can make assumptions about the constraints and obstacles that prevent certain solutions. Thus, they may not even try some potential options.
• Functional fixedness : This term refers to the tendency to view problems only in their customary manner. Functional fixedness prevents people from fully seeing all of the different options that might be available to find a solution.
• Irrelevant or misleading information: When trying to solve a problem, it's important to distinguish between information that is relevant to the issue and irrelevant data that can lead to faulty solutions. The more complex the problem, the easier it is to focus on misleading or irrelevant information.
• Mental set: A mental set is a tendency to only use solutions that have worked in the past rather than looking for alternative ideas. A mental set can work as a heuristic, making it a useful problem-solving tool. However, mental sets can also lead to inflexibility, making it more difficult to find effective solutions.

How to Improve Your Problem-Solving Skills

In the end, if your goal is to become a better problem-solver, it's helpful to remember that this is a process. Thus, if you want to improve your problem-solving skills, following these steps can help lead you to your solution:

• Recognize that a problem exists . If you are facing a problem, there are generally signs. For instance, if you have a mental illness , you may experience excessive fear or sadness, mood changes, and changes in sleeping or eating habits. Recognizing these signs can help you realize that an issue exists.
• Decide to solve the problem . Make a conscious decision to solve the issue at hand. Commit to yourself that you will go through the steps necessary to find a solution.
• Seek to fully understand the issue . Analyze the problem you face, looking at it from all sides. If your problem is relationship-related, for instance, ask yourself how the other person may be interpreting the issue. You might also consider how your actions might be contributing to the situation.
• Research potential options . Using the problem-solving strategies mentioned, research potential solutions. Make a list of options, then consider each one individually. What are some pros and cons of taking the available routes? What would you need to do to make them happen?
• Take action . Select the best solution possible and take action. Action is one of the steps required for change . So, go through the motions needed to resolve the issue.
• Try another option, if needed . If the solution you chose didn't work, don't give up. Either go through the problem-solving process again or simply try another option.

You can find a way to solve your problems as long as you keep working toward this goal—even if the best solution is simply to let go because no other good solution exists.

Sarathy V. Real world problem-solving .  Front Hum Neurosci . 2018;12:261. doi:10.3389/fnhum.2018.00261

Dunbar K. Problem solving . A Companion to Cognitive Science . 2017. doi:10.1002/9781405164535.ch20

Stewart SL, Celebre A, Hirdes JP, Poss JW. Risk of suicide and self-harm in kids: The development of an algorithm to identify high-risk individuals within the children's mental health system . Child Psychiat Human Develop . 2020;51:913-924. doi:10.1007/s10578-020-00968-9

Rosenbusch H, Soldner F, Evans AM, Zeelenberg M. Supervised machine learning methods in psychology: A practical introduction with annotated R code . Soc Personal Psychol Compass . 2021;15(2):e12579. doi:10.1111/spc3.12579

Mishra S. Decision-making under risk: Integrating perspectives from biology, economics, and psychology . Personal Soc Psychol Rev . 2014;18(3):280-307. doi:10.1177/1088868314530517

Csikszentmihalyi M, Sawyer K. Creative insight: The social dimension of a solitary moment . In: The Systems Model of Creativity . 2015:73-98. doi:10.1007/978-94-017-9085-7_7

Chrysikou EG, Motyka K, Nigro C, Yang SI, Thompson-Schill SL. Functional fixedness in creative thinking tasks depends on stimulus modality .  Psychol Aesthet Creat Arts . 2016;10(4):425‐435. doi:10.1037/aca0000050

Huang F, Tang S, Hu Z. Unconditional perseveration of the short-term mental set in chunk decomposition .  Front Psychol . 2018;9:2568. doi:10.3389/fpsyg.2018.02568

National Alliance on Mental Illness. Warning signs and symptoms .

Mayer RE. Thinking, problem solving, cognition, 2nd ed .

Schooler JW, Ohlsson S, Brooks K. Thoughts beyond words: When language overshadows insight. J Experiment Psychol: General . 1993;122:166-183. doi:10.1037/0096-3445.2.166

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Insight Learning (Definition+ 4 Stages + Examples)

Have you ever been so focused on a problem that it took stepping away for you to figure it out? You can’t find the solution when you’re looking at all of the moving parts, but once you get distracted with something else - “A-ha!” you have it. 

When a problem cannot be solved by applying an obvious step-by-step solving sequence,   Insight learning occurs when the mind rearranges the elements of the problem and finds connections that were not obvious in the initial presentation of the problem. People experience this as a sudden A-ha moment.

Humans aren’t the only species that have these “A-ha” moments. Work with other species helped psychologists understand the definition and stages of Insight Learning. This video is going to break down those stages and how you can help to move these “a-ha” moments along. 

What Is Insight Learning? 

Insight learning is a process that leads to a sudden realization regarding a problem. Often, the learner has tried to understand the problem, but steps away before the change in perception occurs. Insight learning is often compared to trial-and-error learning, but it’s slightly different.

Rather than just trying different random solutions, insight learning requires more comprehension. Learners aim to understand the relationships between the pieces of the puzzle. They use patterns, organization, and past knowledge to solve the problem at hand. 

Is Insight Learning Only Observed In Humans? 

Humans aren’t the only species that learn with insight. Not all species use this process - just the ones that are closest to us intellectually. Insight learning was first discovered not by observing humans, but by observing chimps. 

In the early 1900s, Wolfgang Köhler observed chimpanzees as they solved problems. Köhler’s most famous subject was a chimp named Sultan. The psychologist gave Sultan two sticks of different sizes and placed a banana outside of Sultan’s cage. He watched as Sultan looked at the sticks and tried to reach for the banana with no success. Eventually, Sultan gave up and got distracted. But it was during this time that Köhler noticed Sultan having an “epiphany.” The chimp went back to the sticks, placed one inside of the other, and used this to bring the banana to him. 

Since Köhler’s original observations took place, psychologists looked deeper into the insight process and when you are more likely to experience that “a-ha” moment. There isn’t an exact science to insight learning, but certain theories suggest that some places are better for epiphanies than others. 

Four Stages of Insight Learning 

But how does insight learning happen? Multiple models have been developed, but the four-stage model is the most popular. The four stages of insight learning are preparation, incubation, insight, and verification. 

Preparation

The process begins as you try to solve the problem. You have the materials and information in front of you and begin to make connections. Although you see the relationships between the materials, things just haven’t “clicked” yet. This is the stage where you start to get frustrated. 

During the incubation period, you “give up” for a short period of time. Although you’ve abandoned the project, your brain is still making connections on an unconscious level. 

When the right connections have been made in your mind, the “a-ha” moment occurs. Eureka! You have an epiphany! 

Verification

Now, you just have to make sure that your epiphany is right. You test out your solution and hopefully, it works! This is a great moment in your learning journey. The connections you make solving this problem are likely to help you in the future. 

Examples of Insight Learning

Insight learning refers to the sudden realization or understanding of a solution to a problem without the need for trial-and-error attempts. It's like a "light bulb" moment when things suddenly make sense. Here are some examples of insight learning:

• The Matchstick Problem : Realizing you can light a match and use it to illuminate a dark room instead of fumbling around in the dark.
• Sudoku Puzzles : Suddenly seeing a pattern or number placement that you hadn't noticed before, allowing you to complete the puzzle.
• The Two Rope Problem : In an experiment, a person is given two ropes hanging from the ceiling and is asked to tie them together. The solution involves swinging one rope like a pendulum and grabbing it with the other.
• Opening Jars : After struggling to open a jar, you remember you can tap its lid lightly or use a rubber grip to make it easier.
• Tangram Puzzles : Suddenly realizing how to arrange the geometric pieces to complete the picture without any gaps.
• Escape Rooms : Having an "aha" moment about a clue that helps you solve a puzzle and move to the next challenge.
• The Nine Dot Problem : Connecting all nine dots using only four straight lines without lifting the pen.
• Cooking : Realizing you can soften butter quickly by grating it or placing it between two sheets of parchment paper and rolling it.
• Math Problems : Suddenly understanding a complex math concept or solution method after pondering it for a while.
• Guitar Tuning : Realizing you can use the fifth fret of one string to tune the next string.
• Traffic Routes : Discovering a faster or more efficient route to your destination without using a GPS.
• Packing Suitcases : Figuring out how to fit everything by rolling clothes or rearranging items in a specific order.
• The Crow and the Pitcher : A famous Aesop's fable where a thirsty crow drops pebbles into a pitcher to raise the water level and drink.
• Computer Shortcuts : Discovering a keyboard shortcut that makes a task you frequently do much quicker.
• Gardening : Realizing you can use eggshells or coffee grounds as a natural fertilizer.
• Physics Problems : After struggling with a concept, suddenly understanding the relationship between two variables in an equation.
• Art : Discovering a new technique or perspective that transforms your artwork.
• Sports : Realizing a different way to grip a tennis racket or baseball bat that improves your game.
• Language Learning : Suddenly understanding the grammar or pronunciation rule that was previously confusing.
• DIY Projects : Figuring out a way to repurpose old items in your home, like using an old ladder as a bookshelf.

Where Is the Best Place to Have an Epiphany? 

But what if you want to have an epiphany? You’re stuck on a problem and you can’t take it anymore. You want to abandon it, but you’re not sure what you should do for this epiphany to take place. Although an “a-ha” moment isn’t guaranteed, studies suggest that the following activities or places can help you solve a tough problem. 

The Three B’s of Creativity 

Creativity and divergent thinking are key to solving problems. And some places encourage creativity more than others. Researchers believe that you can kickstart divergent thinking with the three B’s: bed, bath, and the bus. 

Sleep 

“Bed” might be your best bet out of the three. Studies show that if you get a full night’s sleep, you will be twice as likely to solve a problem than if you stay up all night. This could be due to the REM sleep that you get throughout the night. During REM sleep , your brain is hard at work processing the day’s information and securing connections. Who knows - maybe you’ll dream up the answer to your problems tonight!

Meditation 

The word for “insight” in the Pali language is vipassana. If you have ever been interested in meditation , you might have seen this word before. You can do a vipassana meditation at home, or you can go to a 10-day retreat. These retreats are often silent and are set up to cultivate mind-body awareness. 

You certainly don’t have to sign up for a 10-day silent retreat to solve a problem that is bugging you. (Although, you may have a series of breakthroughs!) Try meditating for 20 minutes at a time. Studies show that this can increase the likelihood of solving a problem. 

Laugh! 

How do you feel when you have an epiphany? Good, right? The next time you’re trying to solve a problem, check in with your emotions. You are more likely to experience insight when you’re in a positive mood. Positivity opens your mind and gives your mind more freedom to explore. That exploration may just lead you to your solution. 

Be patient when you’re trying to solve problems. Take breaks when you need to and make sure that you are taking care of yourself. This approach will help you solve problems faster and more efficiently!

Insight Vs. Other Types Of Learning.

Learning by insight is  not  learning by trial and  error, nor by observation  and imitation. Learning by insight is a learning theory accepted by the Gestalt  school of psychology, which disagrees with the behaviorist  school, which claims that all learning occurs through conditioning from the  external environment.

Gestalt is a German word that approximately translates as ‘an organized whole  that has properties  and elements in addition to the sum of its parts .’ By viewing a problem as a ‘gestalt’ , the learner does not simply react to whatever she observes at the moment. She also imagines elements that could be present but are not and uses her imagination to combine parts of the problem that are presently not so combined in fact.  

Insight Vs. Trial And Error Learning

Imagine yourself in a maze-running competition. You and your rivals each have 10 goes. The first one to run the maze successfully wins $500. You may adopt a trial-and-error strategy, making random turning decisions and remembering whether those particular turns were successful or not for your next try. If you have a good memory and with a bit of luck, you will get to the exit and win the prize.

Completing the maze through trial and error requires no insight. If you had to run a different maze, you would have no advantage over running previous mazes with different designs. You have now learned to run this particular maze as predicted by behaviorist psychologists. External factors condition your maze running behavior. The cash prize motivates  you to run the maze in the first place. All maze dead ends act as punishments , which you remember not to repeat. All correct turns act as rewards , which you remember to repeat.

If you viewed the maze running competition as a gestalt, you might notice that it doesn't explicitly state in the competition rules that you must run along the designated paths to reach the exit.

Suppose you further noticed that the maze walls were made from cardboard. In that case, you may combine those 2 observations in your imagination and realize that you could just punch big holes in the walls or tear them down completely, to see around corners and directly run to the now visible exit.

Insight Vs. Learning Through Observation, Imitation, And Repetition

Observation, imitation, and repetition are at the heart of training. The violin teacher shows you how to hold your bow correctly; you practice your scales countless times before learning to play a sonata from Beethoven flawlessly. Mastering a sport or a musical instrument rarely comes from a flash of insight but a lot of repetition and error correction from your teacher.

Herbert Lawford, the Scottish tennis player, and 1887 Wimbledon champion, is credited for being the first player to play a topspin. Who could have taught it to him? Who could he have imitated? One can only speculate since no player at that time was being coached on how to hit topspin.

He could have only learned to play a topspin by having a novel insight. One possibility is that he played one by accident during training, by mistakenly hitting the ball at a flatter angle than normal. He could then have observed that his opponent was disorientated by the flatter and quicker bounce of the ball and realized the benefit of his ‘mistake’ .

Behaviorist theories of learning can probably explain how most successful and good tennis players are produced, but you need a Gestalt insight learning theory to explain Herbert Lawford.

Another interesting famous anecdote illustrating insight learning concerned Carl Friedrich Gauss when he was a 7-year-old pupil at school. His mathematics teacher seems to have adopted strict behaviorism in his teaching since the original story implies that he beat students with a switch.

One day the teacher set classwork requiring the students to add up all the numbers from 1 to 100. He expected his pupils to perform this calculation in how they were trained. He expected it to be a laborious and time-consuming task, giving him a long break. In just a few moments, young Gauss handed in the correct answer after having to make at most 2 calculations, which are easy to do in your head. How did he do it? Gauss saw the arithmetic sequence as a gestalt instead of adding all the numbers one at a time: 1+2+3+4…. +99+100 as he expected.

He realized that by breaking this sequence in half at 50, then snaking the last number (100) under the first number (1), and then adding the 2 halves of the arithmetic sequence like so:  

    1         +        2       +        3      +       4      +       5         +    ………….      +        48        +        49             +       50

100        +       99       +      98      +     97      +      96       +    …………...    +        53        +         52           +       51

101        +      101      +    101     +    101      +     101     +   …………….     +     101        +       101           +     101    

Arranged in this way, each number column adds up to 101, so all Gauss needed to do was calculate 50 x 101 = 5050.

Can Major Scientific Breakthroughs be made through observation and experiment alone?

Science is unapologetically an evidence-based inquiry. Observations, repeatable experiments, and hard, measurable data must support theories and explanations.

Since countless things can be observed and comparisons made, they cannot be done randomly for observations and experiments to advance knowledge. They must be guided by a good question and a  testable hypothesis. Before performing actual experiments and observations, scientists often first perform thought experiments . They think of ideal situations by imagining ways things could be or imaging away things that are.

Atoms were talked about long before electron microscopes could observe them. How could atoms be seriously discussed in ancient Greece long before the discoveries of modern chemistry? Pre-Socratic philosophers were puzzled by a purely philosophical problem, which they termed the problem of the one and many .  

People long observed that the world was made of many different things that didn't remain static but continuously changed into other various things. For example, a seed different from a tree changed into a tree over time. Small infants change into adults yet remain the same person. Boiling water became steam, and frozen water became ice.

Observing all of this in the world, philosophers didn’t simply take it for granted and aimed to profit from it practically through stimulus-response and trial and error learning. They were puzzled by how the world fit together as a whole.

To make sense of all this observable changing multiplicity, one needed to imagine an unobservable sameness behind it all. Yet, there is no obvious or immediate punishment or reward. Therefore, there seems to be no satisfying behaviorist reason behind philosophical speculations.

Thinkers such as Empedocles and Aristotle made associations between general properties in the world wetness, dryness, temperature, and phases of matter as follows:

• Earth :  dry, cold     
• Fire:  dry, hot
• Water:  wet, cold
• Air: hot or wet, depending on whether moisture or heat prevails in the atmosphere.

These 4 primitive elements transformed and combined give rise to the diversity we see in the world. However, this view was still too sensually based  to provide the world with sought-for coherence and unity. How could a multiplicity of truly basic stuff interact? Doesn't such an interaction presuppose something more fundamental in common?

The ratio of these 4 elements was thought to affect the properties of things. Stone contained more earth, while a rabbit had more water and fire, thus making it soft and giving it life. Although this theory correctly predicted that seemingly basic things like stones were complex compounds, it had some serious flaws.

For example, if you break a stone in half many times, the pieces never resemble fire, air, water, or earth.   

To account for how different things could be the same on one level and different on another level, Leucippus and his student Democritus reasoned that all things are the same in that they were made from some common primitive indivisible stuff but different due to the different ways or patterns in which this indivisible stuff or atoms could be arranged.

For atoms to be able to rearrange and recombine into different patterns led thinkers to the insight that if the atom idea was true, then logically, there had to be free spaces between the atoms for them to shift into. They had to imagine a vacuum, another phenomenon not directly observable since every nook and cranny in the world seems to be filled with some liquid, solid, or gas.  

This ancient notion of vacuum proved to be more than just a made-up story since it led to modern practical applications in the form of vacuum cleaners and food vacuum packing.

This insight that atoms and void exist makes no sense from a behaviorist learning standpoint. It cannot be explained in terms of stimulus-response or environmental conditioning and made no practical difference in the lives of ancient Greeks.  

For philosophers to feel compelled to hold onto notions, which at the time weren’t directly useful, it suggests that they must have felt some need to understand the universe as an intelligible ‘gestalt’ One may even argue that the word Cosmos, from the Greek word Kosmos, which roughly translates to ‘harmonious arrangement’ is at least a partial synonym.  

The Historical Development Of The Theory of Insight Learning

Wolfgang Kohler , the German gestalt psychologist, is credited for formulating the theory of insight learning, one of the first cognitive learning theories. He came up with the theory while first conducting experiments  in 1913 on 7 chimpanzees  on the island of Tenerife to observe how they learned to solve problems.

In one experiment, he dangled a banana from the top of a high cage. Boxes and poles were left in the cage with the chimpanzees. At first, the chimps used trial and error to get at the banana. They tried to jump up to the banana without success. After many failed attempts, Kohler noticed that they paused to think  for a while.  

After some time, they behaved more methodically by stacking the boxes on top of each other, making a raised platform from which they could swipe at the banana using the available poles. Kohler believed that chimps, like humans, were capable of experiencing flashes of insight, just like humans.

In another experiment, he placed a peanut down a long narrow tube attached to the cage's outer side. The chimpanzee tried scooping the peanut out with his hand and fingers, but to no avail, since the tube was too long and narrow. After sitting down to think, the chimp filled its mouth with water from a nearby water container in the cage and spat it into the tube.

The peanut floated up the tube within the chimp's reach. What is essential is that the chimp realized it could use water as a tool in a flash of insight, something it had never done before or never shown how  to do .  Kohler's conclusions contrasted with those of American psychologist Edward Thorndike , who, years back, conducted learning experiments on cats, dogs, and monkeys.

Through his experiments and research, Thorndike concluded that although there was a vast difference in learning speed and potential between monkey dogs and cats, he concluded that all animals, unlike humans, are not capable of genuine reasoned thought. According to him, Animals can only learn through stimulus-response conditioning, trial and error, and solve problems accidentally.

Kohler’s 4 Stage Model Of Insight Learning

From his observations of how chimpanzees solve complex problems, he concluded that the learning process went through the following 4 stages:

• Preparation:  Learners encounter the problem and begin to survey all relevant information and materials. They process stimuli and begin to make connections.
• Incubation: Learners get frustrated and may even seem to observers as giving up. However, their brains carry on processing information unconsciously.
• Insight: The learner finally achieves a breakthrough, otherwise called an epiphany or ‘Aha’ moment. This insight comes in a flash and is often a radical reorganization of the problem. It is a discontinuous leap in understanding rather than continuous with reasoning undertaken in the preparation phase.
• Verification: The learner now formally tests the new insight and sees if it works in multiple different situations. Mathematical insights are formally proved.

The 2 nd  and 3 rd  stages of insight learning are well described in anecdotes of famous scientific breakthroughs. In 1861, August Kekulé was contemplating the structure of the Benzene molecule. He knew it was a chain of 6 carbon atoms attached to 6 hydrogen atoms. Still, He got stuck   (incubation phase)  on working out how they could fit together to remain chemically stable.

He turned away from his desk and, facing the fireplace, fell asleep. He dreamt of a snake eating its tail and then spinning around. He woke up and realized (insight phase)  that these carbon-hydrogen chains can close onto themselves to form hexagonal rings. He then worked out the consequences of his new insight on Benzene rings. (Verification phase)

Suitably prepared minds can experience insights while observing ordinary day-to-day events. Many people must have seen apples fall from trees and thought nothing of it. When Newton saw an apple fall, he connected its fall to the action of the moon. If an unseen force pulls the apple from the tree top, couldn't the same force extends to the moon? This same force must be keeping the moon tethered in orbit around the earth, keeping it from whizzing off into space. Of course, this seems counterintuitive because if the moon is like the apple, should it not be crashing down to earth?

Newton's prepared mind understood the moon to be continuously falling to earth around the horizon's curve. Earth's gravitational pull on the moon balanced its horizontal velocity tangential to its orbit. If the apple were shot fast enough over the horizon from a cannon, it too, like the moon, would stay in orbit.

So, although before Newton, everyone was aware of gravity in a stimulus-response kind of way and even made practical use of it to weigh things, no one understood its universal implications.

Applying Insight Learning To The Classroom

The preparation-incubation-insight- verification cycle could be implemented by teachers in the classroom. Gestalt theory predicts that students learn best when they engage with the material; they are mentally prepared  for age, and maturity, having had experiences enabling them to relate to the material and having background knowledge that allows them to contextualize the material. When first presenting content they want to teach the students, teachers must make sure students are suitably prepared to receive the material, to successfully go through the preparation stage of learning.

Teachers should present the material holistically and contextually. For example, when teaching about the human heart, they should also teach where it is in the human body and its functional importance and relationship to other organs and parts of the body. Teachers could also connect other fields, such as comparing hearts to mechanical pumps.

Once the teacher has imparted sufficient background information to students, they should set a problem for their students to solve independently or in groups. The problem should require the students to apply what they have learned in a new way and make novel connections not explicitly made by the teacher during the lesson.

However, they must already know and be familiar with all the material they need to solve the problem. Students must be allowed to fumble their way to a solution  and make many mistakes , as this is vital for the incubation phase. The teacher should resist the temptation to spoon-feed them. Instead, teachers should use the Socratic method to coax the students into arriving at solutions and answers themselves.

Allowing the students to go through a sufficiently challenging incubation phase engages all their higher cognitive functions, such as logical and abstract reasoning, visualization, and imagination. It also habituates them to a bit of frustration to build the mental toughness to stay focused.

It also forces their brains to work hard in processing combining information to sufficiently own the insights they achieve, making it more likely that they will retain  the knowledge they gained and be able to apply it across different contexts.

Once students have written down their insights and solutions, the teacher should guide them through the verification phase. The teacher and students need to check and test the validity of the answers. Solutions should be checked for errors and inconsistencies and checked against the norms and standards of the field.

However, one should remember that mass education is aimed at students of average capacity and that not all students are always equally capable of learning through insight. Also, students need to be prepared to gain the ability and potential to have fruitful insights.  

Learning purely from stimulus-response conditioning is insufficient for progress and major breakthroughs to be made in the sciences. For breakthroughs to be made, humans need to be increasingly capable of higher and higher levels of abstract thinking.

However, we are not all equally capable of having epiphanies on the cutting edge of scientific research. Most education aims to elevate average reasoning, knowledge, and skill acquisition. For insight, learning must build on rather than replace behaviorist teaching practices.

Related posts:

• The Psychology of Long Distance Relationships
• Beck’s Depression Inventory (BDI Test)
• Operant Conditioning (Examples + Research)
• Variable Interval Reinforcement Schedule (Examples)
• Concrete Operational Stage (3rd Cognitive Development)

Reference this article:

About The Author

Operant Conditioning

Classical Conditioning

Observational Learning

Latent Learning

Experiential Learning

The Little Albert Study

Bobo Doll Experiment

Spacing Effect

Von Restorff Effect

PracticalPie.com is a participant in the Amazon Associates Program. As an Amazon Associate we earn from qualifying purchases.

Follow Us On:

Youtube Facebook Instagram X/Twitter

Psychology Resources

Developmental

Personality

Relationships

Psychologists

Serial Killers

Psychology Tests

Personality Quiz

Memory Test

Depression test

Type A/B Personality Test

© PracticalPsychology. All rights reserved

Privacy Policy | Terms of Use

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

6.8: Blocks to Problem Solving

• Last updated
• Save as PDF
• Page ID 54768

• Mehgan Andrade and Neil Walker
• College of the Canyons

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Sometimes, previous experience or familiarity can even make problem solving more difficult. This is the case whenever habitual directions get in the way of finding new directions – an effect called fixation.

Functional Fixedness

Functional fixedness concerns the solution of object-use problems. The basic idea is that when the usual way of using an object is emphasised, it will be far more difficult for a person to use that object in a novel manner. An example for this effect is the candle problem : Imagine you are given a box of matches, some candles and tacks. On the wall of the room there is a cork- board. Your task is to fix the candle to the cork-board in such a way that no wax will drop on the floor when the candle is lit. – Got an idea?

Explanation: The clue is just the following: when people are confronted with a problem

and given certain objects to solve it, it is difficult for them to figure out that they could use them in a different (not so familiar or obvious) way. In this example the box has to be recognized as a support rather than as a container.

A further example is the two-string problem: Knut is left in a room with a chair and a pair of pliers given the task to bind two strings together that are hanging from the ceiling. The problem he faces is that he can never reach both strings at a time because they are just too far away from each other. What can Knut do?

Solution: Knut has to recognize he can use the pliers in a novel function – as weight for a pendulum. He can bind them to one of the strings, push it away, hold the other string and just wait for the first one moving towards him. If necessary, Knut can even climb on the chair, but he is not that small, we suppose…

Mental Fixedness

Functional fixedness as involved in the examples above illustrates a mental set - a person’s tendency to respond to a given task in a manner based on past experience. Because Knut maps an object to a particular function he has difficulties to vary the way of use (pliers as pendulum's weight). One approach to studying fixation was to study wrong-answer verbal insight problems. It was shown that people tend to give rather an incorrect answer when failing to solve a problem than to give no answer at all.

A typical example: People are told that on a lake the area covered by water lilies doubles every 24 hours and that it takes 60 days to cover the whole lake. Then they are asked how many days it takes to cover half the lake. The typical response is '30 days' (whereas 59 days is correct).

These wrong solutions are due to an inaccurate interpretation, hence representation, of the problem. This can happen because of sloppiness (a quick shallow reading of the problemand/or weak monitoring of their efforts made to come to a solution). In this case error feedback should help people to reconsider the problem features, note the inadequacy of their first answer, and find the correct solution. If, however, people are truly fixated on their incorrect representation, being told the answer is wrong does not help. In a study made by P.I. Dallop and R.L. Dominowski in 1992 these two possibilities were contrasted. In approximately one third of the cases error feedback led to right answers, so only approximately one third of the wrong answers were due to inadequate monitoring. [6] Another approach is the study of examples with and without a preceding analogous task. In cases such like the water-jug task analogous thinking indeed leads to a correct solution, but to take a different way might make the case much simpler:

Imagine Knut again, this time he is given three jugs with different capacities and is asked to measure the required amount of water. Of course he is not allowed to use anything despite the jugs and as much water as he likes. In the first case the sizes are 127 litres, 21 litres and 3 litres while 100 litres are desired. In the second case Knut is asked to measure 18 litres from jugs of 39, 15 and three litres size.

In fact participants faced with the 100 litre task first choose a complicate way in order tosolve the second one. Others on the contrary who did not know about that complex task solved the 18 litre case by just adding three litres to 15.

Pitfalls to Problem Solving

Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Albert Einstein once said, “Insanity is doing the same thing over and over again and expecting a different result.” Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but she just needs to go to another doorway, instead of trying to get out through the locked doorway. A mental set is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now. Functional fixedness is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. During the Apollo 13 mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.

Link to Learning

Check out this Apollo 13 scene where the group of NASA engineers are given the task of overcoming functional fixedness.

Researchers have investigated whether functional fixedness is affected by culture. In one experiment, individuals from the Shuar group in Ecuador were asked to use an object for a purpose other than that for which the object was originally intended. For example, the participants were told a story about a bear and a rabbit that were separated by a river and asked to select among various objects, including a spoon, a cup, erasers, and so on, to help the animals. The spoon was the only object long enough to span the imaginary river, but if the spoon was presented in a way that reflected its normal usage, it took participants longer to choose the spoon to solve the problem. (German & Barrett, 2005). The researchers wanted to know if exposure to highly specialized tools, as occurs with individuals in industrialized nations, affects their ability to transcend functional fixedness. It was determined that functional fixedness is experienced in both industrialized and non-industrialized cultures (German & Barrett, 2005).

Common obstacles to solving problems

The example also illustrates two common problems that sometimes happen during problem solving. One of these is functional fixedness : a tendency to regard the functions of objects and ideas as fixed (German & Barrett, 2005). Over time, we get so used to one particular purpose for an object that we overlook other uses. We may think of a dictionary, for example, as necessarily something to verify spellings and definitions, but it also can function as a gift, a doorstop, or a footstool. For students working on the nine-dot matrix described in the last section, the notion of “drawing” a line was also initially fixed; they assumed it to be connecting dots but not extending lines beyond the dots. Functional fixedness sometimes is also called response set , the tendency for a person to frame or think about each problem in a series in the same way as the previous problem, even when doing so is not appropriate to later problems. In the example of the nine-dot matrix described above, students often tried one solution after another, but each solution was constrained by a set response not to extend any line beyond the matrix.

Functional fixedness and the response set are obstacles in problem representation , the way that a person understands and organizes information provided in a problem. If information is misunderstood or used inappropriately, then mistakes are likely—if indeed the problem can be solved at all. With the nine-dot matrix problem, for example, construing the instruction to draw four lines as meaning “draw four lines entirely within the matrix” means that the problem simply could not be solved. For another, consider this problem: “The number of water lilies on a lake doubles each day. Each water lily covers exactly one square foot. If it takes 100 days for the lilies to cover the lake exactly, how many days does it take for the lilies to cover exactly half of the lake?” If you think that the size of the lilies affects the solution to this problem, you have not represented the problem correctly. Information about lily size is not relevant to the solution, and only serves to distract from the truly crucial information, the fact that the lilies double their coverage each day. (The answer, incidentally, is that the lake is half covered in 99 days; can you think why?)

The Systematic Problem-Solving (SPS) Method:

Make better decisions tom g. stevens phd.

Solving problems is important in every area of human thinking. Learning general problem-solving skills can therefore help you improve your ability to cope with every area of your life. All disciplines of philosophy, business, science, and humanities have developed their own approach to solving problems. Remarkably, the problem-solving models developed by each of these areas are strikingly similar. I describe a simple problem-solving process that you can use to solve almost all problems.

Stages of the problem-solving process. The famous psychologist, Dr. Carl Rogers, was one of the first to help us understand how important self-exploration and problem-solving are for overcoming all types of personal, psychological, and daily-living problems. (1);

Consciously going through each of these four stages when solving any complex problem can be very useful. Following are the five stages of the problem-solving method.

STAGE 1: EXPLORATION OF THE PROBLEM

STAGE 2: EXPLORING ALTERNATIVE SOLUTIONS (Routes to Happiness);

STAGE 3: CHOOSING THE BEST ALTERNATIVE

STAGE 4: PLANNING AND ACTION

STAGE 5: EXPERIMENTING AND GATHERING FEEDBACK

During this stage, we gather all of the information we can about both external aspects of the problem and internal aspects. Good information gathering is not an easy process. Scientists spend their whole lives trying to learn about some very small piece of the world. The type of information-gathering process we use will depend upon the type of problem we are trying to solve. For information about the world the following are powerful skills to use.

•  Library reference skills
•  Observational skills
•  Informational interviewing skills
•  Critical thinking skills
•  Scientific method skills
•  Data analysis and statistical skills

Learning how to become an expert at identifying problems and finding causes is essential to become an expert in any field. The above skills are useful in solving many types of problems--even intra-personal ones. However, the focus of this book is how to be happy; and the key to happiness almost always involves not just external causes but internal ones as well.

It is usually much easier for most of us to observe an external event than an internal one. We have our external sensory organs to see and hear external events, but not internal ones. How do we observe that which we cannot see? We can learn to be better observers of our emotions, self-talk, and images.

The self-exploration process described above provides enough information to make you an expert at self-exploration. That is one of the most essential parts of developing your own inner therapist.

STAGE 2: EXPLORING ALTERNATIVE SOLUTIONS OR ROUTES TO HAPPINESS

Gather all the best information you can about possible solutions. Use brainstorming techniques, observe and consult with people who have overcome similar problems, read relevant material, consult experts, and recall your own relevant past experience. Look at both internal and external solutions.

Once you learn so many different routes to happiness, then you will be truly free to choose to be happy in almost any situation you face in life. The actual choice is made in stage 3 of the /problem-solving process. The appendix contains a very useful decision-making model for helping you make complex choices such as choosing a career or relationship. The following is a simple approach to making a decision between alternatives. (See Carkhuff Decision-Making Model, below, for a method for making complex decisions--for career or life planning.);

(1); List all the alternatives you are considering

(2); List all of the values or criteria that will be affected by the decision

(3); Evaluate each alternative by each criteria or value

(4); Choose the alternative which you predict will satisfy the criteria the best and lead to your greatest overall happiness

STAGE 4:  PLANNING AND ACTION (Experimenting);

Many decisions are made, but never implemented. See that you follow-up with good planning. Once you have made your choice, you can use some of the planning methods suggested in the O-PATSM method from chapter 11 to make sure that you follow through with your decision.

This is the stage of acting on your decision. Many people fear making mistakes and failure as if these were some terrible sins that they should never commit. That view of life of life makes every decision and action seem very serious and they often become very timid people who lack creativity and are plagued by guilt and fear of failure. Instead we can view every action as an experiment. If one of our overall goals in life is learning and growth, then we can never fail to learn. All people who have accomplished great happiness for themselves and contributed to others have shared the courage to act on their beliefs.

STAGE 5: GATHERING FEEDBACK

Many people hate to be evaluated and dread finding out the results of what they have done out of fear that the feedback will be negative. These fears can be serious impediments to the growth that can only happen through getting open, accurate feedback.

However, once learning and growth are important goals, then getting feedback becomes highly desirable. How else can we learn? Even negative outcomes can provide valuable information. Of course, almost everyone would rather have outcomes that maximize happiness; but when we don't, we can at least try to maximize our learning. Learning can help maximize happiness in the future.

We can also make the mistakes of dwelling on past mistakes that goes beyond constructive learning and reasonable reparations to victims and of punishing ourselves unnecessarily. Normally, there is no value to punishment--once a lesson has been learned. (2); Keep clear at all times that this problem-solving process is only a tool to serve the overall life goals of increased health, growth, and happiness.

CARKHUFF DECISION-MAKING MODEL:   This particular decision-making model is based upon one by Dr. Robert Carkhuff and follows the general guidelines of a considerable amount of research on how people can make more effective decisions. It can also be used for any other type of decision--from buying a new car to choosing a mate.

EXAMPLE OF USING THE DECISION-MAKING MODEL

The decision-making model will be illustrated in a way which you can use aa an analogy for making your own career decision. In this example, Henry is trying to decide whether to major in psychology or in computer science. Thus he has narrowed his alternatives to the following two:

1); majoring in psychology with a career goal of either going into high school counseling or teaching or 2); majoring in computer science with a possible goal of working as a computer programmer.

These are represented along the top axis of the following matrix.

  ** is the WINNER-it has the most points of the two alternatives

STEPS TO USING THE DECISION-MAKING MODEL--(use above example);

STEP 1-- LIST YOUR CAREER ALTERNATIVES. This is your refined list of alternatives of which majors or occupations you are trying to decide between. Remember, that you can list as many as you want. You can list unusual combinations of simpler alternatives. For Henry those narrowed alternatives were psychology and computer science.

STEP 2--CAREER SELECTION CRITERIA. Review your Career Selection Criteria list and write all the important career selection criteria in the far left column. Note that repeating the same idea or leaving out an important idea can affect the decision outcome.

STEP 3-- CRITERIA WEIGHTS. Evaluate the relative importance to you of each of your Career Selection Criteria on a scale of 1 to 10 (10 being the most important);. Write your answer in the column next to the selection criteria.

STEP 4--ALTERNATIVE EVALUATION SCALE. Each alternative is to be evaluated from the point of view of each selection criterion. You need to think about what this means for each selection criterion. For example Henry determined that for the selection criteria of income , a "minimally acceptable" income would be $25,000 starting with prospects of making up to $50,000 eventually. An outstanding salary would be starting at about $40, 000 with prospects of making up to $100,000.

+5 = Maximum evaluation--outstanding (example: income begin $40,000 go to $100,000 +4, +3, +2, +1 = intermediate values

0 = Minimally acceptable value. (example: income = begin $20,000 go to $45,000);

-1, -2, -3, -4 = intermediate values

-5 = Minimum evaluation--worst possible (example: income < $10,000

STEP 5--EVALUATE EACH ALTERNATIVE BY EACH SELECTION CRITERION. Use the evaluation scale from step 3 to evaluate each alternative from the point of view of each Career Selection Criterion. Give it rating from -5 to +5. In the example above, both alternatives were evaluated on the criterion of "income": Henry gave the psychology income an evaluation of "+2" and computer science income an evaluation of " +4."

STEP 6--MULTIPLY THE CRITERIA WEIGHTS TIMES THE EVALUATIONS. In the example above for the selection criterion of "income," Henry multiplied the criterion weight of "9" times the evaluation of " +2" for "PSYCH" to get a result of "18." That is its SCORE OR POINTS for psychology on the criterion of income. Put it inside of the parentheses. This score of 18 is an overall prediction much Henry's income in psychology will contribute to his overall happiness. Since he had a score of 36 in computer science, he his predicting that he will be much happier with his income in that field.

STEP 7--FIND THE OVERALL SUM OF THE SCORES FOR EACH ALTERNATIVE. Add together the numbers inside the parentheses for each alternative. In the example above, the overall sum for the "PSYCH" alternative is "405."

STEP 8--COMPARE THE ALTERNATIVES WITH EACH OTHER AND WITH THE "IDEAL." The "ideal" is the maximum possible number of points. Once you have determined all the totals and compared them to each other, try to figure out why one alternative came out ahead of another--where it got its points. Play with the points until you think the points match your true feelings and values.

* The alternative with the most points is the one you are predicting will make you the happiest person.

1. 1 Some might argue that Freud was the first. He clearly did describe many helpful techniques. I think that some of his free association techniques are still very useful for helping to find underlying beliefs, images, or cognitive systems which are related to the problem. However, Rogers was the one that more clearly described the stages of self-exploration and problem-solving and the conditions of unconditional positive regard, empathetic understanding, and genuineness on the part of the therapist which seem to be important to the therapeutic process or to any person attempting to feel better.

Robert Carkhuff (one of Roger's pupils); has developed a structured training system for helping people learn these skills. Robert Cash, a personal friend, has further elaborated these skills in his own courses and introduced me to this process. There is a good deal of research supporting the effectiveness of these techniques.

2. 2 This statement does not address the use of punishment as a deterrent to prevent some persons from profiting from their dysfunctional behaviors. For example if behaviors such as murder, robbery, or selling drugs are not given sufficient punishment, some people will engage in these behaviors. A person whose ultimate concern is money and pleasure may deal drugs to make money with little regard to how it affects others. Increasing the cost for a person with those beliefs can reduce the chances they will sell drugs.

Self-Help and other resources on this website (and site map)

Copyright 2021 Tom G. Stevens PhD  

7. Thinking and Intelligence

Problem solving, learning objectives.

By the end of this section, you will be able to:

• Describe problem solving strategies
• Define algorithm and heuristic
• Explain some common roadblocks to effective problem solving

People face problems every day—usually, multiple problems throughout the day. Sometimes these problems are straightforward: To double a recipe for pizza dough, for example, all that is required is that each ingredient in the recipe be doubled. Sometimes, however, the problems we encounter are more complex. For example, say you have a work deadline, and you must mail a printed copy of a report to your supervisor by the end of the business day. The report is time-sensitive and must be sent overnight. You finished the report last night, but your printer will not work today. What should you do? First, you need to identify the problem and then apply a strategy for solving the problem.

PROBLEM-SOLVING STRATEGIES

When you are presented with a problem—whether it is a complex mathematical problem or a broken printer, how do you solve it? Before finding a solution to the problem, the problem must first be clearly identified. After that, one of many problem solving strategies can be applied, hopefully resulting in a solution.

A problem-solving strategy is a plan of action used to find a solution. Different strategies have different action plans associated with them ( [link] ). For example, a well-known strategy is trial and error . The old adage, “If at first you don’t succeed, try, try again” describes trial and error. In terms of your broken printer, you could try checking the ink levels, and if that doesn’t work, you could check to make sure the paper tray isn’t jammed. Or maybe the printer isn’t actually connected to your laptop. When using trial and error, you would continue to try different solutions until you solved your problem. Although trial and error is not typically one of the most time-efficient strategies, it is a commonly used one.

Another type of strategy is an algorithm. An algorithm is a problem-solving formula that provides you with step-by-step instructions used to achieve a desired outcome (Kahneman, 2011). You can think of an algorithm as a recipe with highly detailed instructions that produce the same result every time they are performed. Algorithms are used frequently in our everyday lives, especially in computer science. When you run a search on the Internet, search engines like Google use algorithms to decide which entries will appear first in your list of results. Facebook also uses algorithms to decide which posts to display on your newsfeed. Can you identify other situations in which algorithms are used?

A heuristic is another type of problem solving strategy. While an algorithm must be followed exactly to produce a correct result, a heuristic is a general problem-solving framework (Tversky & Kahneman, 1974). You can think of these as mental shortcuts that are used to solve problems. A “rule of thumb” is an example of a heuristic. Such a rule saves the person time and energy when making a decision, but despite its time-saving characteristics, it is not always the best method for making a rational decision. Different types of heuristics are used in different types of situations, but the impulse to use a heuristic occurs when one of five conditions is met (Pratkanis, 1989):

• When one is faced with too much information
• When the time to make a decision is limited
• When the decision to be made is unimportant
• When there is access to very little information to use in making the decision
• When an appropriate heuristic happens to come to mind in the same moment

Working backwards is a useful heuristic in which you begin solving the problem by focusing on the end result. Consider this example: You live in Washington, D.C. and have been invited to a wedding at 4 PM on Saturday in Philadelphia. Knowing that Interstate 95 tends to back up any day of the week, you need to plan your route and time your departure accordingly. If you want to be at the wedding service by 3:30 PM, and it takes 2.5 hours to get to Philadelphia without traffic, what time should you leave your house? You use the working backwards heuristic to plan the events of your day on a regular basis, probably without even thinking about it.

Another useful heuristic is the practice of accomplishing a large goal or task by breaking it into a series of smaller steps. Students often use this common method to complete a large research project or long essay for school. For example, students typically brainstorm, develop a thesis or main topic, research the chosen topic, organize their information into an outline, write a rough draft, revise and edit the rough draft, develop a final draft, organize the references list, and proofread their work before turning in the project. The large task becomes less overwhelming when it is broken down into a series of small steps.

Problem-solving abilities can improve with practice. Many people challenge themselves every day with puzzles and other mental exercises to sharpen their problem-solving skills. Sudoku puzzles appear daily in most newspapers. Typically, a sudoku puzzle is a 9×9 grid. The simple sudoku below ( [link] ) is a 4×4 grid. To solve the puzzle, fill in the empty boxes with a single digit: 1, 2, 3, or 4. Here are the rules: The numbers must total 10 in each bolded box, each row, and each column; however, each digit can only appear once in a bolded box, row, and column. Time yourself as you solve this puzzle and compare your time with a classmate.

How long did it take you to solve this sudoku puzzle? (You can see the answer at the end of this section.)

Here is another popular type of puzzle ( [link] ) that challenges your spatial reasoning skills. Connect all nine dots with four connecting straight lines without lifting your pencil from the paper:

Did you figure it out? (The answer is at the end of this section.) Once you understand how to crack this puzzle, you won’t forget.

Take a look at the “Puzzling Scales” logic puzzle below ( [link] ). Sam Loyd, a well-known puzzle master, created and refined countless puzzles throughout his lifetime (Cyclopedia of Puzzles, n.d.).

PITFALLS TO PROBLEM SOLVING

Not all problems are successfully solved, however. What challenges stop us from successfully solving a problem? Albert Einstein once said, “Insanity is doing the same thing over and over again and expecting a different result.” Imagine a person in a room that has four doorways. One doorway that has always been open in the past is now locked. The person, accustomed to exiting the room by that particular doorway, keeps trying to get out through the same doorway even though the other three doorways are open. The person is stuck—but she just needs to go to another doorway, instead of trying to get out through the locked doorway. A mental set is where you persist in approaching a problem in a way that has worked in the past but is clearly not working now.

Functional fixedness is a type of mental set where you cannot perceive an object being used for something other than what it was designed for. During the Apollo 13 mission to the moon, NASA engineers at Mission Control had to overcome functional fixedness to save the lives of the astronauts aboard the spacecraft. An explosion in a module of the spacecraft damaged multiple systems. The astronauts were in danger of being poisoned by rising levels of carbon dioxide because of problems with the carbon dioxide filters. The engineers found a way for the astronauts to use spare plastic bags, tape, and air hoses to create a makeshift air filter, which saved the lives of the astronauts.

Link to Learning

Check out this Apollo 13 scene where the group of NASA engineers are given the task of overcoming functional fixedness.

Researchers have investigated whether functional fixedness is affected by culture. In one experiment, individuals from the Shuar group in Ecuador were asked to use an object for a purpose other than that for which the object was originally intended. For example, the participants were told a story about a bear and a rabbit that were separated by a river and asked to select among various objects, including a spoon, a cup, erasers, and so on, to help the animals. The spoon was the only object long enough to span the imaginary river, but if the spoon was presented in a way that reflected its normal usage, it took participants longer to choose the spoon to solve the problem. (German & Barrett, 2005). The researchers wanted to know if exposure to highly specialized tools, as occurs with individuals in industrialized nations, affects their ability to transcend functional fixedness. It was determined that functional fixedness is experienced in both industrialized and nonindustrialized cultures (German & Barrett, 2005).

In order to make good decisions, we use our knowledge and our reasoning. Often, this knowledge and reasoning is sound and solid. Sometimes, however, we are swayed by biases or by others manipulating a situation. For example, let’s say you and three friends wanted to rent a house and had a combined target budget of $1,600. The realtor shows you only very run-down houses for $1,600 and then shows you a very nice house for $2,000. Might you ask each person to pay more in rent to get the $2,000 home? Why would the realtor show you the run-down houses and the nice house? The realtor may be challenging your anchoring bias. An anchoring bias occurs when you focus on one piece of information when making a decision or solving a problem. In this case, you’re so focused on the amount of money you are willing to spend that you may not recognize what kinds of houses are available at that price point.

The confirmation bias is the tendency to focus on information that confirms your existing beliefs. For example, if you think that your professor is not very nice, you notice all of the instances of rude behavior exhibited by the professor while ignoring the countless pleasant interactions he is involved in on a daily basis. Hindsight bias leads you to believe that the event you just experienced was predictable, even though it really wasn’t. In other words, you knew all along that things would turn out the way they did. Representative bias describes a faulty way of thinking, in which you unintentionally stereotype someone or something; for example, you may assume that your professors spend their free time reading books and engaging in intellectual conversation, because the idea of them spending their time playing volleyball or visiting an amusement park does not fit in with your stereotypes of professors.

Finally, the availability heuristic is a heuristic in which you make a decision based on an example, information, or recent experience that is that readily available to you, even though it may not be the best example to inform your decision . Biases tend to “preserve that which is already established—to maintain our preexisting knowledge, beliefs, attitudes, and hypotheses” (Aronson, 1995; Kahneman, 2011). These biases are summarized in [link] .

Please visit this site to see a clever music video that a high school teacher made to explain these and other cognitive biases to his AP psychology students.

Were you able to determine how many marbles are needed to balance the scales in [link] ? You need nine. Were you able to solve the problems in [link] and [link] ? Here are the answers ( [link] ).

Many different strategies exist for solving problems. Typical strategies include trial and error, applying algorithms, and using heuristics. To solve a large, complicated problem, it often helps to break the problem into smaller steps that can be accomplished individually, leading to an overall solution. Roadblocks to problem solving include a mental set, functional fixedness, and various biases that can cloud decision making skills.

Self Check Questions

Critical thinking questions.

1. What is functional fixedness and how can overcoming it help you solve problems?

2. How does an algorithm save you time and energy when solving a problem?

Personal Application Question

3. Which type of bias do you recognize in your own decision making processes? How has this bias affected how you’ve made decisions in the past and how can you use your awareness of it to improve your decisions making skills in the future?

1. Functional fixedness occurs when you cannot see a use for an object other than the use for which it was intended. For example, if you need something to hold up a tarp in the rain, but only have a pitchfork, you must overcome your expectation that a pitchfork can only be used for garden chores before you realize that you could stick it in the ground and drape the tarp on top of it to hold it up.

2. An algorithm is a proven formula for achieving a desired outcome. It saves time because if you follow it exactly, you will solve the problem without having to figure out how to solve the problem. It is a bit like not reinventing the wheel.

• Psychology. Authored by : OpenStax College. Located at : http://cnx.org/contents/[email protected]:1/Psychology . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/content/col11629/latest/.

From Dilemmas to Solutions: Problem-Solving Examples to Learn From

• By Daria Burnett
• May 21, 2023

Introduction to Problem-Solving

Life is full of challenges and dilemmas, both big and small.

But if there’s one skill that can help you navigate these, it’s problem-solving .

So, what exactly is problem-solving? And why is it such a crucial skill in daily life?

Understanding the Concept of Problem-Solving

Problem-solving is a mental process that involves identifying, analyzing, and resolving challenges or difficulties.

It’s like a journey that starts with a problem and ends with a solution.

It’s a skill that’s not just used in the field of psychology but in all aspects of life.

Whether you’re trying to decide on the best route to work, dealing with a disagreement with a friend, or figuring out how to fix a leaky faucet, you’re using your problem-solving skills.

When you’re faced with a problem, your brain goes through a series of steps to find a solution.

This process can be conscious or unconscious and can involve logical thinking, creativity, and prior knowledge.

Effective problem-solving can lead to better decisions and outcomes, making it a valuable tool in your personal and professional life.

Related Posts:

• Harnessing Behavior: Empowering Positive Punishment Examples
• Exploring Different Manager Coaching Styles: What Works Best for You?
• From Basics to Brilliance: Exploring What Shaping Entails in Psychology

Importance of Problem-Solving in Daily Life

Why is problem-solving so important in daily life? Well, it’s simple.

Problems are a part of life.

They arise in different shapes and sizes, and in different areas of life, including work, relationships, health, and personal growth.

Having strong problem-solving skills can help you navigate these challenges effectively and efficiently.

In your personal life, problem-solving can help you manage stress and conflict, make better decisions, and achieve your goals.

In the workplace, it can help you navigate complex projects, improve processes, and foster innovation.

Problem-solving is also a key skill in many professions and industries, from engineering and science to healthcare and customer service.

Moreover, problem-solving can contribute to your overall mental well-being.

It can give you a sense of control and agency, reduce feelings of stress and anxiety, and foster a positive attitude.

It’s also a key component of resilience, the ability to bounce back from adversity.

In conclusion, problem-solving is a fundamental skill in life.

It’s a tool you can use to tackle challenges, make informed decisions, and drive change.

By understanding the concept of problem-solving and recognizing its importance in daily life, you’re taking the first step toward becoming a more effective problem solver.

As we delve deeper into this topic, you’ll discover practical problem-solving examples, learn about different problem-solving techniques, and gain insights on how to improve your own problem-solving skills.

So, stay tuned and continue your exploration of introduction to psychology with us.

Stages of Problem-Solving

The process of problem-solving can be broken down into three key stages: identifying the problem , developing possible solutions , and implementing the best solution .

Each stage requires a different set of skills and strategies.

By understanding these stages, you can enhance your problem-solving abilities and tackle various challenges more effectively.

Identifying the Problem

The first step in problem-solving is recognizing that a problem exists.

This involves defining the issue clearly and understanding its root cause.

You might need to gather information, ask questions, and analyze the situation from multiple perspectives.

It can be helpful to write down the problem and think about how it impacts you or others involved.

For instance, if you’re struggling with time management, the problem might be that you have too many obligations and not enough time.

Or perhaps your methods of organizing your tasks aren’t effective.

It’s important to be as specific as possible when identifying the problem, as this will guide the rest of the problem-solving process.

Developing Possible Solutions

Once you’ve identified the problem, the next step is to brainstorm possible solutions.

This is where creativity comes into play.

Don’t limit yourself; even ideas that seem unrealistic or out of the box can lead to effective solutions.

Consider different strategies and approaches.

You could try using techniques like mind mapping, listing pros and cons, or consulting with others for fresh perspectives.

Remember, the goal is to generate a variety of options, not to choose a solution at this stage.

Implementing the Best Solution

The final stage of problem-solving is to select the best solution and put it into action.

Review the options you’ve developed, evaluate their potential effectiveness, and make a decision.

Keep in mind that the “best” solution isn’t necessarily the perfect one (as there might not be a perfect solution), but rather the one that seems most likely to achieve your desired outcome given the circumstances.

Once you’ve chosen a solution, plan out the steps needed to implement it and then take action.

Monitor the results and adjust your approach as necessary.

If the problem persists, don’t be discouraged; return to the previous stages, reassess the problem and your potential solutions, and try again.

Remember, problem-solving is a dynamic process that often involves trial and error.

It’s an essential skill in many areas of life, from everyday challenges to workplace dilemmas.

To learn more about the psychology behind problem-solving and decision-making, check out our introduction to psychology article.

Problem-Solving Examples

Understanding the concept of problem-solving is one thing, but seeing it in action is another.

To help you grasp the practical application of problem-solving strategies, let’s explore three different problem-solving examples from daily life, the workplace, and relationships.

Daily Life Problem-Solving Example

Imagine you’re trying to lose weight but struggle with late-night snacking.

The issue isn’t uncommon, but it’s hindering your progress towards your weight loss goal.

• Identifying the Problem : Late-night snacking is causing you to consume extra calories, preventing weight loss.
• Developing Possible Solutions : You could consider eating an earlier dinner, having a healthier snack option, or practicing mindful eating.
• Implementing the Best Solution : After trying out different solutions, you find that preparing a healthy snack in advance minimizes your calorie intake and satisfies your late-night cravings, helping you stay on track with your weight loss goal.

Workplace Problem-Solving Example

Let’s consider a scenario where a team at work is failing to meet project deadlines consistently.

• Identifying the Problem : The team is not completing projects on time, causing delays in the overall project timeline.
• Developing Possible Solutions : The team could consider improving their time management skills, using project management tools, or redistributing tasks among team members.
• Implementing the Best Solution : After trying out different strategies, the team finds that using a project management tool helps them stay organized, delegate tasks effectively, and complete projects within the given timeframe.

For more insights on effective management styles that can help in problem-solving at the workplace, check out our articles on autocratic leadership , democratic leadership style , and laissez faire leadership .

Relationship Problem-Solving Example

In a romantic relationship, conflicts can occasionally arise.

Let’s imagine a common issue where one partner feels the other isn’t spending enough quality time with them.

• Identifying the Problem : One partner feels neglected due to a lack of quality time spent together.
• Developing Possible Solutions : The couple could consider scheduling regular date nights, engaging in shared hobbies, or setting aside a specific time each day for undisturbed conversation.
• Implementing the Best Solution : The couple decides to implement a daily “unplugged” hour where they focus solely on each other without distractions. This results in improved relationship satisfaction.

For more on navigating relationship challenges, check out our articles on anxious avoidant attachment and emotional awareness .

These problem-solving examples illustrate how the process of identifying a problem, developing possible solutions, and implementing the best solution can be applied to various situations.

By understanding and applying these strategies, you can improve your problem-solving skills and navigate challenges more effectively.

Techniques for Effective Problem-Solving

As you navigate the world of problem-solving, you’ll find that there are multiple techniques you can use to arrive at a solution.

Each technique offers a unique approach to identifying issues, generating potential solutions, and choosing the best course of action.

In this section, we’ll explore three common techniques: Brainstorming , Root Cause Analysis , and SWOT Analysis .

Brainstorming

Brainstorming is a free-thinking method used to generate a large number of ideas related to a specific problem.

You do this by suspending criticism and allowing your creativity to flow.

The aim is to produce as many ideas as possible, even if they seem far-fetched.

You then evaluate these ideas to identify the most beneficial solutions.

By using brainstorming, you can encourage out-of-the-box thinking and possibly discover innovative solutions to challenging problems.

Root Cause Analysis

Root Cause Analysis (RCA) is a method used to identify the underlying causes of a problem.

The goal is to address these root causes rather than the symptoms of the problem.

This technique helps to prevent the same issue from recurring in the future.

There are several RCA methods, such as the “5 Whys” technique, where you ask “why” multiple times until you uncover the root cause of the problem.

By identifying and addressing the root cause, you tackle the problem at its source, which can lead to more effective and long-lasting solutions.

SWOT Analysis

SWOT Analysis is a strategic planning technique that helps you identify your Strengths, Weaknesses, Opportunities, and Threats related to a problem.

This approach encourages you to examine the problem from different angles, helping you understand the resources you have at your disposal (Strengths), the areas where you could improve (Weaknesses), the external factors that could benefit you (Opportunities), and the external factors that could cause problems (Threats).

With this comprehensive understanding, you can develop a well-informed strategy to solve the problem.

Each of these problem-solving techniques provides a distinct approach to identifying and resolving issues.

By understanding and utilizing these methods, you can enhance your problem-solving skills and increase your effectiveness in dealing with challenges.

For more insights into effective problem-solving and other psychological topics, explore our introduction to psychology .

Improving Your Problem-Solving Skills

Learning to solve problems effectively is a skill that can be honed with time and practice.

The following are some ways to enhance your problem-solving capabilities.

Practice Makes Perfect

The saying “practice makes perfect” holds true when it comes to problem-solving.

The more problems you tackle, the better you’ll become at devising and implementing effective solutions.

Seek out opportunities to practice your problem-solving skills both in everyday life and in more complex situations.

This could involve resolving a dispute at work, figuring out a puzzle, or even strategizing in a board game.

Each problem you encounter is a new opportunity to apply and refine your skills.

Learning from Others’ Experiences

There’s much to be gained from observing how others approach problem-solving.

Whether it’s reading about problem solving examples from renowned psychologists or discussing strategies with colleagues, you can learn valuable techniques and perspectives from the experiences of others.

Consider participating in group activities that require problem-solving, such as escape rooms or team projects.

Observe how team members identify problems, brainstorm solutions, and decide on the best course of action.

Embracing a Growth Mindset

A key component of effective problem-solving is adopting a growth mindset.

This mindset, coined by psychologist Carol Dweck, is the belief that abilities and intelligence can be developed through dedication and hard work.

When you embrace a growth mindset, you view challenges as opportunities to learn and grow rather than as insurmountable obstacles.

Believing in your ability to develop and enhance your problem-solving skills over time can make the process less daunting and more rewarding.

So, when you encounter a problem, instead of thinking, “I can’t do this,” try thinking, “I can’t do this yet, but with effort and practice, I can learn.”

For more on the growth mindset, you might want to check out our article on what is intrinsic motivation which includes how a growth mindset can fuel your motivation to improve.

By practicing regularly, learning from others, and embracing a growth mindset, you can continually improve your problem-solving skills and become more adept at overcoming challenges you encounter.

What is Problem Solving? (Steps, Techniques, Examples)

By Status.net Editorial Team on May 7, 2023 — 5 minutes to read

What Is Problem Solving?

Definition and importance.

Problem solving is the process of finding solutions to obstacles or challenges you encounter in your life or work. It is a crucial skill that allows you to tackle complex situations, adapt to changes, and overcome difficulties with ease. Mastering this ability will contribute to both your personal and professional growth, leading to more successful outcomes and better decision-making.

Problem-Solving Steps

The problem-solving process typically includes the following steps:

• Identify the issue : Recognize the problem that needs to be solved.
• Analyze the situation : Examine the issue in depth, gather all relevant information, and consider any limitations or constraints that may be present.
• Generate potential solutions : Brainstorm a list of possible solutions to the issue, without immediately judging or evaluating them.
• Evaluate options : Weigh the pros and cons of each potential solution, considering factors such as feasibility, effectiveness, and potential risks.
• Select the best solution : Choose the option that best addresses the problem and aligns with your objectives.
• Implement the solution : Put the selected solution into action and monitor the results to ensure it resolves the issue.
• Review and learn : Reflect on the problem-solving process, identify any improvements or adjustments that can be made, and apply these learnings to future situations.

Defining the Problem

To start tackling a problem, first, identify and understand it. Analyzing the issue thoroughly helps to clarify its scope and nature. Ask questions to gather information and consider the problem from various angles. Some strategies to define the problem include:

• Brainstorming with others
• Asking the 5 Ws and 1 H (Who, What, When, Where, Why, and How)
• Analyzing cause and effect
• Creating a problem statement

Generating Solutions

Once the problem is clearly understood, brainstorm possible solutions. Think creatively and keep an open mind, as well as considering lessons from past experiences. Consider:

• Creating a list of potential ideas to solve the problem
• Grouping and categorizing similar solutions
• Prioritizing potential solutions based on feasibility, cost, and resources required
• Involving others to share diverse opinions and inputs

Evaluating and Selecting Solutions

Evaluate each potential solution, weighing its pros and cons. To facilitate decision-making, use techniques such as:

• SWOT analysis (Strengths, Weaknesses, Opportunities, Threats)
• Decision-making matrices
• Pros and cons lists
• Risk assessments

After evaluating, choose the most suitable solution based on effectiveness, cost, and time constraints.

Implementing and Monitoring the Solution

Implement the chosen solution and monitor its progress. Key actions include:

• Communicating the solution to relevant parties
• Setting timelines and milestones
• Assigning tasks and responsibilities
• Monitoring the solution and making adjustments as necessary
• Evaluating the effectiveness of the solution after implementation

Utilize feedback from stakeholders and consider potential improvements. Remember that problem-solving is an ongoing process that can always be refined and enhanced.

Problem-Solving Techniques

During each step, you may find it helpful to utilize various problem-solving techniques, such as:

• Brainstorming : A free-flowing, open-minded session where ideas are generated and listed without judgment, to encourage creativity and innovative thinking.
• Root cause analysis : A method that explores the underlying causes of a problem to find the most effective solution rather than addressing superficial symptoms.
• SWOT analysis : A tool used to evaluate the strengths, weaknesses, opportunities, and threats related to a problem or decision, providing a comprehensive view of the situation.
• Mind mapping : A visual technique that uses diagrams to organize and connect ideas, helping to identify patterns, relationships, and possible solutions.

Brainstorming

When facing a problem, start by conducting a brainstorming session. Gather your team and encourage an open discussion where everyone contributes ideas, no matter how outlandish they may seem. This helps you:

• Generate a diverse range of solutions
• Encourage all team members to participate
• Foster creative thinking

When brainstorming, remember to:

• Reserve judgment until the session is over
• Encourage wild ideas
• Combine and improve upon ideas

Root Cause Analysis

For effective problem-solving, identifying the root cause of the issue at hand is crucial. Try these methods:

• 5 Whys : Ask “why” five times to get to the underlying cause.
• Fishbone Diagram : Create a diagram representing the problem and break it down into categories of potential causes.
• Pareto Analysis : Determine the few most significant causes underlying the majority of problems.

SWOT Analysis

SWOT analysis helps you examine the Strengths, Weaknesses, Opportunities, and Threats related to your problem. To perform a SWOT analysis:

• List your problem’s strengths, such as relevant resources or strong partnerships.
• Identify its weaknesses, such as knowledge gaps or limited resources.
• Explore opportunities, like trends or new technologies, that could help solve the problem.
• Recognize potential threats, like competition or regulatory barriers.

SWOT analysis aids in understanding the internal and external factors affecting the problem, which can help guide your solution.

Mind Mapping

A mind map is a visual representation of your problem and potential solutions. It enables you to organize information in a structured and intuitive manner. To create a mind map:

• Write the problem in the center of a blank page.
• Draw branches from the central problem to related sub-problems or contributing factors.
• Add more branches to represent potential solutions or further ideas.

Mind mapping allows you to visually see connections between ideas and promotes creativity in problem-solving.

Examples of Problem Solving in Various Contexts

In the business world, you might encounter problems related to finances, operations, or communication. Applying problem-solving skills in these situations could look like:

• Identifying areas of improvement in your company’s financial performance and implementing cost-saving measures
• Resolving internal conflicts among team members by listening and understanding different perspectives, then proposing and negotiating solutions
• Streamlining a process for better productivity by removing redundancies, automating tasks, or re-allocating resources

In educational contexts, problem-solving can be seen in various aspects, such as:

• Addressing a gap in students’ understanding by employing diverse teaching methods to cater to different learning styles
• Developing a strategy for successful time management to balance academic responsibilities and extracurricular activities
• Seeking resources and support to provide equal opportunities for learners with special needs or disabilities

Everyday life is full of challenges that require problem-solving skills. Some examples include:

• Overcoming a personal obstacle, such as improving your fitness level, by establishing achievable goals, measuring progress, and adjusting your approach accordingly
• Navigating a new environment or city by researching your surroundings, asking for directions, or using technology like GPS to guide you
• Dealing with a sudden change, like a change in your work schedule, by assessing the situation, identifying potential impacts, and adapting your plans to accommodate the change.
• How to Resolve Employee Conflict at Work [Steps, Tips, Examples]
• How to Write Inspiring Core Values? 5 Steps with Examples
• 30 Employee Feedback Examples (Positive & Negative)

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Front Psychol

Problem solving stages in the five square problem

1 Parmenides Center for the Study of Thinking, Pullach, Germany

Eörs Szathmáry

2 Parmenides Center for the Conceptual Foundations of Science, Pullach, Germany

3 MTA-ELTE Theoretical Biology and Evolutionary Ecology Research Group, Biological Institute, Eötvös Loránd University, Budapest, Hungary

Michael Öllinger

4 Psychological Department, Ludwig-Maximilians-University, Munich, Germany

Associated Data

According to the restructuring hypothesis, insight problem solving typically progresses through consecutive stages of search, impasse, insight, and search again for someone, who solves the task. The order of these stages was determined through self-reports of problem solvers and has never been verified behaviorally. We asked whether individual analysis of problem solving attempts of participants revealed the same order of problem solving stages as defined by the theory and whether their subjective feelings corresponded to the problem solving stages they were in. Our participants tried to solve the Five-Square problem in an online task, while we recorded the time and trajectory of their stick movements. After the task they were asked about their feelings related to insight and some of them also had the possibility of reporting impasse while working on the task. We found that the majority of participants did not follow the classic four-stage model of insight, but had more complex sequences of problem solving stages, with search and impasse recurring several times. This means that the classic four-stage model is not sufficient to describe variability on the individual level. We revised the classic model and we provide a new model that can generate all sequences found. Solvers reported insight more often than non-solvers and non-solvers reported impasse more often than solvers, as expected; but participants did not report impasse more often during behaviorally defined impasse stages than during other stages. This shows that impasse reports might be unreliable indicators of impasse. Our study highlights the importance of individual analysis of problem solving behavior to verify insight theory.

Introduction

Insight tasks and the restructuring hypothesis.

Insight tasks are used in cognitive psychology to study insight problem solving (Öllinger and Knoblich, 2009 ). An example is the Five-Square problem (Katona, 1940 ), where problem solvers see a cross shape made of matchsticks (Figure ​ (Figure1) 1 ) and they have to replace three matchsticks in order to get a shape of four squares of equal size instead of the given five squares in the cross shape. According to the restructuring hypothesis, insight problem solving is different from analytic problem solving (Fleck and Weisberg, 2013 ): problem solvers cannot assess how far they are from the solution (Metcalfe and Wiebe, 1987 ), and the solution pops into the problem solvers' mind suddenly and unexpectedly, evoking an Eureka moment, or “Aha!” experience (Durso et al., 1994 ; Wegner, 2002 ). This moment of enlightenment is usually—according to some, necessarily (Ohlsson, 1992 ; Knoblich et al., 1999 , 2001 ; Jones, 2003 ; Öllinger et al., 2014a )—preceded by a longer period of impasse when the problem solver gets stuck and has no idea how to proceed.

The initial position of sticks on the grid in the five square problem . For the solution, see the Supplementary Material. We show a 5-by-5 grid here, but in the computerized task, the cross shape was in the middle of a 9-by-9 grid.

The restructuring hypothesis explains these phenomena by a need for structural change in the mental representation of the problem (Wertheimer, 1959 ; Ohlsson, 1984a , b , 1992 ; Fleck and Weisberg, 2013 ). When the problem solver starts working on the task, the candidate solutions that the problem solver considers are unnecessarily constrained by some false assumptions about the task. The search space in which the person is looking for the solution does not contain the solution, because it is overly restricted. For example, in the Five-Square problem, most problem solvers start placing sticks to positions that touch original stick positions, i.e., they do not consider putting sticks further away from the initial shape. According to Öllinger et al. ( 2014a ), they are constrained by the false assumption that the shape should stay in one piece. After failing several times, the problem solver reaches an impasse and feels that there is no way to get closer to the solution (Ohlsson, 1992 ). During an impasse problem solvers either do nothing or they repeat previous attempts to solve the task (Beeftink et al., 2008 ). Those people who do not solve the task get stuck in this state, while others overcome the self-imposed constraints. The latter start to look for the solution in an extended search space, in which, eventually they find the solution (in the Five-Square problem, they start putting sticks to further positions, and decompose the initial cross shape). Overcoming constraints and restructuring the task in one's mind is often accompanied by an “Aha!” experience that is usually used as the defining feature of insight problem solving (Bowden and Beeman, 1998 ; Boden, 2004 ; Bowden et al., 2005 ; Kounios et al., 2006 ; Danek et al., 2013 , 2014 ).

Levels of description of problem solving stages

The reader might have realized that in the description above, problem solving stages are sometimes described by the cognitive process that supposedly goes on in the problem solver's mind (Wallas, 1926 ), other times by what the problem solver does or feels (Danek et al., 2014 ). We see a lack of clarity in this regard in the literature, so here we would like to disentangle the different levels of description, and identify which phenomena belong to the cognitive, behavioral and affective level (Table ​ (Table1 1 ).

Three levels of description of insight problem solving stages for a successful problem solver who goes through restructuring .

The first stage is most often described on the behavioral level: the problem solver repeatedly attempts to solve the task, but fails. The underlying cognitive process is supposed to be conscious search in the initial, constrained search space (e.g., MacGregor et al., 2001 ). The second stage, impasse, is usually identified by mental states: frustration, feeling being stuck, not knowing how to proceed (Ohlsson, 1992 ; Danek et al., 2014 ). People who cannot solve the task get stuck in this stage. Its behavioral correlates are either inactivity, or repeating previous moves or candidate solutions (Ohlsson, 1992 ; Jones, 2003 ; Beeftink et al., 2008 ). We do not know what happens during impasse on the cognitive level but we hypothesize that there is an underlying unconscious search process that could result in lifting the constraints of the initial search space (Metcalfe and Wiebe, 1987 ; Bowers et al., 1990 ; Seifert et al., 1994 ; Bowden and Beeman, 1998 ; Kounios and Beeman, 2014 ). According to others, incubation is important in this process (Seifert et al., 1994 ; Beeftink et al., 2008 ): taking breaks from the task increases solution rate. Recently, Dietrich and Haider ( 2014 ) and Fernando et al. ( 2010 ) proposed that the underlying search might be evolutionary and parallel in nature. That means that several search processes are launched at the same time and their results are tested against a criterion of success (fitness function). The most promising candidates are copied, and modified until a solution is found or a dead-end is reached. The third stage, insight, is named after its affective correlate, but its most important feature is the cognitive process of representational change, or restructuring (Knoblich et al., 1999 ). Its behavioral correlate (or rather causal effect) is sometimes identified as the critical move—the first move that goes outside the restricted search space (Jones, 2003 ). The fourth stage is conscious search again, but now, in the extended search space, at the end of which the problem solver finds the solution (Öllinger et al., 2014b ). The fourth stage could be very brief (depending on the problem) because problem solvers often find the solution shortly after representational change, if they have the right insight. Probably because of this, it is sometimes unclear whether the “Aha!” experience is associated with restructuring or with finding the solution. Note that once the problem solver gets into the impasse, representational change is necessary, but not sufficient for solving the problem: some problem solvers cannot solve the task even when they are told to relax the constraint (Weisberg and Alba, 1982 ; Kershaw et al., 2013 ). On the other hand, it is possible to solve insight tasks without going through impasse and insight, if the first search space is sufficient.

The cognitive level is the most interesting for us, but since it is hidden, we can only observe the behavioral and emotional correlates of cognitive processes. The affective level cannot be directly assessed, because we either have to rely on subjective reports of problem solvers about their feelings or we could measure correlates of their emotions (e.g., heart rate, galvanic skin response, piloerection, pupil dilation). The behavioral level can be described easily and objectively. Behavioral measures during insight problem solving usually involve the moves that problem solvers make in order to solve the task. The difficulty is to get enough data from participants and to convince them to act out their thoughts instead of trying to solve the problem in their heads.

Models: the order of problem solving stages

Wallas ( 1926 ) described the stages of insight problem solving as preparation, incubation, illumination, and verification. These roughly correspond to the stages described above. More recently, researchers constructed box-and-arrow type models, which show the possible sequences of problem solving stages (see Figures ​ Figures2, 2 , ​ ,3). 3 ). These models usually agree that the sequence of stages is different for people who solve the task with insight—who go through all the stages described above—from those who solve the task without insight; and that people who fail to solve the task get stuck in the impasse stage.

Beeftink et al.'s ( 2008 ) stage model of insight problem solving (modified figure) . Gray areas are part of impasse.

Öllinger et al. ( 2014b ) stage model of insight problem solving (original figure) .

For example, based on Beeftink et al.'s ( 2008 ) model (Figure ​ (Figure2), 2 ), the sequence of stages could be:

• Search → solve for people, who solve the task without impasse and insight,
• Search → fixation → search for people who can't solve the task, and
• Search → fixation → incubation → insight → solve for people who solve the task with restructuring.

In their model, fixation is an unconscious state, where people keep repeating previous problem solving attempts and incubation happens when the problem solver is in the conscious state of impasse: after unsuccessful attempts accumulate and reach a threshold, problem solvers realize that they are stuck and they take a break. Their model emphasizes the difference between routes with and without incubation: although it is possible that one cannot solve the task even after incubation, but it is not possible to solve the task without it.

Öllinger et al.'s ( 2014b ) model (Ohlsson, 1992 ; based on Jones, 2003 ) does not differentiate between fixation and incubation, but these are implicitly included in the impasse stage. Their model generates search → solution, and search → impasse → representational change → search → solution sequences (Figure ​ (Figure3 3 ).

Search space in the five-square problem

The search space of the Five-Square problem consists of the possible positions where the matchsticks could be placed (Simon and Newell, 1974 ). In our version of the task, this space was discretized: sticks could reside only on 180 predefined grid positions. The search space limits the number of possible stick movements, but it is probably still much larger than the actual search space of problem solvers—the collection of grid positions that they consider for a solution—because they rarely put sticks on the outer positions of the grid.

In a previous study, Öllinger et al. ( 2014a ) found that the self-imposed constraint in this task is to keep the original shape in one piece, so we hypothesized that participants would first only use grid positions close to the original shape. They would quickly exhaust this search space and start repeating previously explored grid positions with their stick movements. Problem solvers who overcome this constraint expand their search space. The behavioral correlate should be the selection of new grid positions—including those that are part of the solution—further away from the cross shape.

The present study

We propose an objective behavioral measure to define problem solving stages individually. We aimed to validate the stage models of insight by testing their predictions against this data. We were also interested how participants' subjective feelings correlate with their behavior.

We used the number of explored grid positions as a behavioral measure and tracked its changes through the problem solving attempts of participants. The grid positions explored by problem solvers are taken as instances from their cognitive search space and as such provide us with a window to their cognitive processes. Based on the stage model of insight, we predicted that in the case of problem solvers, who solve the task through restructuring, the number of explored grid positions would increase with every move at the beginning, until it reaches a plateau. The plateau indicates that the participant exhausted the possibilities within the constrained representation of the problem, and with every consecutive move the participant just repeats previous source and target positions. Participants could repeat positions even before exhausting the possibilities if they forget their previous moves. Some participants would give up, and stay inactive for longer periods of time. Both inactivity, and repetitions are taken as behavioral correlates of impasse (Beeftink et al., 2008 ), i.e., they can be used to objectively—independently of the problem solvers' feelings—identify the impasse stage. Some participants would get stuck in this stage, while others would get an insight and continue searching again. The search of an individual who had an insight is unconstrained by the idea that the shape should stay in one piece, so the person could put sticks further away from the original figure, and the number of explored grid positions would increase again until the person finds the solution. To sum up, we defined problem solving stages based on the curve of the number of explored grid positions through time for each participant individually and predicted that the sequence of problem solving stages would follow the process models of insight.

We also asked participants about their feelings related to insight and impasse. In our study, we used two self-reporting measures: an online impasse report and a post-hoc insight report. We asked participants in the impasse monitoring group to press a button when they felt being stuck during the task. After finishing the task, we asked all participants whether they had an “Aha!” experience (Danek et al., 2014 ). We predicted that more solvers would report insight than non-solvers, because successful solvers can have an “Aha!” experience, non-solvers probably cannot. We also predicted that non-solvers would report impasse more often than solvers, because all non-solvers should have an impasse, while solvers do not have it necessarily (it is possible to solve the task without impasse). We predicted that participants would report impasse during periods of frequent repetitions and inactivity, i.e., during the behaviorally defined impasse stage. According to Kounios and Beeman ( 2014 ) having an impasse is not necessary for having an “Aha!” experience—we wanted to see whether this claim holds for the five square problem too.

The task and design

In the Five-Square problem (Katona, 1940 ), the task is to reduce the number of five squares seen on Figure ​ Figure1 1 to four squares. Participants should move three sticks to new grid positions without discarding any sticks (see solution in the Supplementary Material, Data Sheet 2 ).

We introduced two experimental groups. In the impasse monitoring group participants were provided with a description of the impasse feeling before they started the task, and they were asked to press a button when they felt like that during the task. A second group served as a control group to see whether the metacognitive task of monitoring one's impasse state had an impact on problem solving success.

Participants

Recruitment.

Four participants were recruited at Queen Mary University, London; the rest of the participants were recruited on the Internet, via a crowdsourcing platform called CrowdFlower. Here, people willing to work online can sign up and then choose from the available jobs that employers offer. We recruited “level 3 workers,” who are the highest rated, most trustworthy group of workers on CrowdFlower. They received one dollar as a payment. The participants were randomly assigned to either the impasse monitoring group or the control group.

Our experiments obey the Declaration of Helsinki (2013). We followed the code and the ethical principles of the German Psychological Society and the European Commission. Participants were allowed to quit the online experiment any time without providing a reason.

Sample size

We had more than twice as many participants in the impasse monitoring group than in the control group because we wanted to analyse the impasse monitoring group in more detail, namely perform a paired t -test on those participants who pressed the impasse button. We computed the required sample size for this test a priori with the G * Power software (Faul et al., 2007 ), assuming a medium effect size (0.5) and setting α = 0.05 and power = 0.8. According to the analysis, the sample size for a matched-pairs t -test with these parameters should be 34, which we multiplied by 2.5 thinking that about half of the participants won't be able to solve the task and not all of these will press the impasse button. At the end, this analysis proved to be insufficient, since we assumed normal distribution, but the data was not normally distributed, so we had to do a non-parametric test instead of the planned paired t -test.

Exclusion criteria

We excluded all participants who closed the software before either they solved the task or the 15 min elapsed, even if they restarted the software afterwards. We did this, because we could not monitor their behavior while the program was closed.

Demographics

After excluding participants who closed the software early, 129 participants remained; 42 in the control group and 87 in the impasse monitoring group. There were 27 females and 102 males. The average age of participants was 30.3 years (range 16–69). We had participants from 37 countries and five continents (Europe = 59, Asia = 44, North-America = 9, South-America = 12, Africa = 5). The solvers and non-solvers were almost equally distributed across continents. Only four countries had more than five participants (India: 20, USA: 9, Romania: 7, UK: 6). Most of our participants had some higher education. Eleven participants had basic levels of English, the rest judged their English as intermediate level or higher.

Materials and procedures

We provided a downloadable version of the Five-Square problem, written in Microsoft Visual Basic®, on the Internet. The program was run individually on the participants' computers and guided them through the experiment autonomously.

The program started with a practice trial, where participants had to drag and drop four sticks on the screen to four different grid positions. After completing this task participants received the following written instruction:

“ You will see five squares made of sticks on the screen. Your task is to move exactly three sticks to produce four squares of equal size, while leaving no sticks that are not part of squares . After three moves the task resets automatically or you can reset it anytime by pressing the Reset button. You can try to solve the task as many times as you like, in fact, try to show us all your ideas by moving the sticks, don't just try to solve the task in your head. You will have 15 min to solve the task—try to use all of it. It is not a problem, if you cannot solve the task, but if you close the program before 15 min elapsed, your submission will be invalid.”

Participants in the impasse-monitoring group received an additional instruction:

“ Sometimes before solving a difficult problem people feel like they are stuck, they are not getting closer to the solution. We would like to know if you feel like this during the task, so in this case please press the ‘I’m stuck' button. You can press the button more than once if you feel that this feeling increases.”

After receiving the instructions, the initial figure of five squares appeared on the screen and participants could move the sticks by drag-and-drop with the mouse. The program recorded the movement of the sticks and the button presses (Impasse button and Restart button) along with the time that passed since starting the task. It has automatically checked whether a correct solution was achieved.

Participants were allowed to restart from the initial configuration of sticks as often as they wanted by pressing the “Restart” button. Alternatively, the program reset automatically after unsuccessful attempts of three moves and provided feedback (“ This is not a correct solution. Please, try again! ”). After solving the problem or reaching the upper time limit of 15 min, participants were asked to post the output log file to the experimenter via our website and to complete a short online questionnaire (about their age, gender, handedness, vision, educational background, nationality, mother tongue, and level of English). All participants were asked whether they solved the problem with or without insight:

“ Some people feel a sudden, unexpected, unintended, and surprising moment where a solution pops into someone's mind. The accompanying experience is often called ‘Aha!’ experience. Did you have this feeling before or when you solved the task?”

The participants had to choose between the following answers: I did not solve the task; No, I did not feel anything like this; Yes, I felt exactly like this; Other: [free text].

Analyses of problem solving stages

We plotted the number of explored grid positions vs. time for each participant individually (see Figures ​ Figures4, 4 , 6 and the Supplementary Material). On these plots, each point represents a move (dragging-and-dropping one stick). The number of explored grid positions includes the source positions (where the stick was picked up from) and the target positions (where the stick was put down to). With each move, it either increases by two (if the move consisted of new source and target positions), increases by one (if either the source position or the target position is a position that has already been used—i.e., if the move involves a repetition of a grid position), or stays constant (if both the source and the target position are repetitions).

The number of explored grid positions vs. time, cartoon figure with made up data . This is what we expected the performance of a typical solver would look like. Each data point on these plots represents a stick movement. Slopes, plateaus, and gaps (see definitions in the Methods section) are identified and demarcated by black vertical lines.

For the purposes of our analyses, we defined three different patterns on these plots:

• A slope consists of minimum three consecutive moves that continuously increase the number of explored grid positions. This means that each move within the slope includes at least one new grid position that the participant has not used before.
• A plateau consists of minimum three consecutive moves that do not increase the number of explored grid positions. Moves within the plateau consist of repetitions of previously used grid positions.
• A gap is a period of time between two moves if it is longer than the average time between two consecutive moves for the participant + 2 * SD. In case of first moves of trials, the time between the move and the last move of the previous trial includes the time spent by restarting the task, because the figure was visible during restarting.

On the behavioral level, these patterns translate to search, repetition and inactivity , respectively, which we hypothesize to indicate the cognitive phases of search (slope) and impasse (plateau or gap). We identified slopes, plateaus and gaps in the plots of each participant and looked at whether they conformed to the sequence of problem solving stages generated by the box-and-arrow models of insight problem solving. Figure ​ Figure4 4 shows a made up example: it summarizes our predictions about the behavior of a typical solver conforming to current models of insight problem solving.

Effect of manipulation

To control whether the additional metacognitive task in the impasse monitoring group affected problem solving performance, we compared the two groups in terms of solution rate and solution time.

Solution rate

The overall solution rate was 51%; 55% in the control group and 49% in the impasse monitoring group (Table ​ (Table2). 2 ). According to the Chi-square test, the difference was not significant: χ 2 (1, N = 129) = 0.14, p = 0.70, Φ = 0.03.

Solution rate in the two experimental groups .

Solution time

Twenty nine participants solved the task under 1 min in the two groups. The rest of the solution times were more or less evenly distributed between 2 and 15 min. We compared the solution time of solvers in the control group and the impasse monitoring group with a Mann-Whitney U -test—the difference between the groups was not significant, U = 424.00, p = 0.34, r = 0.12. For non-solvers, the task always ended after 15 min in both groups.

Since we did not find differences between the groups, we merged them for the rest of the analyses, except when we looked at the impasse monitoring group separately for the subjective impasse feeling analysis.

Exclusion criteria for data analysis

There were 28 participants who only had one trial. Twenty six of these solved the task under 32 s; one solved it in 3.4 min and another one did not solve it. It is probable that the former solved the task in his head and the latter gave up after only one trial, and those 26 participants, who solved it in about half minute either already knew the task or just found the solution instantly. We excluded these 28 participants from the rest of the analyses, because we do not have enough movement data from them and also because we suspect that they knew the solution in advance.

One hundred and one participants remained, 34 in the control group (15 solvers) and 67 in the impasse monitoring group (24 solvers). The overall solution rate decreased to 39%.

Target positions

To illustrate how the actual search space of participants changed over time we plotted the grid with hues proportional to the relative frequency of positions used as targets (Figure ​ (Figure5)—for 5 )—for calculating the relative frequencies we used the first half of moves of each participant for the plot on the left and the second half of moves of each participant for the plot on the right.

The frequency of grid positions used as target positions in the moves of solvers in the first quarter of their moves (left) and the last quarter of their moves (right) . The shades of grid positions represent a heat map: the darker the shade, the more frequently the position was chosen. Invisible positions were not used at all.

We can see that the most frequent positions were the ones closest to the original cross shape (those that complemented the cross shape to a three-by-three square); the frequency of these eight positions (drawn in black in Figure ​ Figure5 5 because they had the highest frequency) decreased over time: M = 51.4, SD = 3.6 in the first half of moves, and M = 38.4, SD = 9.9 in the second half of moves, t (7) = 3.6, p = 0.009, d = 2.7032. On the other hand, the frequency of those 12 positions that could be part of the solution increased over time: M = 9.8, SD = 3.9 in the first half of moves, and M = 19.9, SD = 3.6 in the second half of moves, t (11) = 9.6, p < 0.0001, d = 5.8029.

Repetition rate

We compared the proportion of repeated positions of solvers and non-solvers. According to the unpaired t -test, the repetition rate of non-solvers ( M = 0.5, SD = 0.2) was significantly higher than that of solvers ( M = 0.3, SD = 0.3), t (99) = 5.13, p < 0.0001, d = 1.03.

Problem solving stages

We looked at the number of explored grid positions through time for each participant (see the figures in the Supplementary Material and four examples in Figure ​ Figure6) 6 ) and we identified slopes, plateaus, and gaps, as defined in the Methods section. There were uncategorized moves that did not fall into neither slopes, nor plateaus—for the sake of simplicity, we ignored these. For 11 solvers and 6 non-solvers there was a gap before the first move—we disregarded these gaps too, because probably these were not signs of impasse.

The number of explored grid positions vs. time . This figure shows data from four participants (two solvers, two non-solvers). The plots of all the participants can be found in the Supplementary Data. Examples plotted in green (#18 and #4) are from solvers, examples plotted in red (#79 and #7) are from non-solvers. Examples #18 and #79 conform to the stage model of insight, whereas examples #4 and #7 reveal more complex sequences of problem solving stages. Each data point on these plots represents a stick movement. Slopes, plateaus, and gaps (see definitions in the Methods section) are highlighted with different shades of gray: slopes are dark gray, plateaus are medium, and gaps are light gray. Asterisks on the horizontal axis indicate the time of impasse button presses in case of participant #79 (the rest of the participants in this figure were in the control group).

All participants had at least one slope. The gap was missing in case of 5 solvers and 1 non-solver and the plateau was missing in case of 16 solvers and 5 non-solvers. Table ​ Table3 3 shows the different sequences, their interpretation and the number of participants who had such a sequence. We categorized the sequences based on whether they conformed to the stage model of insight problem solving.

Sequences of problem solving stages, their interpretation and the number of participants who had such a sequence .

The last column on the right summarizes how many solvers and non-solvers conformed (gray background) or did not conform (white background) to the stage model of insight .

We have found that 49% (19 out of 39) of the solvers and 13% (8 out of 62) of the non-solvers followed the classic stage model of insight. The rest of the participants had more complex sequences, with search and impasse stages recurring several times.

Subjective feelings of insight and impasse

Subjective insight, impasse, and success.

In the two groups, 74% of the solvers (29 participants out of 39 solvers) and 10% of the non-solvers (6 participants out of 62 non-solvers) reported insight feeling after the task. According to the Chi-square test with Yates correction, the association between having an insight and being a solver was significant, χ 2 (1, N = 101) = 41.42, p < 0.0001, Φ = 0.64.

In the impasse monitoring group 33% of the solvers (8 participants out of 24 solvers) and 79% of the non-solvers (34 participants out of 43 non-solvers) pressed the impasse button at least once. According to the Chi-square test with Yates correction, the association between pressing the impasse button and being a non-solver was significant,χ 2 (1, N = 67) = 11.89, p < 0.0006, Φ = 0.42.

Temporal distribution of impasse button presses

We tested whether participants in the impasse monitoring group tended to press the impasse button during plateaus and gaps or during slopes. There were 42 participants who pressed the button at least once—only these participants were included in the following two analyses.

We calculated the number of impasse button presses per minute during plateaus and gaps together and during slopes. According to the Wilcoxon matched-pairs signed-ranks test, the medians did not differ significantly, Z = 0.63, p = 0.53, r = 0.10.

This is quite unexpected so we checked whether non-solvers tended to press the impasse button more often during the second half of the task (7.5–15 min) than during the first half of the task (0–7.5 min). According to the paired t -test, the difference was not significant, t (33) = 0.46, p = 0.65, d = 0.16.

Association of plateaus and gaps with reported “Aha!” experience

We compared the length of plateaus and gaps of solvers, who reported insight and solvers, who did not report insight. According to the unpaired t -test the difference was not significant, t (37) = 1.04, p = 0.31, d = 0.3403. In fact, there were three solvers, who reported insight and did not have any plateaus or gaps, just a short slope.

Discussion and conclusions

Summary of results.

We investigated problem solving stages in the Five-Square problem based on the main assumptions of the restructuring hypothesis of insight, i.e., that problem solving proceeds in different stages, including conscious search, impasse, and restructuring. We used a behavioral measure, the time and trajectory of stick movements by participants, to objectively define problem solving stages. This was based on the assumptions that during search the problem solver explores new grid positions, while during impasse, the problem solver either repeats previously explored grid positions or stays inactive. We analyzed how these stages follow each other and how they correlate with subjective impasse and insight feelings of the participants.

We have found that less than half of the successful problem solvers, and 13% of the unsuccessful participants followed the sequence of problem solving stages that the stage models of insight predicted. The rest of the participants had more complicated sequences of search and impasse, with these stages alternating several times. This means that the stage models must be extended to explain variability on the individual level. Most of this variability disappears in group-level analysis, which highlights the importance of individual analysis of problem solving behavior.

Solvers reported insight feeling more often than non-solvers and non-solvers reported impasse feeling more often than solvers, as it was expected. We predicted that the behaviorally defined impasse would correlate with the subjective feelings of participants, but we did not find temporal correlation between objective impasse stages and subjective impasse reports. This shows that impasse reports might be unreliable indicators of impasse.

Empirical validation of problem solving stages

Although it has long been proposed that the process of insight problem solving can be divided into stages (Ohlsson, 1992 ; Sandkühler and Bhattacharya, 2008 ), there were very few studies that tried to empirically validate this hypothesis.

Knoblich et al. ( 2001 ) asked participants to solve matchstick arithmetic tasks while recording their eye-movements. They divided the problem solving time of each participant in three equally long intervals and compared mean fixation durations across intervals. They found that mean fixation duration increased across intervals on average, which they took as a sign that more and more participants entered impasse with time. This finding is based on the assumption that impasse is associated with longer fixations, because people tend to stare blankly at the screen when they don't know what to do. They also found that people tend to fixate on different elements of the task in each interval: in the first interval their attention is differentially allocated on elements that are consistent with the constrained search space induced by prior knowledge, while in the second and third intervals successful solvers look more at the elements of the extended search space. These findings seem to support the search-impasse sequence predicted by stage models of insight, however, the results were based on group level analyses, which mask individual variation.

Jones ( 2003 ) criticized that Knoblich et al. ( 2001 ) determined problem solving stages post-hoc . He examined move durations and eye-movements during two versions of the car park problem. He defined impasse as a longer break before the critical (insightful) move, i.e., in his definition, impasse is a time interval between two moves. This longer thinking time before the critical move also coincided with longer fixation times. In Jones's study there is only one impasse per definition, moreover, he also assumed that participants did not make moves during impasse, which we find problematic.

Fleck and Weisberg ( 2013 ) analyzed insight problem solving by thinking-aloud protocols (Ericsson and Simon, 1993 ). They found only weak evidence for the “classic impasse-restructuring-insight sequence” (p. 436), instead, participants used a variety of strategies. E.g., some participants solved the problem by using prior knowledge that they gathered from the solution of similar problems. Other participants solved the problem by the application of heuristics that helped them to restrict the search space. At last, some participants restructured their problem representation after they failed several times. Only these participants supposedly went through the problem solving stages described by the restructuring hypothesis.

A new model for insight problem solving

Our main finding—that in most cases problem solving stages do not follow the simple stage model of insight—highlights the need for revising the model. The model should be able to explain recurring search and insight stages. There are different versions of the model, but all include search, impasse and restructuring/insight, but none of them can generate the variety of the sequences of these stages that we found. For example, Beeftink et al.'s ( 2008 ) model could be extended with loops to be able to account for various problem solving types. Their model already includes the possibility to go back to search behavior (“work on a problem”) once more after the impasse (Start working on a problem → Problem progress → Fixation → Continue to work on problem), but it does not allow to go back more than once or to go back and forth between fixation (repetitions) and incubation (inactivity). Öllinger et al.'s ( 2014b ) model could also be modified to allow for a more flexible sequence of stages by making the arrow between search and impasse double headed.

We provide our own version of the model in Figure ​ Figure7. 7 . It emphasizes that both before restructuring and after restructuring search, repetitions, and inactivity could follow each other in any order: each stage is accessible from the other two stages. Our model clearly separates the behavioral and the cognitive level, emphasizing the difference between objective observations and theory.

Box-and-arrow model of insight problem solving . White circles include problem solving stages described on the behavioral level. Gray shading refers to the cognitive level. Repetition and inactivity are sub-stages of impasse. Problem solving can either start in the restricted search space and then continue in the extended search space after restructuring, or could start in the extended search space right away.

Box-and-arrow type stage models explain the order of problem solving stages, and the underlying theory of representational change explains—to some extent—what drives the process through these stages. Repetitions and inactivity on the cognitive level are supposedly caused by the confined search space: when there is a finite number of candidate solutions, after trying enough of them, the problem solver inevitably bumps into repeating previous ones, unless the problem solver takes a break. We found that non-solvers have a higher repetition rate than solvers which could be the result of either a smaller search space, more time spent in impasse or poorer working memory. Restructuring leads to an extended search space, which includes more candidate solutions and among them, the solution, and thus repetitions and inactivity is less frequent than in the restricted search space.

Limitations

Impasse button presses.

There has been a long tradition of identifying different problem solving stages by self-reports or thinking aloud protocols (Duncker and Lees, 1945 ; Schooler et al., 1993 ; Jung-Beeman et al., 2004 ; Danek et al., 2013 ; Fleck and Weisberg, 2013 ), but most often, self-reports about the “Aha!” experience are used only to differentiate between insight and non-insight solutions (Jung-Beeman et al., 2004 ). To our knowledge, there were no studies so far that tried to find an association between the time of impasse reports and some other, objectively defined impasse stage.

We did not find a temporal correlation between the objectively defined impasse and the impasse reports of participants. There are several possibilities why this happened so. The link between the objectively defined impasse stage and the impasse reports of participants has several elements: the cognitive impasse state causes repetitions and inactivity on the behavioral level that we used to objectively define impasse. The same cognitive state might cause the subjective feeling of being stuck which should remind the participant to press the impasse button.

It is possible that the subjective feelings of participants do not correlate with their cognitive state of impasse, i.e., they are not aware that they are in an impasse. Another possibility is that the subjective feeling does not correlate with the button presses: either because our instructions were unclear about the impasse, or because subjects left the computer during some of the gaps and thus were not in the position to press the button.

Of course, it is also possible that repetition and inactivity are not reliable signals of impasse or that the definitions we used to operationalize them were ineffective. In the literature impasse has a double definition: on the one hand it is defined behaviorally as repetitions and/or inactivity (Knoblich et al., 2001 ; Jones, 2003 ; Beeftink et al., 2008 ); on the other hand it is defined as a feeling of being stuck (Ohlsson, 1992 ). We believe that it is better to start with the objective behavioral definition than with the subjective definition based on feelings. In our data, subjective impasse reports are equally likely to occur at the beginning, middle or end of the problem solving time—they do not show any obvious pattern or aggregation. The other problem is that they are quite infrequent so it would be hard to define stages based on them. But most importantly, we believe that stick movements are better reflections of the cognitive processes going on in the problem solver's mind than his feelings, let alone button presses supposedly based on his feelings. Monitoring one's feelings is a parallel task, besides the main task of problem solving and the problem solver most likely concentrates more on solving the task than analysing and reporting his feelings.

We should also explain the counter-intuitive finding that 6 of the non-solvers reported having an “Aha!” experience. There could be several reasons for that. It is possible that participants did not understand our instructions properly, or that these participants had a kind of partial or wrong insight (Öllinger and Knoblich, 2009 ). It is also possible that the “Aha!” experience is not linked to representational change (Danek et al., 2014 ).

Online task

Our overall solution rate was a bit higher than expected (54%), but more importantly, we had several participants who solved the task very quickly. This could raise suspicion about the reliability of the online task: after all, without supervision from the experimenter, participants could look up the solution of the task online, or they could seek help from someone else. To decrease this possibility, we excluded participants who solved the task in one trial and kept only those who generated more data. The solution rate after the exclusion was 39%, which is comparable to previous studies (Öllinger et al., 2014a ).

No supervision also meant that participants could act more freely, and that they were in a familiar setting (probably their homes), which allowed them to take a break whenever they wanted. In laboratory experiments participants probably feel pressure from the experimenter to move sticks at a constant pace, which could result in loosing inactivity as a measure of impasse in a laboratory setting.

Using an online crowdsourcing platform, such as CrowdFlower also helped us to recruit participants with a variety of backgrounds. Research in cognitive psychology suffers from the homogeneity of participant populations: between 2003 and 2007, about 80% of participants in psychological experiments were undergraduate students (Henrich et al., 2010 ). This WEIRD population (Western Educated Industrialized Rich Democratic) might be the least representative for all of humanity, and in some areas it might even be the outlier (Henrich et al., 2010 ). Our methods represent one step toward involving participants of different ages, nationalities, and with different educational backgrounds, enabling us to draw more general conclusions about humans.

Definition of problem solving stages

There seems to be a consensus in the literature that inactivity and repetitions are behavioral correlates of impasse, and that during the search stage the problem solver makes new moves, so we used gaps, plateaus and slopes as the behavioral signals of different stages of problem solving. Our definitions of slope and plateau are arbitrary to some extent: we set three moves as the minimum length of these stages. Setting them shorter would have made the sequence of stages intractable, while setting them longer would have resulted in ignoring too many transient moves. For gaps, we used the most common outlier criterion, i.e., longer than the average move time plus two SDs. Here, the balance is also between identifying too many or too few gaps.

As can be seen in Figure ​ Figure1, 1 , the initial configuration of sticks was symmetric. Consequently, there were four different sites where a solution could occur and the symmetric moves were equivalent. For our analyses, we decided not to take into consideration the symmetry of the figure and when we counted the number of explored grid positions, we did not collapse equivalent positions into the same category. We did this, because it turned out that participants did not use all segments of the figure equivalently: the top left portion was used less often than the rest.

Future research

Future research should include adapting our methods of defining problem solving stages in other insight problems. The nine dot problem seems to be a good candidate, because it is also a multistep problem with a discretized search space where participants make relatively many moves.

Another interesting direction would be to try to find the neural correlates of problem solving stages and thus to add the neural level of description to the narrative. So far, most brain imaging studies tried to find the neural correlates of insight (Dietrich and Kanso, 2010 ; Dietrich and Haider, 2014 ; Kounios and Beeman, 2014 ), but now that we can pinpoint the beginning and the end of all problem solving stages we could look at the difference between brain activity during all the different stages of problem solving.

The restructuring hypothesis does not explain the process that generates the candidate hypotheses during conscious search and the process that leads to restructuring. Bayesian models explain how hypotheses (candidate solutions) are selected but most of them take the initial population of hypotheses as a given, except some notable exceptions (Kemp and Tenenbaum, 2008 ). A process generating candidate hypotheses seems to be a must. A question is how a mental search in the hypothesis space is conducted. It remains to be seen whether an evolutionary search (as in Darwinian neurodynamics, Fernando et al., 2012 ) could ultimately explain the observations; this we shall consider in a subsequent paper.

To sum up, we pioneered a new method for finding problem solving stages in the five square problem based on solely behavioral data. The analysis of problem solving stages revealed a discrepancy between existing stage models of insight problem solving and our data, which highlights the need for revising the models and to further investigate problem solving stages on the individual level.

Conflict of interest statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The research leading to these results has received funding from the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement no 308943 (INSIGHTproject) and by the European Research Council's Advanced Grant under grant agreement no 294332 (EvoEvo project).

Supplementary material

The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fpsyg.2015.01050

Presentation 1.zip: Figures for all the participants like the ones shown in Figure 6 (The number of explored grid positions vs. time).

Presentation 2.zip: Animation of participants' stick movements. The videos show the moves in order, one move per second - the time of moves is not shown, because it would make the videos too long to watch.

Data Sheet 1.xlsx: Raw data file. This file contains all data that we collected from participants during problem solving and through the questionnaires.

Data Sheet 2.PDF: A possible solution of the task (three other rotations are also possible).

• Beeftink F., van Eerde W., Rutte C. G. (2008). The effect of interruptions and breaks on insight and impasses: do you need a break right now? Creat. Res. J . 20 , 358–364. 10.1080/10400410802391314 [ CrossRef ] [ Google Scholar ]
• Boden M. (2004). The Creative Mind: Myths and Mechanisms . New York, NY: Basic Books. [ Google Scholar ]
• Bowden E., Beeman M. (1998). Getting the right idea: semantic activation in the right hemisphere may help solve insight problems . Psychol. Sci. 9 , 435–440. 10.1111/1467-9280.00082 [ CrossRef ] [ Google Scholar ]
• Bowden E. M., Jung-Beeman M., Fleck J., Kounios J. (2005). New approaches to demystifying insight . Trends Cogn. Sci. 9 , 322–328. 10.1016/j.tics.2005.05.012 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Bowers K., Regehr G., Balthazard C., Parker K. (1990). Intuition in the context of discovery . Cogn. Psychol. 22 , 72–110. 10.1016/0010-0285(90)90004-N [ CrossRef ] [ Google Scholar ]
• Danek A., Fraps T., von Mueller A. (2014). Working wonders? Investigating insight with magic tricks . Cognition 130 , 174–185. 10.1016/j.cognition.2013.11.003 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Danek A., Fraps T., von Müller A. (2013). Aha! experiences leave a mark: facilitated recall of insight solutions . Psychol. Res. 77 , 659–669. 10.1007/s00426-012-0454-8 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Dietrich A., Haider H. (2014). Human creativity, evolutionary algorithms, and predictive representations: the mechanics of thought trials . Psychon. Bull. Rev . [Epub ahead of print]. 10.3758/s13423-014-0743-x [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Dietrich A., Kanso R. (2010). A review of EEG, ERP, and neuroimaging studies of creativity and insight . Psychol. Bull. 136 , 822–848. 10.1037/a0019749 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Duncker K., Lees L. (1945). On problem-solving . Psychol. Monogr. 58 , i–113. 10.1037/h0093599 [ CrossRef ] [ Google Scholar ]
• Durso F. T. F., Rea C. C. B., Dayton T. (1994). Graph-theoretic confirmation of restructuring during insight . Psychol. Sci. 5 , 94–97. 10.1111/j.1467-9280.1994.tb00637.x [ CrossRef ] [ Google Scholar ]
• Ericsson K., Simon H. (1993). Protocol Analysis: Verbal Reports as Data, Revised Edn . Cambridge, MA: The MIT Press. [ Google Scholar ]
• Faul F., Erdfelder E., Lang A., Buchner A. (2007). G * Power 3: a flexible statistical power analysis program for the social, behavioral, and biomedical sciences . Behav. Res. Methods 39 , 175–191. 10.3758/BF03193146 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Fernando C., Goldstein R., Szathmáry E. (2010). The neuronal replicator hypothesis . Neural Comput. 22 , 2809–2857. 10.1162/NECO_a_00031 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Fernando C., Szathmáry E., Husbands P. (2012). Selectionist and evolutionary approaches to brain function: a critical appraisal . Front. Comp. Neurosci. 6 : 24 . 10.3389/fncom.2012.00024 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Fleck J., Weisberg R. (2013). Insight versus analysis: evidence for diverse methods in problem solving . J. Cogn. Psychol. 25 , 436–463. 10.1080/20445911.2013.779248 [ CrossRef ] [ Google Scholar ]
• Henrich J., Heine S. J., Norenzayan A. (2010). The weirdest people in the world? Behav. Brain Sci. 33 , 61–83; discussion: 83–135. 10.1017/S0140525X0999152X [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Jones G. (2003). Testing two cognitive theories of insight . J. Exp. Psychol. 29 , 1017–1027. 10.1037/0278-7393.29.5.1017 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Jung-Beeman M., Bowden E. M., Haberman J., Frymiare J. L., Arambel-Liu S., Greenblatt R., et al.. (2004). Neural activity when people solve verbal problems with insight . PLoS Biol. 2 :97. 10.1371/journal.pbio.0020097 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Katona G. (1940). Organizing and Memorizing: Studies in the Psychology of Learning and Teaching . New York, NY: Columbia University. [ Google Scholar ]
• Kemp C., Tenenbaum J. B. (2008). The discovery of structural form . Proc. Natl. Acad. Sci. U.S.A. 105 , 10687–10692. 10.1073/pnas.0802631105 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Kershaw T., Flynn C., Gordon L. (2013). Multiple paths to transfer and constraint relaxation in insight problem solving . Think. Reas. 19 , 96–136. 10.1080/13546783.2012.742852 [ CrossRef ] [ Google Scholar ]
• Knoblich G., Ohlsson S., Haider H., Rhenius D. (1999). Constraint relaxation and chunk decomposition in insight problem solving . J. Exp. Psychol. 25 , 1534–1555. 10.1037/0278-7393.25.6.1534 [ CrossRef ] [ Google Scholar ]
• Knoblich G., Ohlsson S., Raney G. (2001). An eye movement study of insight problem solving . Mem. Cogn. 29 , 1000–1009. 10.3758/BF03195762 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Kounios J., Beeman M. (2014). The cognitive neuroscience of insight . Ann. Rev. Psychol. 65 , 71–93. 10.1146/annurev-psych-010213-115154 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Kounios J., Frymiare J. L., Bowden E. M., Fleck J. I., Subramaniam K., Parrish T. B., et al.. (2006). The prepared mind. Neural activity prior to problem presentation predicts subsequent solution by sudden insight . Psychol. Sci. 17 , 882–890. 10.1111/j.1467-9280.2006.01798.x [ PubMed ] [ CrossRef ] [ Google Scholar ]
• MacGregor J. N., Ormerod T. C., Chronicle E. P. (2001). Information processing and insight: a process model of performance on the nine-dot and related problems . J. Exp. Psychol. 27 , 176–201. 10.1037/0278-7393.27.1.176 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Metcalfe J., Wiebe D. (1987). Intuition in insight and noninsight problem solving . Mem. Cogn. 15 , 238–246. 10.3758/BF03197722 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Öllinger M., Jones G., Knoblich G. (2014a). Insight and search in Katona's Five-Square problem . Exp. Psychol. 61 , 263–272. 10.1027/1618-3169/a000245 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Öllinger M., Jones G., Knoblich G. (2014b). The dynamics of search, impasse, and representational change provide a coherent explanation of difficulty in the nine-dot problem . Psychol. Res. 78 , 266–275. 10.1007/s00426-013-0494-8 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Öllinger M., Knoblich G. (2009). Psychological research on insight problem solving, in Recasting Reality: Wolfgang Pauli's Philosophical Ideas and Contemporary Science , eds Atmanspacher H., Primas H. (Berlin-Heidelberg: Springer; ), 275–300. [ Google Scholar ]
• Ohlsson S. (1984a). Restructuring revisited: I. Summary and critique of the Gestalt theory of problem solving . Scand. J. Psychol. 25 , 65–78. 10.1111/j.1467-9450.1984.tb01001.x [ CrossRef ] [ Google Scholar ]
• Ohlsson S. (1984b). Restructuring revisited: II. An information processing theory of restructuring and insight . Scand. J. Psychol. 25 , 117–129. 10.1111/j.1467-9450.1984.tb01005.x [ CrossRef ] [ Google Scholar ]
• Ohlsson S. (1992). Information-processing explanations of insight and related phenomena, in Advances in the Psychology of Thinking , eds Keane M., Gilhooly K. (London: Harvester-Wheatsheaf; ), 1–44. [ Google Scholar ]
• Sandkühler S., Bhattacharya J. (2008). Deconstructing insight: EEG correlates of insightful problem solving . PLoS ONE 3 :1459. 10.1371/journal.pone.0001459 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Schooler J., Ohlsson S., Brooks K. (1993). Thoughts beyond words: when language overshadows insight . J. Exp. Psychol. 122 , 166–183. 10.1037/0096-3445.122.2.166 [ CrossRef ] [ Google Scholar ]
• Seifert C., Meyer D., Davidson N., Patalano A., Yaniv I. (1994). Demystification of cognitive insight: opportunistic assimilation and the prepared-mind hypothesis, in The Nature of Insight , eds Sternberg R. J., Davidson J. E. (Cambridge, MA: MIT Press; ), 65–124. [ Google Scholar ]
• Simon H., Newell A. (1974). Thinking processes, in Contemporary Developments in Mathematical Psychology , Vol. 1 , eds Krantz D. H., Atkinson R. C., Luce R. D., Suppes P. (San Francisco, CA: W.H. Freeman; ), 101–104. [ Google Scholar ]
• Wallas G. (1926). The Art of Thought . New York, NY:Harcourt Brace Jovanovich. [ Google Scholar ]
• Wegner D. (2002). The Illusion of Conscious Will . Cambridge, MA: MIT Press. [ Google Scholar ]
• Weisberg R., Alba J. (1982). Problem solving is not like perception: more on Gestalt theory . J. Exp. Psychol. 111 , 326–330. 10.1037/0096-3445.111.3.326 [ CrossRef ] [ Google Scholar ]
• Wertheimer M. (1959). Productive Thinking . New York, NY: Harper. [ Google Scholar ]

Self-Esteem

It’s ok you can’t solve every problem, trying to “fix" everything can leave you feeling like a failure..

Updated May 10, 2024 | Reviewed by Ray Parker

• What Is Self-Esteem?
• Find counselling near me
• Your intrinsic value is more than what you can do for other people.

You are still worthwhile and can be successful, even if you don’t have all the solutions.

• Consider which decision will make you feel you’ve stayed true to your values.

In coaching others, I often discuss problem-solving strategies to help individuals think creatively and consider many options when they are faced with challenging situations.

Problem solving 1-2 includes the following:

• Define the problem, identify obstacles, and set realistic goals .
• Generate a variety of alternative solutions to overcome obstacles identified.
• Choose which idea has the highest likelihood to achieve the goal.
• Try out the solution in real-life and see if it worked or not.

Problem-solving strategies can be helpful in many situations. Thinking creatively and testing out different potential solutions can help you come up with alternative ways of solving your problems.

While many problems can be solved, there are also situations in which there is no “perfect” solution or in which what seems to be the best solution still leaves you feeling unsatisfied or like you’re not doing enough.

I encourage you to increase your comfort around the following three truths:

1. You can’t always solve everyone else’s problems.

2. You can’t always solve all of your own problems.

3. You are not a failure if you can’t solve every problem.

You can’t always solve everyone else’s problems.

When someone around you needs help, do you feel compelled to find solutions to their problem?

Are you seen as the problem solver at your job or in your close relationships?

Does it feel uncomfortable for you to listen to someone tell you about a problem and not offer solutions?

There are times when others come to you because they know you can help them solve a problem. There are also times when the other person is coming to you not for a solution to their problem, but for support, empathy, and a listening ear.

Your relationships may be negatively impacted if others feel that you don’t fully listen and only try to “fix” everything for them. While this may feel like a noble act, it may lead the other person to feel like they have failed or that you think they are unable to solve their own problems.

Consider approaching such situations with curiosity by saying to the other person:

• As you share this information with me, tell me how I can best support you.
• What would be most helpful right now? Are you looking for an empathetic ear or want to brainstorm potential next steps?
• I want to be sure I am as helpful as I can be right now; what are you hoping to get out of our conversation?

You can’t always solve all of your own problems.

We are taught from a young age that problems have a solution. For example, while solving word problems in math class may not have been your favorite thing to do, you knew there was ultimately a “right” answer. Many times, the real world is much more complex, and many of the problems that you face do not have clear or “right” answers.

You may often be faced with finding solutions that do the most good for the most amount of people, but you know that others may still be left out or feel unsatisfied with the result.

Your beliefs about yourself, other people, and the world can sometimes help you make decisions in such circumstances. You may ask for help from others. Some may consider their faith or spirituality for guidance. While others may consider philosophical theories.

Knowing that there often isn’t a “perfect” solution, you may consider asking yourself some of the following questions:

• What’s the healthiest decision I can make? The healthiest decision for yourself and for those who will be impacted.
• Imagine yourself 10 years in the future, looking back on the situation: What do you think the future-you would encourage you to do?
• What would a wise person do?
• What decision will allow you to feel like you’ve stayed true to your values?

You are not a failure if you can’t solve all of the problems.

If you have internalized feeling like you need to be able to solve every problem that comes across your path, you may feel like a failure each time you don’t.

It’s impossible to solve every problem.

Your intrinsic value is more than what you can do for other people. You have value because you are you.

Consider creating more realistic and adaptive thoughts around your ability to help others and solve problems.

Some examples include:

• I am capable, even without solving all of the problems.
• I am worthwhile, even if I’m not perfect.
• What I do for others does not define my worth.
• In living my values, I know I’ve done my best.

I hope you utilize the information above to consider how you can coach yourself the next time you:

• Start to solve someone else’s problem without being asked.
• Feel stuck in deciding the best next steps.
• Judge yourself negatively.

1. D'zurilla, T. J., & Goldfried, M. R. (1971). Problem solving and behavior modification. Journal of abnormal psychology, 78(1), 107.

2. D’Zurilla, T. J., & Nezu, A. M. (2010). Problem-solving therapy. Handbook of cognitive-behavioral therapies, 3(1), 197-225.

Julie Radico, Psy.D. ABPP, is a board-certified clinical psychologist and coauthor of You Will Get Through This: A Mental Health First-Aid Kit.

• Find a Therapist
• Find a Treatment Center
• Find a Psychiatrist
• Find a Support Group
• Find Online Therapy
• International
• New Zealand
• South Africa
• Switzerland
• Asperger's
• Bipolar Disorder
• Chronic Pain
• Eating Disorders
• Passive Aggression
• Personality
• Goal Setting
• Positive Psychology
• Stopping Smoking
• Low Sexual Desire
• Relationships
• Child Development
• Self Tests NEW
• Therapy Center
• Diagnosis Dictionary
• Types of Therapy

At any moment, someone’s aggravating behavior or our own bad luck can set us off on an emotional spiral that threatens to derail our entire day. Here’s how we can face our triggers with less reactivity so that we can get on with our lives.

• Emotional Intelligence
• Gaslighting
• Affective Forecasting
• Neuroscience