mixture and distance problem solving

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 6: Polynomials

6.8 Mixture and Solution Word Problems

Solving mixture problems generally involves solving systems of equations. Mixture problems are ones in which two different solutions are mixed together, resulting in a new, final solution. Using a table will help to set up and solve these problems. The basic structure of this table is shown below:

The first column in the table (Name) is used to identify the fluids or objects being mixed in the problem. The second column (Amount) identifies the amounts of each of the fluids or objects. The third column (Value) is used for the value of each object or the percentage of concentration of each fluid. The last column (Equation) contains the product of the Amount times the Value or Concentration.

Example 6.8.1

Jasnah has 70 mL of a 50% methane solution. How much of a 80% solution must she add so the final solution is 60% methane? Find the equation.

• The solution names are 50% (S 50 ), 60% (S 60 ), and 80% (S 80 ).
• The amounts are S 50 = 70 mL, S 80 , and S 60 = 70 mL + S 80 .
• The concentrations are S 50 = 0.50, S 60 = 0.60, and S 80 = 0.80.

The equation derived from this data is 0.50 (70 mL) + 0.80 (S 80 ) = 0.60 (70 mL + S 80 ).

Example 6.8.2

Sally and Terry blended a coffee mix that sells for [latex]\$2.50[/latex] by mixing two types of coffee. If they used 40 mL of a coffee that costs [latex]\$3.00,[/latex] how much of another coffee costing [latex]\$1.50[/latex] did they mix with the first?

The equation derived from this data is:

[latex]\begin{array}{ccccccc} 1.50(C_{1.50})&+&3.00(40)&=&2.50(40&+&C_{1.50}) \\ 1.50(C_{1.50})&+&120&=&100&+&2.50(C_{1.50}) \\ -2.50(C_{1.50})&-&120&=&-120&-&2.50(C_{1.50}) \\ \hline &&-1.00(C_{1.50})&=&-20&& \\ \\ &&(C_{1.50})&=&\dfrac{-20}{-1}&& \\ \\ &&C_{1.50}&=&20&& \end{array}[/latex]

This means 20 mL of the coffee selling for [latex]\$1.50[/latex] is needed for the mix.

Example 6.8.3

Nick and Chloe have two grades of milk from their small dairy herd: one that is 24% butterfat and another that is 18% butterfat. How much of each should they use to end up with 42 litres of 20% butterfat?

The equation derived from this data is:

[latex]\begin{array}{rrrrrrr} 0.24(B_{24})&+&0.18(42&- &B_{24})&=&0.20(42) \\ 0.24(B_{24})&+&7.56&-&0.18(B_{24})&=&8.4 \\ &-&7.56&&&&-7.56 \\ \hline &&&&0.06(B_{24})&=&0.84 \\ \\ &&&&B_{24}&=&\dfrac{0.84}{0.06} \\ \\ &&&&B_{24}&=&14 \end{array}[/latex]

This means 14 litres of the 24% buttermilk, and 28 litres of the 18% buttermilk is needed.

Example 6.8.4

In Natasha’s candy shop, chocolate, which sells for [latex]\$4[/latex] a kilogram, is mixed with nuts, which are sold for [latex]\$2.50[/latex] a kilogram. Chocolate and nuts are combined to form a chocolate-nut candy, which sells for [latex]\$3.50[/latex] a kilogram. How much of each are used to make 30 kilograms of the mixture?

[latex]\begin{array}{rrrrrrl} 4.00(C)&+&2.50(30&-&C)&=&3.50(30) \\ 4.00(C)&+&75&-&2.50(C)&=&105 \\ &-&75&&&&-75 \\ \hline &&&&1.50(C)&=&30 \\ \\ &&&&C&=&\dfrac{30}{1.50} \\ \\ &&&&C&=&20 \end{array}[/latex]

Therefore, 20 kg of chocolate is needed for the mixture.

With mixture problems, there is often mixing with a pure solution or using water, which contains none of the chemical of interest. For pure solutions, the concentration is 100%. For water, the concentration is 0%. This is shown in the following example.

Example 6.8.5

Joey is making a a 65% antifreeze solution using pure antifreeze mixed with water. How much of each should be used to make 70 litres?

[latex]\begin{array}{rrrrl} 1.00(A)&+&0.00(70-A)&=&0.65(0.70) \\ &&1.00A&=&45.5 \\ &&A&=&45.5 \\ \end{array}[/latex]

This means the amount of water added is 70 L − 45.5 L = 24.5 L.

For questions 1 to 9, write the equations that define the relationship.

• A tank contains 8000 litres of a solution that is 40% acid. How much water should be added to make a solution that is 30% acid?
• How much pure antifreeze should be added to 5 litres of a 30% mixture of antifreeze to make a solution that is 50% antifreeze?
• You have 12 kilograms of 10% saline solution and another solution of 3% strength. How many kilograms of the second should be added to the first in order to get a 5% solution?
• How much pure alcohol must be added to 24 litres of a 14% solution of alcohol in order to produce a 20% solution?
• How many litres of a blue dye that costs [latex]\$1.60[/latex] per litre must be mixed with 18 litres of magenta dye that costs [latex]\$2.50[/latex] per litre to make a mixture that costs [latex]\$1.90[/latex] per litre?
• How many grams of pure acid must be added to 40 grams of a 20% acid solution to make a solution which is 36% acid?
• A 100-kg bag of animal feed is 40% oats. How many kilograms of pure oats must be added to this feed to produce a blend of 50% oats?
• A 20-gram alloy of platinum that costs [latex]\$220[/latex] per gram is mixed with an alloy that costs [latex]\$400[/latex] per gram. How many grams of the [latex]\$400[/latex] alloy should be used to make an alloy that costs [latex]\$300[/latex] per gram?
• How many kilograms of tea that cost [latex]\$4.20[/latex] per kilogram must be mixed with 12 kilograms of tea that cost [latex]\$2.25[/latex] per kilogram to make a mixture that costs [latex]\$3.40[/latex] per kilogram?

Solve questions 10 to 21.

• How many litres of a solvent that costs [latex]\$80[/latex] per litre must be mixed with 6 litres of a solvent that costs [latex]\$25[/latex] per litre to make a solvent that costs [latex]\$36[/latex] per litre?
• How many kilograms of hard candy that cost [latex]\$7.50[/latex] per kg must be mixed with 24 kg of jelly beans that cost [latex]\$3.25[/latex] per kg to make a mixture that sells for [latex]\$4.50[/latex] per kg?
• How many kilograms of soil supplement that costs [latex]\$7.00[/latex] per kg must be mixed with 20 kg of aluminum nitrate that costs [latex]\$3.50[/latex] per kg to make a fertilizer that costs [latex]\$4.50[/latex] per kg?
• A candy mix sells for [latex]\$2.20[/latex] per kg. It contains chocolates worth [latex]\$1.80[/latex] per kg and other candy worth [latex]\$3.00[/latex] per kg. How much of each are in 15 kg of the mixture?
• A certain grade of milk contains 10% butterfat and a certain grade of cream 60% butterfat. How many litres of each must be taken so as to obtain a mixture of 100 litres that will be 45% butterfat?
• Solution A is 50% acid and solution B is 80% acid. How much of each should be used to make 100 cc of a solution that is 68% acid?
• A paint that contains 21% green dye is mixed with a paint that contains 15% green dye. How many litres of each must be used to make 600 litres of paint that is 19% green dye?
• How many kilograms of coffee that is 40% java beans must be mixed with coffee that is 30% java beans to make an 80-kg coffee blend that is 32% java beans?
• A caterer needs to make a slightly alcoholic fruit punch that has a strength of 6% alcohol. How many litres of fruit juice must be added to 3.75 litres of 40% alcohol?
• A mechanic needs to dilute a 70% antifreeze solution to make 20 litres of 18% strength. How many litres of water must be added?
• How many millilitres of water must be added to 50 millilitres of 100% acid to make a 40% solution?
• How many litres of water need to be evaporated from 50 litres of a 12% salt solution to produce a 15% salt solution?

Answer Key 6.8

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

4.3 Solve Mixture Applications with Systems of Equations

Learning objectives.

• Solve mixture applications
• Solve interest applications

Solve applications of cost and revenue functions

Be prepared 4.3.

Before you get started, take this readiness quiz.

• Multiply: 4.025 ( 1,562 ) . 4.025 ( 1,562 ) . If you missed this problem, review Example 1.36 .
• Write 8.2% as a decimal. If you missed this problem, review Example 1.40 .
• Earl’s dinner bill came to $32.50 and he wanted to leave an 18% tip. How much should the tip be? If you missed this problem, review Example 2.20 .

Solve Mixture Applications

Mixture application involve combining two or more quantities. When we solved mixture applications with coins and tickets earlier, we started by creating a table so we could organize the information. For a coin example with nickels and dimes, the table looked like this:

Using one variable meant that we had to relate the number of nickels and the number of dimes. We had to decide if we were going to let n be the number of nickels and then write the number of dimes in terms of n , or if we would let d be the number of dimes and write the number of nickels in terms of d .

Now that we know how to solve systems of equations with two variables, we’ll just let n be the number of nickels and d be the number of dimes. We’ll write one equation based on the total value column, like we did before, and the other equation will come from the number column.

For the first example, we’ll do a ticket problem where the ticket prices are in whole dollars, so we won’t need to use decimals just yet.

Example 4.24

Translate to a system of equations and solve:

A science center sold 1,363 tickets on a busy weekend. The receipts totaled $12,146. How many $12 adult tickets and how many $7 child tickets were sold?

Try It 4.47

The ticket office at the zoo sold 553 tickets one day. The receipts totaled $3,936. How many $9 adult tickets and how many $6 child tickets were sold?

Try It 4.48

The box office at a movie theater sold 147 tickets for the evening show, and receipts totaled $1,302. How many $11 adult and how many $8 child tickets were sold?

In the next example, we’ll solve a coin problem. Now that we know how to work with systems of two variables, naming the variables in the ‘number’ column will be easy.

Example 4.25

Juan has a pocketful of nickels and dimes. The total value of the coins is $8.10. The number of dimes is 9 less than twice the number of nickels. How many nickels and how many dimes does Juan have?

Try It 4.49

Matilda has a handful of quarters and dimes, with a total value of $8.55. The number of quarters is 3 more than twice the number of dimes. How many dimes and how many quarters does she have?

Try It 4.50

Priam has a collection of nickels and quarters, with a total value of $7.30. The number of nickels is six less than three times the number of quarters. How many nickels and how many quarters does he have?

Some mixture applications involve combining foods or drinks. Example situations might include combining raisins and nuts to make a trail mix or using two types of coffee beans to make a blend.

Example 4.26

Carson wants to make 20 pounds of trail mix using nuts and chocolate chips. His budget requires that the trail mix costs him $7.60. per pound. Nuts cost $9.00 per pound and chocolate chips cost $2.00 per pound. How many pounds of nuts and how many pounds of chocolate chips should he use?

Try It 4.51

Greta wants to make 5 pounds of a nut mix using peanuts and cashews. Her budget requires the mixture to cost her $6 per pound. Peanuts are $4 per pound and cashews are $9 per pound. How many pounds of peanuts and how many pounds of cashews should she use?

Try It 4.52

Sammy has most of the ingredients he needs to make a large batch of chili. The only items he lacks are beans and ground beef. He needs a total of 20 pounds combined of beans and ground beef and has a budget of $3 per pound. The price of beans is $1 per pound and the price of ground beef is $5 per pound. How many pounds of beans and how many pounds of ground beef should he purchase?

Another application of mixture problems relates to concentrated cleaning supplies, other chemicals, and mixed drinks. The concentration is given as a percent. For example, a 20% concentrated household cleanser means that 20% of the total amount is cleanser, and the rest is water. To make 35 ounces of a 20% concentration, you mix 7 ounces (20% of 35) of the cleanser with 28 ounces of water.

For these kinds of mixture problems, we’ll use “percent” instead of “value” for one of the columns in our table.

Example 4.27

Sasheena is lab assistant at her community college. She needs to make 200 milliliters of a 40% solution of sulfuric acid for a lab experiment. The lab has only 25% and 50% solutions in the storeroom. How much should she mix of the 25% and the 50% solutions to make the 40% solution?

Try It 4.53

LeBron needs 150 milliliters of a 30% solution of sulfuric acid for a lab experiment but only has access to a 25% and a 50% solution. How much of the 25% and how much of the 50% solution should he mix to make the 30% solution?

Try It 4.54

Anatole needs to make 250 milliliters of a 25% solution of hydrochloric acid for a lab experiment. The lab only has a 10% solution and a 40% solution in the storeroom. How much of the 10% and how much of the 40% solutions should he mix to make the 25% solution?

Solve Interest Applications

The formula to model simple interest applications is I = P r t . I = P r t . Interest, I , is the product of the principal, P , the rate, r , and the time, t . In our work here, we will calculate the interest earned in one year, so t will be 1.

We modify the column titles in the mixture table to show the formula for interest, as you’ll see in the next example.

Example 4.28

Adnan has $40,000 to invest and hopes to earn 7.1 % 7.1 % interest per year. He will put some of the money into a stock fund that earns 8% per year and the rest into bonds that earns 3% per year. How much money should he put into each fund?

Did you notice that the Principal column represents the total amount of money invested while the Interest column represents only the interest earned? Likewise, the first equation in our system, s + b = 40,000 , s + b = 40,000 , represents the total amount of money invested and the second equation, 0.08 s + 0.03 b = 0.071 ( 40,000 ) , 0.08 s + 0.03 b = 0.071 ( 40,000 ) , represents the interest earned.

Try It 4.55

Leon had $50,000 to invest and hopes to earn 6.2 % 6.2 % interest per year. He will put some of the money into a stock fund that earns 7% per year and the rest in to a savings account that earns 2% per year. How much money should he put into each fund?

Try It 4.56

Julius invested $7000 into two stock investments. One stock paid 11% interest and the other stock paid 13% interest. He earned 12.5 % 12.5 % interest on the total investment. How much money did he put in each stock?

The next example requires that we find the principal given the amount of interest earned.

Example 4.29

Rosie owes $21,540 on her two student loans. The interest rate on her bank loan is 10.5 % 10.5 % and the interest rate on the federal loan is 5.9 % . 5.9 % . The total amount of interest she paid last year was $ 1,669.68 . $ 1,669.68 . What was the principal for each loan?

Try It 4.57

Laura owes $18,000 on her student loans. The interest rate on the bank loan is 2.5% and the interest rate on the federal loan is 6.9%. The total amount of interest she paid last year was $1,066. What was the principal for each loan?

Try It 4.58

Jill’s Sandwich Shoppe owes $65,200 on two business loans, one at 4.5% interest and the other at 7.2% interest. The total amount of interest owed last year was $3,582. What was the principal for each loan?

Suppose a company makes and sells x units of a product. The cost to the company is the total costs to produce x units. This is the cost to manufacture for each unit times x , the number of units manufactured, plus the fixed costs.

The revenue is the money the company brings in as a result of selling x units. This is the selling price of each unit times the number of units sold.

When the costs equal the revenue we say the business has reached the break-even point .

Cost and Revenue Functions

The cost function is the cost to manufacture each unit times x , the number of units manufactured, plus the fixed costs.

The revenue function is the selling price of each unit times x , the number of units sold.

The break-even point is when the revenue equals the costs.

Example 4.30

The manufacturer of a weight training bench spends $105 to build each bench and sells them for $245. The manufacturer also has fixed costs each month of $7,000.

ⓐ Find the cost function C when x benches are manufactured.

ⓑ Find the revenue function R when x benches are sold.

ⓒ Show the break-even point by graphing both the Revenue and Cost functions on the same grid.

ⓓ Find the break-even point. Interpret what the break-even point means.

ⓐ The manufacturer has $7,000 of fixed costs no matter how many weight training benches it produces. In addition to the fixed costs, the manufacturer also spends $105 to produce each bench. Suppose x benches are sold.

Write the general Cost function formula. C ( x ) = ( cost per unit ) · x + fixed costs Substitute in the cost values. C ( x ) = 105 x + 7000 Write the general Cost function formula. C ( x ) = ( cost per unit ) · x + fixed costs Substitute in the cost values. C ( x ) = 105 x + 7000

ⓑ The manufacturer sells each weight training bench for $245. We get the total revenue by multiplying the revenue per unit times the number of units sold.

Write the general Revenue function. R ( x ) = ( selling price per unit ) · x Substitute in the revenue per unit. R ( x ) = 245 x Write the general Revenue function. R ( x ) = ( selling price per unit ) · x Substitute in the revenue per unit. R ( x ) = 245 x

ⓒ Essentially we have a system of linear equations. We will show the graph of the system as this helps make the idea of a break-even point more visual.

ⓓ To find the actual value, we remember the break-even point occurs when costs equal revenue.

Write the break-even formula. C ( x ) = R ( x ) 105 x + 7000 = 245 x Solve. 7000 = 140 x 50 = x Write the break-even formula. C ( x ) = R ( x ) 105 x + 7000 = 245 x Solve. 7000 = 140 x 50 = x

When 50 benches are sold, the costs equal the revenue.

When 50 benches are sold, the revenue and costs are both $12,250. Notice this corresponds to the ordered pair ( 50 , 12,250 ) . ( 50 , 12,250 ) .

Try It 4.59

The manufacturer of a weight training bench spends $15 to build each bench and sells them for $32. The manufacturer also has fixed costs each month of $25,500.

Try It 4.60

The manufacturer of a weight training bench spends $120 to build each bench and sells them for $170. The manufacturer also has fixed costs each month of $150,000.

Access this online resource for additional instruction and practice with interest and mixtures.

• Interest and Mixtures

Section 4.3 Exercises

Practice makes perfect.

In the following exercises, translate to a system of equations and solve.

Tickets to a Broadway show cost $35 for adults and $15 for children. The total receipts for 1650 tickets at one performance were $47,150. How many adult and how many child tickets were sold?

Tickets for the Cirque du Soleil show are $70 for adults and $50 for children. One evening performance had a total of 300 tickets sold and the receipts totaled $17,200. How many adult and how many child tickets were sold?

Tickets for an Amtrak train cost $10 for children and $22 for adults. Josie paid $1200 for a total of 72 tickets. How many children tickets and how many adult tickets did Josie buy?

Tickets for a Minnesota Twins baseball game are $69 for Main Level seats and $39 for Terrace Level seats. A group of sixteen friends went to the game and spent a total of $804 for the tickets. How many of Main Level and how many Terrace Level tickets did they buy?

Tickets for a dance recital cost $15 for adults and $7 dollars for children. The dance company sold 253 tickets and the total receipts were $2771. How many adult tickets and how many child tickets were sold?

Tickets for the community fair cost $12 for adults and $5 dollars for children. On the first day of the fair, 312 tickets were sold for a total of $2204. How many adult tickets and how many child tickets were sold?

Brandon has a cup of quarters and dimes with a total value of $ 3.80 . $ 3.80 . The number of quarters is four less than twice the number of quarters. How many quarters and how many dimes does Brandon have?

Sherri saves nickels and dimes in a coin purse for her daughter. The total value of the coins in the purse is $ 0.95 . $ 0.95 . The number of nickels is two less than five times the number of dimes. How many nickels and how many dimes are in the coin purse?

Peter has been saving his loose change for several days. When he counted his quarters and nickels, he found they had a total value $ 13.10 . $ 13.10 . The number of quarters was fifteen more than three times the number of dimes. How many quarters and how many dimes did Peter have?

Lucinda had a pocketful of dimes and quarters with a value of $ 6.20 . $ 6.20 . The number of dimes is eighteen more than three times the number of quarters. How many dimes and how many quarters does Lucinda have?

A cashier has 30 bills, all of which are $10 or $20 bills. The total value of the money is $460. How many of each type of bill does the cashier have?

A cashier has 54 bills, all of which are $10 or $20 bills. The total value of the money is $910. How many of each type of bill does the cashier have?

Marissa wants to blend candy selling for $ 1.80 $ 1.80 per pound with candy costing $ 1.20 $ 1.20 per pound to get a mixture that costs her $ 1.40 $ 1.40 per pound to make. She wants to make 90 pounds of the candy blend. How many pounds of each type of candy should she use?

How many pounds of nuts selling for $6 per pound and raisins selling for $3 per pound should Kurt combine to obtain 120 pounds of trail mix that cost him $5 per pound?

Hannah has to make twenty-five gallons of punch for a potluck. The punch is made of soda and fruit drink. The cost of the soda is $ 1.79 $ 1.79 per gallon and the cost of the fruit drink is $ 2.49 $ 2.49 per gallon. Hannah’s budget requires that the punch cost $ 2.21 $ 2.21 per gallon. How many gallons of soda and how many gallons of fruit drink does she need?

Joseph would like to make twelve pounds of a coffee blend at a cost of $6 per pound. He blends Ground Chicory at $5 a pound with Jamaican Blue Mountain at $9 per pound. How much of each type of coffee should he use?

Julia and her husband own a coffee shop. They experimented with mixing a City Roast Columbian coffee that cost $7.80 per pound with French Roast Columbian coffee that cost $8.10 per pound to make a twenty-pound blend. Their blend should cost them $7.92 per pound. How much of each type of coffee should they buy?

Twelve-year old Melody wants to sell bags of mixed candy at her lemonade stand. She will mix M&M’s that cost $4.89 per bag and Reese’s Pieces that cost $3.79 per bag to get a total of twenty-five bags of mixed candy. Melody wants the bags of mixed candy to cost her $4.23 a bag to make. How many bags of M&M’s and how many bags of Reese’s Pieces should she use?

Jotham needs 70 liters of a 50% solution of an alcohol solution. He has a 30% and an 80% solution available. How many liters of the 30% and how many liters of the 80% solutions should he mix to make the 50% solution?

Joy is preparing 15 liters of a 25% saline solution. She only has 40% and 10% solution in her lab. How many liters of the 40% and how many liters of the 10% should she mix to make the 25% solution?

A scientist needs 65 liters of a 15% alcohol solution. She has available a 25% and a 12% solution. How many liters of the 25% and how many liters of the 12% solutions should she mix to make the 15% solution?

A scientist needs 120 milliliters of a 20% acid solution for an experiment. The lab has available a 25% and a 10% solution. How many liters of the 25% and how many liters of the 10% solutions should the scientist mix to make the 20% solution?

A 40% antifreeze solution is to be mixed with a 70% antifreeze solution to get 240 liters of a 50% solution. How many liters of the 40% and how many liters of the 70% solutions will be used?

A 90% antifreeze solution is to be mixed with a 75% antifreeze solution to get 360 liters of an 85% solution. How many liters of the 90% and how many liters of the 75% solutions will be used?

Hattie had $3000 to invest and wants to earn 10.6 % 10.6 % interest per year. She will put some of the money into an account that earns 12% per year and the rest into an account that earns 10% per year. How much money should she put into each account?

Carol invested $2560 into two accounts. One account paid 8% interest and the other paid 6% interest. She earned 7.25 % 7.25 % interest on the total investment. How much money did she put in each account?

Sam invested $48,000, some at 6% interest and the rest at 10%. How much did he invest at each rate if he received $4000 in interest in one year?

Arnold invested $64,000, some at 5.5 % 5.5 % interest and the rest at 9%. How much did he invest at each rate if he received $4500 in interest in one year?

After four years in college, Josie owes $65, 800 in student loans. The interest rate on the federal loans is 4.5 % 4.5 % and the rate on the private bank loans is 2%. The total interest she owes for one year was $ 2878.50 . $ 2878.50 . What is the amount of each loan?

Mark wants to invest $10,000 to pay for his daughter’s wedding next year. He will invest some of the money in a short term CD that pays 12% interest and the rest in a money market savings account that pays 5% interest. How much should he invest at each rate if he wants to earn $1095 in interest in one year?

A trust fund worth $25,000 is invested in two different portfolios. This year, one portfolio is expected to earn 5.25 % 5.25 % interest and the other is expected to earn 4%. Plans are for the total interest on the fund to be $1150 in one year. How much money should be invested at each rate?

A business has two loans totaling $85,000. One loan has a rate of 6% and the other has a rate of 4.5% This year, the business expects to pay $4,650 in interest on the two loans. How much is each loan?

Solve Applications of Cost and Revenue Functions

The manufacturer of an energy drink spends $1.20 to make each drink and sells them for $2. The manufacturer also has fixed costs each month of $8,000.

ⓐ Find the cost function C when x energy drinks are manufactured.

ⓑ Find the revenue function R when x drinks are sold.

The manufacturer of a water bottle spends $5 to build each bottle and sells them for $10. The manufacturer also has fixed costs each month of $6500. ⓐ Find the cost function C when x bottles are manufactured. ⓑ Find the revenue function R when x bottles are sold. ⓒ Show the break-even point by graphing both the Revenue and Cost functions on the same grid. ⓓ Find the break-even point. Interpret what the break-even point means.

Writing Exercises

Take a handful of two types of coins, and write a problem similar to Example 4.25 relating the total number of coins and their total value. Set up a system of equations to describe your situation and then solve it.

In Example 4.28 , we used elimination to solve the system of equations { s + b = 40,000 0.08 s + 0.03 b = 0.071 ( 40,000 ) . { s + b = 40,000 0.08 s + 0.03 b = 0.071 ( 40,000 ) .

Could you have used substitution or elimination to solve this system? Why?

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra/pages/1-introduction

• Authors: Lynn Marecek
• Publisher/website: OpenStax
• Book title: Intermediate Algebra
• Publication date: Mar 14, 2017
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra/pages/4-3-solve-mixture-applications-with-systems-of-equations

© Feb 9, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Algebra: Mixture Word Problems

In these lessons, we will learn how to solve mixture word problems using algebra.

Related Pages Mixture Problems Solving Mixture Word Problems Using Algebra More Algebra Lessons

What Are Mixture Problems?

Mixture problems are word problems where items or quantities of different values are mixed together.

Sometimes different liquids are mixed together changing the concentration of the mixture as shown in example 1 , example 2 and example 3 .

At other times, quantities of different costs are mixed together as shown in [example 4](#mix

We recommend using a table to organize your information for mixture problems. Using a table allows you to think of one number at a time instead of trying to handle the whole mixture problem at once.

We will show you how it is done by the following examples of mixture problems:

• Adding to the Solution
• Removing from the Solution
• Replacing the Solution
• Mixing Quantities of Different Costs

How To Solve Mixture Problems When We Are Adding To The Solution?

Mixture Problems: Example 1: John has 20 ounces of a 20% of salt solution. How much salt should he add to make it a 25% solution?

Solution: Set up a table for salt using the information from the question.

How To Solve Mixture Problems When We Are Removing From The Solution?

Mixture Problems: Example 2: John has 20 ounces of a 20% of salt solution. How much water should he evaporate to make it a 3 0% solution?

Solution: Set up a table for water . The water is removed from the original solution.

How To Solve Mixture Problems When We Are Replacing The Solution?

Mixture Problems: Example 3: A tank has a capacity of 10 gallons. When it is full, it contains 15% alcohol. How many gallons must be replaced by an 80% alcohol solution to give 10 gallons of 70% solution?

Solution: Set up a table for alcohol . The alcohol is replaced: an amount of 15% alcohol is removed and the same amount of 80% alcohol is added.

Mixture Word Problems: Mixing Quantities Of Different Costs

Mixture Problems: Example 4: How many pounds of chocolate worth $1.20 a pound must be mixed with 10 pounds of chocolate worth 90 cents a pound to produce a mixture worth $1.00 a pound?

Solution: Set up a table for the chocolates with different costs.

How To Set Up And Solve Mixture Word Problems?

Some word problems using systems of equations involve mixing two quantities with different prices. To solve mixture problems, knowledge of solving systems of equations. is necessary. Most often, these problems will have two variables, but more advanced problems have systems of equations with three variables. Other types of word problems using systems of equations include rate word problems and work word problems.

How To Solve Acid Solution Problems?

Example: The mad scientist has one solution that is 30% acid and another solution that is 18% acid. How much of each should he use to get 300 L of a solution that is 21% acid?

Example: How much pure acid must be mixed with 200 mL of 5% acid to get a 25% acid?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Reset password New user? Sign up

Existing user? Log in

Solving Mixture Problems

Already have an account? Log in here.

Mixture problems involve combining two or more things and determining some characteristic of either the ingredients or the resulting mixture. For example, we might want to know how much water to add to dilute a saline solution, or we might want to determine the percentage of concentrate in a jug of orange juice.

Introduction to Mixtures

Using a table to problem solve, practice problems.

We can use fractions, ratios, or percentages to describe quantities in mixtures.

If 200 grams of a saline solution has 40 grams of salt, what percentage of the solution is salt? Answer \(\frac{40}{200} = 0.20 = 20\%\) of the solution is salt.

If each can of orange juice concentrate contains the same amount of concentrate, which recipe will make the drink that is most orangey?

There is a general strategy for solving these mixture problems that uses simple algebra organized with a chart.

How much 40% rubbing alcohol do we need to add to 90% rubbing alcohol to make a 50% solution of rubbing alcohol? We could organize the data we are given in the following chart: Solution Type Concentration Amount of Solution Amount of Pure Alcohol 40% rubbing alcohol 0.4 ? liters ? liters 90% rubbing alcohol 0.9 ? liters ? liters 50% rubbing alcohol 0.5 10 liters \(0.5(10) = 5\) liters In general, the rows of the chart are the mixture types that you have. The columns describe the amount of each compound you have and the concentration of that component in each mixture (represented as a decimal). When you don't have some of the information needed to fill in the cart, use a variable instead. Solution Type Concentration Amount of Solution Amount of Pure Compound 40% rubbing alcohol 0.4 \(x\) \(0.4(x)\) 90% rubbing alcohol 0.9 \(10-x\) \(0.9(10-x)\) 50% rubbing alcohol 0.5 10 \(0.5(10) = 5\) The amount of 40% solution that we'll need is unknown (so make it \(x\)). The amount of 90% solution that we'll need is also unknown, but must be \(10-x\) liters so that we'll, in total, make 10 liters of the final solution. The amount of alcohol that each part of the mixture adds to the final result is equal to the amount of each solution mixed in, times the fraction of alcohol that that solution is made from. To use this chart to solve the problem, we will use the fourth column as an equation to solve for \(x.\) The 10 liters of our final mixture must have a total volume of 5 liters of alcohol in it in order to be 50% alcohol. Those 5 liters must come from a combination of the amount of 40% solution we mix in and the amount of 90% solution. If the volume (in liters) of 40% solution that we mix in is \(x,\) then \(0.4x\) will be the volume (in liters) of the amount of alcohol contributed. Similarly, \(0.9(10-x)\) will be the amount of alcohol contributed by the \(10-x\) liters of 90% alcohol solution that we add. Therefore, in total, \(0.4x + 0.9(10-x)\) must be equal to the 5 total liters we'll need in the final solution to make it 50% alcohol. Solving the equation, \[\begin{align} 0.4x + (9 - 0.9x) &= 5\\ -0.5x + 9 &= 5\\ 0.5x &= 4\\ \Rightarrow x &= \frac{4}{0.5}= 8. \end{align}\] Therefore, we need \(x = 8\) liters of the 40% solution.

How many grams of pure water must be added to 40 grams of a 10% saline solution to make a saline solution that is 5% salt? Answer Let's set up a table to solve this problem, using \(x\) to represent the number of grams of water that must be added. Solution Type Concentration Amount of Solution Total Amount of Salt water 0 \(x\) 0 10% solution 0.1 40 \((0.1)(40)\) 5% solution 0.05 40+\(x\) \((0.05)(40+x)\) Because the total amount of salt remains the same after we add the water, we can set up and solve the following equation: \[\begin{align} (0.1)(40)&=(0.05)(40+x) \\ 4 &= 2 + 0.05x \\ x&=40.\end{align}\] We need to add \(40 \) grams of pure water to create the solution that is \(5\%\) salt.

I have a 100 ml mixture that is 20% isopropyl alcohol (80 ml of water and 20 ml of isopropyl alcohol).

How much more alcohol do I need to add to make the mixture 25% alcohol?

There is a 40 litre solution of milk and water in which the concentration of milk is 72%. How much water must be added to this solution to make it a solution in which the concentration of milk is 60% ?

Let's practice using the strategies from above on a variety of problems.

Jill mixes 100 liters of A-beverage that contains 45% juice with 200 liters of B-beverage. The resulting C-beverage is 30% fruit juice. What is the percent of fruit juice in the 200 liters of the B-beverage? Answer Let's begin by making a table to show what we know. Beverage Liters of Beverage Concentration Liters of Juice Beverage A 100 0.45 \((0.45)(100) = 45\) Beverage B 200 \(x\) \(200x\) Beverage C 300 0.30 \((0.30)(300)=90\) The total number of liters of juice in Beverages A and B must equal 90, so \[\begin{align} 45 + 200x &= 90 \\ 200x &= 45 \\ 0.225 &= x.\end{align}\] The concentration of juice in Beverage B is 22.5%.

Unequal amounts of 40% and 10% acid solutions were mixed and the resulting mixture was 30% concentrated. However, the required concentration is 25%, so the Chemist added 300 cubic meters of 20% acid solution in order to get the required concentration. What was the original amount of 40% acid solution?

Write only the quantity without the units (cubic meters).

Legend: wt = weight

Strawberries contain about 15 wt% solids and 85 wt% water. To make strawberry jam, crushed strawberries and sugar are mixed in a 45:55 mass ratio, and the mixture is heated to evaporate water until the residue contains one-third water by mass.

Question: 1.) Calculate how many pounds of strawberries are needed to make a pound of jam.

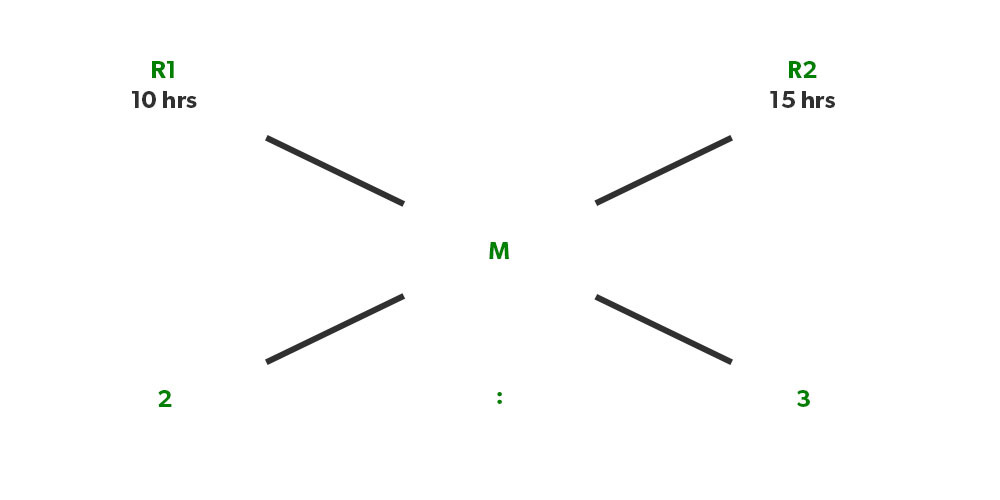
In a mixture of 60 litres, the ratio of milk and water 2 : 1. If this ratio is to be 1 : 2, then the quanity of water to be further added is:

Problem Loading...

Note Loading...

Set Loading...

Mixture Problems With Solutions

Mixture problems and their solutions are presented along with their solutions. Percentages are also used to solve these types of problems.

Problem 1: How many liters of 20% alcohol solution should be added to 40 liters of a 50% alcohol solution to make a 30% solution?

Solution to Problem 1: Let x be the quantity of the 20% alcohol solution to be added to the 40 liters of a 50% alcohol. Let y be the quantity of the final 30% solution. Hence x + 40 = y We shall now express mathematically that the quantity of alcohol in x liters plus the quantity of alcohol in the 40 liters is equal to the quantity of alcohol in y liters. But remember the alcohol is measured in percentage term. 20% x + 50% * 40 = 30% y Substitute y by x + 40 in the last equation to obtain. 20% x + 50% * 40 = 30% (x + 40) Change percentages into fractions. 20 x / 100 + 50 * 40 / 100= 30 x / 100 + 30 * 40 / 100 Multiply all terms by 100 to simplify. 20 x + 50 * 40 = 30 x + 30 * 40 Solve for x. x = 80 liters 80 liters of 20% alcohol is be added to 40 liters of a 50% alcohol solution to make a 30% solution.

Problem 2: John wants to make a 100 ml of 5% alcohol solution mixing a quantity of a 2% alcohol solution with a 7% alcohol solution. What are the quantities of each of the two solutions (2% and 7%) he has to use?

Solution to Problem 2: Let x and y be the quantities of the 2% and 7% alcohol solutions to be used to make 100 ml. Hence x + y = 100 We now write mathematically that the quantity of alcohol in x ml plus the quantity of alcohol in y ml is equal to the quantity of alcohol in 100 ml. 2% x + 7% y = 5% 100 The first equation gives y = 100 - x. Substitute in the last equation to obtain 2% x + 7% (100 - x) = 5% 100 Multiply by 100 and simplify 2 x + 700 - 7 x = 5 * 100 Solve for x x = 40 ml Substitute x by 40 in the first equation to find y y = 100 - x = 60 ml

Problem 3: Sterling Silver is 92.5% pure silver. How many grams of Sterling Silver must be mixed to a 90% Silver alloy to obtain a 500g of a 91% Silver alloy?

Solution to Problem 3: Let x and y be the weights, in grams, of sterling silver and of the 90% alloy to make the 500 grams at 91%. Hence x + y =500 The number of grams of pure silver in x plus the number of grams of pure silver in y is equal to the number of grams of pure silver in the 500 grams. The pure silver is given in percentage forms. Hence 92.5% x + 90% y = 91% 500 Substitute y by 500 - x in the last equation to write 92.5% x + 90% (500 - x) = 91% 500 Simplify and solve 92.5 x + 45000 - 90 x = 45500 x = 200 grams. 200 grams of Sterling Silver is needed to make the 91% alloy.

Problem 4: How many Kilograms of Pure water is to be added to 100 Kilograms of a 30% saline solution to make it a 10% saline solution.

Solution to Problem 4: Let x be the weights, in Kilograms, of pure water to be added. Let y be the weight, in Kilograms, of the 10% solution. Hence x + 100 = y Let us now express the fact that the amount of salt in the pure water (which 0) plus the amount of salt in the 30% solution is equal to the amount of salt in the final saline solution at 10%. 0 + 30% 100 = 10% y Substitute y by x + 100 in the last equation and solve. 30% 100 = 10% (x + 100) Solve for x. x = 200 Kilograms.

Problem 5: A 50 ml after-shave lotion at 30% alcohol is mixed with 30 ml of pure water. What is the percentage of alcohol in the new solution?

Solution to Problem 5: The amount of the final mixture is given by 50 ml + 30 ml = 80 ml The amount of alcohol is equal to the amount of alcohol in pure water ( which is 0) plus the amount of alcohol in the 30% solution. Let x be the percentage of alcohol in the final solution. Hence 0 + 30% 50 ml = x (80) Solve for x x = 0.1817 = 18.75%

Problem 6: You add x ml of a 25% alcohol solution to a 200 ml of a 10% alcohol solution to obtain another solution. Find the amount of alcohol in the final solution in terms of x. Find the ratio, in terms of x, of the alcohol in the final solution to the total amount of the solution. What do you think will happen if x is very large? Find x so that the final solution has a percentage of 15%.

Solution to Problem 6: Let us first find the amount of alcohol in the 10% solution of 200 ml. 200 * 10% = 20 ml The amount of alcohol in the x ml of 25% solution is given by 25% x = 0.25 x The total amount of alcohol in the final solution is given by 20 + 0.25 x The ratio of alcohol in the final solution to the total amount of the solution is given by [ ( 20 + 0.25 x ) / (x + 200)] If x becomes very large in the above formula for the ratio, then the ratio becomes close to 0.25 or 25% (The above function is a rational function and 0.25 is its horizontal asymptote). This means that if you increase the amount x of the 25% solution, this will dominate and the final solution will be very close to a 25% solution. To have a percentage of 15%, we need to have [ ( 20 + 0.25 x ) / (x + 200)] = 15% = 0.15 Solve the above equation for x 20 + 0.25 x = 0.15 * (x + 200) x = 100 ml

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Precalculus

Course: precalculus   >   unit 4.

• Analyzing structure word problem: pet store (1 of 2)
• Analyzing structure word problem: pet store (2 of 2)
• Combining mixtures example
• Rational equations word problem: combined rates
• Rational equations word problem: combined rates (example 2)

Mixtures and combined rates word problems

• Rational equations word problem: eliminating solutions
• Reasoning about unknown variables
• Reasoning about unknown variables: divisibility
• Structure in rational expression
• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.5: Solve Mixture Applications with Systems of Equations

• Last updated
• Save as PDF
• Page ID 30527

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Solve mixture applications
• Solve interest applications

Before you get started, take this readiness quiz.

• Multiply 4.025(1,562). If you missed this problem, review Example 1.8.22 .
• Write 8.2% as a decimal. If you missed this problem, review Example 1.8.46 .
• Earl’s dinner bill came to $32.50 and he wanted to leave an 18% tip. How much should the tip be? If you missed this problem, review Example 3.2.10 .

Solve Mixture Applications

When we solved mixture applications with coins and tickets earlier, we started by creating a table so we could organize the information. For a coin example with nickels and dimes, the table looked like this:

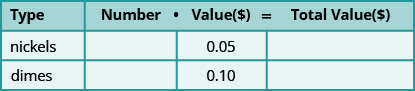
Using one variable meant that we had to relate the number of nickels and the number of dimes. We had to decide if we were going to let n be the number of nickels and then write the number of dimes in terms of n , or if we would let d be the number of dimes and write the number of nickels in terms of d .

Now that we know how to solve systems of equations with two variables, we’ll just let n be the number of nickels and d be the number of dimes. We’ll write one equation based on the total value column, like we did before, and the other equation will come from the number column.

For the first example, we’ll do a ticket problem where the ticket prices are in whole dollars, so we won’t need to use decimals just yet.

Example \(\PageIndex{1}\)

Translate to a system of equations and solve:

The box office at a movie theater sold 147 tickets for the evening show, and receipts totaled $1,302. How many $11 adult and how many $8 child tickets were sold?

Try It \(\PageIndex{2}\)

The ticket office at the zoo sold 553 tickets one day. The receipts totaled $3,936. How many $9 adult tickets and how many $6 child tickets were sold?

There were 206 adult tickets sold and 347 children tickets sold.

Try It \(\PageIndex{3}\)

A science center sold 1,363 tickets on a busy weekend. The receipts totaled $12,146. How many $12 adult tickets and how many $7 child tickets were sold?

There were 521 adult tickets sold and 842 children tickets sold.

In Example \(\PageIndex{4}\) we’ll solve a coin problem. Now that we know how to work with systems of two variables, naming the variables in the ‘number’ column will be easy.

Example \(\PageIndex{4}\)

Priam has a collection of nickels and quarters, with a total value of $7.30. The number of nickels is six less than three times the number of quarters. How many nickels and how many quarters does he have?

Try It \(\PageIndex{5}\)

Matilda has a handful of quarters and dimes, with a total value of $8.55. The number of quarters is 3 more than twice the number of dimes. How many dimes and how many quarters does she have?

Matilda has 13 dimes and 29 quarters.

Try It \(\PageIndex{6}\)

Juan has a pocketful of nickels and dimes. The total value of the coins is $8.10. The number of dimes is 9 less than twice the number of nickels. How many nickels and how many dimes does Juan have?

Juan has 36 nickels and 63 dimes.

Some mixture applications involve combining foods or drinks. Example situations might include combining raisins and nuts to make a trail mix or using two types of coffee beans to make a blend.

Example \(\PageIndex{7}\)

Carson wants to make 20 pounds of trail mix using nuts and chocolate chips. His budget requires that the trail mix costs him $7.60 per pound. Nuts cost $9.00 per pound and chocolate chips cost $2.00 per pound. How many pounds of nuts and how many pounds of chocolate chips should he use?

Try It \(\PageIndex{8}\)

Greta wants to make 5 pounds of a nut mix using peanuts and cashews. Her budget requires the mixture to cost her $6 per pound. Peanuts are $4 per pound and cashews are $9 per pound. How many pounds of peanuts and how many pounds of cashews should she use?

Greta should use 3 pounds of peanuts and 2 pounds of cashews.

Try It \(\PageIndex{9}\)

Sammy has most of the ingredients he needs to make a large batch of chili. The only items he lacks are beans and ground beef. He needs a total of 20 pounds combined of beans and ground beef and has a budget of $3 per pound. The price of beans is $1 per pound and the price of ground beef is $5 per pound. How many pounds of beans and how many pounds of ground beef should he purchase?

Sammy should purchase 10 pounds of beans and 10 pounds of ground beef.

Another application of mixture problems relates to concentrated cleaning supplies, other chemicals, and mixed drinks. The concentration is given as a percent. For example, a 20% concentrated household cleanser means that 20% of the total amount is cleanser, and the rest is water. To make 35 ounces of a 20% concentration, you mix 7 ounces (20% of 35) of the cleanser with 28 ounces of water.

For these kinds of mixture problems, we’ll use percent instead of value for one of the columns in our table.

Example \(\PageIndex{10}\)

Sasheena is a lab assistant at her community college. She needs to make 200 milliliters of a 40% solution of sulfuric acid for a lab experiment. The lab has only 25% and 50% solutions in the storeroom. How much should she mix of the 25% and the 50% solutions to make the 40% solution?

Try It \(\PageIndex{11}\)

LeBron needs 150 milliliters of a 30% solution of sulfuric acid for a lab experiment but only has access to a 25% and a 50% solution. How much of the 25% and how much of the 50% solution should he mix to make the 30% solution?

LeBron needs 120 ml of the 25% solution and 30 ml of the 50% solution.

Try It \(\PageIndex{12}\)

Anatole needs to make 250 milliliters of a 25% solution of hydrochloric acid for a lab experiment. The lab only has a 10% solution and a 40% solution in the storeroom. How much of the 10% and how much of the 40% solutions should he mix to make the 25% solution?

Anatole should mix 125 ml of the 10% solution and 125 ml of the 40% solution.

Solve Interest Applications

The formula to model interest applications is I = Prt . Interest, I , is the product of the principal, P , the rate, r , and the time, t . In our work here, we will calculate the interest earned in one year, so t will be 1.

We modify the column titles in the mixture table to show the formula for interest, as you’ll see in Example \(\PageIndex{13}\).

Example \(\PageIndex{13}\)

Adnan has $40,000 to invest and hopes to earn 7.1% interest per year. He will put some of the money into a stock fund that earns 8% per year and the rest into bonds that earns 3% per year. How much money should he put into each fund?

Try It \(\PageIndex{14}\)

Leon had $50,000 to invest and hopes to earn 6.2 % interest per year. He will put some of the money into a stock fund that earns 7% per year and the rest in to a savings account that earns 2% per year. How much money should he put into each fund?

Leon should put $42,000 in the stock fund and $8000 in the savings account.

Try It \(\PageIndex{15}\)

Julius invested $7,000 into two stock investments. One stock paid 11% interest and the other stock paid 13% interest. He earned 12.5% interest on the total investment. How much money did he put in each stock?

Julius invested $1,750 at 11% and $5,250 at 13%.

Example \(\PageIndex{16}\)

Rosie owes $21,540 on her two student loans. The interest rate on her bank loan is 10.5% and the interest rate on the federal loan is 5.9%. The total amount of interest she paid last year was $1,669.68. What was the principal for each loan?

Try It \(\PageIndex{17}\)

Laura owes $18,000 on her student loans. The interest rate on the bank loan is 2.5% and the interest rate on the federal loan is 6.9 %. The total amount of interest she paid last year was $1,066. What was the principal for each loan?

The principal amount for the bank loan was $4,000. The principal amount for the federal loan was $14,000.

Try It \(\PageIndex{18}\)

Jill’s Sandwich Shoppe owes $65,200 on two business loans, one at 4.5% interest and the other at 7.2% interest. The total amount of interest owed last year was $3,582. What was the principal for each loan?

The principal amount for was $41,200 at 4.5%. The principal amount was, $24,000 at 7.2%.

Access these online resources for additional instruction and practice with solving application problems with systems of linear equations.

• Cost and Mixture Word Problems
• Mixture Problems

Key Concepts

Please wait...

Mixture and Alligation – Concepts, Usage, and Tricks

Mixture and alligation problems are asked in almost every exam, whether it is Banking, SSC, Railways, or any other banking exams. In prelims or phase 1, word problems from this topic can be 2-3 while in mains concept of mixture and alligation can be asked in Data Interpretation and Data sufficiency as well.

Questions in this section are a bit tricky to solve and usually we apply the concepts and formulas of weighted average, percentages and ratios to solve such questions. But these questions can also be solved using the concept of alligation and in this article we will discuss the detailed concept of mixture and alligation.

Register Here to Take A Free Mock Test Now

For Free Practice Questions on Mixture and Alligations Register here.

Understanding the Concept of Mixture and Alligation

Mixture: When two or more ingredients are mixed, mixtures can be of two types:

• Simple mixture: Formed after mixing two or more different ingredients.
• Complex mixture: Formed after mixing two or more different mixtures.

Rule of Alligation

The rule enables us to find the ratio in which two or more ingredients/mixture of different prices/concentration are mixed together to form a final mixture or desired price or concentration. Two methods are used:

Method 1 (formula method): It is given as-

Method 2 (Diagram method): The above method can be expressed using a diagram which will be more convenient to understand-

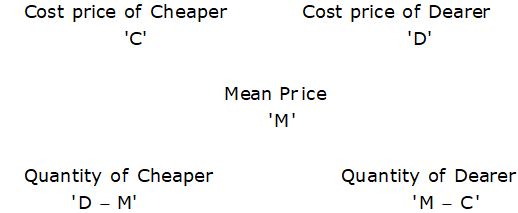
This rule of allegation can be applied to other topics such as profit and loss, average, percentage, simple interest/compound interest, ratio, and proportion .

Register here for free Study Material PDFs .

Alligation in Mixture Problems

We will see how the rule of allegation can be applied in mixture problems-

Example 1: A shopkeeper mixes 30 kg of type A rice of Rs.40/kg and 45 kg of type B rice of Rs.30/kg, then find the price of formed mixture of rice.

By the rule of alligation:

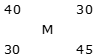
(30 – M): (M – 40) = 30: 45 = 2: 3

90 – 3M = 2M – 80

Hence, price of mixture = Rs.34/kg

Note: After applying the concept of alligation on the price of the item of concentration of mixture we will get the ratio in which these two items or mixture are mixed.

Example 2: Mixture A of milk and water contains 75% milk and mixture B of milk and water contains 10% water, then find the ratio in which these two mixtures are mixed to form a third mixture which contains 15% water in it.

Water percent in mixture A = 100% – 75% of 25%

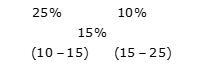
Required ratio = -5: -10

Be exam ready with our Math Coach Feature – Try it for Free Here

Read Here to Find Tips and Tricks to Increase your Calculation Speed

Alligation in Profit and Loss Problems

It is used to find the overall profit or loss percent when cost prices of two items and profit/loss percent on the items are given-

Example 3: A shopkeeper sells type A rice at 20% profit and type B rice at 15% loss. If overall he earns 13% profit, then find the cost price of type A rice to type B rice.

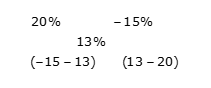
The ratio of the cost price of type A to type B rice = -28: -7

Note: After applying alligatiion concept in profit/loss percent earned on the items we will get the ratio of cost prices of the items.

Put ‘–’ sign when loss percent is given .

Example 4: A shopkeeper purchased a table for Rs.1200 and sold it at 20% profit, he purchased a chair at Rs.400 and sold it at 10% profit, the find the overall profit percent earned by him.

Let overall profit percent = M%

(10 – M): (M – 20) = 1200: 400 = 3: 1

10 – M = 3M – 60

Hence, overall profit percent = M = 17.5%

Register here for FREE Study Material and Practice Questions PDFs .

Alligation in Speed, distance, and Time Problems

The concept of mixture and alligation can be used to find the average speed of journey-

Example 5: A person covers the first 3 hours of a journey with a speed 80 km/h and the remaining 5 hours with a speed 56 km/h, then find his average speed of the journey.

Let average speed = X

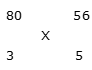
(56 – X): (X – 80) = 3: 5

280 – 5X = 3X – 240

Average speed of journey = 65 km/h

Note: After applying the concept of alligation on speed on different parts of the journey we will get the ratio of time taken to cover those parts.

Example 6: A distance of 360 km can be covered in 6 hours when some part of the journey is covered with speed 45 km/h and remaining with speed 90 km/h, then find the distance covered with speed 45 km/h.

Average speed of the journey = 360/6 = 60 km/h

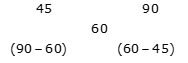
Ratio of time taken = 30: 15 = 2: 1

Time for which journey is covered with speed 45 km/h = 6 * (2/3) = 4 hours

Distance covered by 45 km/h speed = 45 * 4 = 180 km

Attempt a FREE RRB NTPC Mock Here

Alligation in Simple/Compound Interest Problems

The concept of alligation can be applied to SI and CI if we can calculate the effective interest rate for given time period.

For example:

Equivalent of 20% SI for 3 years = 20% * 3 = 60%

Equivalent of 20% CI for 2 years = [(1.2) 2 – 1] * 100 = 44%

Example 7: Rahul lent Rs.5000 to Sumit at 25% SI for 2 years and borrowed Rs.3000 from Suresh for 3 years 10% SI, then find the profit/loss on interest amount of Rahul.

Effective rate of interest for 2 years on lent amount = 25% * 2 = 50%

Effective rate of interest for 3 years on borrowed amount = -10% * 3 = -30% [Negative because interest will be given.]

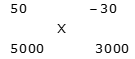
(-30 – X): (X – 50) = 5000: 3000 = 5: 3

-90 – 3X = 5X – 250

Hence, total profit on interest amount = 20% of (5000 + 3000) =

Note: After applying the alligation concept in effective interest rate we will get the ratio of amount invested.

Example 8: Ronit invested a certain amount in scheme A for 2 years at 10% annual CI and the remaining amount in scheme B for 3 years at 20% annual CI. If the total interest amount received by him is 41.72% of the total invested amount, then find the ratio of the invested amount in scheme A to that in scheme B.

Effective interest rate for 2 years on scheme A = [(1.1) 2 – 1] * 100 = 21%

Effective interest rate for 3 years on scheme B = [(1.2) 3 – 1] * 100 = 72.8%

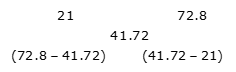
Ratio of amount invested in scheme A to B = 31.08: 20.72

Alligation in Average, Ratio, and Percentage Problems

By applying the rule of alligation we can solve the problems of averages, ratios, and percentages quickly.

Example: 9: Average age of a 25 students of a class is 24 years and average age of remaining 15 students of the class is 18 years, then find the average age of the class.

Let average age of class = A

(18 – A): (A – 24) = 25: 15 = 5: 3

54 – 3A = 5A – 120

Hence, average age of the class = A = 21.75 years

Example 10: Ratio of marks obtained to maximum marks by Arun in math and English is 5: 3 and 3: 1. If maximum marks in both the subjects are same, then find the ratio of marks obtained to maximum marks by Arun when both the subjects are taken together.

(3/4 – A): (A – 5/8) = 1: 1

3/4 – A = A – 5/8

Required ratio = 11: (16 – 11) = 11: 5

Example 11: In states A and B out of the total population, the male population is 60% and 50% respectively. If the male population, when both the states are taken together, becomes 58% of the total population, then find that total population of state B is what percent of that of state A.

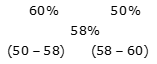
Ratio of total population of state A to that of state B = -8: -2 = 4: 1

Required percent = (1/4) * 100

We hope you have got an idea of the topic and can start practicing questions of mixture and alligation.

Stay connected for more topics.

All the best.

Some Useful Links

For Free Practice Questions Register here.

For High-Level DI Questions, Register here.

Solve DI based on Time and Work Here

How to Master Quants section – Know Here!

Attempt Various Free Mock Tests Here: Topic Tests, Sectional Tests, and Full Mock Tests.

Study at your own convenience anywhere. Download the Oliveboard app now!

Oliveboard is a learning & practice platform for premier entrance exams. We have helped over 1 crore users since 2012 with their Bank, SSC, Railways, Insurance, Teaching and other competitive Exams preparation.

  Oliveboard Live Courses & Mock Test Series

• Download IFSCA Grade A PYQs
• Download SEBI Grade A PYQs
• Download SEBI Grade A 300+ MCQs
• Download 500+ Free Ebooks for Govt. Exams Preparations
• Attempt Free SSC CGL Mock Test 2024
• Attempt Free IBPS Mock Test 2024
• Attempt Free SSC CHSL Mock Test 2024
• Download Oliveboard App
• Follow Us on Google News for Latest Update
• Join Telegram Group for Latest Govt Jobs Update

Leave a comment Cancel reply

Download 500+ Free Ebooks (Limited Offer)👉👉

Thank You 🙌

• IBPS RRB Exam 2023 - Free Course
• Current Affairs
• General Knowledge
• SSC CGL Pre.Yrs.Papers
• SSC CGL Practice Papers
• SBI Clerk PYQ
• IBPS PO PYQ
• IBPS Clerk PYQ
• SBI PO Practice Paper
• IBPS Clerk Syllabus of Quantitative Aptitude

Ratio & Proportion, Percentage

• Ratios and Percentages
• Ratio and Proportion
• Tricks To Solve Ratio and Proportion
• Tips & Tricks To Solve Ratio & Proportion - Advance Level
• Basic Concept of Percentage
• Percentages
• Average in Maths
• Tricks To Solve Questions On Average
• Time and Work - Aptitude Questions and Answers

Time Speed, and Distance

• Time Speed Distance
• Speed and Distance Advance Level

Mixtures & Allegations

• Alligation or Mixture - Aptitude Questions and Answers

Tricks To Solve Mixture and Alligation

• Mixtures and Alligation
• Mixture and Alligation | Set 2

Partnership

• Introduction to Accounting for Partnership
• Partnership : Definition, Concepts, Types of Partnership
• Partnership | Meaning and Features of Partnership
• Types of Partnership
• Tricks To Solve Partnership Problems
• Surface Areas and Volumes

Bar Graphs, Linear Graphs and Pie Charts

• Bar Graphs and Histograms
• What is Linear Graph? Definition, Equation, Examples

Trigonometry, Height and Distances

• Trigonometry & Height and Distances
• Practice Set For Height & Distance
• Height and Distance
• Trigonometric Ratios
• Trigonometry in Maths: Table, Formulas, Identities and Ratios
• Laws of Logarithms
• Logarithm Formula
• Permutation and Combination
• Permutations and Combinations
• Combinations Formula with Examples
• Permutation
• Linear Equations Formula
• Linear Equations in One Variable
• Linear Equation in Two Variables
• Pair of Linear Equations in Two Variables
• Relationship Between Two Variables
• Algebraic Methods of Solving Pair of Linear Equations in Two Variables
• Linear Function
• Solve the Linear Equation using Substitution Method
• Quadratic Equations - Roots, Solution, Formula and Examples
• Solving Quadratic Equations
• Quadratic Formula
• Roots of Quadratic Equation

Profit, Loss, and Discount

• Practice Set For Profit and Loss
• Profit and Loss

Mensuration

• Mensuration 2D
• Mensuration in Maths | Formulas for 2D and 3D Shapes, Examples
• Practice Question On Area And Perimeter Of All Shapes
• Algebra in Math: Definition, Branches, Basics and Examples
• Data Interpretation
• Cumulative DI For Bank PO Exam
• DI Table Graph and Chart Questions For Bank PO Exams

Miscellaneous

• Approximation - Aptitude Question and Answers
• Arithmetic Progression
• Number Series Reasoning Questions and Answers
• Important Formulas of Interest, Mensuration, Permutation & Combination and Probability
• Basic Concept Of Number System
• Basic Concepts Of Whole Numbers

Mixture and alligation are one of the most important and intrinsic topics for SSC CGL. As it is not an individual chapter, it is a method of solving problems of different topics like ratio, profit, loss, average, etc. Almost 3-4 questions are asked in the prelims exam that can be solved using the technique of allegation. In this article we will be studying the method of the allegation and how can we implement it for solving questions of various topics in a much easier and smarter way.

Let’s start with the basic definition first:-

Mixture : It is the process of mixing two or more elements/ingredients together.

Allegation : It is a process or a rule that tells us how to mix two or more ingredients/mixtures to get the desired mixture of a certain price & concentration.

Now there are 2 ways of applying the allegation technique to questions.

Formula Method:

Quantity of cheaper/ Quantity of dearer = (Price of dearer – Mean price)/ (Mean Price- Price of cheaper)

Diagram Method:

The above-mentioned formula can be better understood using the diagram method & it is more convenient to use this method. 

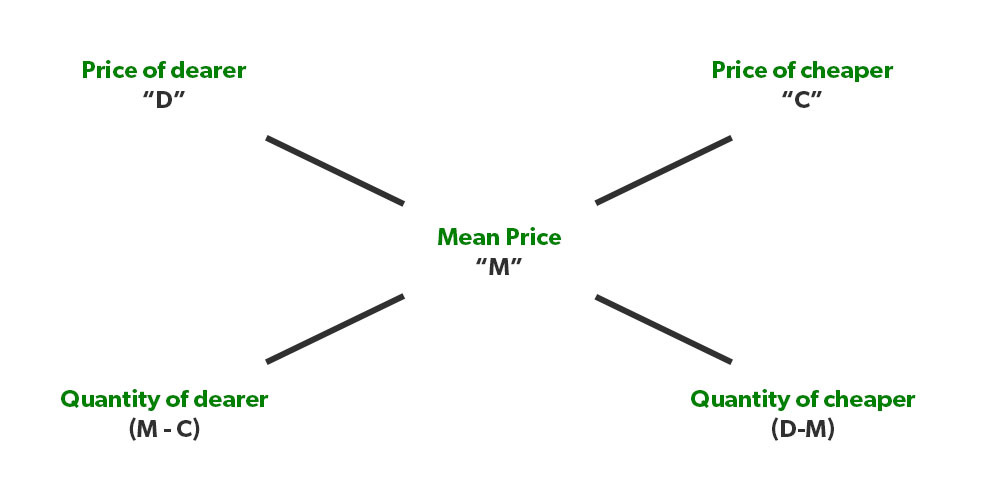
Note 1. Please note that allegation is a concept with the help of which we can find the mean price if 2 or more ingredients are mixed in some ratio or we can also find the ratio in which two or more items should be mixed to get a certain price or concentration of the mixture.   

Note 2.  (d-m)/(m-c) is nothing but the ratio of quantities of both the items, so even if we are given a ratio in which 2 items are mixed, we can find the “m”..

Now let’s try to solve a variety of problems using the allegation method which will help you in understanding the concept in a much better way.

Illustration 1. If 20 kgs of rice which cost 45 Rs/Kg is mixed with 25 kgs of rice which costs 30 Rs/Kg. What will be the price of the final mixture?

Solution: In this question, we have to find “M”

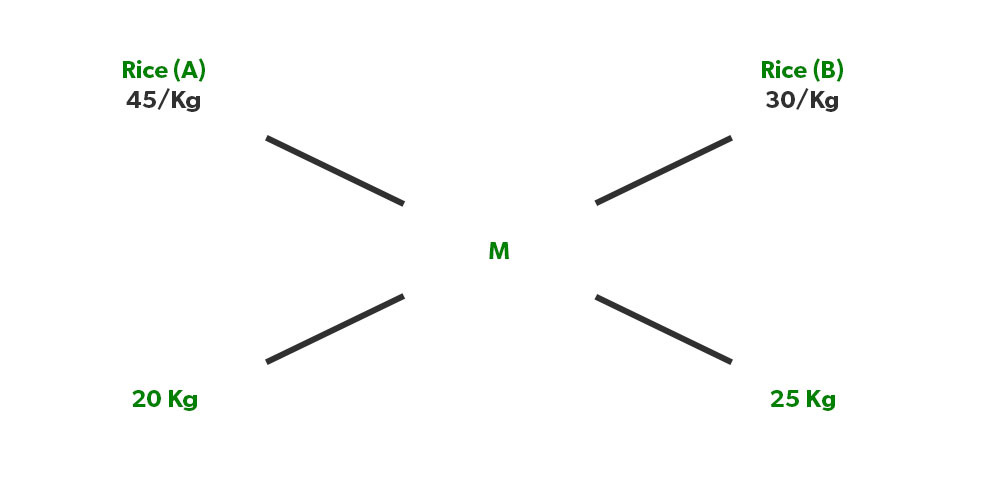
Now as we know, (45-M)/(M-30)=25/20

⇒ (45-M)/(M-30)= 5/4

⇒180-4M = 5M- 150

⇒ M= 330/9= 36.6 Rs/Kg

Illustration 2. Oranges of type A that cost 60 Rs/Kg is mixed with the orange of type B that costs 80 Rs/Kg in a ratio of 3:5. What will be the price of the resultant mixture of oranges?

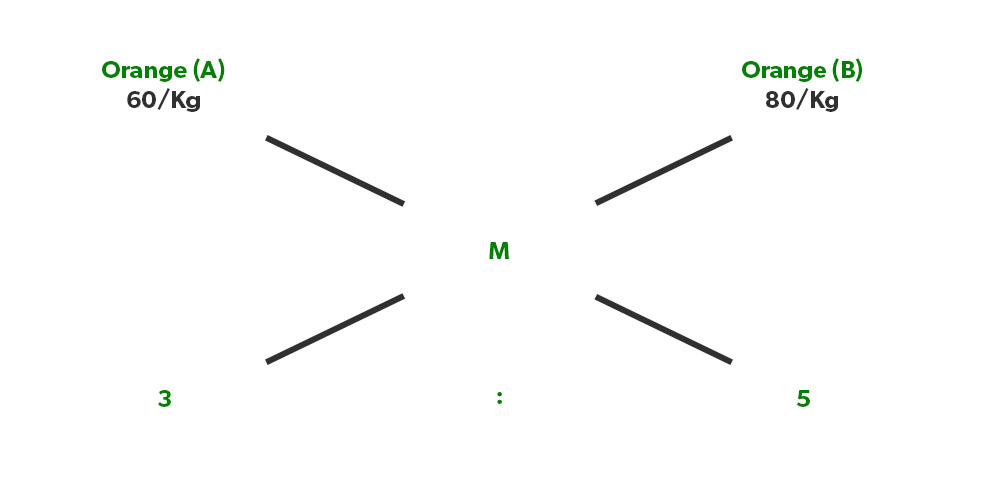
Solution: Again applying the same formula,

(60-M)/(M-80)= 5/3

180-3M = 5M-400

M= 580/8= 72.5 Rs

Illustration 3. If rice or 45 Rs/kg is mixed with rice of 35 Rs/kg and the price of the resultant mixture is 42.5 Rs/kg. What is the ratio that they were mixed in?

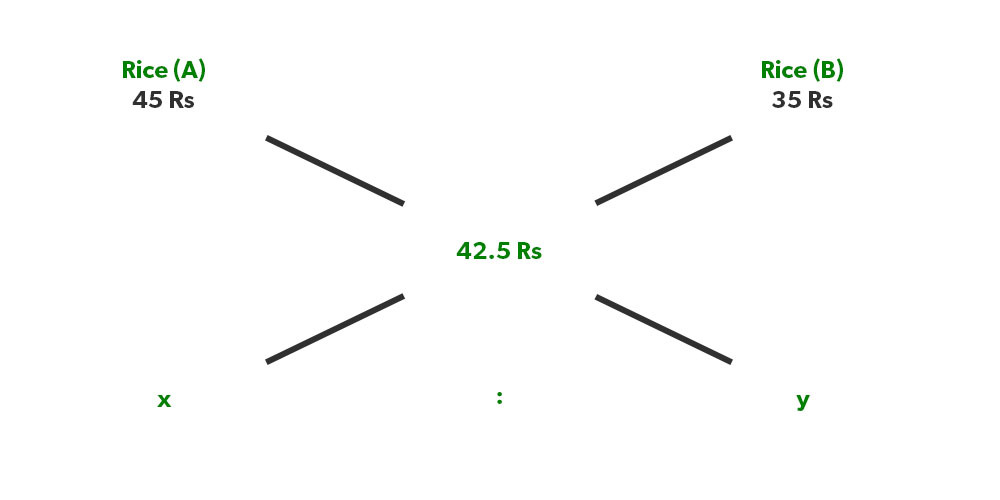
Solution: As we know, (45-42.5)/(42.5-35) = Y/X

2.5/7.5= Y/X

1/3 = Y/X, hence they were mixed in the ratio of 3:1.

Illustration 4. Mixture A which contains 30% water is mixed with Mixture B which has 20% water in a ratio of 2:5. What will be the % of water in the resultant mixture?

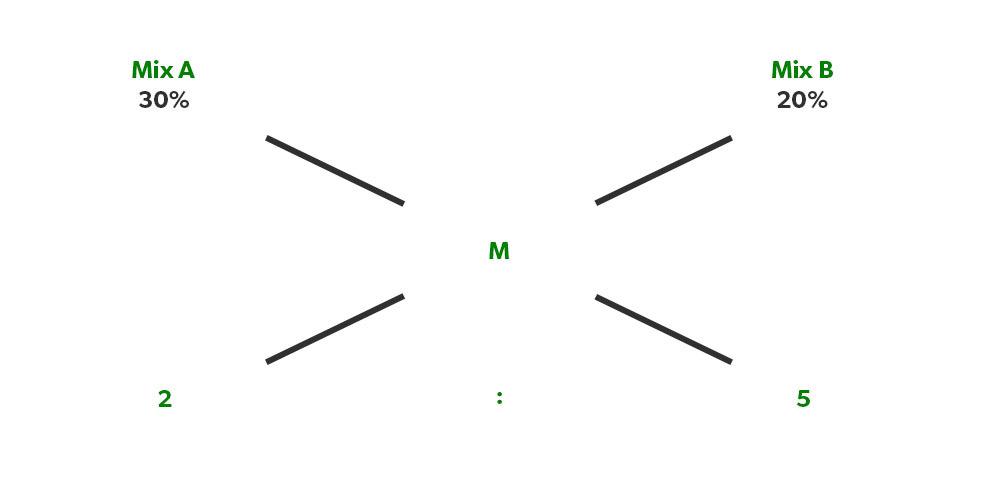
Solution: Allegation can also be applied to percentages & not just absolute values.

(30%-M)/(M-20%)= 5/2

60% – 2M= 5M – 100%

M = 160%/7 = 22.8%

Illustration 5. A shopkeeper sells one item at 20% profit and another item at 5% profit. If the overall profit of the shopkeeper is 10 per cent. What is the ratio of the CP of item A to item B?

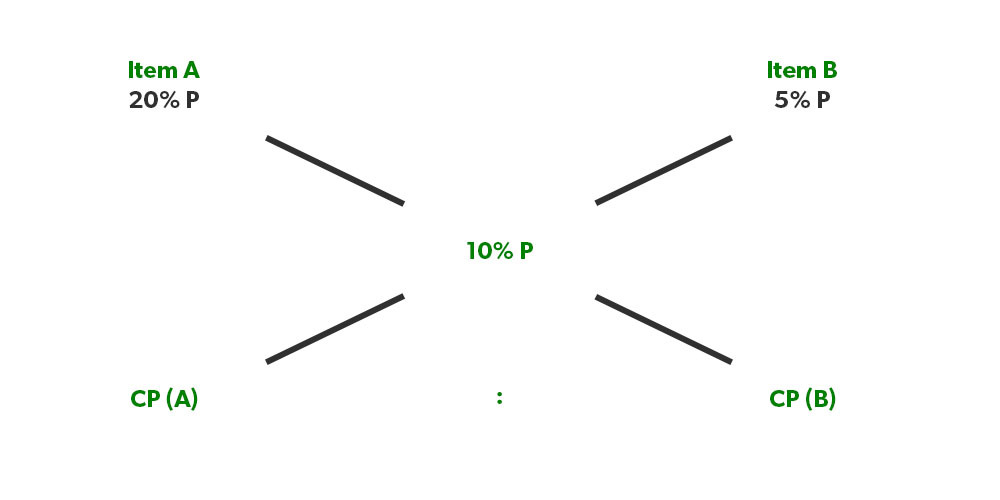
Solution: Here, the ratio of quantities will give us ratio of the cost price

So, (20%-10%)/ (10%-5%)= CP (B)/CP (A)

 10%/5%= CP (B)/ CP (A)

1:2 = CP (A)/ CP(B)

Illustration 6. A shopkeeper sells Type A rice at 40 Rs/Kg and types B rice at 60 Rs/kg. If he wants to gain a profit of 10% after selling the mixture of both types in the ratio Of 2:3. What should be the selling price of the mixture?

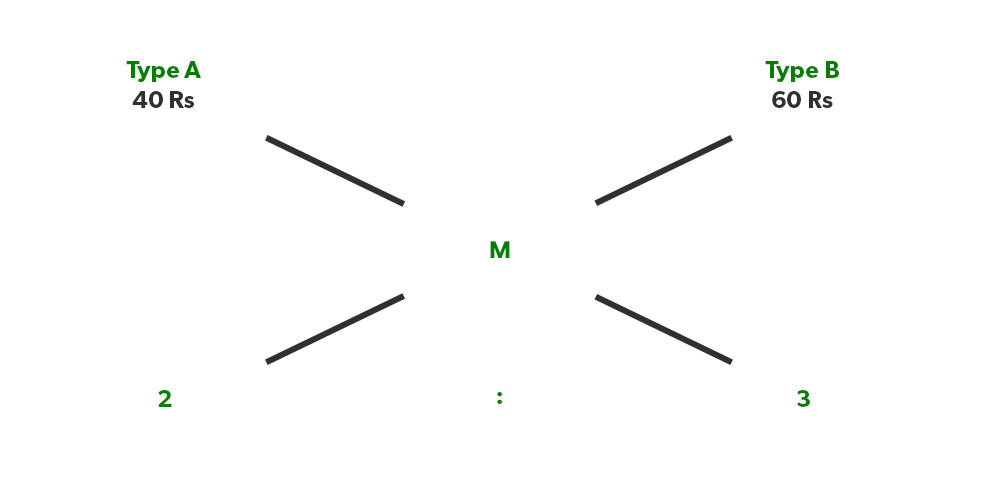
Solution: Here the value of M will give us no profit no loss amount.  (40-M)/(M-60)= 3/2

It gives us M= 260/5 = 52 

Now to get a profit of 10 %, the shopkeeper has to sell it at, (52) × (110/100) = 57.2 Rs

Illustration 7. If a shopkeeper sells an item of 2000 Rs at 15 per cent profit & another item of 3500 Rs at 5 per cent loss. Find his overall profit/loss percentage?

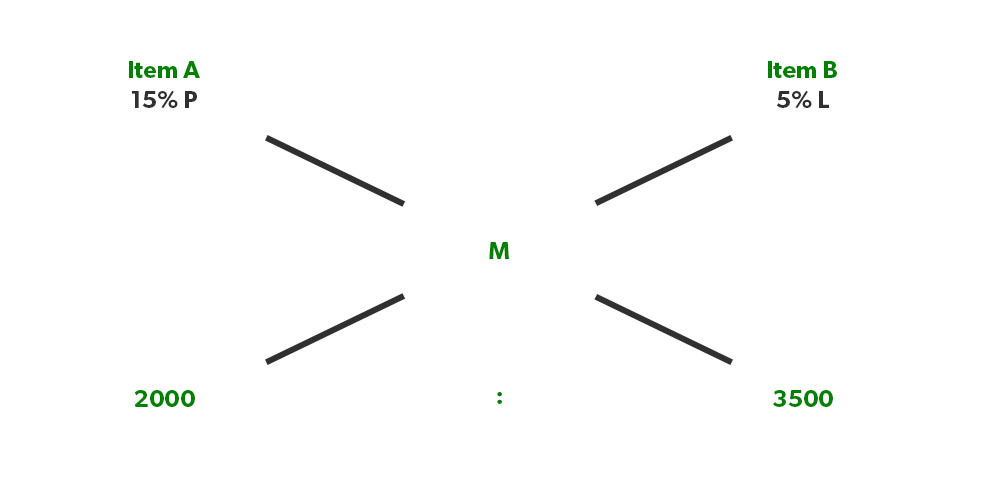
Solution: We will take loss % with minus sign,

(15% – M)/ (M- (-5%) = 7/4

It gives us M = 2.27%

Illustration 8. If the average marks of boys in a class is 75 and the average marks of girls in that class is 80. If the ratio of boys to girls in that class is 4:3. Find the average marks of the class?

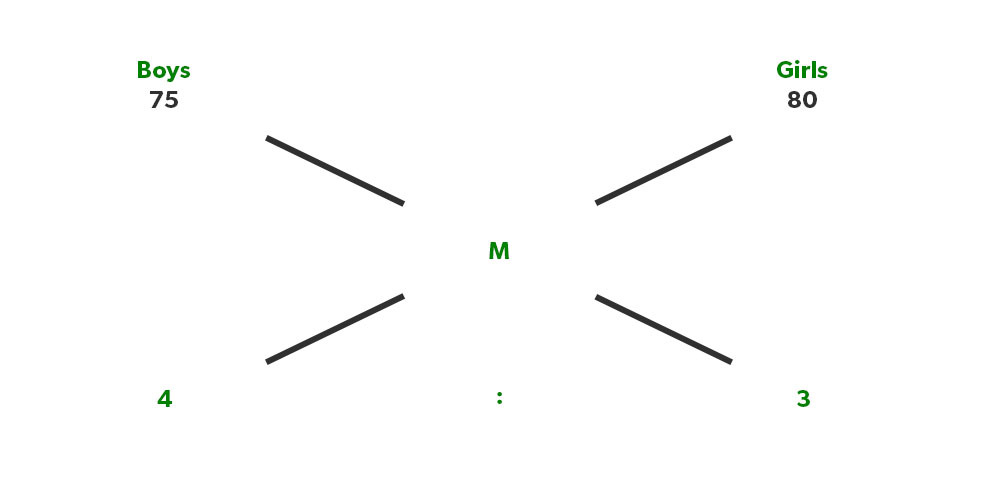
Solution: Here also, we can find the average of the whole class easily,

(75-M)/( M-80)= 3/4

Illustration 9. If a shopkeeper sold a mixture of mangoes at 100 Rs/Kg in which he mixed 2 types of mangoes that cost him 50 Rs/Kg and 75 Rs/Kg in the ratios of 2:3 respectively. What is the profit percentage of the shopkeeper?

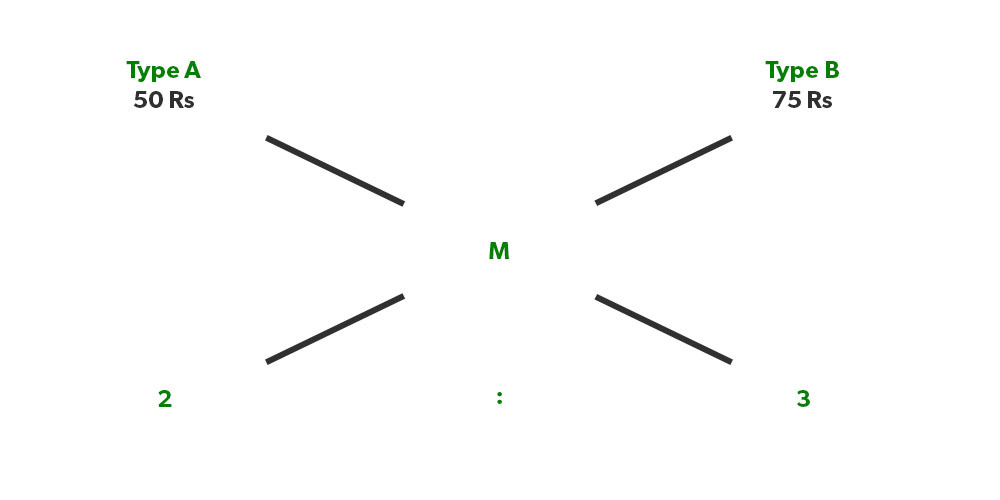
Solution: (50-M)/( M-75)= 3/2

M= 65 Rs/kg

Now he sold this at 100 Rs/Kg, so his profit is (35/65)× 100 = 53.8 % P

Illustration 10.  If a cyclist covered 3/5th distance or the track with 15 km/hr and the rest of the distance with 10km/her. What is the average speed of the cyclist?

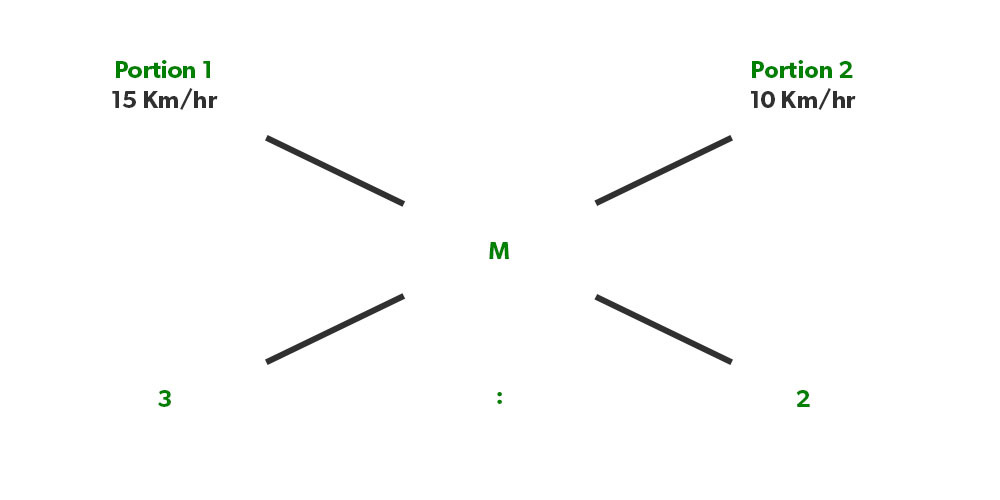
Solution: (15-M)/(M-10)= 2/3

M= 13 km/Hr

Illustration 11. In a village, the average age of males is 35 years & in another village, the average age of males is 30 years. If the ratio of the total number of females in both the villages is 2:3. Find the average age if both the villages are combined?

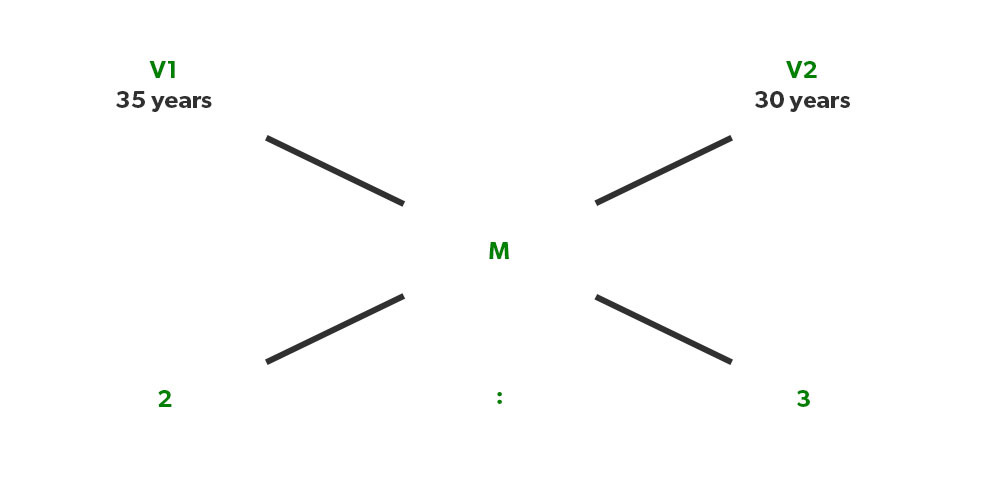
Solution: Average age will be, (35-M)/ (M-30)= 3/2

That gives us M= 36 Years

Illustration 12. A lender gives money at 8% SI for 2 years to a guy & takes money from somewhere at 5% SI for 3 years. If the amount he lent to the amount he took is in the ratio of 3:4. Find his overall profit/loss %?

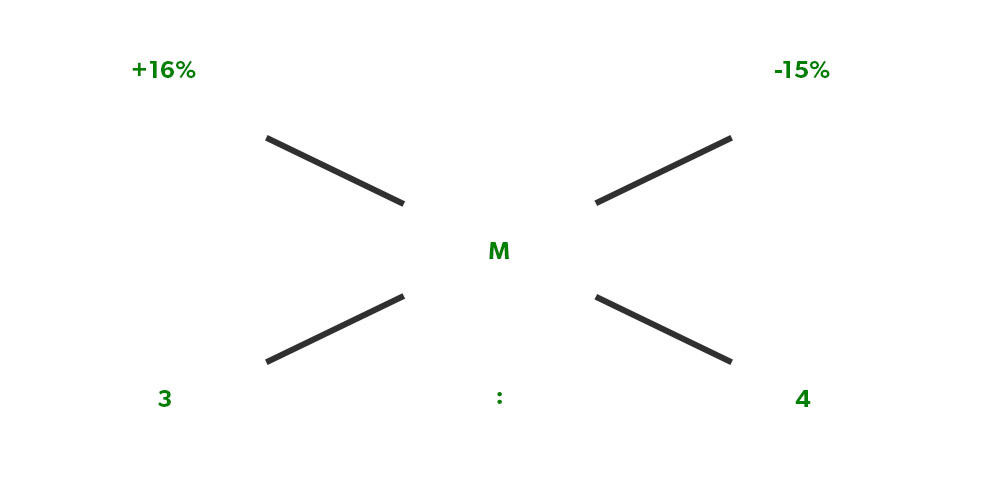
Solution: 8% for 2 years SI becomes 16% & 5% for 3 years SI becomes 15%.  

overall profit/loss % will be, (16%- M)/ (M+15%)= 4/3

That gives us M= -12/7% = loss of 12/7%

Illustration 13. If a racer can finish a track in 10 hours & another racer can finish the same track in 15 hours. If both are supposed to take part in the relay race & racer 1 has to run the 2/5th part of the track. How long will it take for both of them to complete the race?

Solution: If racer 1 is covering 2/5th of the track, hence racer 2 will cover 3/5th of the track.

Applying the rule of the allegation, we get

(10 Hrs – M)/ (M-15 Hrs)= 3/2

This gives us, M= 13 Hrs

Illustration 14. A shopkeeper mixes water in milk If he mixes 1-litre water in 5-litre milk & the actual cost of milk is 30Rs/Litre but he sells the milk at 28 Rs/litre. Find his actual profit or loss?

Solution: The key concept here to understand is that water costs zero rupees.

Hence the no profit no loss value of the mixture is, 

(30-M)/ (M-0)= 1/5

That gives us M= 25 Rs.

Now he sells this at 28 Rs, so profit % is (3/25) × 100 = 12%

Illustration 15. A guy who works at a juice centre mixes water with juice in a ratio of 5:1 respectively. If the actual price of fruits is 50 Rs/glass & he sells 60 Rs/glass. find his actual profit/glass?

Solution: Again, repeating the same logic

(50-M)/ (M-0)= 1/5 

M= 250/6 Rs, so his profit % is [60- (250/6)]/ (250/6) × 100 = 44%

This was some illustration to help you understand the application of Mixture & Allegation. 

Please Login to comment...

Similar reads.

• Banking Quantitative Aptitude
• SSC Quantitative Aptitude
• SSC/Banking

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Facility for Rare Isotope Beams

At michigan state university, international research team uses wavefunction matching to solve quantum many-body problems, new approach makes calculations with realistic interactions possible.

FRIB researchers are part of an international research team solving challenging computational problems in quantum physics using a new method called wavefunction matching. The new approach has applications to fields such as nuclear physics, where it is enabling theoretical calculations of atomic nuclei that were previously not possible. The details are published in Nature (“Wavefunction matching for solving quantum many-body problems”) .

Ab initio methods and their computational challenges

An ab initio method describes a complex system by starting from a description of its elementary components and their interactions. For the case of nuclear physics, the elementary components are protons and neutrons. Some key questions that ab initio calculations can help address are the binding energies and properties of atomic nuclei not yet observed and linking nuclear structure to the underlying interactions among protons and neutrons.

Yet, some ab initio methods struggle to produce reliable calculations for systems with complex interactions. One such method is quantum Monte Carlo simulations. In quantum Monte Carlo simulations, quantities are computed using random or stochastic processes. While quantum Monte Carlo simulations can be efficient and powerful, they have a significant weakness: the sign problem. The sign problem develops when positive and negative weight contributions cancel each other out. This cancellation results in inaccurate final predictions. It is often the case that quantum Monte Carlo simulations can be performed for an approximate or simplified interaction, but the corresponding simulations for realistic interactions produce severe sign problems and are therefore not possible.

Using ‘plastic surgery’ to make calculations possible

The new wavefunction-matching approach is designed to solve such computational problems. The research team—from Gaziantep Islam Science and Technology University in Turkey; University of Bonn, Ruhr University Bochum, and Forschungszentrum Jülich in Germany; Institute for Basic Science in South Korea; South China Normal University, Sun Yat-Sen University, and Graduate School of China Academy of Engineering Physics in China; Tbilisi State University in Georgia; CEA Paris-Saclay and Université Paris-Saclay in France; and Mississippi State University and the Facility for Rare Isotope Beams (FRIB) at Michigan State University (MSU)—includes  Dean Lee , professor of physics at FRIB and in MSU’s Department of Physics and Astronomy and head of the Theoretical Nuclear Science department at FRIB, and  Yuan-Zhuo Ma , postdoctoral research associate at FRIB.

“We are often faced with the situation that we can perform calculations using a simple approximate interaction, but realistic high-fidelity interactions cause severe computational problems,” said Lee. “Wavefunction matching solves this problem by doing plastic surgery. It removes the short-distance part of the high-fidelity interaction, and replaces it with the short-distance part of an easily computable interaction.”

This transformation is done in a way that preserves all of the important properties of the original realistic interaction. Since the new wavefunctions look similar to that of the easily computable interaction, researchers can now perform calculations using the easily computable interaction and apply a standard procedure for handling small corrections called perturbation theory.  A team effort

The research team applied this new method to lattice quantum Monte Carlo simulations for light nuclei, medium-mass nuclei, neutron matter, and nuclear matter. Using precise ab initio calculations, the results closely matched real-world data on nuclear properties such as size, structure, and binding energies. Calculations that were once impossible due to the sign problem can now be performed using wavefunction matching.

“It is a fantastic project and an excellent opportunity to work with the brightest nuclear scientist s in FRIB and around the globe,” said Ma. “As a theorist , I'm also very excited about programming and conducting research on the world's most powerful exascale supercomputers, such as Frontier , which allows us to implement wavefunction matching to explore the mysteries of nuclear physics.”

While the research team focused solely on quantum Monte Carlo simulations, wavefunction matching should be useful for many different ab initio approaches, including both classical and  quantum computing calculations. The researchers at FRIB worked with collaborators at institutions in China, France, Germany, South Korea, Turkey, and United States.

“The work is the culmination of effort over many years to handle the computational problems associated with realistic high-fidelity nuclear interactions,” said Lee. “It is very satisfying to see that the computational problems are cleanly resolved with this new approach. We are grateful to all of the collaboration members who contributed to this project, in particular, the lead author, Serdar Elhatisari.”

This material is based upon work supported by the U.S. Department of Energy, the U.S. National Science Foundation, the German Research Foundation, the National Natural Science Foundation of China, the Chinese Academy of Sciences President’s International Fellowship Initiative, Volkswagen Stiftung, the European Research Council, the Scientific and Technological Research Council of Turkey, the National Natural Science Foundation of China, the National Security Academic Fund, the Rare Isotope Science Project of the Institute for Basic Science, the National Research Foundation of Korea, the Institute for Basic Science, and the Espace de Structure et de réactions Nucléaires Théorique.

Michigan State University operates the Facility for Rare Isotope Beams (FRIB) as a user facility for the U.S. Department of Energy Office of Science (DOE-SC), supporting the mission of the DOE-SC Office of Nuclear Physics. Hosting what is designed to be the most powerful heavy-ion accelerator, FRIB enables scientists to make discoveries about the properties of rare isotopes in order to better understand the physics of nuclei, nuclear astrophysics, fundamental interactions, and applications for society, including in medicine, homeland security, and industry.

The U.S. Department of Energy Office of Science is the single largest supporter of basic research in the physical sciences in the United States and is working to address some of today’s most pressing challenges. For more information, visit energy.gov/science.