quadratic problem solving questions

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

6.1: Quadratic Equations (Exercises)

• Last updated
• Save as PDF
• Page ID 56066

For the following exercises, solve the quadratic equation by factoring.

40. \(2 x^{2}-7 x-4=0\) 41. \(3 x^{2}+18 x+15=0\) 42. \(25 x^{2}-9=0\) 43. \(7 x^{2}-9 x=0\)

For the following exercises, solve the quadratic equation by using the square-root property.

44. \(x^{2}=49\) 45. \((x-4)^{2}=36\)

For the following exercises, solve the quadratic equation by completing the square.

46. \(x^{2}+8 x-5=0\) 47. \(4 x^{2}+2 x-1=0\)

For the following exercises, solve the quadratic equation by using the quadratic formula. If the solutions are not real, state No real solution.

48. \(2 x^{2}-5 x+1=0\) 49. \(15 x^{2}-x-2=0\)

For the following exercises, solve the quadratic equation by the method of your choice.

50. \((x-2)^{2}=16\) 51. \(x^{2}=10 x+3\)

Quadratic Equations

An example of a Quadratic Equation :

The function can make nice curves like this one:

The name Quadratic comes from "quad" meaning square, because the variable gets squared (like x 2 ).

It is also called an "Equation of Degree 2" (because of the "2" on the x )

Standard Form

The Standard Form of a Quadratic Equation looks like this:

• a , b and c are known values. a can't be 0
• x is the variable or unknown (we don't know it yet)

Here are some examples:

Have a Play With It

Play with the Quadratic Equation Explorer so you can see:

• the function's graph, and
• the solutions (called "roots").

Hidden Quadratic Equations!

As we saw before, the Standard Form of a Quadratic Equation is

But sometimes a quadratic equation does not look like that!

For example:

How To Solve Them?

The " solutions " to the Quadratic Equation are where it is equal to zero .

They are also called " roots ", or sometimes " zeros "

There are usually 2 solutions (as shown in this graph).

And there are a few different ways to find the solutions:

Just plug in the values of a, b and c, and do the calculations.

We will look at this method in more detail now.

About the Quadratic Formula

First of all what is that plus/minus thing that looks like ± ?

The ± means there are TWO answers:

x = −b + √(b 2 − 4ac) 2a

x = −b − √(b 2 − 4ac) 2a

Here is an example with two answers:

But it does not always work out like that!

• Imagine if the curve "just touches" the x-axis.
• Or imagine the curve is so high it doesn't even cross the x-axis!

This is where the "Discriminant" helps us ...

Discriminant

Do you see b 2 − 4ac in the formula above? It is called the Discriminant , because it can "discriminate" between the possible types of answer:

• when b 2 − 4ac is positive, we get two Real solutions
• when it is zero we get just ONE real solution (both answers are the same)
• when it is negative we get a pair of Complex solutions

Complex solutions? Let's talk about them after we see how to use the formula.

Using the Quadratic Formula

Just put the values of a, b and c into the Quadratic Formula, and do the calculations.

Example: Solve 5x 2 + 6x + 1 = 0

Answer: x = −0.2 or x = −1

Let's check the answers:

Remembering The Formula

A kind reader suggested singing it to "Pop Goes the Weasel":

Try singing it a few times and it will get stuck in your head!

Or you can remember this story:

x = −b ± √(b 2 − 4ac) 2a

"A negative boy was thinking yes or no about going to a party, at the party he talked to a square boy but not to the 4 awesome chicks. It was all over at 2 am. "

Complex Solutions?

When the Discriminant (the value b 2 − 4ac ) is negative we get a pair of Complex solutions ... what does that mean?

It means our answer will include Imaginary Numbers . Wow!

Example: Solve 5x 2 + 2x + 1 = 0

Answer: x = −0.2 ± 0.4 i

The graph does not cross the x-axis. That is why we ended up with complex numbers.

In a way it is easier: we don't need more calculation, we leave it as −0.2 ± 0.4 i .

Example: Solve x 2 − 4x + 6.25 = 0

Answer: x = 2 ± 1.5 i

BUT an upside-down mirror image of our equation does cross the x-axis at 2 ± 1.5 (note: missing the i ).

Just an interesting fact for you!

• Quadratic Equation in Standard Form: ax 2 + bx + c = 0
• Quadratic Equations can be factored
• Quadratic Formula: x = −b ± √(b 2 − 4ac) 2a
• positive, there are 2 real solutions
• zero, there is one real solution
• negative, there are 2 complex solutions

Reset password New user? Sign up

Existing user? Log in

• Quadratic Equations

Concept Quizzes

• Quadratic Equations Warmup
• Distributive Property - Multiple Terms
• Multiplying Polynomials - Quadratics
• Quadratics - Factoring
• Solve by Quadratic Formula
• Quadratic Equations - Word Problems
• Quadratic Equations - Problem Solving

Challenge Quizzes

• Quadratic Equations: Level 2 Challenges
• Quadratic Equations: Level 3 Challenges
• Quadratic Equations: Level 4 Challenges
• Multiple Terms
• Factoring Quadratics

Problem Loading...

Note Loading...

Set Loading...

Solving Quadratic Equations: Worksheets with Answers

Whether you want a homework, some cover work, or a lovely bit of extra practise, this is the place for you. And best of all they all (well, most!) come with answers.

Mathster keyboard_arrow_up Back to Top

Mathster is a fantastic resource for creating online and paper-based assessments and homeworks. They have kindly allowed me to create 3 editable versions of each worksheet, complete with answers.

Corbett Maths keyboard_arrow_up Back to Top

Corbett Maths offers outstanding, original exam style questions on any topic, as well as videos, past papers and 5-a-day. It really is one of the very best websites around.

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

General Quadratic Word Problems

Projectiles General Word Problems Max/Min Problems

Most quadratic word problems should seem very familiar, as they are built from the linear problems that you've done in the past. You will need to use keywords to interpret the English and, from that, create the quadratic model. Then solve the model for the solutions (that is, the x -intercepts).

Content Continues Below

MathHelp.com

When interpreted — within the context of the exercise — one or both of the solutions to the quadratic equation will provide at least part of the answer they've asked of you.

Advertisement

• A picture has a height that is 4/3 its width. It is to be enlarged to have an area of 192 square inches. What will be the dimensions of the enlargement?

The height is defined in terms of the width, so I'll pick a variable for "width", and then create an expression for the height.

Let " w " stand for the width of the picture. The height h is given as being 4/3 of the width, so:

h = (4/3) w

Then the area, being the product of the width and the height, is given by:

= [(4/3) w ][ w ]

= (4/3) w 2 = 192

I need to solve this "area" equation for the value of the width, and then back-solve to find the value of the height.

(4/3) w 2 = 192 w 2 = 144 w = ± 12

Since I can't have a negative width, I can ignore the " w  = −12 " solution. Then the width must be the other solution, 12 , and the height is then:

h = (4/3)(12) = 16

I can do a quick check of my answer, since this is a "solving" exercise, by plugging my values back into the original exercise. Since 12 × 16 does indeed equal 192 , my answer checks. So my hand-in answer is:

The enlargement will be 12  inches by 16  inches.

• The product of two consecutive negative integers is 1122 . What are the numbers?

Remember that consecutive integers are one unit apart, so my numbers are n and n  + 1 . Multiplying to get the product, I get:

n ( n + 1) = 1122 n 2 + n = 1122 n 2 + n − 1122 = 0 ( n + 34)( n − 33) = 0

The solutions are n  = −34 and n  = 33 . I need a negative value (because the exercise statement specified that the numbers are negative), so I'll ignore the n  = 33 & and take n  = −34 . Then the other number is:

n + 1 = (−34) + 1 = −33

Then my hand-in answer is:

The two numbers are −33 and −34 .

Note that the second value could have been gotten by changing the sign on the extraneous solution. Warning: Many students get in the very bad habit of arbitrarily changing signs to get the answers they need, but this does not always work, and will very likely get them in trouble later on. (And it'll cause trouble right now, if the grader is paying attention.)

Take the extra half a second to find the right answer the right way.

• A garden measuring 12 meters by 16 meters is to have a pedestrian pathway installed all around it, increasing the total area to 285 square meters. What will be the width of the pathway?

The first thing I need to do is draw a picture. Since I don't know how wide the path will be, I'll label the width as " x ".

Looking at my picture, I see that the total width of the finished garden-plus-path area will be:

x + 12 + x = 12 + 2 x

...and the total length will be:

x + 16 + x = 16 + 2 x

Then the new area, being the product of the new width and height, is given by:

(12 + 2 x )(16 + 2 x ) = 285 192 + 56 x + 4 x 2 = 285 4 x 2 + 56 x − 93 = 0

This quadratic is messy enough that I won't bother with trying to use factoring to solve; I'll just go straight to the Quadratic Formula :

Obviously the negative value won't work in this context, so I'll ignore it. Checking the original exercise to verify what I'm being asked to find, I notice that I need to have units on my answer:

The width of the pathway will be 1.5 meters.

• You have to make a square-bottomed, unlidded box with a height of three inches and a volume of approximately 42 cubic inches. You will be taking a piece of cardboard, cutting three-inch squares from each corner, scoring between the corners, and folding up the edges. What should be the dimensions of the cardboard, to the nearest quarter inch?

When dealing with geometric sorts of word problems, it is usually helpful to draw a picture. Since I'll be cutting equal-sized squares out of all of the corners, and since the box will have a square bottom, I know I'll be starting with a square piece of cardboard.

I don't know how big the cardboard will be yet, so I'll label the sides as having length " w ".

Since I know I'll be cutting out three-by-three squares to get sides that are three inches high, I can mark that on my drawing.

The dashed (rather than solid) lines show where I'll be scoring the cardboard and folding up the sides.

Since I'll be losing three inches on either end of the cardboard when I fold up the sides, the final width of the bottom will be the original " w " inches, less three on the one side and another three on the other side. That is, the width of the bottom will be:

w − 3 − 3 = w − 6

The volume will be the product of the width, the length (which is the same as the width), and the depth (which was created by cutting out the corners and folding up the sides).

Then the volume of the box, working from the drawing, gives me the following equation:

( w − 6)( w − 6)(3) = 42 ( w − 6)( w − 6) = 14 ( w − 6) 2 = 14

This is the quadratic I need to solve. I can take the square root of either side, and then add the to the right-hand side:

...or I can multiply out the square and apply the Quadratic Formula :

w 2 − 12 w + 36 = 14

w 2 − 12 w + 22 = 0

Either way, I get two solutions which, when expressed in practical decimal terms, tell me that the width of the original cardboard is either about 2.26 inches or else about 9.74 inches.

How do I know which solution value for the width is right? By checking each value in the original word problem.

If the cardboard is only 2.26 inches wide, then how on earth would I be able to fold up three-inch-deep sides? But if the cardboard is 9.74 inches, then I can fold up three inches of cardboard on either side, and still be left with 3.74 inches in the middle. Checking:

(3.74)(3.74)(3) = 41.9628

This isn't exactly 42 , but, taking round-off error into account, it's close enough that I can trust that I have the correct value. So my hand-in answer, complete with units, is:

The cardboard should measure 9.75  inches on a side.

In this last exercise above, you should notice that each solution method (factoring and the Quadratic Formula) gave the same final answer for the cardboard's width. But the Quadratic Formula took longer and provided me with more opportunities to make mistakes.

Moral? Don't get stuck in the rut of always using the Quadratic Formula.

URL: https://www.purplemath.com/modules/quadprob2.htm

Page 1 Page 2 Page 3

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• Privacy / Cookies
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

In order to access this I need to be confident with:

Quadratic graphs

Quadratic equations

Quadratic equation

Here you will learn about quadratic equations and how to solve quadratic equations using four methods: factoring, using the quadratic formula, completing the square and using a graph.

Students will first learn about quadratic equations as part of geometry in high school.

What is a quadratic equation?

A quadratic equation is a quadratic expression that is equal to something. Quadratic equations are a type of polynomial equation because they consist of algebraic terms, with the highest being second-degree.

A quadratic equation can have zero, one or two solutions. To solve a quadratic equation it must equal 0.

For example,

The standard form of the quadratic equation is:

a{x}^2+bx+c=0

a is the coefficient (number in front) of the x^2 term.

b is the coefficient (number in front) of the x term.

c is the constant term (number on its own).

How to solve quadratic equations

In order to solve a quadratic equation , you must first check that it is in the form

a x^{2}+b x+c=0. If it isn’t, you will need to rearrange the equation.

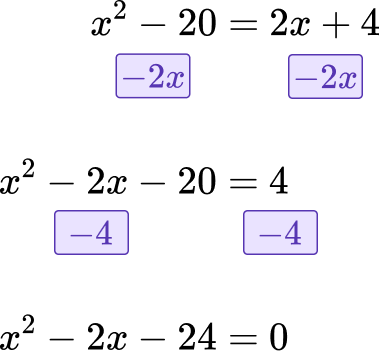
Let’s explore each of the four methods of solving quadratic equations by using the same example: x^{2}-2x-24=0

Step-by-step guide : Solving quadratic equation

a) Quadratic graphs

Solve x^{2}-2x-24=0 by using a quadratic graph.

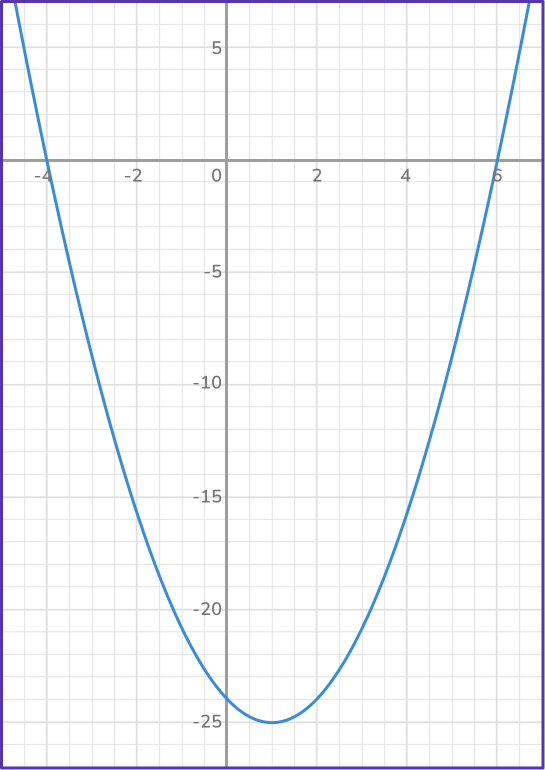
The real roots/solutions are shown where the graph crosses the horizontal x -axis.

x=6 \; and \; x=-4

Step-by-step guide: Solving quadratic equations graphically

b) Completing the square

Solve x^{2}-2x-24=0 by completing the square.

Most quadratic expressions, including this one, are not perfect squares. When you complete the square, you try to fit the expression to the closest possible perfect square, by adding or subtracting to make things work.

First, move c to the right side of the equation.

Then, complete the square and add the square’s c to both sides of the equation.

Since (x-1)^2= x^2-2x +1, add 1 to both sides.

Finally, solve for x.

\sqrt{(x-1)^2}=\sqrt{25} \; *Take the square root of both sides

x-1= \pm \, 5 \; *Solve for –5 and 5

\begin{aligned} x-1&=5 \\ +1 &\;\; +1 \\ x &=6 \quad \text{and} \end{aligned} \begin{aligned} x +1 &=5 \\ -1 & \;\; -1 \\ x &=-4 \end{aligned}

See also: Completing the square

c) Factoring

Solve x^{2}-2x-24=0 by factoring.

Step-by-step guide: Factoring quadratic equations

d) Quadratic formula

You can substitute the values of a, b and c from the general form of the quadratic equation, a x^2+b x+c=0, into the quadratic formula to calculate the solution(s) for the quadratic formula, x.

x=\cfrac{-b\pm\sqrt{b^2-4ac}}{2a}

Solve x^{2}-2x-24=0 using the quadratic formula.

Now, let’s solve for the solutions.

\begin{aligned}& x=\cfrac{-(-2)+\sqrt{(-2)^2-4 \times 1 \times(-24)}}{2 \times 1} \\\\ & x=\cfrac{2+\sqrt{4-(-96)}}{2} \\\\ & x=\cfrac{2+10}{2} \\\\ & x=6\end{aligned} \hspace{0.3cm} \hspace{0.3cm} \begin{aligned}& x=\cfrac{-(-2)-\sqrt{(-2)^2-4 \times 1 \times(-24)}}{2 \times 1} \\\\ & x=\cfrac{2-\sqrt{4-(-96)}}{2} \\\\ & x=\cfrac{2-10}{2} \\\\ & x=-4\end{aligned}

Step-by-step guide: Quadratic formula

[FREE] Math Worksheets

Use these quizzes to check your students’ understanding of math. Contains series of worksheets designed by math experts to identify areas of strength and support!

Common Core State Standards

How does this relate to high school math?

• Algebra – Reasoning with Equations and Inequalities (HSA.REI.B.4a) Use the method of completing the square to transform any quadratic equation in x into an equation of the form (x-p)^2=q that has the same solutions. Derive the quadratic formula from this form.
• Algebra – Reasoning with Equations and Inequalities (HSA.REI.B.4b) Solve quadratic equations in one variable. Solve quadratic equations by inspection (e.g., for x^2=49 ), taking square roots, completing the square, the quadratic formula and factoring, as appropriate to the initial form of the equation. Recognize when the quadratic formula gives complex solutions and write them as a \pm bi for real numbers a and b.

There are a lot of ways to solve quadratic equations. For more specific step-by-step guides, check out the quadratic equation pages linked in the “What is a quadratic equation?” section above or read through the examples below.

Quadratic equation examples

Example 1: solve using a graph.

Solve x^{2}-2 x-24=0 using a graph.

• Graph the quadratic equation.

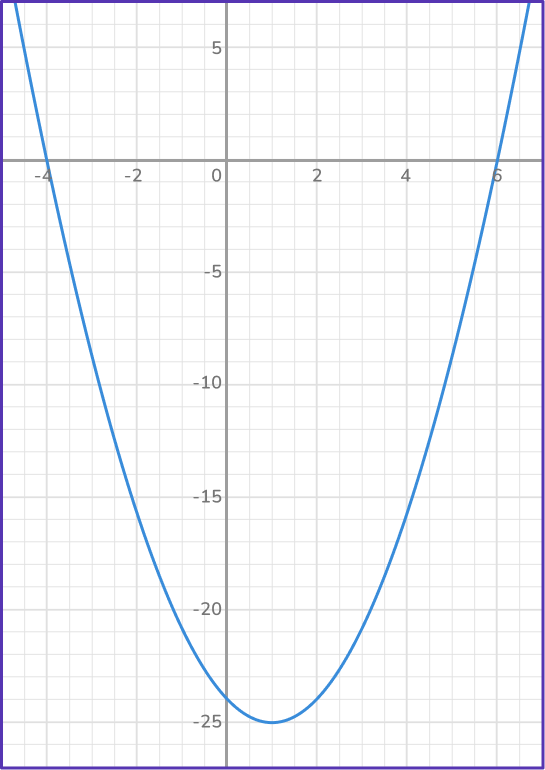
2 Identify where the graph crosses the \textbf{x} -axis (when \bf{\textbf{y}=0} )

You know that to solve a quadratic equation, it must be equal to 0. Since x^2-2 x-24=0 you are looking for the values of x that when substituted into the equation will give us a y value of 0.

On the graph the coordinates for x where y=0 are given where the graph crosses the x axis.

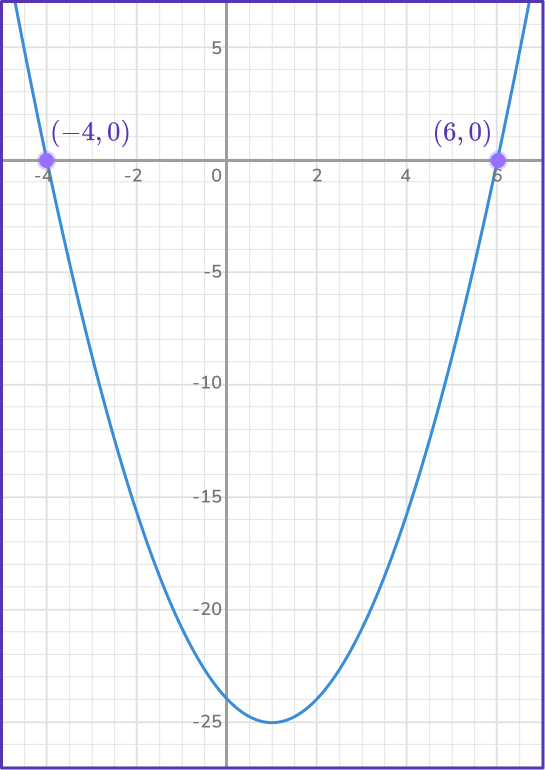
So the solutions or roots of the equation x^{2}-2 x-24=0 are x=6 and x=-4.

You can check that the solution is correct by substituting it into the original equation.

Example 2: solve by completing the square

Solve x^2-4x=12 by completing the square.

Complete the square to rewrite the quadratic equation in the form.

The equation given is already in this form.

Complete the square and add the square’s \textbf{c} to both sides of the equation.

Since (x-2)^2=x^2-4 x+4, add 4 to both sides.

\begin{aligned} x^2-4 x+4&=12+4 \\\\ (x-2)^2&=16\end{aligned}

Rearrange the equation to solve for \textbf{x}.

The square root has a \textbf{+} and \textbf{−} answer. Write down both versions of the calculation to find the two solutions of \textbf{x} .

\begin{aligned}x-2&=4 \\ +2 &\;\; +2 \\ x&=6 \quad \text{and} \end{aligned} \begin{aligned}x-2&=-4 \\ +2 & \;\; +2 \\ x&=-2 \end{aligned}

You can check that our solution is correct by substituting it into the original equation.

Example 3: solve by completing the square

Solve x^2+10x+18.75=0 by completing the square.

Subtract 18.75 from both sides.

\begin{aligned} x^2+10 x+18.75&=0 \\\\ -18.75 &\;\; -18.75 \\\\ x^2+10 x&=-18.75 \end{aligned}

Since (x+5)^2=x^2+10 x+25, add 25 to both sides.

\begin{aligned} x^2+10 x+25&=-18.75+25 \\\\ (x+5)^2&=6.25\end{aligned}

The square root has a \textbf{+} and \textbf{−} answer. Write down both versions of the calculation to find the two solutions of \textbf{x}.

\begin{aligned}x+5&=-2.5 \\ -5 &\;\; -5 \\ x&=-7.5 \quad \text{and} \end{aligned} \begin{aligned}x+5&=2.5 \\ -5 &\;\; -5 \\ x&=-2.5 \end{aligned}

Example 4: solve by factoring

Fully factor the quadratic equation.

You can factor a quadratic into two factors when it is in the form a x^2+b x+c.

When a=1, find the factors of c and see which to have the sum of b.

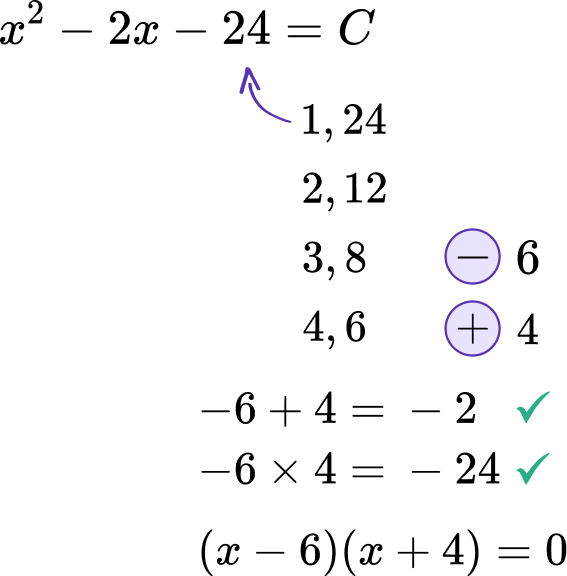
Set each factor equal to \bf{0}.

Solve each equation to find \textbf{x}.

\begin{aligned}x-6&=0 \\ +6 &\;\; +6 \\ x&=6\end{aligned} \quad \quad \begin{aligned}x+4&=0 \\ -4 &\;\; -4 \\ x&=-4 \end{aligned}

Example 5: solve by factoring

Solve x^2+9x-10=0 by factoring.

You can factor a quadratic into two factors when it is in the form a x^2+bx+c.

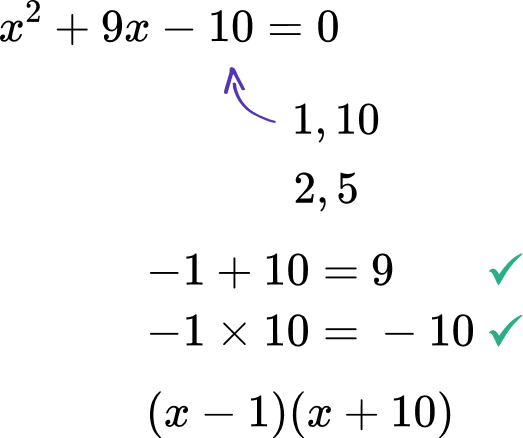
\begin{aligned}x-1&=0 \\ +1 &\;\; +1 \\ x&=1\end{aligned} \quad \quad \begin{aligned}x+10&=0 \\ -10 & \;\; -10 \\ x &=-10 \end{aligned}

Example 6: quadratic equation with complex roots

Solve x^2+2x+2=0.

Identify the value of \textbf{a, b} and \textbf{c} in a quadratic equation.

Substitute these values into the quadratic formula.

Solve the equation with a \textbf{+} , and then with a \textbf{−} .

\begin{aligned}& x=\cfrac{-2+\sqrt{2^2-4(1)(2)}}{2(1)} \\\\ & x=\cfrac{-2+\sqrt{4-8}}{2} \\\\ & x=\cfrac{-2+2 i}{2} \\\\ & x=-1+i\end{aligned} \hspace{1cm} \hspace{1cm} \begin{aligned}& x=\cfrac{-2-\sqrt{2^2-4(1)(2)}}{2(1)} \\\\ & x=\cfrac{-2-\sqrt{4-8}}{2} \\\\ & x=\cfrac{-2-2 i}{2} \\\\ & x=-1-i\end{aligned}

Note, since \sqrt{4-8}=\sqrt{-4}, you use a complex number to represent the square root.

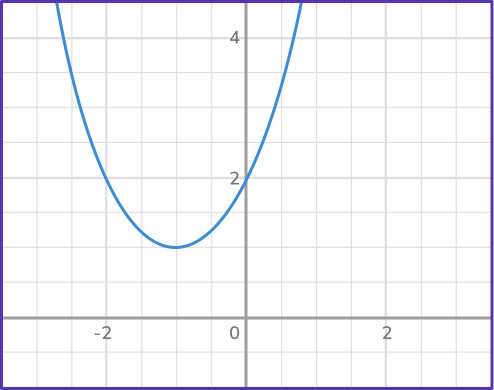
The roots are imaginary numbers, because this parabola does not cross the x -axis.

Teaching tips for quadratic equation

• Allow students use a graphing calculator to input different values for a, b and c in a quadratic equation and explore how changing the values changes the parabola.
• After graphing, many curriculums start with the square method, as it is usually the easiest for students to understand when beginning to solve quadratic equations. However, always do what is best for your students.
• Allow students who are struggling to use a calculator for all computations, since these are not the focus of this skill.
• There are many free quadratic equation solvers on the internet. Students can use these to check their work when solving with any method.

Easy mistakes to make

• Forgetting to calculate both solutions for the quadratic formula The quadratic formula includes an operation with both a positive sign and negative sign. This is because it involves the calculation of the square root of the discriminant. Don’t forget to calculate both solutions.
• Thinking that quadratic equations only look like \bf{\textbf{ax}^2+\textbf{bx}+\textbf{c}=0} A quadratic equation is any equation where the highest term is x^2 (or any second-order polynomial). Quadratic equations do not have to come in the form a x^2+b x+c=0, but since they are algebraic equations they can always be simplified to this form. For example, Simplify 3 x^2-3 x=2 x^2+14 to the form ax^2+bx+c=0. 3 x^2-3 x=2 x^2+14 \quad -2 x^2 \quad -2 x^2 \;\; x^2-3 x=14 \quad -14 \quad -14 x^2-3 x-14=0
• Forgetting to move all parts to the left-hand side before using the quadratic formula The values for a, b and c in the quadratic formula will only work for a quadratic expression set equal to 0. For example, Before using the quadratic equation to solve 4 x^2-9 x=12, you need to subtract 12 from both sides so that the equation is in the form 4 x^2-9 x-12=0.

Practice quadratic equation questions

1. Solve 2 x^2+x-3 by using its graph below.

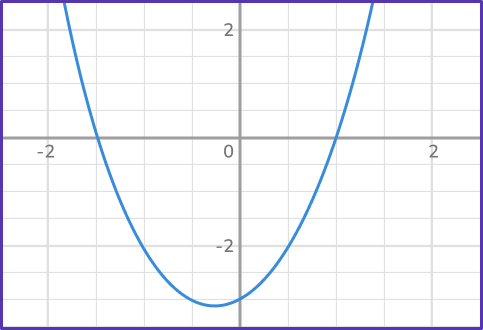
The roots of a quadratic equation are where the parabola passes through the x -axis. In this graph, it passes at (–1.5,0) and (1,0).

The solutions are x = –1.5 and x = 1.

2. Complete the square to solve the given quadratic equation:

Complete the square and add the square’s c to both sides of the equation.

Since (x-4)^2=x^2-8 x+16, add 16 to both sides.

Rearrange the equation to solve for x.

\begin{aligned}x-4&=5 \\ +4 & \;\; +4 \end{aligned} \quad \quad \begin{aligned}x-4&=-5 \\ +4 & \;\; +4 \end{aligned}

\quad \;\; x=9 \quad and \;\, \quad x=-1

3. Complete the square to solve the given quadratic equation:

First, solve so that c is on the right-hand side of the equation.

Since (x+10)^2=x^2+20 x+100, add 100 to both sides.

\quad \quad x+10= \pm \, 9.95 \quad *rounded to the nearest hundredth

\begin{aligned}x+10 &= 9.95 \\ -10 & \;\; -10 \\ x&=-0.05 \quad \; \text{and} \end{aligned} \begin{aligned}x+10 &=-9.95 \\ -10 & \;\; -10 \\ x&=19.95\end{aligned}

4. Solve by factoring 2 x^2+8 x-10=0.

Find the factors of ac, which is 2 \times-10=-20.

The sum of ac should be b, or 8.

-2 +10=8, so use these to write an equivalent equation.

Then group the terms and factor out the GCF.

\begin{aligned}2 x-2&=0 \\ +2 & \;\; +2 \\ 2x&=2 \\ x &=1 \quad \text{and} \end{aligned} \begin{aligned}x+5&=0 \\ -5 & \;\; -5 \\ & \\ x&=-5\end{aligned}

Note, that the factoring could also result in (2 x+10)(x-1), which leads to the same roots.

5. Solve 3{x}^2+5x-2=0 using the quadratic formula.

Identify a, b and c.

Solve the equation with a +, and then with a -.

\begin{aligned}& x=\cfrac{-5+\sqrt{5^2-4(3)(-2)}}{2(3)} \\\\ & x=\cfrac{-5+\sqrt{25-(-24)}}{6} \\\\ & x=\cfrac{-5+7}{6} \\\\ & x=\cfrac{1}{3}\end{aligned} \hspace{1cm} \hspace{1cm} \begin{aligned}& x=\cfrac{-5-\sqrt{5^2-4(3)(-2)}}{2(3)} \\\\ & x=\cfrac{-5-\sqrt{25-(-24)}}{6} \\\\ & x=\cfrac{-5-7}{6} \\\\ & x=-2\end{aligned}

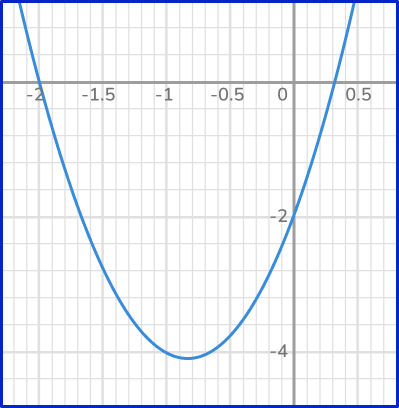
6. Solve -4 x^2+2 x-6=0 using the quadratic formula.

\begin{aligned}& x=\cfrac{2+\sqrt{2^2-4(-4)(-6)}}{2(-4)} \\\\ & x=\cfrac{2+\sqrt{4-96}}{-8} \\\\ & x=\cfrac{2+\sqrt{92} i}{-8} \\\\ & x=-\cfrac{1}{4}-1.199 i\end{aligned} \hspace{1cm} \hspace{1cm} \begin{aligned}& x=\cfrac{2-\sqrt{2^2-4(-4)(-6)}}{2(-4)} \\\\ & x=\cfrac{2-\sqrt{4-96}}{-8} \\\\ & x=\cfrac{2-\sqrt{92 i}}{-8} \\\\ & x=-\cfrac{1}{4}+1.199 i\end{aligned}

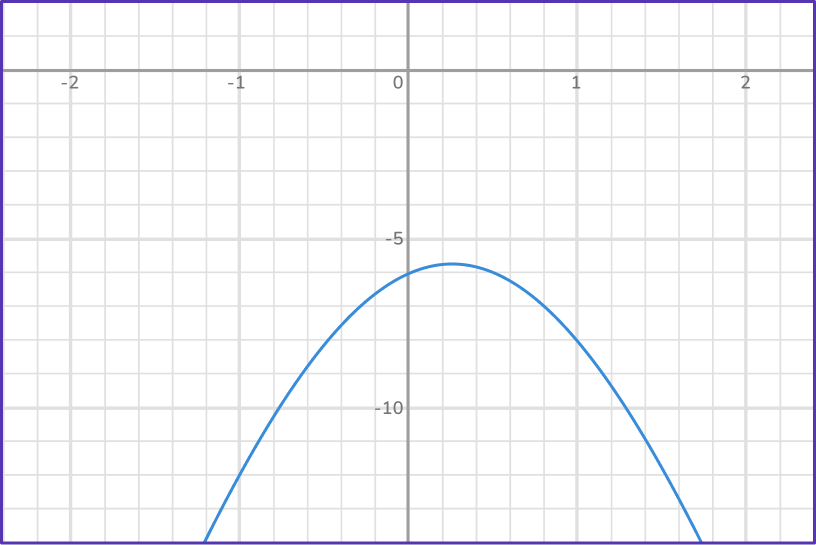
You can see that there are no values of x that give a y value of 0.

The graph does not cross the x -axis. The use of the quadratic formula will result in roots that are not real.

Quadratic equation FAQs

Calculate the discriminant \left(b^2-4 a c\right). If the discriminant is equal to 0, it has 1 distinct root. This is because the parabola’s vertex lies on the x -axis, so it only crosses once. If the discriminant is greater than 0, it has 2 distinct roots that are real solutions. If the discriminant is less than 0, it has 2 distinct roots that are complex solutions.

The values for b and c can be any real number, including rational numbers, fractions, decimals, integers or whole numbers.

The next lessons are

• Angles in parallel lines

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

Free Mathematics Tutorials

Quadratic functions problems with solutions.

quadratic functions problems with detailed solutions are presented along with graphical interpretations of the solutions.

Review Vertex and Discriminant of Quadratic Functions

f(x) = a x 2 + b x + c

If a > 0 , the vertex is a minimum point and the minimum value of the quadratic function f is equal to k. This minimum value occurs at x = h. If a < 0 , the vertex is a maximum point and the maximum value of the quadratic function f is equal to k. This maximum value occurs at x = h. The quadratic function f(x) = a x 2 + b x + c can be written in vertex form as follows:

f(x) = a (x - h) 2 + k

Problems with Solutions

Problem 1 The profit (in thousands of dollars) of a company is given by.

P(x) = 5000 + 1000 x - 5 x 2

• Function P that gives the profit is a quadratic function with the leading coefficient a = - 5. This function (profit) has a maximum value at x = h = - b / (2a) x = h = -1000 / (2(-5)) = 100
• The maximum profit Pmax, when x = 100 thousands is spent on advertising, is given by the maximum value of function P k = c - b 2 / (4 a) b)
• The maximum profit Pmax, when x = 100 thousands is spent on advertising, is also given by P(h = 100) P(100) = 5000 + 1000 (100) - 5 (100) 2 = 55000.
• When the company spends 100 thousands dollars on advertising, the profit is maximum and equals 55000 dollars.

Problem 2 An object is thrown vertically upward with an initial velocity of V o feet/sec. Its distance S(t), in feet, above ground is given by

• S(t) is a quadratic function and the maximum value of S(t)is given by k = c - b 2 /(4 a) = 0 - (v o ) 2 / (4(-16))
• This maximum value of S(t) has to be 300 feet in order for the object to reach a maximum distance above ground of 300 feet. - (v o ) 2 / (4(-16)) = 300
• we now solve - (v o ) 2 / (4(-16)) = 300 for v o v o = 64*300 = 80 √3 feet/sec.

Problem 3 Find the equation of the quadratic function f whose graph passes through the point (2 , -8) and has x intercepts at (1 , 0) and (-2 , 0). Solution to Problem 3

• Since the graph has x intercepts at (1 , 0) and (-2 , 0), the function has zeros at x = 1 and x = - 2 and may be written as follows. f(x) = a (x - 1)(x + 2)
• The graph of f passes through the point (2 , -8), it follows that f(2) = - 8
• which leads to - 8 = a (2 - 1)(2 + 2)
• expand the right side of the above equation and group like terms -8 = 4 a
• Solve the above equation for a to obtain a = - 2
• The equation of f is given by f(x) = - 2 (x - 1)(x + 2)
• Check answer f(1) = 0 f(-2) = 0 f(2) = - 2 (2 - 1)(2 + 2) = -8

Problem 4 Find values of the parameter m so that the graph of the quadratic function f given by

• To find the points of intersection, you need to solve the system of equations y = x 2 + x + 1 y = m x
• Substitute m x for y in the first equation to obtain mx = x 2 + x + 1
• Write the above quadratic equation in standard form. x 2 + x (1 - m) + 1 = 0
• Find the discriminant D of the above equation. D = (1 - m) 2 - 4(1)(1) D = (1 - m) 2 - 4 a)
• For the graph of f and that of the line to have 2 points of intersection, D must be positive, which leads to (1 - m) 2 - 4 > 0
• Solve the above inequality to obtain solution set for m in the intervals (- ∞ , -1) U (3 , + ∞) b)
• For the graph of f and that of the line to have 1 point of intersection, D must be zero, which leads to (1 - m) 2 - 4 = 0
• Solve the above equation to obtain 2 solutions for m. m = -1 m = 3 c)
• For the graph of f and that of the line to have no points of intersection, D must be negative, which leads to (1 - m) 2 - 4 < 0

Problem 5 The quadratic function C(x) = a x 2 + b x + c represents the cost, in thousands of Dollars, of producing x items. C(x) has a minimum value of 120 thousands for x = 2000 and the fixed cost is equal to 200 thousands. Find the coefficients a,b and c. Solution to Problem 5

• Function C is a quadratic function. Its minimum point, which is given as (2000,120) is the vertex of the graph of C. Hence we can write C(x) in vertex form as follows C(x) = a (x - 2000) 2 + 120
• The fixed cost is the value of C(x) when x = 0. Hence C(0) = a (0 - 2000) 2 + 120 = 200
• Solve for a a = 80 / 2000 2 = 0.00002
• We expand C(x) and identify the coefficients a, b and c. C(x) = 0.00002 (x - 2000) 2 + 120 = 0.00002 x 2 - 0.08 x + 200 a = 0.00002 , b = -0.08 and c = 200.

Problem 6 Find the equation of the tangent line to the the graph of f(x) = - x 2 + x - 2 at x = 1. Solution to Problem 6

• There are at least two methods to solve the above question. Method 1
• Let the equation of the tangent line be of the form y = m x + b
• and we therefore need to find m and b. The tangent line passes through the point (1 , f(1)) = (1 , -2)
• Hence the equation in m and b - 2 = m (1) + b or m + b = -2
• To find the point of tangency of the line and the graph of the quadratic function, we need to solve the system y = m x + b and y = - x 2 + x - 2
• Substitute y by m x + b in the second equation of the system to obtain m x + b = - x 2 + x - 2
• Write the above equation in standard form - x 2 + x (1 - m) - 2 - b = 0
• For the line to be tangent to the graph of the quadratic function, the discriminant D of the above equation must be equal to zero. Hence D = b 2 - 4 a c = (1 - m) 2 - 4 (-1) (- 2 - b) = 0
• which gives (1 - (- 2 - b) ) 2 + 4 (- 2 - b) = 0
• Expand, simplify and write the above equation in standard form b 2 2 b + 1 = 0 (b + 1) 2 = 0
• Solve for b b = - 1
• Find m m = - 2 - b = -1

Questions with Solutions

Find the equation of the quadratic function f whose graph has x intercepts at (-1 , 0) and (3 , 0) and a y intercept at (0 , -4).

Question 2 Find values of the parameter c so that the graphs of the quadratic function f given by f(x) = x 2 + x + c and the graph of the line whose equation is given by y = 2 x have: a) 2 points of intersection, b) 1 point of intersection, c) no points of intersection.

Solutions to the Above Questions

Solution to Question 1

• The x intercepts of the graph of f are the zero of f(x). Hence f(x) is of the form f(x) = a (x + 1)(x - 3)
• We now need to find coefficient a using the y intercept f(0) = a(0 + 1)(0 - 3) = - 4
• Solve for a a = 4 / 3
• Hence f(x) = (4 / 3) (x + 1)(x - 3)

Solution to Question 2

• To find the coordinates of the point of intersections of the graphs of f(x) = x 2 + x + c and y = 2 x, we need to solve the system y = x 2 + x + c and y = 2 x
• which by substitution , gives the equation x 2 + x + c = 2x
• Rewrite the above equation in standard form x 2 - x + c = 0
• Find the discriminant D D = 1 - 4 c
• Conclusion If D is positive or c < 1 / 4 , the two graphs intersect at two points. If D is equal to 0 or c = 1 / 4 , the two graphs intersect (touch) at 1 point. If D is negative or c > 1 / 4 , the two graphs have no point of intersection.

More References and Links to Quadratic Functions

• Math Questions With Answers (13): Quadratic Functions.
• Vertex and Intercepts Parabola Problems.
• Find Vertex and Intercepts of Quadratic Functions - Calculator: An applet to solve calculate the vertex and x and y intercepts of the graph of a quadratic function.
• Quadratic functions (general form).
• Quadratic functions (standard form).
• Graphing quadratic functions.
• Solver to Analyze and Graph a Quadratic Function

Popular Pages

Resource links, share with us.

  ©2024 analyzemath.com    

• Privacy Policy

• Math Article

Quadratic Equation Questions

Quadratic equation questions are provided here for Class 10 students. A quadratic equation is a second-degree polynomial which is represented as ax 2 + bx + c = 0, where a is not equal to 0. Here, a, b and c are constants, also called coefficients and x is an unknown variable. Also, learn Quadratic Formula here.

Solving the problems based on quadratics will help students to understand the concept very well and also to score good marks in this section. All the questions are solved here step by step with a detailed explanation. In this article, we will give the definition and important formula for solving problems based on quadratic equations. The questions given here is in reference to the CBSE syllabus and NCERT curriculum. 

Definition of Quadratic Equation

Usually, the quadratic equation is represented in the form of ax 2 +bx+c=0, where x is the variable and a,b,c are the real numbers & a ≠ 0. Here, a and b are the coefficients of x 2 and x, respectively. So, basically, a quadratic equation is a polynomial whose highest degree is 2. Let us see some examples:

• 3x 2 +x+1, where a=3, b=1, c=1
• 9x 2 -11x+5, where a=9, b=-11, c=5

Roots of Quadratic Equations:

If we solve any quadratic equation, then the value we obtain are called the roots of the equation. Since the degree of the quadratic equation is two, therefore we get here two solutions and hence two roots.

There are different methods to find the roots of quadratic equation, such as:

• Factorisation
• Completing the square
• Using quadratic formula

Learn: Factorization of Quadratic equations

Quadratic Equation Formula:

The quadratic formula to find the roots of the quadratic equation is given by:

\(\begin{array}{l}x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}\end{array} \)

Where b 2 -4ac is called the discriminant of the equation.

Based on the discriminant value, there are three possible conditions, which defines the nature of roots as follows:

• two distinct real roots, if b 2 – 4ac > 0
• two equal real roots, if b 2 – 4ac = 0
• no real roots, if b 2 – 4ac < 0

Also, learn quadratic equations for class 10 here.

Quadratic Equations Problems and Solutions

1. Rahul and Rohan have 45 marbles together. After losing 5 marbles each, the product of the number of marbles they both have now is 124. How to find out how many marbles they had to start with.

Solution: Say, the number of marbles Rahul had be x.

Then the number of marbles Rohan had = 45 – x.

The number of marbles left with Rahul after losing 5 marbles = x – 5

The number of marbles left with Rohan after losing 5 marbles = 45 – x – 5 = 40 – x

The product of number of marbles = 124

(x – 5) (40 – x) = 124

40x – x 2 – 200 + 5x = 124

– x 2 + 45x – 200 = 124

x 2 – 45x + 324 = 0

This represents the quadratic equation. Hence by solving the given equation for x, we get;

x = 36 and x = 9

So, the number of marbles Rahul had is 36 and Rohan had is 9 or vice versa.

2. Check if x(x + 1) + 8 = (x + 2) (x – 2) is in the form of quadratic equation.

Solution: Given,

x(x + 1) + 8 = (x + 2) (x – 2)

Cancel x 2 both the sides.

Since, this expression is not in the form of ax 2 +bx+c, hence it is not a quadratic equation.

3. Find the roots of the equation 2x 2 – 5x + 3 = 0 using factorisation.

2x 2 – 5x + 3 = 0

2x 2 – 2x-3x+3 = 0

2x(x-1)-3(x-1) = 0

(2x-3) (x-1) = 0

2x-3 = 0; x = 3/2

(x-1) = 0; x=1

Therefore, 3/2 and 1 are the roots of the given equation.

4. Solve the quadratic equation 2x 2 + x – 300 = 0 using factorisation.

Solution: 2x 2 + x – 300 = 0

2x 2 – 24x + 25x – 300 = 0

2x (x – 12) + 25 (x – 12) = 0

(x – 12)(2x + 25) = 0

x-12=0; x=12

(2x+25) = 0; x=-25/2 = -12.5

Therefore, 12 and -12.5 are two roots of the given equation.

Also, read   Factorisation .

5. Solve the equation x 2 +4x-5=0.

x 2 + 4x – 5 = 0

x 2 -1x+5x-5 = 0

x(x-1)+5(x-1) =0

(x-1)(x+5) =0

Hence, (x-1) =0, and (x+5) =0

similarly, x+5 = 0

x=-5 & x=1

6. Solve the quadratic equation 2x 2 + x – 528 = 0, using quadratic formula.

Solution: If we compare it with standard equation, ax 2 +bx+c = 0

a=2, b=1 and c=-528

Hence, by using the quadratic formula:

Now putting the values of a,b and c.

x=64/4 or x=-66/4

x=16 or x=-33/2

7. Find the roots of x 2 + 4x + 5 = 0, if any exist, using quadratic formula.

Solution: To check whether there are real roots available for the quadratic equation, we need the find the discriminant value.

D = b 2 -4ac = 4 2 – 4(1)(5) = 16-20 = -4

Since the square root of -4 will not give a real number. Hence there is no real roots for the given equation.

8. Find the discriminant of the equation: 3x 2 -2x+⅓ = 0.

Solution: Here, a = 3, b=-2 and c=⅓

Hence, discriminant, D = b 2 – 4ac

D = (-2) 2 -4(3)(⅓)

Video Lesson

Quadratic equation worksheet.

Practice Questions

Solve these quadratic equations and find the roots. 

• x 2 -5x-14=0         [Answer: x=-2 & x=7]
• X 2  = 11x -28       [Answer: x=4 & x = 7]
• 6x 2 – x = 5            [Answer: x=-⅚ & x = 1]
• 12x 2 = 25x          [Answer: x=0 & x=25/12]

Frequently Asked Questions on Quadratic Equations

What is a quadratic equation, what are the examples of quadratic equations, what is the formula for quadratics, what are the methods to solve the quadratic equation, what are the roots of the quadratic equation, what are the zeroes of the quadratic equation, leave a comment cancel reply.

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Thank you so much for providing this

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Quadratic Formula Practice Questions

Click here for questions, click here for answers.

GCSE Revision Cards

5-a-day Workbooks

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• ax^2+bx+c=0
• x^2+2x+1=3x-10
• 2x^2+4x-6=0
• How do you calculate a quadratic equation?
• To solve a quadratic equation, use the quadratic formula: x = (-b ± √(b^2 - 4ac)) / (2a).
• What is the quadratic formula?
• The quadratic formula gives solutions to the quadratic equation ax^2+bx+c=0 and is written in the form of x = (-b ± √(b^2 - 4ac)) / (2a)
• Does any quadratic equation have two solutions?
• There can be 0, 1 or 2 solutions to a quadratic equation. If the discriminant is positive there are two solutions, if negative there is no solution, if equlas 0 there is 1 solution.
• What is quadratic equation in math?
• In math, a quadratic equation is a second-order polynomial equation in a single variable. It is written in the form: ax^2 + bx + c = 0 where x is the variable, and a, b, and c are constants, a ≠ 0.
• How do you know if a quadratic equation has two solutions?
• A quadratic equation has two solutions if the discriminant b^2 - 4ac is positive.

quadratic-equation-calculator

• High School Math Solutions – Quadratic Equations Calculator, Part 2 Solving quadratics by factorizing (link to previous post) usually works just fine. But what if the quadratic equation...

Please add a message.

Message received. Thanks for the feedback.