hypothesis of value

Blog » Value Hypothesis & Growth Hypothesis: lean startup validation

Value Hypothesis & Growth Hypothesis: lean startup validation

Posted on September 16, 2021 |

You’ve come up with a fantastic idea for a startup and you need to discuss the hypothesis and its value? But you’re not sure if it’s a viable one or not. What do you do next? It’s essential to get your ideas right before you start developing them. 95% of new products fail in their first year of launch. Or to put it another way, only one in twenty product ideas succeed. In this article, we’ll be taking a look at why it’s so important to validate your startup idea before you start spending a lot of time and money developing it. And that’s where the Lean Startup Validation process gets into, alongside the growth hypothesis and value hypothesis. We’ll also be looking at the questions that you need to ask.

Table of contents

The lean startup validation methodology, the benefits of validating your startup idea, the value hypothesis, the growth hypothesis, recommendations and questions for creating and running a good hypothesis, in conclusion – take the time to validate your product.

What does it mean to validate a lean startup?

Validating your lean startup idea may sound like a complicated process, but it’s a lot simpler than you may think. It may be the case that you were already planning on carrying out some of the work.

Essentially, validating your startup when you check your idea to see if it solves a problem that your prospective customers have. You can do this by creating hypotheses and then carrying out research to see if these hypotheses are true or false. 

The best startups have always been about finding a gap in the market and offering a product or service that solves the problem. For example, take Airbnb . Before Airbnb launched, people only had the option of staying in hotels. Airbnb opened up the hospitality industry, offering cheaper accommodation to people who could not afford to stay inexpensive hotels. 

“Don’t be in a rush to get big. Be in a rush to have a great product” – Eric Ries

Validation is a crucial part of the lean startup methodology, which was devised by entrepreneur Eric Ries. The lean startup methodology is all about optimizing the amount of time that is needed to ensure a product or service is viable. 

Lean Startup Validation is a critical part of the lean startup process as it helps make sure that an idea will be successful before time is spent developing the final product.

As an example of a failed idea where more validation could have helped, take Google Glass . It sounded like a good idea on paper, but the technology failed spectacularly. Customer research would have shown that $1,500 was too much money, that people were worried about health and safety, and most importantly… there was no apparent benefit to the product.

Find out more about lean startup methodology on our blog

How to create a mobile app using lean startup methodology

The key benefit of validating your lean startup idea is to make sure that the idea you have is a viable one before you start using resources to build and promote it. 

There are other less obvious benefits too:

• It can help you fine-tune your idea. So, it may be the case that you wanted your idea to go in a particular direction, but user research shows that pivoting may be the best thing to do
• It can help you get funding. Investors may be more likely to invest in your startup idea if you have evidence that your idea is a viable one

The value hypothesis and the growth hypothesis – are two ways to validate your idea

“To grow a successful business, validate your idea with customers” – Chad Boyda

In Eric Rie’s book ‘ The Lean Startup’ , he identifies two different types of hypotheses that entrepreneurs can use to validate their startup idea – the growth hypothesis and the value hypothesis. 

Let’s look at the two different ideas, how they compare, and how you can use them to see if your startup idea could work.

The value hypothesis tests whether your product or service provides customers with enough value and most importantly, whether they are prepared to pay for this value.

For example, let’s say that you want to develop a mobile app to help dog owners find people to help walk their dogs while they are at work. Before you start spending serious time and money developing the app, you’ll want to see if it is something of interest to your target audience. 

Your value hypothesis could say, “we believe that 60% of dog owners aged between 30 and 40 would be willing to pay upwards of €10 a month for this service.”

You then find dog owners in this age range and ask them the question. You’re pleased to see that 75% say that they would be willing to pay this amount! Your hypothesis has worked! This means that you should focus your app and your advertising on this target audience. 

If the data comes back and says your prospective target audience isn’t willing to pay, then it means you have to rethink and reframe your app before running another hypothesis. For example, you may want to focus on another demographic, or look at reducing the price of the subscription.

Shoe retailer Zappos used a value hypothesis when starting out. Founder Nick Swinmurn went to local shoe stores, taking photos of the shoes and posting them on the Zappos website. Then, if customers bought the shoes, he’d buy them from the store and send them out to them. This allowed him to see if there was interest in his website, without having to spend lots of money on stock.

The growth hypothesis tests how your customers will find your product or service and shows how your potential product could grow over the years.

Let’s go back to the dog-walking app we talked about earlier. You think that 80% of app downloads will come from word-of-mouth recommendations.

You create a minimal viable product ( MVP for short ) – this is a basic version of your app that may not contain all of the features just yet. So, you then upload it to the app stores and wait for people to start downloading it. When you have a baseline of customers, you send them an email asking them how they heard of your app.

When the feedback comes back, it shows that only 30% of downloads have come from word-of-mouth recommendations. This means that your growth hypothesis has not been successful in this scenario. 

Does this mean that your idea is a bad one? Not necessarily. It just means that you may have to look at other ways of promoting your app. If you are relying on word-of-mouth recommendations to advertise it, then it could potentially fail.

Dropbox used growth hypotheses to its advantage when creating its software. The file-storage company constantly tweaked its website, running A/B tests to see which features and changes were most popular with customers, using them in the final product.

Like any good science experiment, there are things that you need to bear in mind when running your hypotheses. Here are our recommendations:

• You may be wondering which type of hypothesis you should carry out first – a growth hypothesis or a value hypothesis. Eric Ries recommends carrying out a value hypothesis first, as it makes sense to see if there is interest before seeing how many people are interested. However, the precise order may depend on the type of product or service you want to sell;
• You will probably need to run multiple hypotheses to validate your product or service. If you do this, be sure to only test one hypothesis at a time. If you end up testing multiple ones in one go, you may not be sure which hypothesis has had which result;
• Test your most critical assumption first – this is one that you are most worried about, and could affect your idea the most. It may be that solving this issue makes your product or service a viable one;
• Specific – is your hypothesis simple? If it’s jumbled or confusing, you’re not going to get the best results from it. If you’re struggling to put together a clear hypothesis, it’s probably a sign to go back to the drawing board.
• Measurable – can your hypothesis be measured? You’ll want to get tangible results so you can check if the changes you have made have worked.
• Achievable – is your hypothesis attainable? If not, you may want to break it down into smaller goals.
• Relevant – will your hypothesis prove the validity of your product or service? 
• Timely – can your hypothesis be measured in a set amount of time? You don’t want a goal that will take years to monitor and measure!
• Be as critical as possible. If you have created an idea, it is only natural that you want it to succeed. However, being objective rather than subjective will help your startup most in the long term;
• When you are carrying out customer research, use as vast a pool of people as time and money will allow. This will result in more accurate data. The great news is that you can use social media and other networking sites to reach out to potential customers and ask them their opinions;
• When carrying out customer research, be sure to ask the questions that matter. Bear in mind that liking your product or service isn’t the same as buying it. If a customer is enthusiastic about your idea, be sure to ask follow-on questions about why they like it, or if they would be willing to spend money on it. Otherwise, your data may end up being useless;
• While it is essential to have as many relevant hypotheses as possible, be careful not to have too many.  While it may sound like a good idea to try out lots of different ideas, it can actually be counter-productive. As Eric Ries said:

“Don’t bog new teams down with too much information about falsifiable hypotheses. Because if we load our teams up with too much theory, they can easily get stuck in analysis paralysis. I’ve worked with teams that have come up with hundreds of leap-of-faith assumptions. They listed so many assumptions that were so detailed and complicated that they couldn’t decide what to do next. They were paralyzed by the just sheer quantity of the list.”

“We must learn what customers really want, not what they say they want or what we think they should want.” – Eric Ries

According to CB Insights , the number one reason why startups fail is that there is no demand for the product. Many entrepreneurs have gone ahead and launched a product that they think people want, only to find that there is no market at all.

Lean Startup Validation is essential in helping your business idea to succeed. While it may seem like extra work, the additional work you do in the beginning will be of a critical advantage later down the line.

Still not 100% convinced? Take HubSpot . Before HubSpot launched its sales and marketing services, it started off as a blog. Co-founders Dharmesh Shah and Brian Halligan used this blog to validate their ideas and see what their visitors wanted. This helped them confirm that their concept was on the right lines and meant they could launch a product that people actually wanted to use.

Validating a startup idea before development is crucial because it ensures that the idea is viable and addresses a real problem that customers have. With a high failure rate of new products, validation helps avoid wasting time and resources on ideas that might not succeed.

The value hypothesis tests whether customers find enough value in a product or service to pay for it. The growth hypothesis examines how customers will discover and adopt the product over time. Both hypotheses are essential for validating the viability of a startup idea.

Eric Ries recommends starting with a value hypothesis before a growth hypothesis. Validating whether the idea provides value is crucial before considering how to promote and grow it.

When creating and running a hypothesis, consider the following: 1. Focus on testing one hypothesis at a time. 2. Test your most critical assumptions first. 3. Ensure your hypothesis follows SMART goals (Specific, Measurable, Achievable, Relevant, Timely). 4. Use a wide pool of potential customers for accurate data. 5. Ask relevant and probing questions during customer research. 6. Avoid overwhelming your team with excessive hypotheses.

Validating your product idea before development helps you avoid the top reason for startup failure—lack of demand for the product. By confirming that there is a market need and interest in your idea, you increase the chances of building a successful product.

Lean Startup Validation helps entrepreneurs avoid the mistake of launching a product that doesn’t address a genuine need. By gathering evidence and feedback early, you can make informed decisions about pivoting or refining your idea before investing significant time and resources.

Certainly. Suppose you’re developing a mobile app for dog owners to find dog-walking services. Your value hypothesis could be: “We believe that 60% of dog owners aged between 30 and 40 would be willing to pay upwards of €10 a month for this service.” You then validate this hypothesis by surveying dog owners in that age range and analyzing their responses.

The growth hypothesis examines how customers will discover and adopt your product. If, for example, you expect 80% of app downloads to come from word-of-mouth recommendations, but feedback shows only 30% are from this source, you may need to reevaluate your promotion strategy.

Yes, Lean Startup Validation can be applied to startups across various industries. Whether you’re offering a product or service, the process of testing hypotheses and gathering evidence applies universally to ensure the viability of your idea.

To gather accurate data, focus on reaching a diverse pool of potential customers through various channels, including social media and networking sites. Ask relevant questions about their preferences, willingness to pay, and potential pain points related to your idea

Being critical and objective during validation helps you avoid confirmation bias and wishful thinking. Objectivity allows you to assess whether your idea truly addresses a problem and resonates with customers, ensuring that your startup’s foundation is built on solid evidence.

Launching Startups that get Success Stories

Contact us:

Quick links

© 2016 - 2024 URLAUNCHED LTD. All Rights Reserved

12 min read

Value Hypothesis 101: A Product Manager's Guide

Talk to sales.

Humans make assumptions every day—it’s our brain’s way of making sense of the world around us, but assumptions are only valuable if they're verifiable . That’s where a value hypothesis comes in as your starting point.

A good hypothesis goes a step beyond an assumption. It’s a verifiable and validated guess based on the value your product brings to your real-life customers. When you verify your hypothesis, you confirm that the product has real-world value, thus you have a higher chance of product success. 

What Is a Verifiable Value Hypothesis?

A value hypothesis is an educated guess about the value proposition of your product. When you verify your hypothesis , you're using evidence to prove that your assumption is correct. A hypothesis is verifiable if it does not prove false through experimentation or is shown to have rational justification through data, experiments, observation, or tests. 

The most significant benefit of verifying a hypothesis is that it helps you avoid product failure and helps you build your product to your customers’ (and potential customers’) needs. 

Verifying your assumptions is all about collecting data. Without data obtained through experiments, observations, or tests, your hypothesis is unverifiable, and you can’t be sure there will be a market need for your product. 

A Verifiable Value Hypothesis Minimizes Risk and Saves Money

When you verify your hypothesis, you’re less likely to release a product that doesn’t meet customer expectations—a waste of your company’s resources. Harvard Business School explains that verifying a business hypothesis “...allows an organization to verify its analysis is correct before committing resources to implement a broader strategy.” 

If you verify your hypothesis upfront, you’ll lower risk and have time to work out product issues. 

UserVoice Validation makes product validation accessible to everyone. Consider using its research feature to speed up your hypothesis verification process. 

Value Hypotheses vs. Growth Hypotheses 

Your value hypothesis focuses on the value of your product to customers. This type of hypothesis can apply to a product or company and is a building block of product-market fit . 

A growth hypothesis is a guess at how your business idea may develop in the long term based on how potential customers may find your product. It’s meant for estimating business model growth rather than individual products. 

Because your value hypothesis is really the foundation for your growth hypothesis, you should focus on value hypothesis tests first and complete growth hypothesis tests to estimate business growth as a whole once you have a viable product.

4 Tips to Create and Test a Verifiable Value Hypothesis

A verifiable hypothesis needs to be based on a logical structure, customer feedback data , and objective safeguards like creating a minimum viable product. Validating your value significantly reduces risk . You can prevent wasting money, time, and resources by verifying your hypothesis in early-stage development. 

A good value hypothesis utilizes a framework (like the template below), data, and checks/balances to avoid bias. 

1. Use a Template to Structure Your Value Hypothesis 

By using a template structure, you can create an educated guess that includes the most important elements of a hypothesis—the who, what, where, when, and why. If you don’t structure your hypothesis correctly, you may only end up with a flimsy or leap-of-faith assumption that you can’t verify. 

A true hypothesis uses a few guesses about your product and organizes them so that you can verify or falsify your assumptions. Using a template to structure your hypothesis can ensure that you’re not missing the specifics.

You can’t just throw a hypothesis together and think it will answer the question of whether your product is valuable or not. If you do, you could end up with faulty data informed by bias , a skewed significance level from polling the wrong people, or only a vague idea of what your customer would actually pay for your product. 

A template will help keep your hypothesis on track by standardizing the structure of the hypothesis so that each new hypothesis always includes the specifics of your client personas, the cost of your product, and client or customer pain points. 

A value hypothesis template might look like: 

[Client] will spend [cost] to purchase and use our [title of product/service] to solve their [specific problem] OR help them overcome [specific obstacle]. 

An example of your hypothesis might look like: 

B2B startups will spend $500/mo to purchase our resource planning software to solve resource over-allocation and employee burnout.

By organizing your ideas and the important elements (who, what, where, when, and why), you can come up with a hypothesis that actually answers the question of whether your product is useful and valuable to your ideal customer. 

2. Turn Customer Feedback into Data to Support Your Hypothesis  

Once you have your hypothesis, it’s time to figure out whether it’s true—or, more accurately, prove that it’s valid. Since a hypothesis is never considered “100% proven,” it’s referred to as either valid or invalid based on the information you discover in your experiments or tests. Additionally, your results could lead to an alternative hypothesis, which is helpful in refining your core idea.

To support value hypothesis testing, you need data. To do that, you'll want to collect customer feedback . A customer feedback management tool can also make it easier for your team to access the feedback and create strategies to implement or improve customer concerns. 

If you find that potential clients are not expressing pain points that could be solved with your product or you’re not seeing an interest in the features you hope to add, you can adjust your hypothesis and absorb a lower risk. Because you didn’t invest a lot of time and money into creating the product yet, you should have more resources to put toward the product once you work out the kinks. 

On the other hand, if you find that customers are requesting features your product offers or pain points your product could solve, then you can move forward with product development, confident that your future customers will value (and spend money on) the product you’re creating. 

A customer feedback management tool like UserVoice can empower you to challenge assumptions from your colleagues (often based on anecdotal information) which find their way into team decision making . Having data to reevaluate an assumption helps with prioritization, and it confirms that you’re focusing on the right things as an organization.

3. Validate Your Product 

Since you have a clear idea of who your ideal customer is at this point and have verified their need for your product, it’s time to validate your product and decide if it’s better than your competitors’. 

At this point, simply asking your customers if they would buy your product (or spend more on your product) instead of a competitor’s isn’t enough confirmation that you should move forward, and customers may be biased or reluctant to provide critical feedback. 

Instead, create a minimum viable product (MVP). An MVP is a working, bare-bones version of the product that you can test out without risking your whole budget. Hypothesis testing with an MVP simulates the product experience for customers and, based on their actions and usage, validates that the full product will generate revenue and be successful.  

If you take the steps to first verify and then validate your hypothesis using data, your product is more likely to do well. Your focus will be on the aspect that matters most—whether your customer actually wants and would invest money in purchasing the product.

4. Use Safeguards to Remain Objective 

One of the pitfalls of believing in your product and attempting to validate it is that you’re subject to confirmation bias . Because you want your product to succeed, you may pay more attention to the answers in the collected data that affirm the value of your product and gloss over the information that may lead you to conclude that your hypothesis is actually false. Confirmation bias could easily cloud your vision or skew your metrics without you even realizing it. 

Since it’s hard to know when you’re engaging in confirmation bias, it’s good to have safeguards in place to keep you in check and aligned with the purpose of objectively evaluating your value hypothesis. 

Safeguards include sharing your findings with third-party experts or simply putting yourself in the customer’s shoes.

Third-party experts are the business version of seeking a peer review. External parties don’t stand to benefit from the outcome of your verification and validation process, so your work is verified and validated objectively. You gain the benefit of knowing whether your hypothesis is valid in the eyes of the people who aren’t stakeholders without the risk of confirmation bias. 

In addition to seeking out objective minds, look into potential counter-arguments , such as customer objections (explicit or imagined). What might your customer think about investing the time to learn how to use your product? Will they think the value is commensurate with the monetary cost of the product? 

When running an experiment on validating your hypothesis, it’s important not to elevate the importance of your beliefs over the objective data you collect. While it can be exciting to push for the validity of your idea, it can lead to false assumptions and the permission of weak evidence. 

Validation Is the Key to Product Success

With your new value hypothesis in hand, you can confidently move forward, knowing that there’s a true need, desire, and market for your product.

Because you’ve verified and validated your guesses, there’s less of a chance that you’re wrong about the value of your product, and there are fewer financial and resource risks for your company. With this strong foundation and the new information you’ve uncovered about your customers, you can add even more value to your product or use it to make more products that fit the market and user needs. 

If you think customer feedback management software would be useful in your hypothesis validation process, consider opting into our free trial to see how UserVoice can help.

Heather Tipton

Start your free trial.

Tips to Create and Test a Value Hypothesis: A Step-by-Step Guide

Developing a robust value hypothesis is crucial as you bring a new product to market, guiding your startup toward answering a genuine market need. Constructing a verifiable value hypothesis anchors your product's development process in customer feedback and data-driven insight rather than assumptions.

This framework enables you to clarify the potential value your product offers and provides a foundation for testing and refining your approach, significantly reducing the risk of misalignment with your target market. To set the stage for success, employ logical structures and objective measures, such as creating a minimum viable product, to effectively validate your product's value proposition.

What Is a Verifiable Value Hypothesis?

A verifiable value hypothesis articulates your belief about how your product will deliver value to customers. It is a testable prediction aimed at demonstrating the expected outcomes for your target market.

To ensure that your value hypothesis is verifiable, it should adhere to the following conditions:

• Specific : Clearly defines the value proposition and the customer segment.
• Measurable : Includes metrics by which you can assess success or failure.
• Achievable : Realistic based on your resources and market conditions.
• Relevant : Directly addresses a significant customer need or desire.
• Time-Bound : Has a defined period for testing and validation.

When you create a value hypothesis, you're essentially forming the backbone of your business model. It goes beyond a mere assumption and relies on customer feedback data to inform its development. You also safeguard it with objective measures, such as a minimum viable product, to test the hypothesis in real life.

By articulating and examining a verifiable value hypothesis, you understand your product's potential impact and reduce the risk associated with new product development. It's about making informed decisions that increase your confidence in the product's potential success before committing significant resources.

Value Hypotheses vs. Growth Hypotheses

Value hypotheses and growth hypotheses are two distinct concepts often used in business, especially in the context of startups and product development.

Value Hypotheses : A value hypothesis is centered around the product itself. It focuses on whether the product truly delivers customer value. Key questions include whether the product meets a real need, how it compares to alternatives, and if customers are willing to pay for it. Valuing a value hypothesis is crucial before a business scales its operations.

Growth Hypotheses : A growth hypothesis, on the other hand, deals with the scalability and marketing aspects of the business. It involves strategies and channels used to acquire new customers. The focus is on how to grow the customer base, the cost-effectiveness of growth strategies, and the sustainability of growth. Validating a growth hypothesis is typically the next step after confirming that the product has value to the customers.

In practice, both hypotheses are crucial for the success of a business. A value hypothesis ensures the product is desirable and needed, while a growth hypothesis ensures that the product can reach a larger market effectively.

Tips to Create and Test a Verifiable Value Hypothesis

Creating a value hypothesis is crucial for understanding what drives customer interest in your product. It's an educated guess that requires rigor to define and clarity to test. When developing a value hypothesis, you're attempting to validate assumptions about your product's value to customers. Here are concise tips to help you with this process:

1. Understanding Your Market and Customers

Before formulating a hypothesis, you need a deep understanding of your market and potential customers. You're looking to uncover their pain points and needs which your product aims to address.

Begin with thorough market research and collect customer feedback to ensure your idea is built upon a solid foundation of real-world insights. This understanding is pivotal as it sets the tone for a relevant and testable hypothesis.

• Define Your Value Proposition Clearly: Articulate your product's value to the user. What problem does it solve? How does it improve the user's life or work?
• Identify Your Target Audience. Determine who your ideal customers are. Understand their needs, pain points, and how they currently address the problem your product intends to solve.

2. Defining Clear Assumptions

The next step is to outline clear assumptions based on your idea that you believe will bring value to your customers. Each assumption should be an assertion that directly relates to how your customers will find your product valuable.

For example, if your product is a task management app, you might assume that the ability to share task lists with team members is a pain point for your potential customers. Remember, assumptions are not facts—they are educated guesses that need verification.

3. Identify Key Metrics for Your Hypothesis Test

Once you've defined your assumptions, delineate the framework for testing your value hypothesis. This involves designing experiments that validate or invalidate your assumptions with measurable outcomes. Ensure that your hypothesis can be tested with measurable outcomes. This could be in the form of user engagement metrics, conversion rates, or customer satisfaction scores.

Determine what success looks like and define objective metrics that will prove your product's value. This could be user engagement, conversion rates, or revenue. Choosing the right metrics is essential for an accurate test. For instance, in your test, you might measure the increase in customer retention or the decrease in time spent on task organization with your app. Construct your test so that the results are unequivocal and actionable.

4. Construct a Testable Proposition

Formulate your hypothesis in a way that can be tested empirically. Use qualitative research methods such as interviews, surveys, and observation to gather data about your potential users. Formulate your value hypothesis based on insights from this research. Plan experiments that can validate or invalidate your value hypothesis. This might involve A/B testing, user testing sessions, or pilot programs.

A good example is to posit that "Introducing feature X will increase user onboarding by Y%." Avoid complexity by testing one variable simultaneously. This helps you identify which changes are actually making a difference.

5. Applying Evidence to Innovation

When your data indicates a promising avenue for product development , it's imperative that you validate your growth hypothesis through experimentation. Align your value proposition with the evidence at hand.

Develop a simplified version of your product that allows you to test the core value proposition with real users without investing in full-scale production. Start by crafting a minimum viable product ( MVP ) to begin testing in the market. This approach helps mitigate risk by not investing heavily in unproven ideas. Use analytics tools to collect data on how users interact with your MVP. Look for patterns that either support or contradict your value hypothesis.

If the data suggests that your value hypothesis is wrong, be prepared to revise your hypothesis or pivot your product strategy accordingly.

6. Gather Customer Feedback

Integrating customer feedback into your product development process can create a more tailored value proposition. This step is crucial in refining your product to meet user needs and validate your hypotheses.

Use customer feedback tools to collect data on how users interact with your MVP. Look for patterns that either support or contradict your value hypothesis. Here are some ways to collect feedback effectively :

• Feedback portals
• User testing sessions
• In-app feedback
• Website widgets
• Direct interviews
• Focus groups
• Feedback forums

Create a centralized place for product feedback to keep track of different types of customer feedback and improve SaaS products while listening to their customers. Rapidr helps companies be more customer-centric by consolidating feedback across different apps, prioritizing requests, having a discourse with customers, and closing the feedback loop.

7. Analyze and Iterate Quickly

Review the data and analyze customer feedback to see if it supports your hypothesis. If your hypothesis is not supported, iterate on your assumptions, and test again. Keep a detailed record of your hypotheses, experiments, and findings. This documentation will help you understand the evolution of your product and guide future decision-making.

Use the feedback and data from your tests to make quick iterations of your product and drive product development . This allows you to refine your value proposition and improve the fit with your target audience. Engage with your users throughout the process. Real-world feedback is invaluable and can provide insights that data alone cannot.

• Identify Patterns : What commonalities are present in the feedback?
• Implement Changes : Prioritize and make adjustments based on customer insights.

9. Align with Business Goals and Stay Customer-Focused

Ensure that your value hypothesis aligns with the broader goals of your business. The value provided should ultimately contribute to the success of the company. Remember that the ultimate goal of your value hypothesis is to deliver something that customers find valuable. Maintain a strong focus on customer needs and satisfaction throughout the process.

10. Communicate with Stakeholders and Update them

Keep all stakeholders informed about your findings and the implications for the product. Clear communication helps ensure everyone is aligned and understands the rationale behind product decisions. Communicate and close the feedback loop with the help of a product changelog through which you can ​​announce new changes and engage with customers.

Understanding and validating a value hypothesis is essential for any business, particularly startups. It involves deeply exploring whether a product or service meets customer needs and offers real value. This process ensures that resources are invested in desirable and useful products, and it's a critical step before considering scalability and growth.

By focusing on the value hypothesis, businesses can better align their offerings with market demand, leading to more sustainable success. Placing customer feedback at the center of the process of testing a value hypothesis helps you develop a product that meets your customers' needs and stands out in the market.

Rapidr helps companies be more customer-centric by consolidating feedback across different apps, prioritizing requests, having a discourse with customers, and closing the feedback loop.

Build better products with user feedback

Rapidr helps SaaS companies understand what customers need through feedback, prioritize what to build next, inform the roadmap, and notify customers on product releases

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.6: Test of Mean vs. Hypothesized Value – A Complete Example

• Last updated
• Save as PDF
• Page ID 20909

• Maurice A. Geraghty
• De Anza College

Example – Soy sauce production

A food company has a policy that the stated contents of a product match the actual results. A General Question might be “Does the stated net weight of a food product match the actual weight?” The quality control statistician decides to test the 16 ounce bottle of Soy Sauce and must now design the experiment .

The quality‐control statistician has been given the authority to sample 36 bottles of soy sauce and knows from past testing that the population standard deviation is 0.5 ounces. The model will be a test of population mean vs. hypothesized value of 16 oz.  A two‐tailed test is selected since the company is concerned about both overfilling and underfilling the bottles as the stated policy is that the stated weight should match the actual weight of the product.

Research Hypotheses :

\(H_o: \mu =16\)  (The filling machine is operating properly)                                          

\(H_a: \mu \neq 16\) (The filling machine is not operating properly)

Since the population standard deviation is known the test statistic will be \(Z=\dfrac{\overline{X}-\mu}{\sigma / \sqrt{n}}\). This model is appropriate since the sample size assures that the distribution of the sample mean is approximately Normal due to the Central Limit Theorem.

Type I error would be to reject the Null Hypothesis and say that the machine is not running properly when in fact it was operating properly. Since the company does not want to needlessly stop production and recalibrate the machine, the statistician chooses to limit the probability of Type I error by setting the level of significance (\(\alpha\)) to 5%.

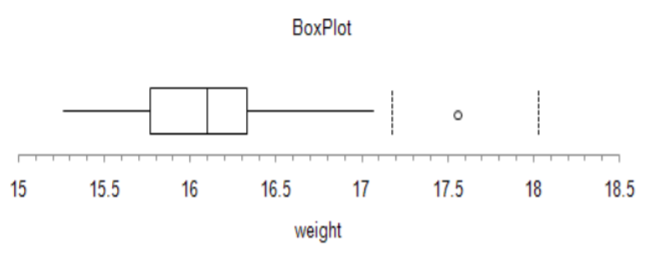
The statistician now conducts the experiment and samples 36 bottles over one hour and determines from a box plot of the data that there is one unusual observation of 17.56 ounces. The value is rechecked and kept in the data set.

Next, the sample mean and the test statistic are calculated.

\[\overline{X}=16.12 \text { ounces } \qquad \qquad Z=\dfrac{16.12-16}{0.5 / \sqrt{36}}=1.44 \nonumber \]

The decision rule under the critical value method would be to reject the Null Hypothesis when the value of the test statistic is in the rejection region. In other words, reject \(H_o\) when \(Z >1.96\) or \(Z<‐1.96\).

Based on this result, the decision is fail to reject \(H_o\) , since the test statistic does not fall in the rejection region.

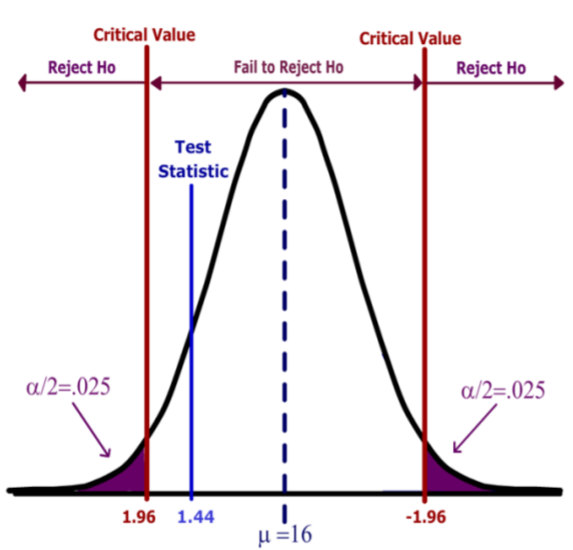
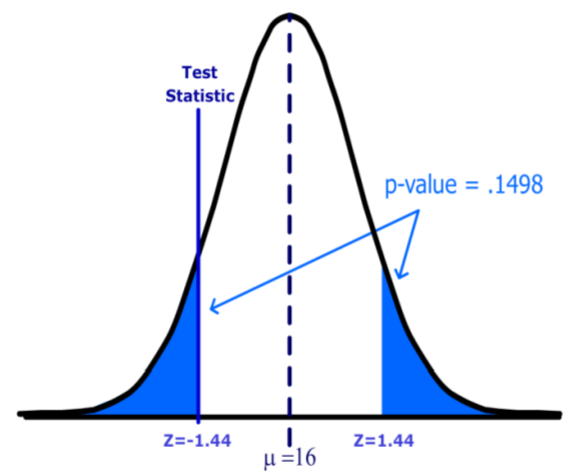
Alternatively (and preferably) the statistician could use the p‐value method of decision rule. The \(p\)‐value for a two‐tailed test must include all values (positive and negative) more extreme than the Test Statistic, so in this example we find the probability that \(Z < ‐1.44\) or \(Z > 1.44\) (the area shaded blue).

Using a calculator, computer software or a Standard Normal table, the \(p\)‐value=0.1498 . Since the \(p\)‐value is greater than \(\alpha\) the decision again is fail to reject \(H_o\) .

Finally the statistician must report the conclusions and make a recommendation to the company’s management:

“There is insufficient evidence to conclude that the machine that fills 16 ounce soy sauce bottles is operating improperly. This conclusion is based on 36 measurements taken during a single hour’s production run. I recommend continued monitoring of the machine during different employee shifts to account for the possibility of potential human error”.

The statistician makes the weak statement and is not stating that the machine is running properly, only that there is not enough evidence to state that the machine is running improperly. The statistician also reports concerns about the sampling of only one shift of employees (restricting the inference to the sampled population) and recommends repeating the experiment over several shifts.

p-value Calculator

What is p-value, how do i calculate p-value from test statistic, how to interpret p-value, how to use the p-value calculator to find p-value from test statistic, how do i find p-value from z-score, how do i find p-value from t, p-value from chi-square score (χ² score), p-value from f-score.

Welcome to our p-value calculator! You will never again have to wonder how to find the p-value, as here you can determine the one-sided and two-sided p-values from test statistics, following all the most popular distributions: normal, t-Student, chi-squared, and Snedecor's F.

P-values appear all over science, yet many people find the concept a bit intimidating. Don't worry – in this article, we will explain not only what the p-value is but also how to interpret p-values correctly . Have you ever been curious about how to calculate the p-value by hand? We provide you with all the necessary formulae as well!

🙋 If you want to revise some basics from statistics, our normal distribution calculator is an excellent place to start.

Formally, the p-value is the probability that the test statistic will produce values at least as extreme as the value it produced for your sample . It is crucial to remember that this probability is calculated under the assumption that the null hypothesis H 0 is true !

More intuitively, p-value answers the question:

Assuming that I live in a world where the null hypothesis holds, how probable is it that, for another sample, the test I'm performing will generate a value at least as extreme as the one I observed for the sample I already have?

It is the alternative hypothesis that determines what "extreme" actually means , so the p-value depends on the alternative hypothesis that you state: left-tailed, right-tailed, or two-tailed. In the formulas below, S stands for a test statistic, x for the value it produced for a given sample, and Pr(event | H 0 ) is the probability of an event, calculated under the assumption that H 0 is true:

Left-tailed test: p-value = Pr(S ≤ x | H 0 )

Right-tailed test: p-value = Pr(S ≥ x | H 0 )

Two-tailed test:

p-value = 2 × min{Pr(S ≤ x | H 0 ), Pr(S ≥ x | H 0 )}

(By min{a,b} , we denote the smaller number out of a and b .)

If the distribution of the test statistic under H 0 is symmetric about 0 , then: p-value = 2 × Pr(S ≥ |x| | H 0 )

or, equivalently: p-value = 2 × Pr(S ≤ -|x| | H 0 )

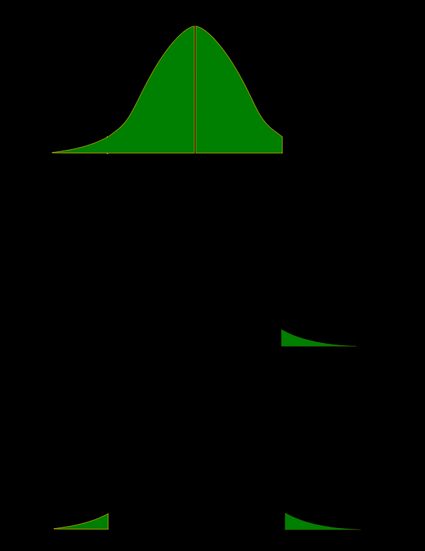
As a picture is worth a thousand words, let us illustrate these definitions. Here, we use the fact that the probability can be neatly depicted as the area under the density curve for a given distribution. We give two sets of pictures: one for a symmetric distribution and the other for a skewed (non-symmetric) distribution.

• Symmetric case: normal distribution:

• Non-symmetric case: chi-squared distribution:

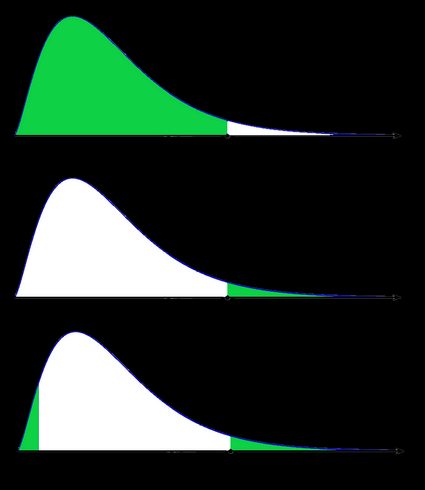
In the last picture (two-tailed p-value for skewed distribution), the area of the left-hand side is equal to the area of the right-hand side.

To determine the p-value, you need to know the distribution of your test statistic under the assumption that the null hypothesis is true . Then, with the help of the cumulative distribution function ( cdf ) of this distribution, we can express the probability of the test statistics being at least as extreme as its value x for the sample:

Left-tailed test:

p-value = cdf(x) .

Right-tailed test:

p-value = 1 - cdf(x) .

p-value = 2 × min{cdf(x) , 1 - cdf(x)} .

If the distribution of the test statistic under H 0 is symmetric about 0 , then a two-sided p-value can be simplified to p-value = 2 × cdf(-|x|) , or, equivalently, as p-value = 2 - 2 × cdf(|x|) .

The probability distributions that are most widespread in hypothesis testing tend to have complicated cdf formulae, and finding the p-value by hand may not be possible. You'll likely need to resort to a computer or to a statistical table, where people have gathered approximate cdf values.

Well, you now know how to calculate the p-value, but… why do you need to calculate this number in the first place? In hypothesis testing, the p-value approach is an alternative to the critical value approach . Recall that the latter requires researchers to pre-set the significance level, α, which is the probability of rejecting the null hypothesis when it is true (so of type I error ). Once you have your p-value, you just need to compare it with any given α to quickly decide whether or not to reject the null hypothesis at that significance level, α. For details, check the next section, where we explain how to interpret p-values.

As we have mentioned above, the p-value is the answer to the following question:

What does that mean for you? Well, you've got two options:

• A high p-value means that your data is highly compatible with the null hypothesis; and
• A small p-value provides evidence against the null hypothesis , as it means that your result would be very improbable if the null hypothesis were true.

However, it may happen that the null hypothesis is true, but your sample is highly unusual! For example, imagine we studied the effect of a new drug and got a p-value of 0.03 . This means that in 3% of similar studies, random chance alone would still be able to produce the value of the test statistic that we obtained, or a value even more extreme, even if the drug had no effect at all!

The question "what is p-value" can also be answered as follows: p-value is the smallest level of significance at which the null hypothesis would be rejected. So, if you now want to make a decision on the null hypothesis at some significance level α , just compare your p-value with α :

• If p-value ≤ α , then you reject the null hypothesis and accept the alternative hypothesis; and
• If p-value ≥ α , then you don't have enough evidence to reject the null hypothesis.

Obviously, the fate of the null hypothesis depends on α . For instance, if the p-value was 0.03 , we would reject the null hypothesis at a significance level of 0.05 , but not at a level of 0.01 . That's why the significance level should be stated in advance and not adapted conveniently after the p-value has been established! A significance level of 0.05 is the most common value, but there's nothing magical about it. Here, you can see what too strong a faith in the 0.05 threshold can lead to. It's always best to report the p-value, and allow the reader to make their own conclusions.

Also, bear in mind that subject area expertise (and common reason) is crucial. Otherwise, mindlessly applying statistical principles, you can easily arrive at statistically significant, despite the conclusion being 100% untrue.

As our p-value calculator is here at your service, you no longer need to wonder how to find p-value from all those complicated test statistics! Here are the steps you need to follow:

Pick the alternative hypothesis : two-tailed, right-tailed, or left-tailed.

Tell us the distribution of your test statistic under the null hypothesis: is it N(0,1), t-Student, chi-squared, or Snedecor's F? If you are unsure, check the sections below, as they are devoted to these distributions.

If needed, specify the degrees of freedom of the test statistic's distribution.

Enter the value of test statistic computed for your data sample.

Our calculator determines the p-value from the test statistic and provides the decision to be made about the null hypothesis. The standard significance level is 0.05 by default.

Go to the advanced mode if you need to increase the precision with which the calculations are performed or change the significance level .

In terms of the cumulative distribution function (cdf) of the standard normal distribution, which is traditionally denoted by Φ , the p-value is given by the following formulae:

Left-tailed z-test:

p-value = Φ(Z score )

Right-tailed z-test:

p-value = 1 - Φ(Z score )

Two-tailed z-test:

p-value = 2 × Φ(−|Z score |)

p-value = 2 - 2 × Φ(|Z score |)

🙋 To learn more about Z-tests, head to Omni's Z-test calculator .

We use the Z-score if the test statistic approximately follows the standard normal distribution N(0,1) . Thanks to the central limit theorem, you can count on the approximation if you have a large sample (say at least 50 data points) and treat your distribution as normal.

A Z-test most often refers to testing the population mean , or the difference between two population means, in particular between two proportions. You can also find Z-tests in maximum likelihood estimations.

The p-value from the t-score is given by the following formulae, in which cdf t,d stands for the cumulative distribution function of the t-Student distribution with d degrees of freedom:

Left-tailed t-test:

p-value = cdf t,d (t score )

Right-tailed t-test:

p-value = 1 - cdf t,d (t score )

Two-tailed t-test:

p-value = 2 × cdf t,d (−|t score |)

p-value = 2 - 2 × cdf t,d (|t score |)

Use the t-score option if your test statistic follows the t-Student distribution . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails – the exact shape depends on the parameter called the degrees of freedom . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from the normal distribution N(0,1).

The most common t-tests are those for population means with an unknown population standard deviation, or for the difference between means of two populations , with either equal or unequal yet unknown population standard deviations. There's also a t-test for paired (dependent) samples .

🙋 To get more insights into t-statistics, we recommend using our t-test calculator .

Use the χ²-score option when performing a test in which the test statistic follows the χ²-distribution .

This distribution arises if, for example, you take the sum of squared variables, each following the normal distribution N(0,1). Remember to check the number of degrees of freedom of the χ²-distribution of your test statistic!

How to find the p-value from chi-square-score ? You can do it with the help of the following formulae, in which cdf χ²,d denotes the cumulative distribution function of the χ²-distribution with d degrees of freedom:

Left-tailed χ²-test:

p-value = cdf χ²,d (χ² score )

Right-tailed χ²-test:

p-value = 1 - cdf χ²,d (χ² score )

Remember that χ²-tests for goodness-of-fit and independence are right-tailed tests! (see below)

Two-tailed χ²-test:

p-value = 2 × min{cdf χ²,d (χ² score ), 1 - cdf χ²,d (χ² score )}

(By min{a,b} , we denote the smaller of the numbers a and b .)

The most popular tests which lead to a χ²-score are the following:

Testing whether the variance of normally distributed data has some pre-determined value. In this case, the test statistic has the χ²-distribution with n - 1 degrees of freedom, where n is the sample size. This can be a one-tailed or two-tailed test .

Goodness-of-fit test checks whether the empirical (sample) distribution agrees with some expected probability distribution. In this case, the test statistic follows the χ²-distribution with k - 1 degrees of freedom, where k is the number of classes into which the sample is divided. This is a right-tailed test .

Independence test is used to determine if there is a statistically significant relationship between two variables. In this case, its test statistic is based on the contingency table and follows the χ²-distribution with (r - 1)(c - 1) degrees of freedom, where r is the number of rows, and c is the number of columns in this contingency table. This also is a right-tailed test .

Finally, the F-score option should be used when you perform a test in which the test statistic follows the F-distribution , also known as the Fisher–Snedecor distribution. The exact shape of an F-distribution depends on two degrees of freedom .

To see where those degrees of freedom come from, consider the independent random variables X and Y , which both follow the χ²-distributions with d 1 and d 2 degrees of freedom, respectively. In that case, the ratio (X/d 1 )/(Y/d 2 ) follows the F-distribution, with (d 1 , d 2 ) -degrees of freedom. For this reason, the two parameters d 1 and d 2 are also called the numerator and denominator degrees of freedom .

The p-value from F-score is given by the following formulae, where we let cdf F,d1,d2 denote the cumulative distribution function of the F-distribution, with (d 1 , d 2 ) -degrees of freedom:

Left-tailed F-test:

p-value = cdf F,d1,d2 (F score )

Right-tailed F-test:

p-value = 1 - cdf F,d1,d2 (F score )

Two-tailed F-test:

p-value = 2 × min{cdf F,d1,d2 (F score ), 1 - cdf F,d1,d2 (F score )}

Below we list the most important tests that produce F-scores. All of them are right-tailed tests .

A test for the equality of variances in two normally distributed populations . Its test statistic follows the F-distribution with (n - 1, m - 1) -degrees of freedom, where n and m are the respective sample sizes.

ANOVA is used to test the equality of means in three or more groups that come from normally distributed populations with equal variances. We arrive at the F-distribution with (k - 1, n - k) -degrees of freedom, where k is the number of groups, and n is the total sample size (in all groups together).

A test for overall significance of regression analysis . The test statistic has an F-distribution with (k - 1, n - k) -degrees of freedom, where n is the sample size, and k is the number of variables (including the intercept).

With the presence of the linear relationship having been established in your data sample with the above test, you can calculate the coefficient of determination, R 2 , which indicates the strength of this relationship . You can do it by hand or use our coefficient of determination calculator .

A test to compare two nested regression models . The test statistic follows the F-distribution with (k 2 - k 1 , n - k 2 ) -degrees of freedom, where k 1 and k 2 are the numbers of variables in the smaller and bigger models, respectively, and n is the sample size.

You may notice that the F-test of an overall significance is a particular form of the F-test for comparing two nested models: it tests whether our model does significantly better than the model with no predictors (i.e., the intercept-only model).

Can p-value be negative?

No, the p-value cannot be negative. This is because probabilities cannot be negative, and the p-value is the probability of the test statistic satisfying certain conditions.

What does a high p-value mean?

A high p-value means that under the null hypothesis, there's a high probability that for another sample, the test statistic will generate a value at least as extreme as the one observed in the sample you already have. A high p-value doesn't allow you to reject the null hypothesis.

What does a low p-value mean?

A low p-value means that under the null hypothesis, there's little probability that for another sample, the test statistic will generate a value at least as extreme as the one observed for the sample you already have. A low p-value is evidence in favor of the alternative hypothesis – it allows you to reject the null hypothesis.

5 number summary

Chilled drink, standard error.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (570)
• Health (440)
• Physics (510)
• Sports (105)
• Statistics (182)
• Other (182)
• Discover Omni (40)

An official website of the United States government

The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings
• Browse Titles

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].

Hypothesis testing, p values, confidence intervals, and significance.

Jacob Shreffler ; Martin R. Huecker .

Affiliations

Last Update: March 13, 2023 .

• Definition/Introduction

Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting these findings, which may affect the adequate application of the data.

• Issues of Concern

Without a foundational understanding of hypothesis testing, p values, confidence intervals, and the difference between statistical and clinical significance, it may affect healthcare providers' ability to make clinical decisions without relying purely on the research investigators deemed level of significance. Therefore, an overview of these concepts is provided to allow medical professionals to use their expertise to determine if results are reported sufficiently and if the study outcomes are clinically appropriate to be applied in healthcare practice.

Hypothesis Testing

Investigators conducting studies need research questions and hypotheses to guide analyses. Starting with broad research questions (RQs), investigators then identify a gap in current clinical practice or research. Any research problem or statement is grounded in a better understanding of relationships between two or more variables. For this article, we will use the following research question example:

Research Question: Is Drug 23 an effective treatment for Disease A?

Research questions do not directly imply specific guesses or predictions; we must formulate research hypotheses. A hypothesis is a predetermined declaration regarding the research question in which the investigator(s) makes a precise, educated guess about a study outcome. This is sometimes called the alternative hypothesis and ultimately allows the researcher to take a stance based on experience or insight from medical literature. An example of a hypothesis is below.

Research Hypothesis: Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22.

The null hypothesis states that there is no statistical difference between groups based on the stated research hypothesis.

Researchers should be aware of journal recommendations when considering how to report p values, and manuscripts should remain internally consistent.

Regarding p values, as the number of individuals enrolled in a study (the sample size) increases, the likelihood of finding a statistically significant effect increases. With very large sample sizes, the p-value can be very low significant differences in the reduction of symptoms for Disease A between Drug 23 and Drug 22. The null hypothesis is deemed true until a study presents significant data to support rejecting the null hypothesis. Based on the results, the investigators will either reject the null hypothesis (if they found significant differences or associations) or fail to reject the null hypothesis (they could not provide proof that there were significant differences or associations).

To test a hypothesis, researchers obtain data on a representative sample to determine whether to reject or fail to reject a null hypothesis. In most research studies, it is not feasible to obtain data for an entire population. Using a sampling procedure allows for statistical inference, though this involves a certain possibility of error. [1]  When determining whether to reject or fail to reject the null hypothesis, mistakes can be made: Type I and Type II errors. Though it is impossible to ensure that these errors have not occurred, researchers should limit the possibilities of these faults. [2]

Significance

Significance is a term to describe the substantive importance of medical research. Statistical significance is the likelihood of results due to chance. [3]  Healthcare providers should always delineate statistical significance from clinical significance, a common error when reviewing biomedical research. [4]  When conceptualizing findings reported as either significant or not significant, healthcare providers should not simply accept researchers' results or conclusions without considering the clinical significance. Healthcare professionals should consider the clinical importance of findings and understand both p values and confidence intervals so they do not have to rely on the researchers to determine the level of significance. [5]  One criterion often used to determine statistical significance is the utilization of p values.

P values are used in research to determine whether the sample estimate is significantly different from a hypothesized value. The p-value is the probability that the observed effect within the study would have occurred by chance if, in reality, there was no true effect. Conventionally, data yielding a p<0.05 or p<0.01 is considered statistically significant. While some have debated that the 0.05 level should be lowered, it is still universally practiced. [6]  Hypothesis testing allows us to determine the size of the effect.

An example of findings reported with p values are below:

Statement: Drug 23 reduced patients' symptoms compared to Drug 22. Patients who received Drug 23 (n=100) were 2.1 times less likely than patients who received Drug 22 (n = 100) to experience symptoms of Disease A, p<0.05.

Statement:Individuals who were prescribed Drug 23 experienced fewer symptoms (M = 1.3, SD = 0.7) compared to individuals who were prescribed Drug 22 (M = 5.3, SD = 1.9). This finding was statistically significant, p= 0.02.

For either statement, if the threshold had been set at 0.05, the null hypothesis (that there was no relationship) should be rejected, and we should conclude significant differences. Noticeably, as can be seen in the two statements above, some researchers will report findings with < or > and others will provide an exact p-value (0.000001) but never zero [6] . When examining research, readers should understand how p values are reported. The best practice is to report all p values for all variables within a study design, rather than only providing p values for variables with significant findings. [7]  The inclusion of all p values provides evidence for study validity and limits suspicion for selective reporting/data mining.  

While researchers have historically used p values, experts who find p values problematic encourage the use of confidence intervals. [8] . P-values alone do not allow us to understand the size or the extent of the differences or associations. [3]  In March 2016, the American Statistical Association (ASA) released a statement on p values, noting that scientific decision-making and conclusions should not be based on a fixed p-value threshold (e.g., 0.05). They recommend focusing on the significance of results in the context of study design, quality of measurements, and validity of data. Ultimately, the ASA statement noted that in isolation, a p-value does not provide strong evidence. [9]

When conceptualizing clinical work, healthcare professionals should consider p values with a concurrent appraisal study design validity. For example, a p-value from a double-blinded randomized clinical trial (designed to minimize bias) should be weighted higher than one from a retrospective observational study [7] . The p-value debate has smoldered since the 1950s [10] , and replacement with confidence intervals has been suggested since the 1980s. [11]

Confidence Intervals

A confidence interval provides a range of values within given confidence (e.g., 95%), including the accurate value of the statistical constraint within a targeted population. [12]  Most research uses a 95% CI, but investigators can set any level (e.g., 90% CI, 99% CI). [13]  A CI provides a range with the lower bound and upper bound limits of a difference or association that would be plausible for a population. [14]  Therefore, a CI of 95% indicates that if a study were to be carried out 100 times, the range would contain the true value in 95, [15]  confidence intervals provide more evidence regarding the precision of an estimate compared to p-values. [6]

In consideration of the similar research example provided above, one could make the following statement with 95% CI:

Statement: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22; there was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

It is important to note that the width of the CI is affected by the standard error and the sample size; reducing a study sample number will result in less precision of the CI (increase the width). [14]  A larger width indicates a smaller sample size or a larger variability. [16]  A researcher would want to increase the precision of the CI. For example, a 95% CI of 1.43 – 1.47 is much more precise than the one provided in the example above. In research and clinical practice, CIs provide valuable information on whether the interval includes or excludes any clinically significant values. [14]

Null values are sometimes used for differences with CI (zero for differential comparisons and 1 for ratios). However, CIs provide more information than that. [15]  Consider this example: A hospital implements a new protocol that reduced wait time for patients in the emergency department by an average of 25 minutes (95% CI: -2.5 – 41 minutes). Because the range crosses zero, implementing this protocol in different populations could result in longer wait times; however, the range is much higher on the positive side. Thus, while the p-value used to detect statistical significance for this may result in "not significant" findings, individuals should examine this range, consider the study design, and weigh whether or not it is still worth piloting in their workplace.

Similarly to p-values, 95% CIs cannot control for researchers' errors (e.g., study bias or improper data analysis). [14]  In consideration of whether to report p-values or CIs, researchers should examine journal preferences. When in doubt, reporting both may be beneficial. [13]  An example is below:

Reporting both: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22, p = 0.009. There was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

• Clinical Significance

Recall that clinical significance and statistical significance are two different concepts. Healthcare providers should remember that a study with statistically significant differences and large sample size may be of no interest to clinicians, whereas a study with smaller sample size and statistically non-significant results could impact clinical practice. [14]  Additionally, as previously mentioned, a non-significant finding may reflect the study design itself rather than relationships between variables.

Healthcare providers using evidence-based medicine to inform practice should use clinical judgment to determine the practical importance of studies through careful evaluation of the design, sample size, power, likelihood of type I and type II errors, data analysis, and reporting of statistical findings (p values, 95% CI or both). [4]  Interestingly, some experts have called for "statistically significant" or "not significant" to be excluded from work as statistical significance never has and will never be equivalent to clinical significance. [17]

The decision on what is clinically significant can be challenging, depending on the providers' experience and especially the severity of the disease. Providers should use their knowledge and experiences to determine the meaningfulness of study results and make inferences based not only on significant or insignificant results by researchers but through their understanding of study limitations and practical implications.

• Nursing, Allied Health, and Interprofessional Team Interventions

All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts in this chapter. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care. 

• Review Questions
• Access free multiple choice questions on this topic.
• Comment on this article.

Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.

Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

• Cite this Page Shreffler J, Huecker MR. Hypothesis Testing, P Values, Confidence Intervals, and Significance. [Updated 2023 Mar 13]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

• Bulk download StatPearls data from FTP

Related information

• PMC PubMed Central citations
• PubMed Links to PubMed

Similar articles in PubMed

• The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). [PeerJ. 2021] The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). Messam LLM, Weng HY, Rosenberger NWY, Tan ZH, Payet SDM, Santbakshsing M. PeerJ. 2021; 9:e12453. Epub 2021 Nov 24.
• Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. [J Pharm Pract. 2010] Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. Ferrill MJ, Brown DA, Kyle JA. J Pharm Pract. 2010 Aug; 23(4):344-51. Epub 2010 Apr 13.
• Interpreting "statistical hypothesis testing" results in clinical research. [J Ayurveda Integr Med. 2012] Interpreting "statistical hypothesis testing" results in clinical research. Sarmukaddam SB. J Ayurveda Integr Med. 2012 Apr; 3(2):65-9.
• Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. [Dermatol Surg. 2005] Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. Alam M, Barzilai DA, Wrone DA. Dermatol Surg. 2005 Apr; 31(4):462-6.
• Review Is statistical significance testing useful in interpreting data? [Reprod Toxicol. 1993] Review Is statistical significance testing useful in interpreting data? Savitz DA. Reprod Toxicol. 1993; 7(2):95-100.

Recent Activity

• Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearl... Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.6: Hypothesis Test of a Single Population Mean with Examples

• Last updated
• Save as PDF
• Page ID 130297

Steps for performing Hypothesis Test of a Single Population Mean

Step 1: State your hypotheses about the population mean. Step 2: Summarize the data. State a significance level. State and check conditions required for the procedure

• Find or identify the sample size, n, the sample mean, \(\bar{x}\) and the sample standard deviation, s .

The sampling distribution for the one-mean test statistic is, approximately, T- distribution if the following conditions are met

• Sample is random with independent observations .
• Sample is large. The population must be Normal or the sample size must be at least 30.

Step 3: Perform the procedure based on the assumption that \(H_{0}\) is true

• Find the Estimated Standard Error: \(SE=\frac{s}{\sqrt{n}}\).
• Compute the observed value of the test statistic: \(T_{obs}=\frac{\bar{x}-\mu_{0}}{SE}\).
• Check the type of the test (right-, left-, or two-tailed)
• Find the p-value in order to measure your level of surprise.

Step 4: Make a decision about \(H_{0}\) and \(H_{a}\)

• Do you reject or not reject your null hypothesis?

Step 5: Make a conclusion

• What does this mean in the context of the data?

The following examples illustrate a left-, right-, and two-tailed test.

Example \(\pageindex{1}\).

\(H_{0}: \mu = 5, H_{a}: \mu < 5\)

Test of a single population mean. \(H_{a}\) tells you the test is left-tailed. The picture of the \(p\)-value is as follows:

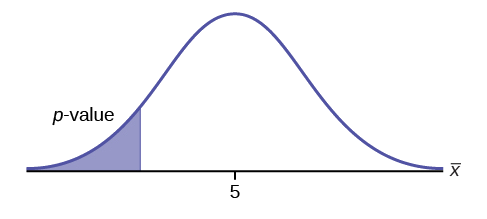
Exercise \(\PageIndex{1}\)

\(H_{0}: \mu = 10, H_{a}: \mu < 10\)

Assume the \(p\)-value is 0.0935. What type of test is this? Draw the picture of the \(p\)-value.

left-tailed test

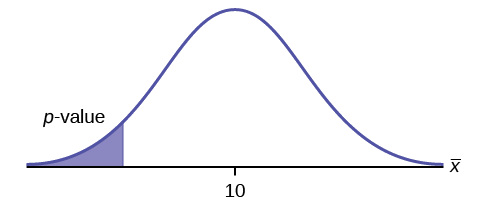
Example \(\PageIndex{2}\)

\(H_{0}: \mu \leq 0.2, H_{a}: \mu > 0.2\)

This is a test of a single population proportion. \(H_{a}\) tells you the test is right-tailed . The picture of the p -value is as follows:

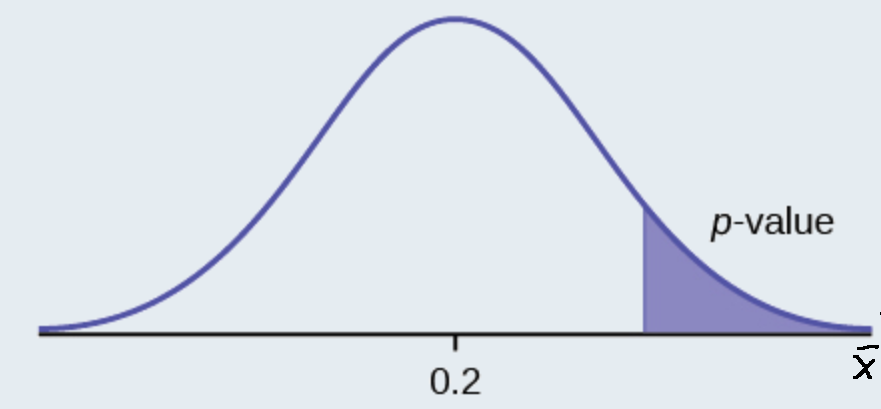
Exercise \(\PageIndex{2}\)

\(H_{0}: \mu \leq 1, H_{a}: \mu > 1\)

Assume the \(p\)-value is 0.1243. What type of test is this? Draw the picture of the \(p\)-value.

right-tailed test

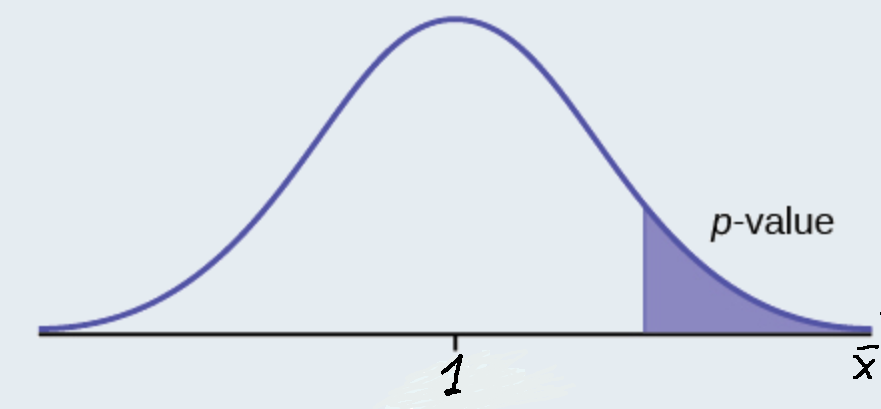
Example \(\PageIndex{3}\)

\(H_{0}: \mu = 50, H_{a}: \mu \neq 50\)

This is a test of a single population mean. \(H_{a}\) tells you the test is two-tailed . The picture of the \(p\)-value is as follows.

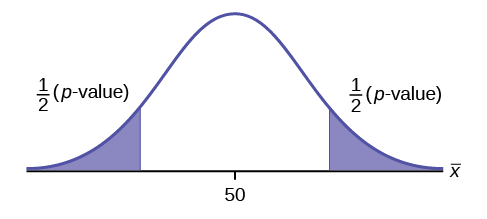
Exercise \(\PageIndex{3}\)

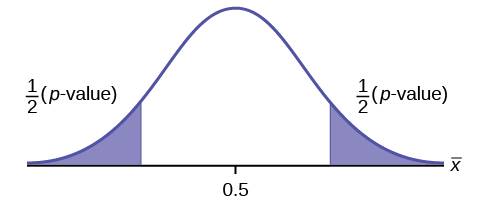
\(H_{0}: \mu = 0.5, H_{a}: \mu \neq 0.5\)

Assume the p -value is 0.2564. What type of test is this? Draw the picture of the \(p\)-value.

two-tailed test

Full Hypothesis Test Examples

Example \(\pageindex{4}\).

Statistics students believe that the mean score on the first statistics test is 65. A statistics instructor thinks the mean score is higher than 65. He samples ten statistics students and obtains the scores 65 65 70 67 66 63 63 68 72 71. He performs a hypothesis test using a 5% level of significance. The data are assumed to be from a normal distribution.

Set up the hypothesis test:

A 5% level of significance means that \(\alpha = 0.05\). This is a test of a single population mean .

\(H_{0}: \mu = 65  H_{a}: \mu > 65\)

Since the instructor thinks the average score is higher, use a "\(>\)". The "\(>\)" means the test is right-tailed.

Determine the distribution needed:

Random variable: \(\bar{X} =\) average score on the first statistics test.

Distribution for the test: If you read the problem carefully, you will notice that there is no population standard deviation given . You are only given \(n = 10\) sample data values. Notice also that the data come from a normal distribution. This means that the distribution for the test is a student's \(t\).

Use \(t_{df}\). Therefore, the distribution for the test is \(t_{9}\) where \(n = 10\) and \(df = 10 - 1 = 9\).

The sample mean and sample standard deviation are calculated as 67 and 3.1972 from the data.

Calculate the \(p\)-value using the Student's \(t\)-distribution:

\[t_{obs} = \dfrac{\bar{x}-\mu_{\bar{x}}}{\left(\dfrac{s}{\sqrt{n}}\right)}=\dfrac{67-65}{\left(\dfrac{3.1972}{\sqrt{10}}\right)}\]

Use the T-table or Excel's t_dist() function to find p-value:

\(p\text{-value} = P(\bar{x} > 67) =P(T >1.9782 )= 1-0.9604=0.0396\)

Interpretation of the p -value: If the null hypothesis is true, then there is a 0.0396 probability (3.96%) that the sample mean is 65 or more.

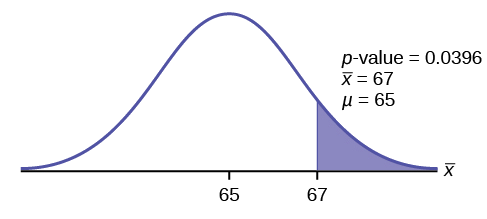
Compare \(\alpha\) and the \(p-\text{value}\):

Since \(α = 0.05\) and \(p\text{-value} = 0.0396\). \(\alpha > p\text{-value}\).

Make a decision: Since \(\alpha > p\text{-value}\), reject \(H_{0}\).

This means you reject \(\mu = 65\). In other words, you believe the average test score is more than 65.

Conclusion: At a 5% level of significance, the sample data show sufficient evidence that the mean (average) test score is more than 65, just as the math instructor thinks.

The \(p\text{-value}\) can easily be calculated.

Put the data into a list. Press STAT and arrow over to TESTS . Press 2:T-Test . Arrow over to Data and press ENTER . Arrow down and enter 65 for \(\mu_{0}\), the name of the list where you put the data, and 1 for Freq: . Arrow down to \(\mu\): and arrow over to \(> \mu_{0}\). Press ENTER . Arrow down to Calculate and press ENTER . The calculator not only calculates the \(p\text{-value}\) (p = 0.0396) but it also calculates the test statistic ( t -score) for the sample mean, the sample mean, and the sample standard deviation. \(\mu > 65\) is the alternative hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate ). Press ENTER . A shaded graph appears with \(t = 1.9781\) (test statistic) and \(p = 0.0396\) (\(p\text{-value}\)). Make sure when you use Draw that no other equations are highlighted in \(Y =\) and the plots are turned off.

Exercise \(\PageIndex{4}\)

It is believed that a stock price for a particular company will grow at a rate of $5 per week with a standard deviation of $1. An investor believes the stock won’t grow as quickly. The changes in stock price is recorded for ten weeks and are as follows: $4, $3, $2, $3, $1, $7, $2, $1, $1, $2. Perform a hypothesis test using a 5% level of significance. State the null and alternative hypotheses, find the p -value, state your conclusion, and identify the Type I and Type II errors.

• \(H_{0}: \mu = 5\)
• \(H_{a}: \mu < 5\)
• \(p = 0.0082\)

Because \(p < \alpha\), we reject the null hypothesis. There is sufficient evidence to suggest that the stock price of the company grows at a rate less than $5 a week.

• Type I Error: To conclude that the stock price is growing slower than $5 a week when, in fact, the stock price is growing at $5 a week (reject the null hypothesis when the null hypothesis is true).
• Type II Error: To conclude that the stock price is growing at a rate of $5 a week when, in fact, the stock price is growing slower than $5 a week (do not reject the null hypothesis when the null hypothesis is false).

Example \(\PageIndex{5}\)

The National Institute of Standards and Technology provides exact data on conductivity properties of materials. Following are conductivity measurements for 11 randomly selected pieces of a particular type of glass.

1.11; 1.07; 1.11; 1.07; 1.12; 1.08; .98; .98 1.02; .95; .95

Is there convincing evidence that the average conductivity of this type of glass is greater than one? Use a significance level of 0.05. Assume the population is normal.

Let’s follow a four-step process to answer this statistical question.

• \(H_{0}: \mu \leq 1\)
• \(H_{a}: \mu > 1\)
• Plan : We are testing a sample mean without a known population standard deviation. Therefore, we need to use a Student's-t distribution. Assume the underlying population is normal.
• Do the calculations : \(p\text{-value} ( = 0.036)\)

4. State the Conclusions : Since the \(p\text{-value} (= 0.036)\) is less than our alpha value, we will reject the null hypothesis. It is reasonable to state that the data supports the claim that the average conductivity level is greater than one.

The hypothesis test itself has an established process. This can be summarized as follows:

• Determine \(H_{0}\) and \(H_{a}\). Remember, they are contradictory.
• Determine the random variable.
• Determine the distribution for the test.
• Draw a graph, calculate the test statistic, and use the test statistic to calculate the \(p\text{-value}\). (A t -score is an example of test statistics.)
• Compare the preconceived α with the p -value, make a decision (reject or do not reject H 0 ), and write a clear conclusion using English sentences.

Notice that in performing the hypothesis test, you use \(\alpha\) and not \(\beta\). \(\beta\) is needed to help determine the sample size of the data that is used in calculating the \(p\text{-value}\). Remember that the quantity \(1 – \beta\) is called the Power of the Test . A high power is desirable. If the power is too low, statisticians typically increase the sample size while keeping α the same.If the power is low, the null hypothesis might not be rejected when it should be.

• Data from Amit Schitai. Director of Instructional Technology and Distance Learning. LBCC.
• Data from Bloomberg Businessweek . Available online at www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
• Data from energy.gov. Available online at http://energy.gov (accessed June 27. 2013).
• Data from Gallup®. Available online at www.gallup.com (accessed June 27, 2013).
• Data from Growing by Degrees by Allen and Seaman.
• Data from La Leche League International. Available online at www.lalecheleague.org/Law/BAFeb01.html.
• Data from the American Automobile Association. Available online at www.aaa.com (accessed June 27, 2013).
• Data from the American Library Association. Available online at www.ala.org (accessed June 27, 2013).
• Data from the Bureau of Labor Statistics. Available online at http://www.bls.gov/oes/current/oes291111.htm .
• Data from the Centers for Disease Control and Prevention. Available online at www.cdc.gov (accessed June 27, 2013)
• Data from the U.S. Census Bureau, available online at quickfacts.census.gov/qfd/states/00000.html (accessed June 27, 2013).
• Data from the United States Census Bureau. Available online at www.census.gov/hhes/socdemo/language/.
• Data from Toastmasters International. Available online at http://toastmasters.org/artisan/deta...eID=429&Page=1 .
• Data from Weather Underground. Available online at www.wunderground.com (accessed June 27, 2013).
• Federal Bureau of Investigations. “Uniform Crime Reports and Index of Crime in Daviess in the State of Kentucky enforced by Daviess County from 1985 to 2005.” Available online at http://www.disastercenter.com/kentucky/crime/3868.htm (accessed June 27, 2013).
• “Foothill-De Anza Community College District.” De Anza College, Winter 2006. Available online at research.fhda.edu/factbook/DA...t_da_2006w.pdf.
• Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Cellular Telephones and Cancer—a Nationwide Cohort Study in Denmark.” Institute of Cancer Epidemiology and the Danish Cancer Society, 93(3):203-7. Available online at http://www.ncbi.nlm.nih.gov/pubmed/11158188 (accessed June 27, 2013).
• Rape, Abuse & Incest National Network. “How often does sexual assault occur?” RAINN, 2009. Available online at www.rainn.org/get-information...sexual-assault (accessed June 27, 2013).

P-Value And Statistical Significance: What It Is & Why It Matters

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

The p-value in statistics quantifies the evidence against a null hypothesis. A low p-value suggests data is inconsistent with the null, potentially favoring an alternative hypothesis. Common significance thresholds are 0.05 or 0.01.

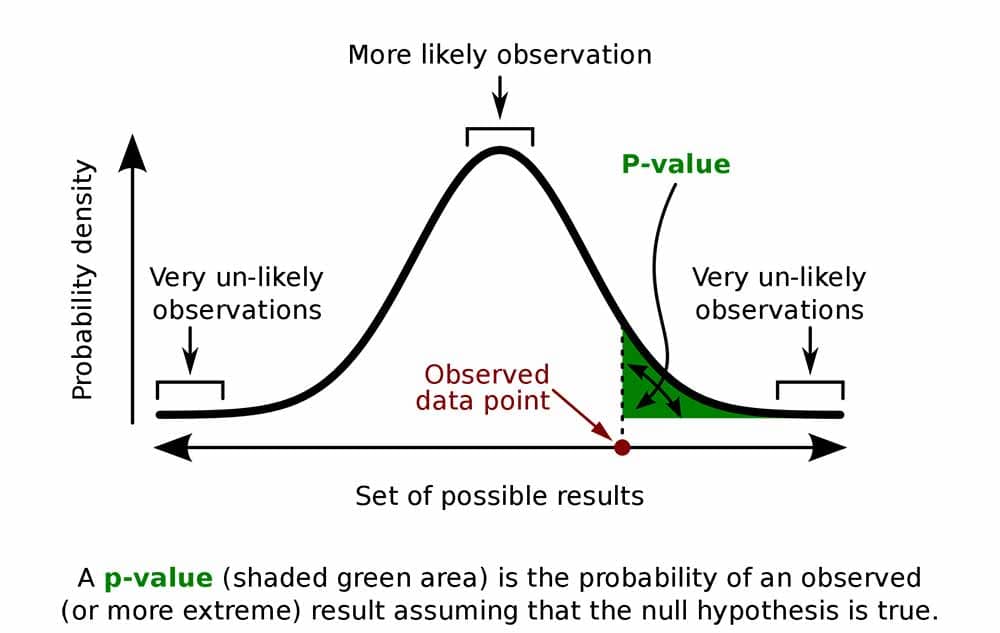
Hypothesis testing

When you perform a statistical test, a p-value helps you determine the significance of your results in relation to the null hypothesis.

The null hypothesis (H0) states no relationship exists between the two variables being studied (one variable does not affect the other). It states the results are due to chance and are not significant in supporting the idea being investigated. Thus, the null hypothesis assumes that whatever you try to prove did not happen.

The alternative hypothesis (Ha or H1) is the one you would believe if the null hypothesis is concluded to be untrue.

The alternative hypothesis states that the independent variable affected the dependent variable, and the results are significant in supporting the theory being investigated (i.e., the results are not due to random chance).

What a p-value tells you

A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true).

The level of statistical significance is often expressed as a p-value between 0 and 1.

The smaller the p -value, the less likely the results occurred by random chance, and the stronger the evidence that you should reject the null hypothesis.

Remember, a p-value doesn’t tell you if the null hypothesis is true or false. It just tells you how likely you’d see the data you observed (or more extreme data) if the null hypothesis was true. It’s a piece of evidence, not a definitive proof.

Example: Test Statistic and p-Value

Suppose you’re conducting a study to determine whether a new drug has an effect on pain relief compared to a placebo. If the new drug has no impact, your test statistic will be close to the one predicted by the null hypothesis (no difference between the drug and placebo groups), and the resulting p-value will be close to 1. It may not be precisely 1 because real-world variations may exist. Conversely, if the new drug indeed reduces pain significantly, your test statistic will diverge further from what’s expected under the null hypothesis, and the p-value will decrease. The p-value will never reach zero because there’s always a slim possibility, though highly improbable, that the observed results occurred by random chance.

P-value interpretation

The significance level (alpha) is a set probability threshold (often 0.05), while the p-value is the probability you calculate based on your study or analysis.

A p-value less than or equal to your significance level (typically ≤ 0.05) is statistically significant.

A p-value less than or equal to a predetermined significance level (often 0.05 or 0.01) indicates a statistically significant result, meaning the observed data provide strong evidence against the null hypothesis.

This suggests the effect under study likely represents a real relationship rather than just random chance.

For instance, if you set α = 0.05, you would reject the null hypothesis if your p -value ≤ 0.05. 

It indicates strong evidence against the null hypothesis, as there is less than a 5% probability the null is correct (and the results are random).

Therefore, we reject the null hypothesis and accept the alternative hypothesis.

Example: Statistical Significance

Upon analyzing the pain relief effects of the new drug compared to the placebo, the computed p-value is less than 0.01, which falls well below the predetermined alpha value of 0.05. Consequently, you conclude that there is a statistically significant difference in pain relief between the new drug and the placebo.

What does a p-value of 0.001 mean?

A p-value of 0.001 is highly statistically significant beyond the commonly used 0.05 threshold. It indicates strong evidence of a real effect or difference, rather than just random variation.

Specifically, a p-value of 0.001 means there is only a 0.1% chance of obtaining a result at least as extreme as the one observed, assuming the null hypothesis is correct.

Such a small p-value provides strong evidence against the null hypothesis, leading to rejecting the null in favor of the alternative hypothesis.

A p-value more than the significance level (typically p > 0.05) is not statistically significant and indicates strong evidence for the null hypothesis.

This means we retain the null hypothesis and reject the alternative hypothesis. You should note that you cannot accept the null hypothesis; we can only reject it or fail to reject it.

Note : when the p-value is above your threshold of significance,  it does not mean that there is a 95% probability that the alternative hypothesis is true.

One-Tailed Test

Two-Tailed Test

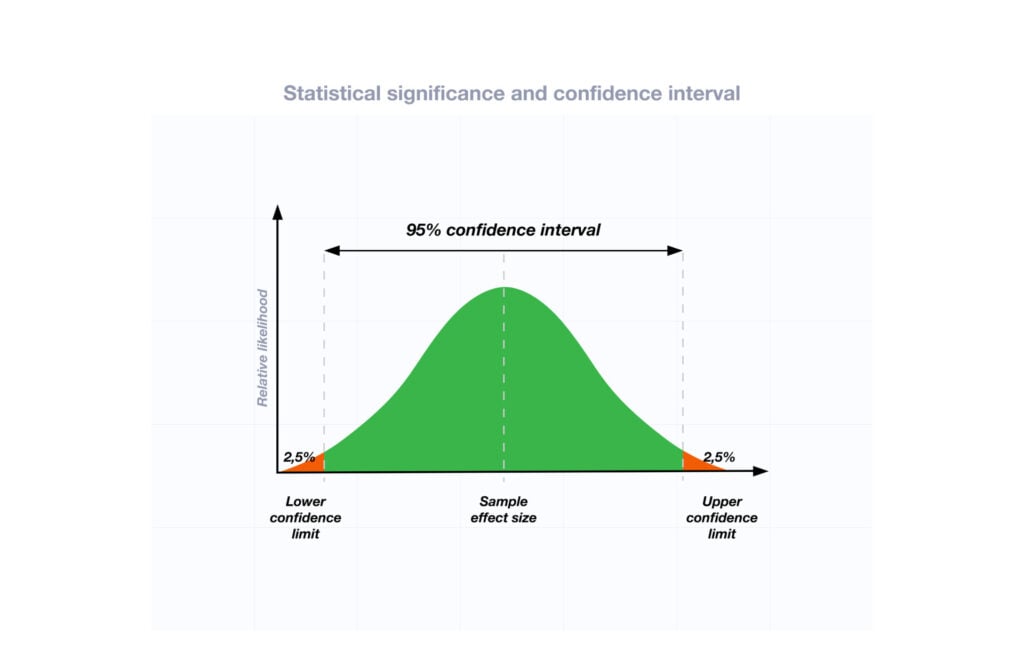
How do you calculate the p-value ?

Most statistical software packages like R, SPSS, and others automatically calculate your p-value. This is the easiest and most common way.

Online resources and tables are available to estimate the p-value based on your test statistic and degrees of freedom.

These tables help you understand how often you would expect to see your test statistic under the null hypothesis.

Understanding the Statistical Test:

Different statistical tests are designed to answer specific research questions or hypotheses. Each test has its own underlying assumptions and characteristics.

For example, you might use a t-test to compare means, a chi-squared test for categorical data, or a correlation test to measure the strength of a relationship between variables.

Be aware that the number of independent variables you include in your analysis can influence the magnitude of the test statistic needed to produce the same p-value.

This factor is particularly important to consider when comparing results across different analyses.

Example: Choosing a Statistical Test

If you’re comparing the effectiveness of just two different drugs in pain relief, a two-sample t-test is a suitable choice for comparing these two groups. However, when you’re examining the impact of three or more drugs, it’s more appropriate to employ an Analysis of Variance ( ANOVA) . Utilizing multiple pairwise comparisons in such cases can lead to artificially low p-values and an overestimation of the significance of differences between the drug groups.

How to report

A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty).

Instead, we may state our results “provide support for” or “give evidence for” our research hypothesis (as there is still a slight probability that the results occurred by chance and the null hypothesis was correct – e.g., less than 5%).

Example: Reporting the results

In our comparison of the pain relief effects of the new drug and the placebo, we observed that participants in the drug group experienced a significant reduction in pain ( M = 3.5; SD = 0.8) compared to those in the placebo group ( M = 5.2; SD  = 0.7), resulting in an average difference of 1.7 points on the pain scale (t(98) = -9.36; p < 0.001).

The 6th edition of the APA style manual (American Psychological Association, 2010) states the following on the topic of reporting p-values:

“When reporting p values, report exact p values (e.g., p = .031) to two or three decimal places. However, report p values less than .001 as p < .001.

The tradition of reporting p values in the form p < .10, p < .05, p < .01, and so forth, was appropriate in a time when only limited tables of critical values were available.” (p. 114)

• Do not use 0 before the decimal point for the statistical value p as it cannot equal 1. In other words, write p = .001 instead of p = 0.001.
• Please pay attention to issues of italics ( p is always italicized) and spacing (either side of the = sign).
• p = .000 (as outputted by some statistical packages such as SPSS) is impossible and should be written as p < .001.
• The opposite of significant is “nonsignificant,” not “insignificant.”

Why is the p -value not enough?

A lower p-value  is sometimes interpreted as meaning there is a stronger relationship between two variables.

However, statistical significance means that it is unlikely that the null hypothesis is true (less than 5%).

To understand the strength of the difference between the two groups (control vs. experimental) a researcher needs to calculate the effect size .

When do you reject the null hypothesis?

In statistical hypothesis testing, you reject the null hypothesis when the p-value is less than or equal to the significance level (α) you set before conducting your test. The significance level is the probability of rejecting the null hypothesis when it is true. Commonly used significance levels are 0.01, 0.05, and 0.10.

Remember, rejecting the null hypothesis doesn’t prove the alternative hypothesis; it just suggests that the alternative hypothesis may be plausible given the observed data.

The p -value is conditional upon the null hypothesis being true but is unrelated to the truth or falsity of the alternative hypothesis.

What does p-value of 0.05 mean?

If your p-value is less than or equal to 0.05 (the significance level), you would conclude that your result is statistically significant. This means the evidence is strong enough to reject the null hypothesis in favor of the alternative hypothesis.

Are all p-values below 0.05 considered statistically significant?

No, not all p-values below 0.05 are considered statistically significant. The threshold of 0.05 is commonly used, but it’s just a convention. Statistical significance depends on factors like the study design, sample size, and the magnitude of the observed effect.

A p-value below 0.05 means there is evidence against the null hypothesis, suggesting a real effect. However, it’s essential to consider the context and other factors when interpreting results.

Researchers also look at effect size and confidence intervals to determine the practical significance and reliability of findings.

How does sample size affect the interpretation of p-values?

Sample size can impact the interpretation of p-values. A larger sample size provides more reliable and precise estimates of the population, leading to narrower confidence intervals.

With a larger sample, even small differences between groups or effects can become statistically significant, yielding lower p-values. In contrast, smaller sample sizes may not have enough statistical power to detect smaller effects, resulting in higher p-values.

Therefore, a larger sample size increases the chances of finding statistically significant results when there is a genuine effect, making the findings more trustworthy and robust.

Can a non-significant p-value indicate that there is no effect or difference in the data?

No, a non-significant p-value does not necessarily indicate that there is no effect or difference in the data. It means that the observed data do not provide strong enough evidence to reject the null hypothesis.

There could still be a real effect or difference, but it might be smaller or more variable than the study was able to detect.

Other factors like sample size, study design, and measurement precision can influence the p-value. It’s important to consider the entire body of evidence and not rely solely on p-values when interpreting research findings.

Can P values be exactly zero?

While a p-value can be extremely small, it cannot technically be absolute zero. When a p-value is reported as p = 0.000, the actual p-value is too small for the software to display. This is often interpreted as strong evidence against the null hypothesis. For p values less than 0.001, report as p < .001

Further Information

• P-values and significance tests (Kahn Academy)
• Hypothesis testing and p-values (Kahn Academy)
• Wasserstein, R. L., Schirm, A. L., & Lazar, N. A. (2019). Moving to a world beyond “ p “< 0.05”.
• Criticism of using the “ p “< 0.05”.
• Publication manual of the American Psychological Association
• Statistics for Psychology Book Download

Bland, J. M., & Altman, D. G. (1994). One and two sided tests of significance: Authors’ reply.  BMJ: British Medical Journal ,  309 (6958), 874.

Goodman, S. N., & Royall, R. (1988). Evidence and scientific research.  American Journal of Public Health ,  78 (12), 1568-1574.

Goodman, S. (2008, July). A dirty dozen: twelve p-value misconceptions . In  Seminars in hematology  (Vol. 45, No. 3, pp. 135-140). WB Saunders.

Lang, J. M., Rothman, K. J., & Cann, C. I. (1998). That confounded P-value.  Epidemiology (Cambridge, Mass.) ,  9 (1), 7-8.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3.2 hypothesis testing (p-value approach).

The P -value approach involves determining "likely" or "unlikely" by determining the probability — assuming the null hypothesis was true — of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed. If the P -value is small, say less than (or equal to) \(\alpha\), then it is "unlikely." And, if the P -value is large, say more than \(\alpha\), then it is "likely."

If the P -value is less than (or equal to) \(\alpha\), then the null hypothesis is rejected in favor of the alternative hypothesis. And, if the P -value is greater than \(\alpha\), then the null hypothesis is not rejected.

Specifically, the four steps involved in using the P -value approach to conducting any hypothesis test are:

• Specify the null and alternative hypotheses.
• Using the sample data and assuming the null hypothesis is true, calculate the value of the test statistic. Again, to conduct the hypothesis test for the population mean μ , we use the t -statistic \(t^*=\frac{\bar{x}-\mu}{s/\sqrt{n}}\) which follows a t -distribution with n - 1 degrees of freedom.
• Using the known distribution of the test statistic, calculate the P -value : "If the null hypothesis is true, what is the probability that we'd observe a more extreme test statistic in the direction of the alternative hypothesis than we did?" (Note how this question is equivalent to the question answered in criminal trials: "If the defendant is innocent, what is the chance that we'd observe such extreme criminal evidence?")
• Set the significance level, \(\alpha\), the probability of making a Type I error to be small — 0.01, 0.05, or 0.10. Compare the P -value to \(\alpha\). If the P -value is less than (or equal to) \(\alpha\), reject the null hypothesis in favor of the alternative hypothesis. If the P -value is greater than \(\alpha\), do not reject the null hypothesis.

Example S.3.2.1

Mean gpa section  .

In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t * equaling 2.5. Since n = 15, our test statistic t * has n - 1 = 14 degrees of freedom. Also, suppose we set our significance level α at 0.05 so that we have only a 5% chance of making a Type I error.

Right Tailed

The P -value for conducting the right-tailed test H 0 : μ = 3 versus H A : μ > 3 is the probability that we would observe a test statistic greater than t * = 2.5 if the population mean \(\mu\) really were 3. Recall that probability equals the area under the probability curve. The P -value is therefore the area under a t n - 1 = t 14 curve and to the right of the test statistic t * = 2.5. It can be shown using statistical software that the P -value is 0.0127. The graph depicts this visually.

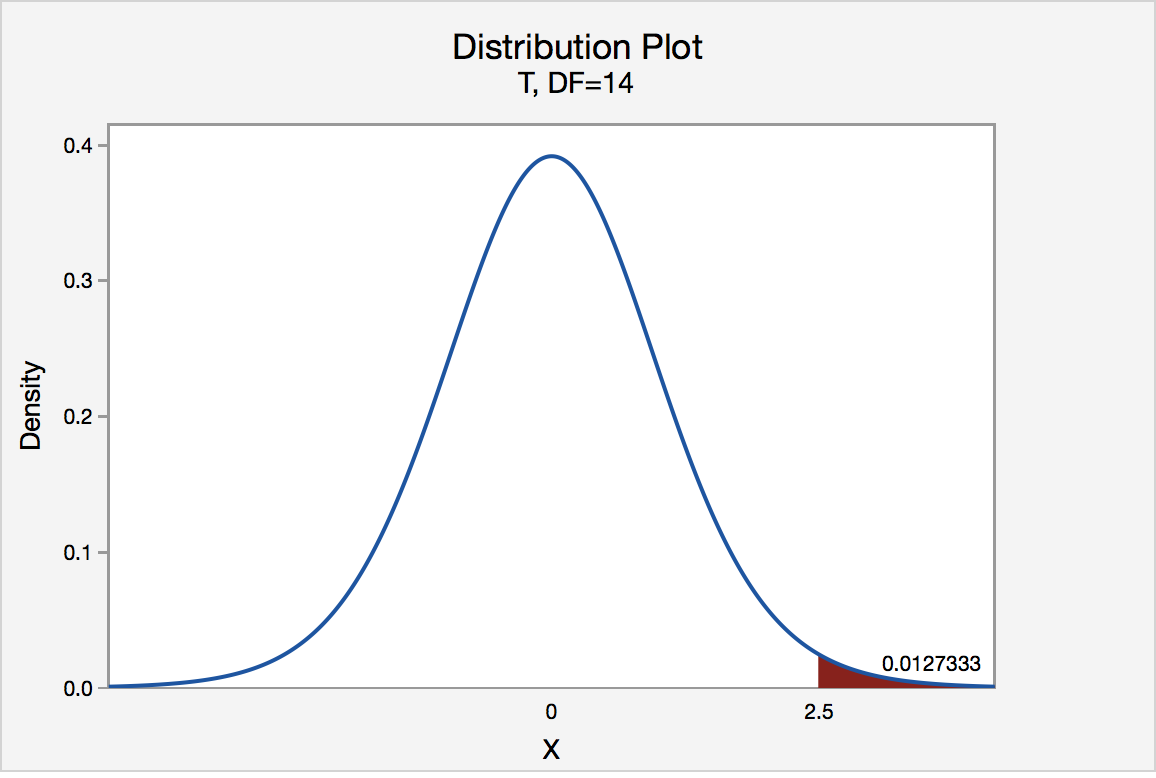
The P -value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0127, is less than \(\alpha\) = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ > 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ > 3 if we lowered our willingness to make a Type I error to \(\alpha\) = 0.01 instead, as the P -value, 0.0127, is then greater than \(\alpha\) = 0.01.

Left Tailed

In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t * instead of equaling -2.5. The P -value for conducting the left-tailed test H 0 : μ = 3 versus H A : μ < 3 is the probability that we would observe a test statistic less than t * = -2.5 if the population mean μ really were 3. The P -value is therefore the area under a t n - 1 = t 14 curve and to the left of the test statistic t* = -2.5. It can be shown using statistical software that the P -value is 0.0127. The graph depicts this visually.

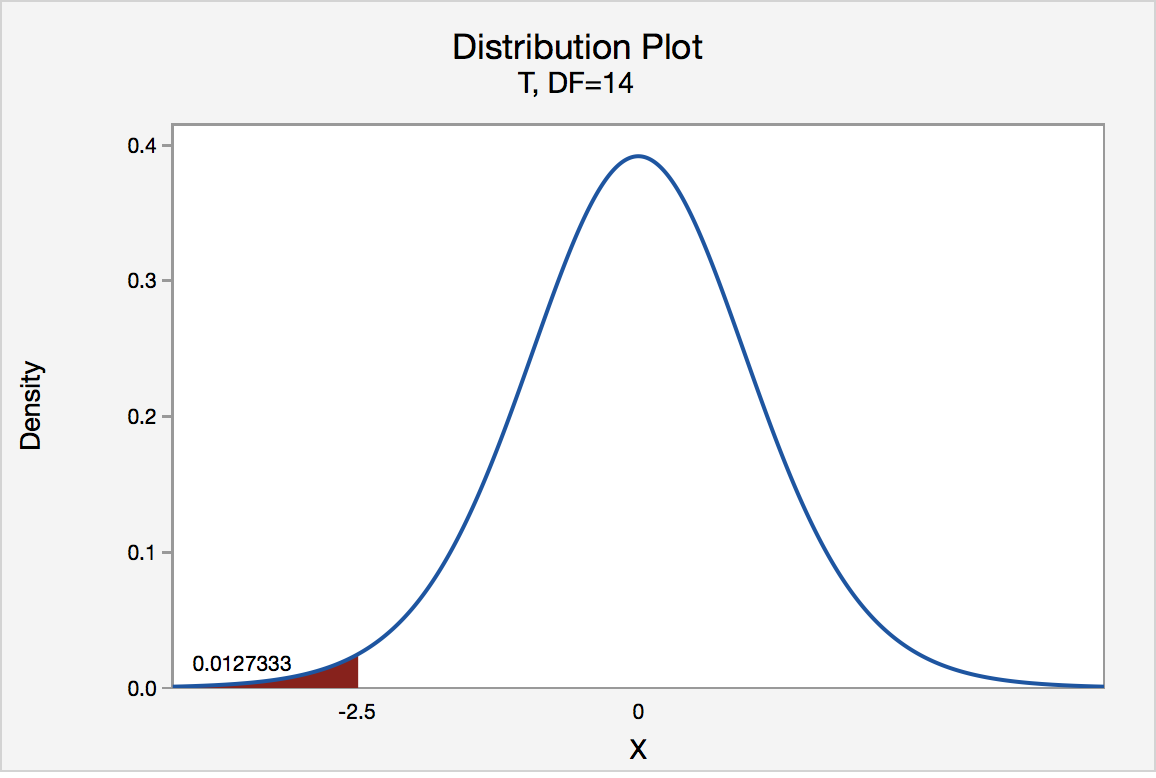
The P -value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0127, is less than α = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ < 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ < 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P -value, 0.0127, is then greater than \(\alpha\) = 0.01.

In our example concerning the mean grade point average, suppose again that our random sample of n = 15 students majoring in mathematics yields a test statistic t * instead of equaling -2.5. The P -value for conducting the two-tailed test H 0 : μ = 3 versus H A : μ ≠ 3 is the probability that we would observe a test statistic less than -2.5 or greater than 2.5 if the population mean μ really was 3. That is, the two-tailed test requires taking into account the possibility that the test statistic could fall into either tail (hence the name "two-tailed" test). The P -value is, therefore, the area under a t n - 1 = t 14 curve to the left of -2.5 and to the right of 2.5. It can be shown using statistical software that the P -value is 0.0127 + 0.0127, or 0.0254. The graph depicts this visually.

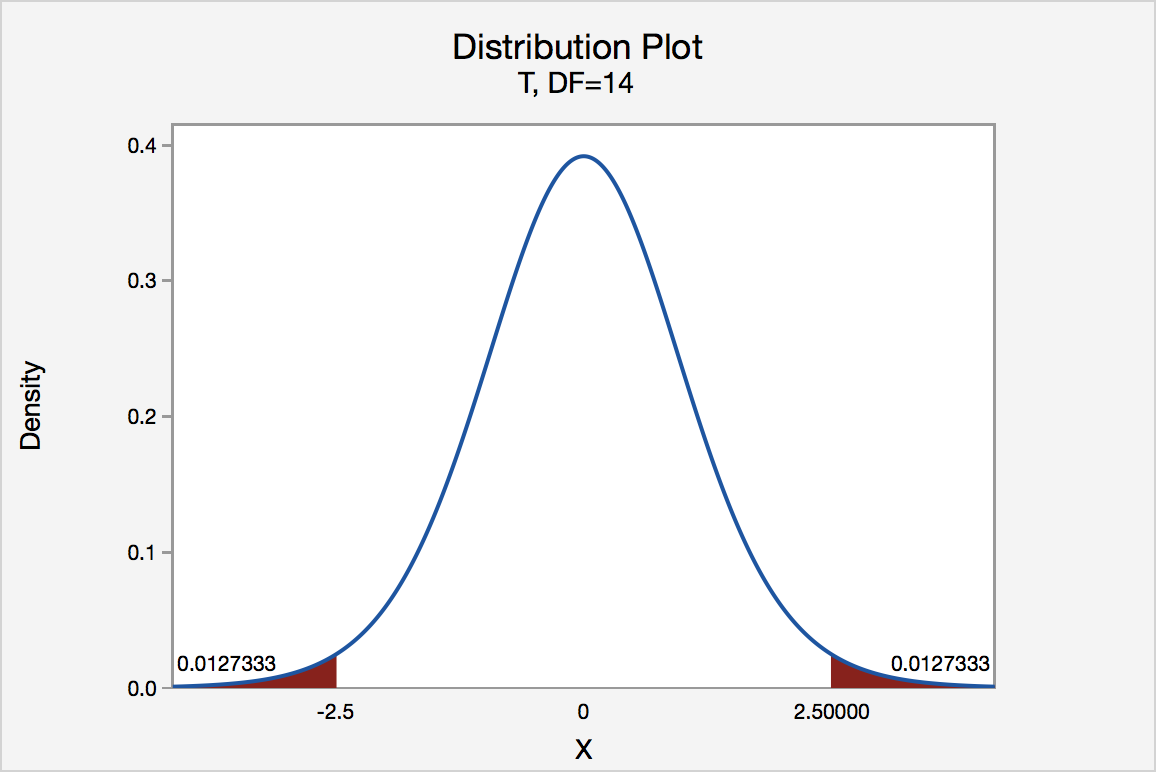
Note that the P -value for a two-tailed test is always two times the P -value for either of the one-tailed tests. The P -value, 0.0254, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0254, is less than α = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ ≠ 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ ≠ 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P -value, 0.0254, is then greater than \(\alpha\) = 0.01.

Now that we have reviewed the critical value and P -value approach procedures for each of the three possible hypotheses, let's look at three new examples — one of a right-tailed test, one of a left-tailed test, and one of a two-tailed test.

The good news is that, whenever possible, we will take advantage of the test statistics and P -values reported in statistical software, such as Minitab, to conduct our hypothesis tests in this course.