null and alternative hypothesis for linear regression

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

13.6 Testing the Regression Coefficients

Learning objectives.

Conduct and interpret a hypothesis test on individual regression coefficients.

Previously, we learned that the population model for the multiple regression equation is

[latex]\begin{eqnarray*} y & = & \beta_0+\beta_1x_1+\beta_2x_2+\cdots+\beta_kx_k +\epsilon \end{eqnarray*}[/latex]

where [latex]x_1,x_2,\ldots,x_k[/latex] are the independent variables, [latex]\beta_0,\beta_1,\ldots,\beta_k[/latex] are the population parameters of the regression coefficients, and [latex]\epsilon[/latex] is the error variable. In multiple regression, we estimate each population regression coefficient [latex]\beta_i[/latex] with the sample regression coefficient [latex]b_i[/latex].

In the previous section, we learned how to conduct an overall model test to determine if the regression model is valid. If the outcome of the overall model test is that the model is valid, then at least one of the independent variables is related to the dependent variable—in other words, at least one of the regression coefficients [latex]\beta_i[/latex] is not zero. However, the overall model test does not tell us which independent variables are related to the dependent variable. To determine which independent variables are related to the dependent variable, we must test each of the regression coefficients.

Testing the Regression Coefficients

For an individual regression coefficient, we want to test if there is a relationship between the dependent variable [latex]y[/latex] and the independent variable [latex]x_i[/latex].

No Relationship . There is no relationship between the dependent variable [latex]y[/latex] and the independent variable [latex]x_i[/latex]. In this case, the regression coefficient [latex]\beta_i[/latex] is zero. This is the claim for the null hypothesis in an individual regression coefficient test: [latex]H_0: \beta_i=0[/latex].
Relationship. There is a relationship between the dependent variable [latex]y[/latex] and the independent variable [latex]x_i[/latex]. In this case, the regression coefficients [latex]\beta_i[/latex] is not zero. This is the claim for the alternative hypothesis in an individual regression coefficient test: [latex]H_a: \beta_i \neq 0[/latex]. We are not interested if the regression coefficient [latex]\beta_i[/latex] is positive or negative, only that it is not zero. We only need to find out if the regression coefficient is not zero to demonstrate that there is a relationship between the dependent variable and the independent variable. This makes the test on a regression coefficient a two-tailed test.

In order to conduct a hypothesis test on an individual regression coefficient [latex]\beta_i[/latex], we need to use the distribution of the sample regression coefficient [latex]b_i[/latex]:

The mean of the distribution of the sample regression coefficient is the population regression coefficient [latex]\beta_i[/latex].
The standard deviation of the distribution of the sample regression coefficient is [latex]\sigma_{b_i}[/latex]. Because we do not know the population standard deviation we must estimate [latex]\sigma_{b_i}[/latex] with the sample standard deviation [latex]s_{b_i}[/latex].
The distribution of the sample regression coefficient follows a normal distribution.

Steps to Conduct a Hypothesis Test on a Regression Coefficient

[latex]\begin{eqnarray*} H_0: & & \beta_i=0 \\ \\ \end{eqnarray*}[/latex]

[latex]\begin{eqnarray*} H_a: & & \beta_i \neq 0 \\ \\ \end{eqnarray*}[/latex]

Collect the sample information for the test and identify the significance level [latex]\alpha[/latex].

[latex]\begin{eqnarray*}t & = & \frac{b_i-\beta_i}{s_{b_i}} \\ \\ df & = & n-k-1 \\ \\ \end{eqnarray*}[/latex]

The results of the sample data are significant. There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
Write down a concluding sentence specific to the context of the question.

The required [latex]t[/latex]-score and p -value for the test can be found on the regression summary table, which we learned how to generate in Excel in a previous section.

The human resources department at a large company wants to develop a model to predict an employee’s job satisfaction from the number of hours of unpaid work per week the employee does, the employee’s age, and the employee’s income. A sample of 25 employees at the company is taken and the data is recorded in the table below. The employee’s income is recorded in $1000s and the job satisfaction score is out of 10, with higher values indicating greater job satisfaction.

Previously, we found the multiple regression equation to predict the job satisfaction score from the other variables:

[latex]\begin{eqnarray*} \hat{y} & = & 4.7993-0.3818x_1+0.0046x_2+0.0233x_3 \\ \\ \hat{y} & = & \mbox{predicted job satisfaction score} \\ x_1 & = & \mbox{hours of unpaid work per week} \\ x_2 & = & \mbox{age} \\ x_3 & = & \mbox{income (\$1000s)}\end{eqnarray*}[/latex]

At the 5% significance level, test the relationship between the dependent variable “job satisfaction” and the independent variable “hours of unpaid work per week”.

Hypotheses:

[latex]\begin{eqnarray*} H_0: & & \beta_1=0 \\ H_a: & & \beta_1 \neq 0 \end{eqnarray*}[/latex]

The regression summary table generated by Excel is shown below:

The p -value for the test on the hours of unpaid work per week regression coefficient is in the bottom part of the table under the P-value column of the Hours of Unpaid Work per Week row . So the p -value=[latex]0.0082[/latex].

Conclusion:

Because p -value[latex]=0.0082 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 5% significance level there is enough evidence to suggest that there is a relationship between the dependent variable “job satisfaction” and the independent variable “hours of unpaid work per week.”

The null hypothesis [latex]\beta_1=0[/latex] is the claim that the regression coefficient for the independent variable [latex]x_1[/latex] is zero. That is, the null hypothesis is the claim that there is no relationship between the dependent variable and the independent variable “hours of unpaid work per week.”
The alternative hypothesis is the claim that the regression coefficient for the independent variable [latex]x_1[/latex] is not zero. The alternative hypothesis is the claim that there is a relationship between the dependent variable and the independent variable “hours of unpaid work per week.”
When conducting a test on a regression coefficient, make sure to use the correct subscript on [latex]\beta[/latex] to correspond to how the independent variables were defined in the regression model and which independent variable is being tested. Here the subscript on [latex]\beta[/latex] is 1 because the “hours of unpaid work per week” is defined as [latex]x_1[/latex] in the regression model.
The p -value for the tests on the regression coefficients are located in the bottom part of the table under the P-value column heading in the corresponding independent variable row.
Because the alternative hypothesis is a [latex]\neq[/latex], the p -value is the sum of the area in the tails of the [latex]t[/latex]-distribution. This is the value calculated out by Excel in the regression summary table.
The p -value of 0.0082 is a small probability compared to the significance level, and so is unlikely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the regression coefficient [latex]\beta_1[/latex] is not zero, and so there is a relationship between the dependent variable “job satisfaction” and the independent variable “hours of unpaid work per week.” This means that the independent variable “hours of unpaid work per week” is useful in predicting the dependent variable.

At the 5% significance level, test the relationship between the dependent variable “job satisfaction” and the independent variable “age”.

[latex]\begin{eqnarray*} H_0: & & \beta_2=0 \\ H_a: & & \beta_2 \neq 0 \end{eqnarray*}[/latex]

The p -value for the test on the age regression coefficient is in the bottom part of the table under the P-value column of the Age row . So the p -value=[latex]0.8439[/latex].

Because p -value[latex]=0.8439 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis. At the 5% significance level there is not enough evidence to suggest that there is a relationship between the dependent variable “job satisfaction” and the independent variable “age.”

The null hypothesis [latex]\beta_2=0[/latex] is the claim that the regression coefficient for the independent variable [latex]x_2[/latex] is zero. That is, the null hypothesis is the claim that there is no relationship between the dependent variable and the independent variable “age.”
The alternative hypothesis is the claim that the regression coefficient for the independent variable [latex]x_2[/latex] is not zero. The alternative hypothesis is the claim that there is a relationship between the dependent variable and the independent variable “age.”
When conducting a test on a regression coefficient, make sure to use the correct subscript on [latex]\beta[/latex] to correspond to how the independent variables were defined in the regression model and which independent variable is being tested. Here the subscript on [latex]\beta[/latex] is 2 because “age” is defined as [latex]x_2[/latex] in the regression model.
The p -value of 0.8439 is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the regression coefficient [latex]\beta_2[/latex] is zero, and so there is no relationship between the dependent variable “job satisfaction” and the independent variable “age.” This means that the independent variable “age” is not particularly useful in predicting the dependent variable.

At the 5% significance level, test the relationship between the dependent variable “job satisfaction” and the independent variable “income”.

[latex]\begin{eqnarray*} H_0: & & \beta_3=0 \\ H_a: & & \beta_3 \neq 0 \end{eqnarray*}[/latex]

The p -value for the test on the income regression coefficient is in the bottom part of the table under the P-value column of the Income row . So the p -value=[latex]0.0060[/latex].

Because p -value[latex]=0.0060 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 5% significance level there is enough evidence to suggest that there is a relationship between the dependent variable “job satisfaction” and the independent variable “income.”

The null hypothesis [latex]\beta_3=0[/latex] is the claim that the regression coefficient for the independent variable [latex]x_3[/latex] is zero. That is, the null hypothesis is the claim that there is no relationship between the dependent variable and the independent variable “income.”
The alternative hypothesis is the claim that the regression coefficient for the independent variable [latex]x_3[/latex] is not zero. The alternative hypothesis is the claim that there is a relationship between the dependent variable and the independent variable “income.”
When conducting a test on a regression coefficient, make sure to use the correct subscript on [latex]\beta[/latex] to correspond to how the independent variables were defined in the regression model and which independent variable is being tested. Here the subscript on [latex]\beta[/latex] is 3 because “income” is defined as [latex]x_3[/latex] in the regression model.
The p -value of 0.0060 is a small probability compared to the significance level, and so is unlikely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the regression coefficient [latex]\beta_3[/latex] is not zero, and so there is a relationship between the dependent variable “job satisfaction” and the independent variable “income.” This means that the independent variable “income” is useful in predicting the dependent variable.

Concept Review

The test on a regression coefficient determines if there is a relationship between the dependent variable and the corresponding independent variable. The p -value for the test is the sum of the area in tails of the [latex]t[/latex]-distribution. The p -value can be found on the regression summary table generated by Excel.

The hypothesis test for a regression coefficient is a well established process:

Write down the null and alternative hypotheses in terms of the regression coefficient being tested. The null hypothesis is the claim that there is no relationship between the dependent variable and independent variable. The alternative hypothesis is the claim that there is a relationship between the dependent variable and independent variable.
Collect the sample information for the test and identify the significance level.
The p -value is the sum of the area in the tails of the [latex]t[/latex]-distribution. Use the regression summary table generated by Excel to find the p -value.
Compare the p -value to the significance level and state the outcome of the test.

Understanding the Null Hypothesis for Linear Regression

Linear regression is a technique we can use to understand the relationship between one or more predictor variables and a response variable .

If we only have one predictor variable and one response variable, we can use simple linear regression , which uses the following formula to estimate the relationship between the variables:

ŷ = β 0 + β 1 x

ŷ: The estimated response value.
β 0 : The average value of y when x is zero.
β 1 : The average change in y associated with a one unit increase in x.
x: The value of the predictor variable.

Simple linear regression uses the following null and alternative hypotheses:

H 0 : β 1 = 0
H A : β 1 ≠ 0

The null hypothesis states that the coefficient β 1 is equal to zero. In other words, there is no statistically significant relationship between the predictor variable, x, and the response variable, y.

The alternative hypothesis states that β 1 is not equal to zero. In other words, there is a statistically significant relationship between x and y.

If we have multiple predictor variables and one response variable, we can use multiple linear regression , which uses the following formula to estimate the relationship between the variables:

ŷ = β 0 + β 1 x 1 + β 2 x 2 + … + β k x k

β 0 : The average value of y when all predictor variables are equal to zero.
β i : The average change in y associated with a one unit increase in x i .
x i : The value of the predictor variable x i .

Multiple linear regression uses the following null and alternative hypotheses:

H 0 : β 1 = β 2 = … = β k = 0
H A : β 1 = β 2 = … = β k ≠ 0

The null hypothesis states that all coefficients in the model are equal to zero. In other words, none of the predictor variables have a statistically significant relationship with the response variable, y.

The alternative hypothesis states that not every coefficient is simultaneously equal to zero.

The following examples show how to decide to reject or fail to reject the null hypothesis in both simple linear regression and multiple linear regression models.

Example 1: Simple Linear Regression

Suppose a professor would like to use the number of hours studied to predict the exam score that students will receive in his class. He collects data for 20 students and fits a simple linear regression model.

The following screenshot shows the output of the regression model:

Output of simple linear regression in Excel

The fitted simple linear regression model is:

Exam Score = 67.1617 + 5.2503*(hours studied)

To determine if there is a statistically significant relationship between hours studied and exam score, we need to analyze the overall F value of the model and the corresponding p-value:

Overall F-Value: 47.9952
P-value: 0.000

Since this p-value is less than .05, we can reject the null hypothesis. In other words, there is a statistically significant relationship between hours studied and exam score received.

Example 2: Multiple Linear Regression

Suppose a professor would like to use the number of hours studied and the number of prep exams taken to predict the exam score that students will receive in his class. He collects data for 20 students and fits a multiple linear regression model.

Multiple linear regression output in Excel

The fitted multiple linear regression model is:

Exam Score = 67.67 + 5.56*(hours studied) – 0.60*(prep exams taken)

To determine if there is a jointly statistically significant relationship between the two predictor variables and the response variable, we need to analyze the overall F value of the model and the corresponding p-value:

Overall F-Value: 23.46
P-value: 0.00

Since this p-value is less than .05, we can reject the null hypothesis. In other words, hours studied and prep exams taken have a jointly statistically significant relationship with exam score.

Note: Although the p-value for prep exams taken (p = 0.52) is not significant, prep exams combined with hours studied has a significant relationship with exam score.

Additional Resources

Understanding the F-Test of Overall Significance in Regression How to Read and Interpret a Regression Table How to Report Regression Results How to Perform Simple Linear Regression in Excel How to Perform Multiple Linear Regression in Excel

The Complete Guide: How to Report Regression Results

R vs. r-squared: what’s the difference, related posts, how to normalize data between -1 and 1, how to interpret f-values in a two-way anova, how to create a vector of ones in..., vba: how to check if string contains another..., how to determine if a probability distribution is..., what is a symmetric histogram (definition & examples), how to find the mode of a histogram..., how to find quartiles in even and odd..., how to calculate sxy in statistics (with example), how to calculate sxx in statistics (with example).

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : μ __ 66
H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : μ __ 45
H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : p __ 0.40
H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

Authors: Barbara Illowsky, Susan Dean
Publisher/website: OpenStax
Book title: Statistics
Publication date: Mar 27, 2020
Location: Houston, Texas
Book URL: https://openstax.org/books/statistics/pages/1-introduction
Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Statistics Made Easy

How to Test the Significance of a Regression Slope

Suppose we have the following dataset that shows the square feet and price of 12 different houses:

We want to know if there is a significant relationship between square feet and price.

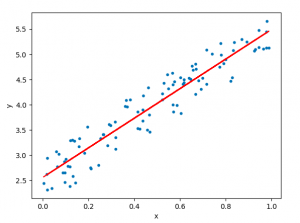
To get an idea of what the data looks like, we first create a scatterplot with square feet on the x-axis and price on the y-axis:

We can clearly see that there is a positive correlation between square feet and price. As square feet increases, the price of the house tends to increase as well.

However, to know if there is a statistically significant relationship between square feet and price, we need to run a simple linear regression.

So, we run a simple linear regression using square feet as the predictor and price as the response and get the following output:

Whether you run a simple linear regression in Excel, SPSS, R, or some other software, you will get a similar output to the one shown above.

Recall that a simple linear regression will produce the line of best fit, which is the equation for the line that best “fits” the data on our scatterplot. This line of best fit is defined as:

ŷ = b 0 + b 1 x

where ŷ is the predicted value of the response variable, b 0 is the y-intercept, b 1 is the regression coefficient, and x is the value of the predictor variable.

The value for b 0 is given by the coefficient for the intercept, which is 47588.70.

The value for b 1 is given by the coefficient for the predictor variable Square Feet , which is 93.57.

Thus, the line of best fit in this example is ŷ = 47588.70+ 93.57x

Here is how to interpret this line of best fit:

b 0 : When the value for square feet is zero, the average expected value for price is $47,588.70. (In this case, it doesn’t really make sense to interpret the intercept, since a house can never have zero square feet)
b 1 : For each additional square foot, the average expected increase in price is $93.57.

So, now we know that for each additional square foot, the average expected increase in price is $93.57.

To find out if this increase is statistically significant, we need to conduct a hypothesis test for B 1 or construct a confidence interval for B 1 .

Note : A hypothesis test and a confidence interval will always give the same results.

Constructing a Confidence Interval for a Regression Slope

To construct a confidence interval for a regression slope, we use the following formula:

Confidence Interval = b 1 +/- (t 1-∝/2, n-2 ) * (standard error of b 1 )

b 1 is the slope coefficient given in the regression output
(t 1-∝/2, n-2 ) is the t critical value for confidence level 1-∝ with n-2 degrees of freedom where n is the total number of observations in our dataset
(standard error of b 1 ) is the standard error of b 1 given in the regression output

For our example, here is how to construct a 95% confidence interval for B 1 :

b 1 is 93.57 from the regression output.
Since we are using a 95% confidence interval, ∝ = .05 and n-2 = 12-2 = 10, thus t .975, 10 is 2.228 according to the t-distribution table
(standard error of b 1 ) is 11.45 from the regression output

Thus, our 95% confidence interval for B 1 is:

93.57 +/- (2.228) * (11.45) = (68.06 , 119.08)

This means we are 95% confident that the true average increase in price for each additional square foot is between $68.06 and $119.08.

Notice that $0 is not in this interval, so the relationship between square feet and price is statistically significant at the 95% confidence level.

Conducting a Hypothesis Test for a Regression Slope

To conduct a hypothesis test for a regression slope, we follow the standard five steps for any hypothesis test :

Step 1. State the hypotheses.

The null hypothesis (H0): B 1 = 0

The alternative hypothesis: (Ha): B 1 ≠ 0

Step 2. Determine a significance level to use.

Since we constructed a 95% confidence interval in the previous example, we will use the equivalent approach here and choose to use a .05 level of significance.

Step 3. Find the test statistic and the corresponding p-value.

In this case, the test statistic is t = coefficient of b 1 / standard error of b 1 with n-2 degrees of freedom. We can find these values from the regression output:

Using the T Score to P Value Calculator with a t score of 6.69 with 10 degrees of freedom and a two-tailed test, the p-value = 0.000 .

Step 4. Reject or fail to reject the null hypothesis.

Since the p-value is less than our significance level of .05, we reject the null hypothesis.

Step 5. Interpret the results.

Since we rejected the null hypothesis, we have sufficient evidence to say that the true average increase in price for each additional square foot is not zero.

Featured Posts

5 Regularization Techniques You Should Know

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

4 Replies to “How to Test the Significance of a Regression Slope”

Thank you!:)

I am a bit confused!

The p-value is less than our alpha=0.05.

Shouldnt be the other way around that we fail to reject the H_0 hypothesis?

Why does this output change between the two examples you show? I don’t understand.

The coefficient of b1 in the first table is 93.57173

The coefficient of b1 in the second table is 92.89

Did something change or was this example not carried through the entire way through the section “Conducting a Hypothesis Test for a Regression Slope?” This is very confusing.

Hello Zach. Thank you for all of your articles on statology.org website. For the first time, I request your help about the Hypothesis Test for a Regression Slope above. I would like to know how the regression output in “Step 3. find the test statistic and the corresponding p-value” was obtained. Thank you. Elia

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

Prompt Library
DS/AI Trends
Stats Tools
Interview Questions
Generative AI
Machine Learning
Deep Learning

Linear regression hypothesis testing: Concepts, Examples

In relation to machine learning , linear regression is defined as a predictive modeling technique that allows us to build a model which can help predict continuous response variables as a function of a linear combination of explanatory or predictor variables. While training linear regression models, we need to rely on hypothesis testing in relation to determining the relationship between the response and predictor variables. In the case of the linear regression model, two types of hypothesis testing are done. They are T-tests and F-tests . In other words, there are two types of statistics that are used to assess whether linear regression models exist representing response and predictor variables. They are t-statistics and f-statistics. As data scientists , it is of utmost importance to determine if linear regression is the correct choice of model for our particular problem and this can be done by performing hypothesis testing related to linear regression response and predictor variables. Many times, it is found that these concepts are not very clear with a lot many data scientists. In this blog post, we will discuss linear regression and hypothesis testing related to t-statistics and f-statistics . We will also provide an example to help illustrate how these concepts work.

Table of Contents

What are linear regression models?

A linear regression model can be defined as the function approximation that represents a continuous response variable as a function of one or more predictor variables. While building a linear regression model, the goal is to identify a linear equation that best predicts or models the relationship between the response or dependent variable and one or more predictor or independent variables.

There are two different kinds of linear regression models. They are as follows:

Simple or Univariate linear regression models : These are linear regression models that are used to build a linear relationship between one response or dependent variable and one predictor or independent variable. The form of the equation that represents a simple linear regression model is Y=mX+b, where m is the coefficients of the predictor variable and b is bias. When considering the linear regression line, m represents the slope and b represents the intercept.
Multiple or Multi-variate linear regression models : These are linear regression models that are used to build a linear relationship between one response or dependent variable and more than one predictor or independent variable. The form of the equation that represents a multiple linear regression model is Y=b0+b1X1+ b2X2 + … + bnXn, where bi represents the coefficients of the ith predictor variable. In this type of linear regression model, each predictor variable has its own coefficient that is used to calculate the predicted value of the response variable.

While training linear regression models, the requirement is to determine the coefficients which can result in the best-fitted linear regression line. The learning algorithm used to find the most appropriate coefficients is known as least squares regression . In the least-squares regression method, the coefficients are calculated using the least-squares error function. The main objective of this method is to minimize or reduce the sum of squared residuals between actual and predicted response values. The sum of squared residuals is also called the residual sum of squares (RSS). The outcome of executing the least-squares regression method is coefficients that minimize the linear regression cost function .

The residual e of the ith observation is represented as the following where [latex]Y_i[/latex] is the ith observation and [latex]\hat{Y_i}[/latex] is the prediction for ith observation or the value of response variable for ith observation.

[latex]e_i = Y_i – \hat{Y_i}[/latex]

The residual sum of squares can be represented as the following:

[latex]RSS = e_1^2 + e_2^2 + e_3^2 + … + e_n^2[/latex]

The least-squares method represents the algorithm that minimizes the above term, RSS.

Once the coefficients are determined, can it be claimed that these coefficients are the most appropriate ones for linear regression? The answer is no. After all, the coefficients are only the estimates and thus, there will be standard errors associated with each of the coefficients. Recall that the standard error is used to calculate the confidence interval in which the mean value of the population parameter would exist. In other words, it represents the error of estimating a population parameter based on the sample data. The value of the standard error is calculated as the standard deviation of the sample divided by the square root of the sample size. The formula below represents the standard error of a mean.

[latex]SE(\mu) = \frac{\sigma}{\sqrt(N)}[/latex]

Thus, without analyzing aspects such as the standard error associated with the coefficients, it cannot be claimed that the linear regression coefficients are the most suitable ones without performing hypothesis testing. This is where hypothesis testing is needed . Before we get into why we need hypothesis testing with the linear regression model, let’s briefly learn about what is hypothesis testing?

Train a Multiple Linear Regression Model using R

Before getting into understanding the hypothesis testing concepts in relation to the linear regression model, let’s train a multi-variate or multiple linear regression model and print the summary output of the model which will be referred to, in the next section.

The data used for creating a multi-linear regression model is BostonHousing which can be loaded in RStudioby installing mlbench package. The code is shown below:

install.packages(“mlbench”) library(mlbench) data(“BostonHousing”)

Once the data is loaded, the code shown below can be used to create the linear regression model.

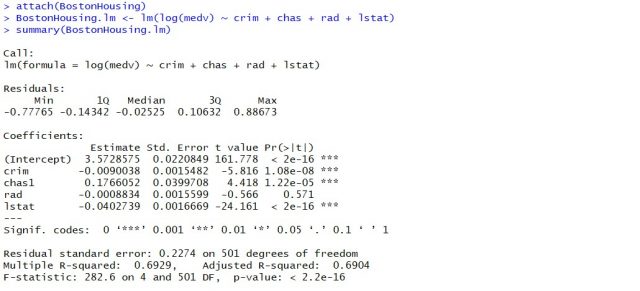
attach(BostonHousing) BostonHousing.lm <- lm(log(medv) ~ crim + chas + rad + lstat) summary(BostonHousing.lm)

Executing the above command will result in the creation of a linear regression model with the response variable as medv and predictor variables as crim, chas, rad, and lstat. The following represents the details related to the response and predictor variables:

log(medv) : Log of the median value of owner-occupied homes in USD 1000’s
crim : Per capita crime rate by town
chas : Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
rad : Index of accessibility to radial highways
lstat : Percentage of the lower status of the population

The following will be the output of the summary command that prints the details relating to the model including hypothesis testing details for coefficients (t-statistics) and the model as a whole (f-statistics)

linear regression model summary table r.png

Hypothesis tests & Linear Regression Models

Hypothesis tests are the statistical procedure that is used to test a claim or assumption about the underlying distribution of a population based on the sample data. Here are key steps of doing hypothesis tests with linear regression models:

Hypothesis formulation for T-tests: In the case of linear regression, the claim is made that there exists a relationship between response and predictor variables, and the claim is represented using the non-zero value of coefficients of predictor variables in the linear equation or regression model. This is formulated as an alternate hypothesis. Thus, the null hypothesis is set that there is no relationship between response and the predictor variables . Hence, the coefficients related to each of the predictor variables is equal to zero (0). So, if the linear regression model is Y = a0 + a1x1 + a2x2 + a3x3, then the null hypothesis for each test states that a1 = 0, a2 = 0, a3 = 0 etc. For all the predictor variables, individual hypothesis testing is done to determine whether the relationship between response and that particular predictor variable is statistically significant based on the sample data used for training the model. Thus, if there are, say, 5 features, there will be five hypothesis tests and each will have an associated null and alternate hypothesis.
Hypothesis formulation for F-test : In addition, there is a hypothesis test done around the claim that there is a linear regression model representing the response variable and all the predictor variables. The null hypothesis is that the linear regression model does not exist . This essentially means that the value of all the coefficients is equal to zero. So, if the linear regression model is Y = a0 + a1x1 + a2x2 + a3x3, then the null hypothesis states that a1 = a2 = a3 = 0.
F-statistics for testing hypothesis for linear regression model : F-test is used to test the null hypothesis that a linear regression model does not exist, representing the relationship between the response variable y and the predictor variables x1, x2, x3, x4 and x5. The null hypothesis can also be represented as x1 = x2 = x3 = x4 = x5 = 0. F-statistics is calculated as a function of sum of squares residuals for restricted regression (representing linear regression model with only intercept or bias and all the values of coefficients as zero) and sum of squares residuals for unrestricted regression (representing linear regression model). In the above diagram, note the value of f-statistics as 15.66 against the degrees of freedom as 5 and 194.
Evaluate t-statistics against the critical value/region : After calculating the value of t-statistics for each coefficient, it is now time to make a decision about whether to accept or reject the null hypothesis. In order for this decision to be made, one needs to set a significance level, which is also known as the alpha level. The significance level of 0.05 is usually set for rejecting the null hypothesis or otherwise. If the value of t-statistics fall in the critical region, the null hypothesis is rejected. Or, if the p-value comes out to be less than 0.05, the null hypothesis is rejected.
Evaluate f-statistics against the critical value/region : The value of F-statistics and the p-value is evaluated for testing the null hypothesis that the linear regression model representing response and predictor variables does not exist. If the value of f-statistics is more than the critical value at the level of significance as 0.05, the null hypothesis is rejected. This means that the linear model exists with at least one valid coefficients.
Draw conclusions : The final step of hypothesis testing is to draw a conclusion by interpreting the results in terms of the original claim or hypothesis. If the null hypothesis of one or more predictor variables is rejected, it represents the fact that the relationship between the response and the predictor variable is not statistically significant based on the evidence or the sample data we used for training the model. Similarly, if the f-statistics value lies in the critical region and the value of the p-value is less than the alpha value usually set as 0.05, one can say that there exists a linear regression model.

Why hypothesis tests for linear regression models?

The reasons why we need to do hypothesis tests in case of a linear regression model are following:

By creating the model, we are establishing a new truth (claims) about the relationship between response or dependent variable with one or more predictor or independent variables. In order to justify the truth, there are needed one or more tests. These tests can be termed as an act of testing the claim (or new truth) or in other words, hypothesis tests.
One kind of test is required to test the relationship between response and each of the predictor variables (hence, T-tests)
Another kind of test is required to test the linear regression model representation as a whole. This is called F-test.

While training linear regression models, hypothesis testing is done to determine whether the relationship between the response and each of the predictor variables is statistically significant or otherwise. The coefficients related to each of the predictor variables is determined. Then, individual hypothesis tests are done to determine whether the relationship between response and that particular predictor variable is statistically significant based on the sample data used for training the model. If at least one of the null hypotheses is rejected, it represents the fact that there exists no relationship between response and that particular predictor variable. T-statistics is used for performing the hypothesis testing because the standard deviation of the sampling distribution is unknown. The value of t-statistics is compared with the critical value from the t-distribution table in order to make a decision about whether to accept or reject the null hypothesis regarding the relationship between the response and predictor variables. If the value falls in the critical region, then the null hypothesis is rejected which means that there is no relationship between response and that predictor variable. In addition to T-tests, F-test is performed to test the null hypothesis that the linear regression model does not exist and that the value of all the coefficients is zero (0). Learn more about the linear regression and t-test in this blog – Linear regression t-test: formula, example .

Ajitesh Kumar

One response.

Very informative

ChatGPT Prompts (250+)

Generate Design Ideas for App
Expand Feature Set of App
Create a User Journey Map for App
Generate Visual Design Ideas for App
Generate a List of Competitors for App
How to Learn Effectively: A Holistic Approach
How to Choose Right Statistical Tests: Examples
Data Lakehouses Fundamentals & Examples
Machine Learning Lifecycle: Data to Deployment Example
Autoencoder vs Variational Autoencoder (VAE): Differences, Example

Data Science / AI Trends

• Prepend any arxiv.org link with talk2 to load the paper into a responsive chat application
• Custom LLM and AI Agents (RAG) On Structured + Unstructured Data - AI Brain For Your Organization
• Guides, papers, lecture, notebooks and resources for prompt engineering
• Common tricks to make LLMs efficient and stable
• Machine learning in finance

Free Online Tools

Create Scatter Plots Online for your Excel Data
Histogram / Frequency Distribution Creation Tool
Online Pie Chart Maker Tool
Z-test vs T-test Decision Tool
Independent samples t-test calculator

Hypothesis Test for Regression Slope

This lesson describes how to conduct a hypothesis test to determine whether there is a significant linear relationship between an independent variable X and a dependent variable Y .

The test focuses on the slope of the regression line

Y = Β 0 + Β 1 X

where Β 0 is a constant, Β 1 is the slope (also called the regression coefficient), X is the value of the independent variable, and Y is the value of the dependent variable.

If we find that the slope of the regression line is significantly different from zero, we will conclude that there is a significant relationship between the independent and dependent variables.

Test Requirements

The approach described in this lesson is valid whenever the standard requirements for simple linear regression are met.

The dependent variable Y has a linear relationship to the independent variable X .
For each value of X, the probability distribution of Y has the same standard deviation σ.
The Y values are independent.
The Y values are roughly normally distributed (i.e., symmetric and unimodal ). A little skewness is ok if the sample size is large.

The test procedure consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.

State the Hypotheses

If there is a significant linear relationship between the independent variable X and the dependent variable Y , the slope will not equal zero.

H o : Β 1 = 0

H a : Β 1 ≠ 0

The null hypothesis states that the slope is equal to zero, and the alternative hypothesis states that the slope is not equal to zero.

Formulate an Analysis Plan

The analysis plan describes how to use sample data to accept or reject the null hypothesis. The plan should specify the following elements.

Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
Test method. Use a linear regression t-test (described in the next section) to determine whether the slope of the regression line differs significantly from zero.

Analyze Sample Data

Using sample data, find the standard error of the slope, the slope of the regression line, the degrees of freedom, the test statistic, and the P-value associated with the test statistic. The approach described in this section is illustrated in the sample problem at the end of this lesson.

SE = s b 1 = sqrt [ Σ(y i - ŷ i ) 2 / (n - 2) ] / sqrt [ Σ(x i - x ) 2 ]

Slope. Like the standard error, the slope of the regression line will be provided by most statistics software packages. In the hypothetical output above, the slope is equal to 35.

t = b 1 / SE

P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a t statistic, use the t Distribution Calculator to assess the probability associated with the test statistic. Use the degrees of freedom computed above.

Interpret Results

If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Test Your Understanding

The local utility company surveys 101 randomly selected customers. For each survey participant, the company collects the following: annual electric bill (in dollars) and home size (in square feet). Output from a regression analysis appears below.

Is there a significant linear relationship between annual bill and home size? Use a 0.05 level of significance.

The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:

H o : The slope of the regression line is equal to zero.

H a : The slope of the regression line is not equal to zero.

Formulate an analysis plan . For this analysis, the significance level is 0.05. Using sample data, we will conduct a linear regression t-test to determine whether the slope of the regression line differs significantly from zero.

We get the slope (b 1 ) and the standard error (SE) from the regression output.

b 1 = 0.55 SE = 0.24

We compute the degrees of freedom and the t statistic, using the following equations.

DF = n - 2 = 101 - 2 = 99

t = b 1 /SE = 0.55/0.24 = 2.29

where DF is the degrees of freedom, n is the number of observations in the sample, b 1 is the slope of the regression line, and SE is the standard error of the slope.

Interpret results . Since the P-value (0.0242) is less than the significance level (0.05), we cannot accept the null hypothesis.

Chapter 8: Hypothesis Testing with One Sample

8.1 Null and Alternative Hypotheses

Learning objectives.

By the end of this section, the student should be able to:

Describe hypothesis testing in general and in practice.

Hypothesis Testing

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

H a : μ ≠ 2.0

H 0 : μ = 66
H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

H a : μ < 5

Ha: μ < 45

In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H0: p ≤ 0.066

Ha: p > 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : p = 0.40
H a : p > 0.40

Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm.

a statement about the value of a population parameter, in case of two hypotheses, the statement assumed to be true is called the null hypothesis (notation H0) and the contradictory statement is called the alternative hypothesis (notation Ha).

Share This Book

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

11.1: Testing the Hypothesis that β = 0

Last updated
Save as PDF
Page ID 26113

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

The correlation coefficient, $r$, tells us about the strength and direction of the linear relationship between $x$ and $y$. However, the reliability of the linear model also depends on how many observed data points are in the sample. We need to look at both the value of the correlation coefficient $r$ and the sample size $n$, together. We perform a hypothesis test of the "significance of the correlation coefficient" to decide whether the linear relationship in the sample data is strong enough to use to model the relationship in the population.

The sample data are used to compute $r$, the correlation coefficient for the sample. If we had data for the entire population, we could find the population correlation coefficient. But because we have only sample data, we cannot calculate the population correlation coefficient. The sample correlation coefficient, $r$, is our estimate of the unknown population correlation coefficient.

The symbol for the population correlation coefficient is $\rho$, the Greek letter "rho."
$\rho =$ population correlation coefficient (unknown)
$r =$ sample correlation coefficient (known; calculated from sample data)

The hypothesis test lets us decide whether the value of the population correlation coefficient $\rho$ is "close to zero" or "significantly different from zero". We decide this based on the sample correlation coefficient $r$ and the sample size $n$.

If the test concludes that the correlation coefficient is significantly different from zero, we say that the correlation coefficient is "significant."

Conclusion: There is sufficient evidence to conclude that there is a significant linear relationship between $x$ and $y$ because the correlation coefficient is significantly different from zero.
What the conclusion means: There is a significant linear relationship between $x$ and $y$. We can use the regression line to model the linear relationship between $x$ and $y$ in the population.

If the test concludes that the correlation coefficient is not significantly different from zero (it is close to zero), we say that correlation coefficient is "not significant".

Conclusion: "There is insufficient evidence to conclude that there is a significant linear relationship between $x$ and $y$ because the correlation coefficient is not significantly different from zero."
What the conclusion means: There is not a significant linear relationship between $x$ and $y$. Therefore, we CANNOT use the regression line to model a linear relationship between $x$ and $y$ in the population.
If $r$ is significant and the scatter plot shows a linear trend, the line can be used to predict the value of $y$ for values of $x$ that are within the domain of observed $x$ values.
If $r$ is not significant OR if the scatter plot does not show a linear trend, the line should not be used for prediction.
If $r$ is significant and if the scatter plot shows a linear trend, the line may NOT be appropriate or reliable for prediction OUTSIDE the domain of observed $x$ values in the data.

PERFORMING THE HYPOTHESIS TEST

Null Hypothesis: $H_{0}: \rho = 0$
Alternate Hypothesis: $H_{a}: \rho \neq 0$

WHAT THE HYPOTHESES MEAN IN WORDS:

Null Hypothesis $H_{0}$ : The population correlation coefficient IS NOT significantly different from zero. There IS NOT a significant linear relationship(correlation) between $x$ and $y$ in the population.
Alternate Hypothesis $H_{a}$ : The population correlation coefficient IS significantly DIFFERENT FROM zero. There IS A SIGNIFICANT LINEAR RELATIONSHIP (correlation) between $x$ and $y$ in the population.

DRAWING A CONCLUSION:There are two methods of making the decision. The two methods are equivalent and give the same result.

Method 1: Using the $p\text{-value}$
Method 2: Using a table of critical values

In this chapter of this textbook, we will always use a significance level of 5%, $\alpha = 0.05$

Using the $p\text{-value}$ method, you could choose any appropriate significance level you want; you are not limited to using $\alpha = 0.05$. But the table of critical values provided in this textbook assumes that we are using a significance level of 5%, $\alpha = 0.05$. (If we wanted to use a different significance level than 5% with the critical value method, we would need different tables of critical values that are not provided in this textbook.)

METHOD 1: Using a $p\text{-value}$ to make a decision

To calculate the $p\text{-value}$ using LinRegTTEST:

On the LinRegTTEST input screen, on the line prompt for $\beta$ or $\rho$, highlight "$\neq 0$"

The output screen shows the $p\text{-value}$ on the line that reads "$p =$".

(Most computer statistical software can calculate the $p\text{-value}$.)

If the $p\text{-value}$ is less than the significance level ( $\alpha = 0.05$ ):

Decision: Reject the null hypothesis.
Conclusion: "There is sufficient evidence to conclude that there is a significant linear relationship between $x$ and $y$ because the correlation coefficient is significantly different from zero."

If the $p\text{-value}$ is NOT less than the significance level ( $\alpha = 0.05$ )

Decision: DO NOT REJECT the null hypothesis.
Conclusion: "There is insufficient evidence to conclude that there is a significant linear relationship between $x$ and $y$ because the correlation coefficient is NOT significantly different from zero."

Calculation Notes:

You will use technology to calculate the $p\text{-value}$. The following describes the calculations to compute the test statistics and the $p\text{-value}$:
The $p\text{-value}$ is calculated using a $t$-distribution with $n - 2$ degrees of freedom.
The formula for the test statistic is $t = \frac{r\sqrt{n-2}}{\sqrt{1-r^{2}}}$. The value of the test statistic, $t$, is shown in the computer or calculator output along with the $p\text{-value}$. The test statistic $t$ has the same sign as the correlation coefficient $r$.
The $p\text{-value}$ is the combined area in both tails.

An alternative way to calculate the $p\text{-value}$ ( $p$ ) given by LinRegTTest is the command 2*tcdf(abs(t),10^99, n-2) in 2nd DISTR.

THIRD-EXAM vs FINAL-EXAM EXAMPLE: $p\text{-value}$ method

Consider the third exam/final exam example.
The line of best fit is: $\hat{y} = -173.51 + 4.83x$ with $r = 0.6631$ and there are $n = 11$ data points.
Can the regression line be used for prediction? Given a third exam score ( $x$ value), can we use the line to predict the final exam score (predicted $y$ value)?
$H_{0}: \rho = 0$
$H_{a}: \rho \neq 0$
$\alpha = 0.05$
The $p\text{-value}$ is 0.026 (from LinRegTTest on your calculator or from computer software).
The $p\text{-value}$, 0.026, is less than the significance level of $\alpha = 0.05$.
Decision: Reject the Null Hypothesis $H_{0}$
Conclusion: There is sufficient evidence to conclude that there is a significant linear relationship between the third exam score ($x$) and the final exam score ($y$) because the correlation coefficient is significantly different from zero.

Because $r$ is significant and the scatter plot shows a linear trend, the regression line can be used to predict final exam scores.

METHOD 2: Using a table of Critical Values to make a decision

The 95% Critical Values of the Sample Correlation Coefficient Table can be used to give you a good idea of whether the computed value of $r$ is significant or not . Compare $r$ to the appropriate critical value in the table. If $r$ is not between the positive and negative critical values, then the correlation coefficient is significant. If $r$ is significant, then you may want to use the line for prediction.

Example $\PageIndex{1}$

Suppose you computed $r = 0.801$ using $n = 10$ data points. $df = n - 2 = 10 - 2 = 8$. The critical values associated with $df = 8$ are $-0.632$ and $+0.632$. If $r <$ negative critical value or $r >$ positive critical value, then $r$ is significant. Since $r = 0.801$ and $0.801 > 0.632$, $r$ is significant and the line may be used for prediction. If you view this example on a number line, it will help you.

Exercise $\PageIndex{1}$

For a given line of best fit, you computed that $r = 0.6501$ using $n = 12$ data points and the critical value is 0.576. Can the line be used for prediction? Why or why not?

If the scatter plot looks linear then, yes, the line can be used for prediction, because $r >$ the positive critical value.

Example $\PageIndex{2}$

Suppose you computed $r = –0.624$ with 14 data points. $df = 14 – 2 = 12$. The critical values are $-0.532$ and $0.532$. Since $-0.624 < -0.532$, $r$ is significant and the line can be used for prediction

Exercise $\PageIndex{2}$

For a given line of best fit, you compute that $r = 0.5204$ using $n = 9$ data points, and the critical value is $0.666$. Can the line be used for prediction? Why or why not?

No, the line cannot be used for prediction, because $r <$ the positive critical value.

Example $\PageIndex{3}$

Suppose you computed $r = 0.776$ and $n = 6$. $df = 6 - 2 = 4$. The critical values are $-0.811$ and $0.811$. Since $-0.811 < 0.776 < 0.811$, $r$ is not significant, and the line should not be used for prediction.

Exercise $\PageIndex{3}$

For a given line of best fit, you compute that $r = -0.7204$ using $n = 8$ data points, and the critical value is $= 0.707$. Can the line be used for prediction? Why or why not?

Yes, the line can be used for prediction, because $r <$ the negative critical value.

THIRD-EXAM vs FINAL-EXAM EXAMPLE: critical value method

Consider the third exam/final exam example. The line of best fit is: $\hat{y} = -173.51 + 4.83x$ with $r = 0.6631$ and there are $n = 11$ data points. Can the regression line be used for prediction? Given a third-exam score ( $x$ value), can we use the line to predict the final exam score (predicted $y$ value)?

Use the "95% Critical Value" table for $r$ with $df = n - 2 = 11 - 2 = 9$.
The critical values are $-0.602$ and $+0.602$
Since $0.6631 > 0.602$, $r$ is significant.
Conclusion:There is sufficient evidence to conclude that there is a significant linear relationship between the third exam score ($x$) and the final exam score ($y$) because the correlation coefficient is significantly different from zero.

Example $\PageIndex{4}$

Suppose you computed the following correlation coefficients. Using the table at the end of the chapter, determine if $r$ is significant and the line of best fit associated with each r can be used to predict a $y$ value. If it helps, draw a number line.

$r = –0.567$ and the sample size, $n$, is $19$. The $df = n - 2 = 17$. The critical value is $-0.456$. $-0.567 < -0.456$ so $r$ is significant.
$r = 0.708$ and the sample size, $n$, is $9$. The $df = n - 2 = 7$. The critical value is $0.666$. $0.708 > 0.666$ so $r$ is significant.
$r = 0.134$ and the sample size, $n$, is $14$. The $df = 14 - 2 = 12$. The critical value is $0.532$. $0.134$ is between $-0.532$ and $0.532$ so $r$ is not significant.
$r = 0$ and the sample size, $n$, is five. No matter what the $dfs$ are, $r = 0$ is between the two critical values so $r$ is not significant.

Exercise $\PageIndex{4}$

For a given line of best fit, you compute that $r = 0$ using $n = 100$ data points. Can the line be used for prediction? Why or why not?

No, the line cannot be used for prediction no matter what the sample size is.

Assumptions in Testing the Significance of the Correlation Coefficient

Testing the significance of the correlation coefficient requires that certain assumptions about the data are satisfied. The premise of this test is that the data are a sample of observed points taken from a larger population. We have not examined the entire population because it is not possible or feasible to do so. We are examining the sample to draw a conclusion about whether the linear relationship that we see between $x$ and $y$ in the sample data provides strong enough evidence so that we can conclude that there is a linear relationship between $x$ and $y$ in the population.

The regression line equation that we calculate from the sample data gives the best-fit line for our particular sample. We want to use this best-fit line for the sample as an estimate of the best-fit line for the population. Examining the scatter plot and testing the significance of the correlation coefficient helps us determine if it is appropriate to do this.

The assumptions underlying the test of significance are:

There is a linear relationship in the population that models the average value of $y$ for varying values of $x$. In other words, the expected value of $y$ for each particular value lies on a straight line in the population. (We do not know the equation for the line for the population. Our regression line from the sample is our best estimate of this line in the population.)
The $y$ values for any particular $x$ value are normally distributed about the line. This implies that there are more $y$ values scattered closer to the line than are scattered farther away. Assumption (1) implies that these normal distributions are centered on the line: the means of these normal distributions of $y$ values lie on the line.
The standard deviations of the population $y$ values about the line are equal for each value of $x$. In other words, each of these normal distributions of $y$ values has the same shape and spread about the line.
The residual errors are mutually independent (no pattern).
The data are produced from a well-designed, random sample or randomized experiment.

Linear regression is a procedure for fitting a straight line of the form $\hat{y} = a + bx$ to data. The conditions for regression are:

Linear In the population, there is a linear relationship that models the average value of $y$ for different values of $x$.
Independent The residuals are assumed to be independent.
Normal The $y$ values are distributed normally for any value of $x$.
Equal variance The standard deviation of the $y$ values is equal for each $x$ value.
Random The data are produced from a well-designed random sample or randomized experiment.

The slope $b$ and intercept $a$ of the least-squares line estimate the slope $\beta$ and intercept $\alpha$ of the population (true) regression line. To estimate the population standard deviation of $y$, $\sigma$, use the standard deviation of the residuals, $s$. $s = \sqrt{\frac{SEE}{n-2}}$. The variable $\rho$ (rho) is the population correlation coefficient. To test the null hypothesis $H_{0}: \rho =$ hypothesized value , use a linear regression t-test. The most common null hypothesis is $H_{0}: \rho = 0$ which indicates there is no linear relationship between $x$ and $y$ in the population. The TI-83, 83+, 84, 84+ calculator function LinRegTTest can perform this test (STATS TESTS LinRegTTest).

Formula Review

Least Squares Line or Line of Best Fit:

\[\hat{y} = a + bx\]

\[a = y\text{-intercept}\]

\[b = \text{slope}\]

Standard deviation of the residuals:

\[s = \sqrt{\frac{SEE}{n-2}}\]

\[SSE = \text{sum of squared errors}\]

\[n = \text{the number of data points}\]

Lesson 5: Multiple Linear Regression (MLR) Model & Evaluation

Overview of this lesson.

In this lesson, we make our first (and last?!) major jump in the course. We move from the simple linear regression model with one predictor to the multiple linear regression model with two or more predictors. That is, we use the adjective "simple" to denote that our model has only predictor, and we use the adjective "multiple" to indicate that our model has at least two predictors.

In the multiple regression setting, because of the potentially large number of predictors, it is more efficient to use matrices to define the regression model and the subsequent analyses. This lesson considers some of the more important multiple regression formulas in matrix form. If you're unsure about any of this, it may be a good time to take a look at this Matrix Algebra Review .

The good news is that everything you learned about the simple linear regression model extends — with at most minor modification — to the multiple linear regression model. Think about it — you don't have to forget all of that good stuff you learned! In particular:

The models have similar "LINE" assumptions. The only real difference is that whereas in simple linear regression we think of the distribution of errors at a fixed value of the single predictor, with multiple linear regression we have to think of the distribution of errors at a fixed set of values for all the predictors. All of the model checking procedures we learned earlier are useful in the multiple linear regression framework, although the process becomes more involved since we now have multiple predictors. We'll explore this issue further in Lesson 6.
The use and interpretation of r 2 (which we'll denote R 2 in the context of multiple linear regression) remains the same. However, with multiple linear regression we can also make use of an "adjusted" R 2 value, which is useful for model building purposes. We'll explore this measure further in Lesson 11.
With a minor generalization of the degrees of freedom, we use t -tests and t -intervals for the regression slope coefficients to assess whether a predictor is significantly linearly related to the response, after controlling for the effects of all the opther predictors in the model.
With a minor generalization of the degrees of freedom, we use confidence intervals for estimating the mean response and prediction intervals for predicting an individual response. We'll explore these further in Lesson 6.

For the simple linear regression model, there is only one slope parameter about which one can perform hypothesis tests. For the multiple linear regression model, there are three different hypothesis tests for slopes that one could conduct. They are:

a hypothesis test for testing that one slope parameter is 0
a hypothesis test for testing that all of the slope parameters are 0
a hypothesis test for testing that a subset — more than one, but not all — of the slope parameters are 0

In this lesson, we also learn how to perform each of the above three hypothesis tests.

5.1 - Example on IQ and Physical Characteristics
5.2 - Example on Underground Air Quality
5.3 - The Multiple Linear Regression Model
5.4 - A Matrix Formulation of the Multiple Regression Model
5.5 - Three Types of MLR Parameter Tests
5.6 - The General Linear F-Test
5.7 - MLR Parameter Tests
5.8 - Partial R-squared
5.9 - Further MLR Examples

Start Here!

Welcome to STAT 462!
Search Course Materials
Lesson 1: Statistical Inference Foundations
Lesson 2: Simple Linear Regression (SLR) Model
Lesson 3: SLR Evaluation
Lesson 4: SLR Assumptions, Estimation & Prediction
5.9- Further MLR Examples
Lesson 6: MLR Assumptions, Estimation & Prediction
Lesson 7: Transformations & Interactions
Lesson 8: Categorical Predictors
Lesson 9: Influential Points
Lesson 10: Regression Pitfalls
Lesson 11: Model Building
Lesson 12: Logistic, Poisson & Nonlinear Regression
Website for Applied Regression Modeling, 2nd edition
Notation Used in this Course
R Software Help
Minitab Software Help

What is the purpose and significance of the t-test in linear regression analysis?

Table of Contents

null and alternative hypothesis for linear regression

The t-test is a statistical tool used in linear regression analysis to determine the significance of the relationship between two variables. It helps to determine whether the observed relationship between the dependent and independent variables is statistically significant or if it occurred by chance. This is important in understanding the strength and direction of the relationship between the variables, and it helps to make informed decisions on the variables to include in the regression model. Additionally, the t-test allows for the identification of any potential errors or flaws in the data, ensuring the accuracy and validity of the regression results. Overall, the t-test is a crucial tool in linear regression analysis as it helps to assess the significance of the relationship between variables and aids in making sound and reliable conclusions.

Understanding the t-Test in Linear Regression

Linear regression is used to quantify the relationship between a predictor variable and a response variable.

Whenever we perform linear regression, we want to know if there is a statistically significant relationship between the predictor variable and the response variable.

We test for significance by performing a t-test for the regression slope. We use the following null and alternative hypothesis for this t-test:

H 0 : β 1 = 0 (the slope is equal to zero)
H A : β 1 ≠ 0 (the slope is not equal to zero)

We then calculate the test statistic as follows:

t = b / SE b
b : coefficient estimate
SE b : standard error of the coefficient estimate

If the p-value that corresponds to t is less than some threshold (e.g. α = .05) then we reject the null hypothesis and conclude that there is a statistically significant relationship between the predictor variable and the response variable.

The following example shows how to perform a t-test for a linear regression model in practice.

Example: Performing a t-Test for Linear Regression

Suppose a professor wants to analyze the relationship between hours studied and exam score received for 40 of his students.

He performs simple linear regression using hours studied as the predictor variable and exam score received as the response variable.

The following table shows the results of the regression model:

To determine if hours studied has a statistically significant relationship with final exam score, we can perform a t-test.

We use the following null and alternative hypothesis for this t-test:

H 0 : β 1 = 0 (the slope for hours studied is equal to zero)
H A : β 1 ≠ 0 (the slope for hours studied is not equal to zero)
t = 1.117 / 1.025

The p-value that corresponds to t = 1.089 with df = n-2 = 40 – 2 = 38 is 0.283 .

Note that we can also use the to calculate this p-value:

Since this p-value is not less than .05, we fail to reject the null hypothesis.

This means that hours studied does not have a statistically significant relationship between final exam score.

Additional Resources

The following tutorials offer additional information about linear regression:

Related terms:

1. Customer Segmentation in Marketing: Companies often use cluster analysis to group customers based on their demographics, behavior, and preferences. This helps them tailor their marketing strategies and target specific customer segments. 2. Disease Clustering in Healthcare: Cluster analysis is used in healthcare to identify patterns and clusters of diseases in a population. This can help in understanding the spread of diseases and developing targeted prevention and treatment methods. 3. Fraud Detection in Banking: Banks and financial institutions use cluster analysis to identify patterns of fraudulent activities and detect anomalies in transactions. This helps in preventing fraud and protecting customers’ financial assets. 4. Image and Text Clustering in Social Media: Social media platforms use cluster analysis to group similar images, videos, and text posts together. This helps in organizing and recommending relevant content to users based on their interests and preferences. 5. Crime Analysis in Law Enforcement: Police departments use cluster analysis to identify high-crime areas and patterns of criminal activities. This helps in deploying resources effectively and preventing crime in specific areas.
What is the meaning and significance of P-values and statistical significance in statistical analysis?
What is a Residuals vs. Leverage Plot? (Definition & Example) A Residuals vs. Leverage Plot is a graphical representation used in regression analysis to assess the influence of individual data points on the overall model fit. It plots the standardized residuals (vertical axis) against the leverage values (horizontal axis) for each data point in the dataset. The standardized residual represents the difference between the observed and predicted values, divided by the standard error of the regression. It helps identify unusual observations or outliers that may have a significant impact on the regression model. The leverage value, on the other hand, measures how much influence a data point has on the estimated regression coefficients. It is calculated based on the distance of a data point from the center of the predictor variables. In a Residuals vs. Leverage Plot, a data point with a high leverage value and a large standardized residual indicates that it has a significant impact on the model fit. This can be due to extreme values or influential observations that are not well represented by the model. An example of a Residuals vs. Leverage Plot is shown below: [Image of a Residuals vs. Leverage Plot] In this example, the outliers are represented by the data points with high standardized residuals and leverage values, as they deviate significantly from the overall pattern of the data. These points may need to be further investigated and potentially excluded from the model if they are found to be influential.
What is the difference between statistical significance and practical significance?
What is the purpose of classification and regression trees and how are they used in data analysis?
What is the purpose of Bartlett’s Test of Sphericity and how is it used in statistical analysis?
What is the F-test of overall significance in regression and how can it be understood?
How can multiple linear regression be used for predictive analysis in Excel?
What is the significance of the message “glm.fit: fitted probabilities numerically 0 or 1 occurred” in statistical analysis?
What is the significance of the F-value and p-value in ANOVA and how do they help interpret the results of the analysis?

IMAGES

Difference between Null and Alternative Hypothesis
Hypothesis Test for Simple Linear Regession
Mod-01 Lec-39 Hypothesis Testing in Linear Regression
Null Hypothesis and Alternative Hypothesis
PPT
Understanding the Null Hypothesis for Linear Regression

VIDEO

Testing of Hypothesis,Null, alternative hypothesis, type-I & -II Error etc @VATAMBEDUSRAVANKUMAR
Null & Alternative Hypothesis |Statistical Hypothesis #hypothesis #samplingdistribution #statistics
Null Hypothesis vs Alternate Hypothesis
Linear Regression
Linear regression for economists: The t-test
Statistics and probability

COMMENTS

Understanding the Null Hypothesis for Linear Regression
x: The value of the predictor variable. Simple linear regression uses the following null and alternative hypotheses: H0: β1 = 0. HA: β1 ≠ 0. The null hypothesis states that the coefficient β1 is equal to zero. In other words, there is no statistically significant relationship between the predictor variable, x, and the response variable, y.
12.2.1: Hypothesis Test for Linear Regression
The null hypothesis of a two-tailed test states that there is not a linear relationship between $x$ and $y$. The alternative hypothesis of a two-tailed test states that there is a significant linear relationship between $x$ and $y$. Either a t-test or an F-test may be used to see if the slope is significantly different from zero.
PDF Chapter 9 Simple Linear Regression
218 CHAPTER 9. SIMPLE LINEAR REGRESSION 9.2 Statistical hypotheses For simple linear regression, the chief null hypothesis is H 0: β 1 = 0, and the corresponding alternative hypothesis is H 1: β 1 6= 0. If this null hypothesis is true, then, from E(Y) = β 0 + β 1x we can see that the population mean of Y is β 0 for
Null & Alternative Hypotheses
You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test. ... Linear regression: There is a relationship ...
15.5: Hypothesis Tests for Regression Models
Formally, our "null model" corresponds to the fairly trivial "regression" model in which we include 0 predictors, and only include the intercept term b 0. H 0 :Y i =b 0 +ϵ i. If our regression model has K predictors, the "alternative model" is described using the usual formula for a multiple regression model: H1: Yi = (∑K k=1 ...
13.6 Testing the Regression Coefficients
Simple Linear Regression and Correlation. ... This is the claim for the null hypothesis in an individual regression coefficient test: [latex]H_0: \beta_i=0[/latex]. Relationship. ... =0.0082 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 5% significance level there is enough evidence to ...
3.3.4: Hypothesis Test for Simple Linear Regression
In simple linear regression, this is equivalent to saying "Are X an Y correlated?". In reviewing the model, Y = β0 +β1X + ε Y = β 0 + β 1 X + ε, as long as the slope ( β1 β 1) has any non‐zero value, X X will add value in helping predict the expected value of Y Y. However, if there is no correlation between X and Y, the value of ...
6.4
For the multiple linear regression model, there are three different hypothesis tests for slopes that one could conduct. They are: Hypothesis test for testing that all of the slope parameters are 0. Hypothesis test for testing that a subset — more than one, but not all — of the slope parameters are 0.
Understanding the Null Hypothesis for Linear Regression
Multiple linear regression uses the following null and alternative hypotheses: H 0: β 1 = β 2 = … = β k = 0; H A: β 1 = β 2 = … = β k ≠ 0; The null hypothesis states that all coefficients in the model are equal to zero. In other words, none of the predictor variables have a statistically significant relationship with the response ...
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
How to Test the Significance of a Regression Slope
Conducting a Hypothesis Test for a Regression Slope. To conduct a hypothesis test for a regression slope, we follow the standard five steps for any hypothesis test: Step 1. State the hypotheses. The null hypothesis (H0): B 1 = 0. The alternative hypothesis: (Ha): B 1 ≠ 0. Step 2. Determine a significance level to use.
Using a P-value to make conclusions in a test about slope
And so our null hypothesis is that Beta's equal to zero, and the alternative hypothesis, which is her suspicion, is that the true slope of the regression line is actually greater than zero. "Assume that all conditions for inference have been met."
Linear regression hypothesis testing: Concepts, Examples
Here are key steps of doing hypothesis tests with linear regression models: Formulate null and alternate hypotheses: The first step of hypothesis testing is to formulate the null and alternate hypotheses. The null hypothesis (H0) is a statement that represents the state of the real world where the truth about something needs to be justified.
Null and Alternative hypothesis for multiple linear regression
I have 1 dependent variable and 3 independent variables. I run multiple regression, and find that the p value for one of the independent variables is higher than 0.05 (95% is my confidence level).
PDF Lecture 5 Hypothesis Testing in Multiple Linear Regression
As in simple linear regression, under the null hypothesis t 0 = βˆ j seˆ(βˆ j) ∼ t n−p−1. We reject H 0 if |t 0| > t n−p−1,1−α/2. This is a partial test because βˆ j depends on all of the other predictors x i, i 6= j that are in the model. Thus, this is a test of the contribution of x j given the other predictors in the model.
9.1: Null and Alternative Hypotheses
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. $H_0$: The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
Hypothesis Test for Regression Slope
Hypothesis Test for Regression Slope. This lesson describes how to conduct a hypothesis test to determine whether there is a significant linear relationship between an independent variable X and a dependent variable Y.. The test focuses on the slope of the regression line Y = Β 0 + Β 1 X. where Β 0 is a constant, Β 1 is the slope (also called the regression coefficient), X is the value of ...
What is a null model in regression and how does it relate to the null
In regression, as described partially in the other two answers, the null model is the null hypothesis that all the regression parameters are 0. So you can interpret this as saying that under the null hypothesis, there is no trend and the best estimate/predictor of a new observation is the mean, which is 0 in the case of no intercept.
8.1 Null and Alternative Hypotheses
Hypothesis Testing. The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0: The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.
11.1: Testing the Hypothesis that β = 0
METHOD 1: Using a p-value to make a decision. To calculate the p-value using LinRegTTEST: On the LinRegTTEST input screen, on the line prompt for β or ρ, highlight " ≠ 0 ". The output screen shows the p-value on the line that reads " p = ". (Most computer statistical software can calculate the p-value .)
Lesson 5: Multiple Linear Regression (MLR) Model & Evaluation
For the simple linear regression model, there is only one slope parameter about which one can perform hypothesis tests. For the multiple linear regression model, there are three different hypothesis tests for slopes that one could conduct. ... Know how to specify the null and alternative hypotheses and be able to draw a conclusion given ...
Why does null hypothesis in simple linear regression (i.e. slope = 0
Why does null hypothesis in simple linear regression (i.e. slope = 0) have distribution? A null hypothesis is not a random variable; it doesn't have a distribution. A test statistic has a distribution. In particular we can compute what the distribution of some test statistic would be if the null hypothesis were true.
What is the purpose and significance of the t-test in linear regression
Whenever we perform linear regression, we want to know if there is a statistically significant relationship between the predictor variable and the response variable. We test for significance by performing a t-test for the regression slope. We use the following null and alternative hypothesis for this t-test: H 0: β 1 = 0 (the slope is equal to ...

13.6 Testing the Regression Coefficients

Testing the Regression Coefficients

Steps to Conduct a Hypothesis Test on a Regression Coefficient

Concept Review

Understanding the Null Hypothesis for Linear Regression

Example 1: Simple Linear Regression

Example 2: Multiple Linear Regression

Additional Resources

The Complete Guide: How to Report Regression Results

9.1 Null and Alternative Hypotheses

Example 9.1

Example 9.2

Example 9.3

Example 9.4

Collaborative Exercise

How to Test the Significance of a Regression Slope

Constructing a Confidence Interval for a Regression Slope

Conducting a Hypothesis Test for a Regression Slope

Featured Posts

4 Replies to “How to Test the Significance of a Regression Slope”

Leave a Reply Cancel reply

Join the Statology Community

Linear regression hypothesis testing: Concepts, Examples

What are linear regression models?

Train a Multiple Linear Regression Model using R

Hypothesis tests & Linear Regression Models

Why hypothesis tests for linear regression models?

Recent Posts

Ajitesh Kumar

Leave a Reply Cancel reply

ChatGPT Prompts (250+)

Data Science / AI Trends

Free Online Tools

Recent Comments

Hypothesis Test for Regression Slope

Test Requirements

State the Hypotheses

Formulate an Analysis Plan

Analyze Sample Data

Interpret Results

Test Your Understanding

8.1 Null and Alternative Hypotheses

Hypothesis Testing

Share This Book

Margin Size

11.1: Testing the Hypothesis that β = 0

PERFORMING THE HYPOTHESIS TEST

METHOD 1: Using a \(p\text{-value}\) to make a decision

METHOD 2: Using a table of Critical Values to make a decision

THIRD-EXAM vs FINAL-EXAM EXAMPLE: critical value method

Assumptions in Testing the Significance of the Correlation Coefficient

Formula Review

Lesson 5: Multiple Linear Regression (MLR) Model & Evaluation

Start Here!

What is the purpose and significance of the t-test in linear regression analysis?

Understanding the t-Test in Linear Regression

Example: Performing a t-Test for Linear Regression

Additional Resources

Related terms:

IMAGES

VIDEO

COMMENTS