what is a conditional hypothesis

Conditional Statement – Definition, Truth Table, Examples, FAQs

What is a conditional statement, how to write a conditional statement, what is a biconditional statement, solved examples on conditional statements, practice problems on conditional statements, frequently asked questions about conditional statements.

A conditional statement is a statement that is written in the “If p, then q” format. Here, the statement p is called the hypothesis and q is called the conclusion. It is a fundamental concept in logic and mathematics. 

Conditional statement symbol :  p → q

A conditional statement consists of two parts.

• The “if” clause, which presents a condition or hypothesis.
• The “then” clause, which indicates the consequence or result that follows if the condition is true. 

Example : If you brush your teeth, then you won’t get cavities.

Hypothesis (Condition): If you brush your teeth

Conclusion (Consequence): then you won’t get cavities 

Conditional Statement: Definition

A conditional statement is characterized by the presence of “if” as an antecedent and “then” as a consequent. A conditional statement, also known as an “if-then” statement consists of two parts:

• The “if” clause (hypothesis): This part presents a condition, situation, or assertion. It is the initial condition that is being considered.
• The “then” clause (conclusion): This part indicates the consequence, result, or action that will occur if the condition presented in the “if” clause is true or satisfied. 

Related Worksheets

Representation of Conditional Statement

The conditional statement of the form ‘If p, then q” is represented as p → q. 

It is pronounced as “p implies q.”

Different ways to express a conditional statement are:

• p implies q
• p is sufficient for q
• q is necessary for p

Parts of a Conditional Statement

There are two parts of conditional statements, hypothesis and conclusion. The hypothesis or condition will begin with the “if” part, and the conclusion or action will begin with the “then” part. A conditional statement is also called “implication.”

Conditional Statements Examples:

Example 1: If it is Sunday, then you can go to play. 

Hypothesis: If it is Sunday

Conclusion: then you can go to play. 

Example 2: If you eat all vegetables, then you can have the dessert.

Condition: If you eat all vegetables

Conclusion: then you can have the dessert 

To form a conditional statement, follow these concise steps:

Step 1 : Identify the condition (antecedent or “if” part) and the consequence (consequent or “then” part) of the statement.

Step 2 : Use the “if… then…” structure to connect the condition and consequence.

Step 3 : Ensure the statement expresses a logical relationship where the condition leads to the consequence.

Example 1 : “If you study (condition), then you will pass the exam (consequence).” 

This conditional statement asserts that studying leads to passing the exam. If you study (condition is true), then you will pass the exam (consequence is also true).

Example 2 : If you arrange the numbers from smallest to largest, then you will have an ascending order.

Hypothesis: If you arrange the numbers from smallest to largest

Conclusion: then you will have an ascending order

Truth Table for Conditional Statement

The truth table for a conditional statement is a table used in logic to explore the relationship between the truth values of two statements. It lists all possible combinations of truth values for “p” and “q” and determines whether the conditional statement is true or false for each combination. 

The truth value of p → q is false only when p is true and q is False. 

If the condition is false, the consequence doesn’t affect the truth of the conditional; it’s always true.

In all the other cases, it is true.

The truth table is helpful in the analysis of possible combinations of truth values for hypothesis or condition and conclusion or action. It is useful to understand the presence of truth or false statements. 

Converse, Inverse, and Contrapositive

The converse, inverse, and contrapositive are three related conditional statements that are derived from an original conditional statement “p → q.” 

Consider a conditional statement: If I run, then I feel great.

• Converse: 

The converse of “p → q” is “q → p.” It reverses the order of the original statement. While the original statement says “if p, then q,” the converse says “if q, then p.” 

Converse: If I feel great, then I run.

• Inverse: 

The inverse of “p → q” is “~p → ~q,” where “” denotes negation (opposite). It negates both the antecedent (p) and the consequent (q). So, if the original statement says “if p, then q,” the inverse says “if not p, then not q.”

Inverse : If I don’t run, then I don’t feel great.

• Contrapositive: 

The contrapositive of “p → q” is “~q → ~p.” It reverses the order and also negates both the statements. So, if the original statement says “if p, then q,” the contrapositive says “if not q, then not p.”

Contrapositive: If I don’t feel great, then I don’t run.

A biconditional statement is a type of compound statement in logic that expresses a bidirectional or two-way relationship between two statements. It asserts that “p” is true if and only if “q” is true, and vice versa. In symbolic notation, a biconditional statement is represented as “p ⟺ q.”

In simpler terms, a biconditional statement means that the truth of “p” and “q” are interdependent. 

If “p” is true, then “q” must also be true, and if “q” is true, then “p” must be true. Conversely, if “p” is false, then “q” must be false, and if “q” is false, then “p” must be false. 

Biconditional statements are often used to express equality, equivalence, or conditions where two statements are mutually dependent for their truth values. 

Examples : 

• I will stop my bike if and only if the traffic light is red.  
• I will stay if and only if you play my favorite song.

Facts about Conditional Statements

• The negation of a conditional statement “p → q” is expressed as “p and not q.” It is denoted as “𝑝 ∧ ∼𝑞.” 
• The conditional statement is not logically equivalent to its converse and inverse.
• The conditional statement is logically equivalent to its contrapositive. 
• Thus, we can write p → q ∼q → ∼p

In this article, we learned about the fundamentals of conditional statements in mathematical logic, including their structure, parts, truth tables, conditional logic examples, and various related concepts. Understanding conditional statements is key to logical reasoning and problem-solving. Now, let’s solve a few examples and practice MCQs for better comprehension.

Example 1: Identify the hypothesis and conclusion. 

If you sing, then I will dance.

Solution : 

Given statement: If you sing, then I will dance.

Here, the antecedent or the hypothesis is “if you sing.”

The conclusion is “then I will dance.”

Example 2: State the converse of the statement: “If the switch is off, then the machine won’t work.” 

Here, p: The switch is off

q: The machine won’t work.

The conditional statement can be denoted as p → q.

Converse of p → q is written by reversing the order of p and q in the original statement.

Converse of  p → q is q → p.

Converse of  p → q: q → p: If the machine won’t work, then the switch is off.

Example 3: What is the truth value of the given conditional statement? 

If 2+2=5 , then pigs can fly.

Solution:  

q: Pigs can fly.

The statement p is false. Now regardless of the truth value of statement q, the overall statement will be true. 

F → F = T

Hence, the truth value of the statement is true. 

Conditional Statement - Definition, Truth Table, Examples, FAQs

Attend this quiz & Test your knowledge.

What is the antecedent in the given conditional statement? If it’s sunny, then I’ll go to the beach.

A conditional statement can be expressed as, what is the converse of “a → b”, when the antecedent is true and the consequent is false, the conditional statement is.

What is the meaning of conditional statements?

Conditional statements, also known as “if-then” statements, express a cause-and-effect or logical relationship between two propositions.

When does the truth value of a conditional statement is F?

A conditional statement is considered false when the antecedent is true and the consequent is false.

What is the contrapositive of a conditional statement?

The contrapositive reverses the order of the statements and also negates both the statements. It is equivalent in truth value to the original statement.

RELATED POSTS

• Ordering Decimals: Definition, Types, Examples
• Decimal to Octal: Steps, Methods, Conversion Table
• Lattice Multiplication – Definition, Method, Examples, Facts, FAQs
• X Intercept – Definition, Formula, Graph, Examples
• Lateral Face – Definition With Examples

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.11: If Then Statements

• Last updated
• Save as PDF
• Page ID 2144

Hypothesis followed by a conclusion in a conditional statement.

Conditional Statements

A conditional statement (also called an if-then statement ) is a statement with a hypothesis followed by a conclusion . The hypothesis is the first, or “if,” part of a conditional statement. The conclusion is the second, or “then,” part of a conditional statement. The conclusion is the result of a hypothesis.

If-then statements might not always be written in the “if-then” form. Here are some examples of conditional statements:

• Statement 1: If you work overtime, then you’ll be paid time-and-a-half.
• Statement 2: I’ll wash the car if the weather is nice.
• Statement 3: If 2 divides evenly into \(x\), then \(x\) is an even number.
• Statement 4: I’ll be a millionaire when I win the lottery.
• Statement 5: All equiangular triangles are equilateral.

Statements 1 and 3 are written in the “if-then” form. The hypothesis of Statement 1 is “you work overtime.” The conclusion is “you’ll be paid time-and-a-half.” Statement 2 has the hypothesis after the conclusion. If the word “if” is in the middle of the statement, then the hypothesis is after it. The statement can be rewritten: If the weather is nice, then I will wash the car. Statement 4 uses the word “when” instead of “if” and is like Statement 2. It can be written: If I win the lottery, then I will be a millionaire. Statement 5 “if” and “then” are not there. It can be rewritten: If a triangle is equiangular, then it is equilateral.

What if you were given a statement like "All squares are rectangles"? How could you determine the hypothesis and conclusion of this statement?

Example \(\PageIndex{1}\)

Determine the hypothesis and conclusion: I'll bring an umbrella if it rains.

Hypothesis: "It rains." Conclusion: "I'll bring an umbrella."

Example \(\PageIndex{2}\)

Determine the hypothesis and conclusion: All right angles are \(90^{\circ}\).

Hypothesis: "An angle is right." Conclusion: "It is \(90^{\circ}\)."

Example \(\PageIndex{3}\)

Use the statement: I will graduate when I pass Calculus.

Rewrite in if-then form and determine the hypothesis and conclusion.

This statement can be rewritten as If I pass Calculus, then I will graduate. The hypothesis is “I pass Calculus,” and the conclusion is “I will graduate.”

Example \(\PageIndex{4}\)

Use the statement: All prime numbers are odd.

Rewrite in if-then form, determine the hypothesis and conclusion, and determine whether this is a true statement.

This statement can be rewritten as If a number is prime, then it is odd. The hypothesis is "a number is prime" and the conclusion is "it is odd". This is not a true statement (remember that not all conditional statements will be true!) since 2 is a prime number but it is not odd.

Example \(\PageIndex{5}\)

Determine the hypothesis and conclusion: Sarah will go to the store if Riley does the laundry.

The statement can be rewritten as "If Riley does the laundry then Sarah will go to the store." The hypothesis is "Riley does the laundry" and the conclusion is "Sarah will go to the store."

Determine the hypothesis and the conclusion for each statement.

• If 5 divides evenly into \(x\), then \(x\) ends in 0 or 5.
• If a triangle has three congruent sides, it is an equilateral triangle.
• Three points are coplanar if they all lie in the same plane.
• If \(x=3\), then \(x^2=9\).
• If you take yoga, then you are relaxed.
• All baseball players wear hats.
• I'll learn how to drive when I am 16 years old.
• If you do your homework, then you can watch TV.
• Alternate interior angles are congruent if lines are parallel.
• All kids like ice cream.

Additional Resources

Video: If-Then Statements Principles - Basic

Activities: If-Then Statements Discussion Questions

Study Aids: Conditional Statements Study Guide

Practice: If Then Statements

Real World: If Then Statements

Calcworkshop

Conditional Statement If Then's Defined in Geometry - 15+ Examples!

// Last Updated: January 21, 2020 - Watch Video //

In today’s geometry lesson , you’re going to learn all about conditional statements!

Jenn, Founder Calcworkshop ® , 15+ Years Experience (Licensed & Certified Teacher)

We’re going to walk through several examples to ensure you know what you’re doing.

In addition, this lesson will prepare you for deductive reasoning and two column proofs later on.

Here we go!

What are Conditional Statements?

To better understand deductive reasoning, we must first learn about conditional statements.

A conditional statement has two parts: hypothesis ( if ) and conclusion ( then ).

In fact, conditional statements are nothing more than “If-Then” statements!

Sometimes a picture helps form our hypothesis or conclusion. Therefore, we sometimes use Venn Diagrams to visually represent our findings and aid us in creating conditional statements.

But to verify statements are correct, we take a deeper look at our if-then statements. This is why we form the converse , inverse , and contrapositive of our conditional statements.

What is the Converse of a Statement?

Well, the converse is when we switch or interchange our hypothesis and conclusion.

Conditional Statement : “If today is Wednesday, then yesterday was Tuesday.”

Hypothesis : “If today is Wednesday” so our conclusion must follow “Then yesterday was Tuesday.”

So the converse is found by rearranging the hypothesis and conclusion, as Math Planet accurately states.

Converse : “If yesterday was Tuesday, then today is Wednesday.”

What is the Inverse of a Statement?

Now the inverse of an If-Then statement is found by negating (making negative) both the hypothesis and conclusion of the conditional statement.

So using our current conditional statement, “If today is Wednesday, then yesterday was Tuesday”.

Inverse : “If today is not Wednesday, then yesterday was not Tuesday.”

What is a Contrapositive?

And the contrapositive is formed by interchanging the hypothesis and conclusion and then negating both.

Contrapositive : “If yesterday was not Tuesday, then today is not Wednesday”

What is a Biconditional Statement?

A statement written in “if and only if” form combines a reversible statement and its true converse. In other words the conditional statement and converse are both true.

Continuing with our initial condition, “If today is Wednesday, then yesterday was Tuesday.”

Biconditional : “Today is Wednesday if and only if yesterday was Tuesday.”

Examples of Conditional Statements

In the video below we will look at several harder examples of how to form a proper statement, converse, inverse, and contrapositive. And here’s a big hint…

Whenever you see “con” that means you switch! It’s like being a con-artist!

Moreover, we will detail the process for coming up with reasons for our conclusions using known postulates. We will review the ten postulates that we have learned so far, and add a few more problems dealing with perpendicular lines, planes, and perpendicular bisectors.

After this lesson, we will be ready to tackle deductive reasoning head-on, and feel confident as we march onward toward learning two-column proofs!

Conditional Statements – Lesson & Examples (Video)

• Introduction to conditional statements
• 00:00:25 – What are conditional statements, converses, and biconditional statements? (Examples #1-2)
• 00:05:21 – Understanding venn diagrams (Examples #3-4)
• 00:11:07 – Supply the missing venn diagram and conditional statement for each question (Examples #5-8)
• Exclusive Content for Member’s Only
• 00:17:48 – Write the statement and converse then determine if they are reversible (Examples #9-12)
• 00:29:17 – Understanding the inverse, contrapositive, and symbol notation
• 00:35:33 – Write the statement, converse, inverse, contrapositive, and biconditional statements for each question (Examples #13-14)
• 00:45:40 – Using geometry postulates to verify statements (Example #15)
• 00:53:23 – What are perpendicular lines, perpendicular planes and the perpendicular bisector?
• 00:56:26 – Using the figure, determine if the statement is true or false (Example #16)
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you? Take a Tour and find out how a membership can take the struggle out of learning math.

Conditional Statement

A conditional statement is a part of mathematical reasoning which is a critical skill that enables students to analyze a given hypothesis without any reference to a particular context or meaning. In layman words, when a scientific inquiry or statement is examined, the reasoning is not based on an individual's opinion. Derivations and proofs need a factual and scientific basis. 

Mathematical critical thinking and logical reasoning are important skills that are required to solve maths reasoning questions.

In this mini-lesson, we will explore the world of conditional statements. We will walk through the answers to the questions like what is meant by a conditional statement, what are the parts of a conditional statement, and how to create conditional statements along with solved examples and interactive questions.

Lesson Plan  

What is meant by a conditional statement.

A statement that is of the form "If p, then q" is a conditional statement. Here 'p' refers to 'hypothesis' and 'q' refers to 'conclusion'.

For example, "If Cliff is thirsty, then she drinks water."

This is a conditional statement. It is also called an implication.

'\(\rightarrow\)' is the symbol used to represent the relation between two statements. For example, A\(\rightarrow\)B. It is known as the logical connector. It can be read as A implies B. 

Here are two more conditional statement examples

Example 1: If a number is divisible by 4, then it is divisible by 2.

Example 2: If today is Monday, then yesterday was Sunday.

What Are the Parts of a Conditional Statement?

Hypothesis (if) and Conclusion (then) are the two main parts that form a conditional statement.

Let us consider the above-stated example to understand the parts of a conditional statement.

Conditional Statement : If today is Monday, then yesterday was Sunday.

Hypothesis : "If today is Monday."

Conclusion : "Then yesterday was Sunday."

On interchanging the form of statement the relationship gets changed.

To check whether the statement is true or false here, we have subsequent parts of a conditional statement. They are:

• Contrapositive

Biconditional Statement

Let us consider hypothesis as statement A and Conclusion as statement B.

Following are the observations made:

Converse of Statement

When hypothesis and conclusion are switched or interchanged, it is termed as converse statement . For example,

Conditional Statement : “If today is Monday, then yesterday was Sunday.”

Hypothesis : “If today is Monday”

Converse : “If yesterday was Sunday, then today is Monday.”

Here the conditional statement logic is, If B, then A (B → A)

Inverse of Statement

When both the hypothesis and conclusion of the conditional statement are negative, it is termed as an inverse of the statement. For example,

Conditional Statement: “If today is Monday, then yesterday was Sunday”.

Inverse : “If today is not Monday, then yesterday was not Sunday.”

Here the conditional statement logic is, If not A, then not B (~A → ~B)

Contrapositive Statement

When the hypothesis and conclusion are negative and simultaneously interchanged, then the statement is contrapositive. For example,

Contrapositive: “If yesterday was not Sunday, then today is not Monday”

Here the conditional statement logic is, if not B, then not A (~B → ~A)

The statement is a biconditional statement when a statement satisfies both the conditions as true, being conditional and converse at the same time. For example,

Biconditional : “Today is Monday if and only if yesterday was Sunday.”

Here the conditional statement logic is, A if and only if B (A ↔ B)

How to Create Conditional Statements?

Here, the point to be kept in mind is that the 'If' and 'then' part must be true.

If a number is a perfect square , then it is even.

• 'If' part is a number that is a perfect square.

Think of 4 which is a perfect square.

This has become true.

• The 'then' part is that the number should be even. 4 is even.

This has also become true. 

Thus, we have set up a conditional statement.

Let us hypothetically consider two statements, statement A and statement B. Observe the truth table for the statements:

According to the table, only if the hypothesis (A) is true and the conclusion (B) is false then, A → B will be false, or else A → B will be true for all other conditions.

• A sentence needs to be either true or false, but not both, to be considered as a mathematically accepted statement.
• Any sentence which is either imperative or interrogative or exclamatory cannot be considered a mathematically validated statement. 
• A sentence containing one or many variables is termed as an open statement. An open statement can become a statement if the variables present in the sentence are replaced by definite values.

Solved Examples

Let us have a look at a few solved examples on conditional statements.

Identify the types of conditional statements.

There are four types of conditional statements:

• If condition
• If-else condition
• Nested if-else
• If-else ladder.

Ray tells "If the perimeter of a rectangle is 14, then its area is 10."

Which of the following could be the counterexamples? Justify your decision.

a) A rectangle with sides measuring 2 and 5

b) A rectangle with sides measuring 10 and 1

c) A rectangle with sides measuring 1 and 5

d) A rectangle with sides measuring 4 and 3

a) Rectangle with sides 2 and 5: Perimeter = 14 and area = 10

Both 'if' and 'then' are true.

b) Rectangle with sides 10 and 1: Perimeter = 22 and area = 10

'If' is false and 'then' is true.

c) Rectangle with sides 1 and 5: Perimeter = 12 and area = 5

Both 'if' and 'then' are false.

d) Rectangle with sides 4 and 3: Perimeter = 14 and area = 12

'If' is true and 'then' is false.

Joe examined the set of numbers {16, 27, 24} to check if they are the multiples of 3. He claimed that they are divisible by 9. Do you agree or disagree? Justify your answer.

Conditional statement : If a number is a multiple of 3, then it is divisible by 9.

Let us find whether the conditions are true or false.

a) 16 is not a multiple of 3. Thus, the condition is false. 

16 is not divisible by 9. Thus, the conclusion is false. 

b) 27 is a multiple of 3. Thus, the condition is true.

27 is divisible by 9. Thus, the conclusion is true. 

c) 24 is a multiple of 3. Thus the condition is true.

24 is not divisible by 9. Thus the conclusion is false.

Write the converse, inverse, and contrapositive statement for the following conditional statement. 

If you study well, then you will pass the exam.

The given statement is - If you study well, then you will pass the exam.

It is of the form, "If p, then q"

The converse statement is, "You will pass the exam if you study well" (if q, then p).

The inverse statement is, "If you do not study well then you will not pass the exam" (if not p, then not q).

The contrapositive statement is, "If you did not pass the exam, then you did not study well" (if not q, then not p).

Interactive Questions

Here are a few activities for you to practice. Select/Type your answer and click the "Check Answer" button to see the result.

Let's Summarize

The mini-lesson targeted the fascinating concept of the conditional statement. The math journey around conditional statements started with what a student already knew and went on to creatively crafting a fresh concept in the young minds. Done in a way that not only it is relatable and easy to grasp, but also will stay with them forever.

About Cuemath

At  Cuemath , our team of math experts is dedicated to making learning fun for our favorite readers, the students!

Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.

Be it worksheets, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we, at Cuemath, believe in.

FAQs on Conditional Statement

1. what is the most common conditional statement.

'If and then' is the most commonly used conditional statement.

2. When do you use a conditional statement?

Conditional statements are used to justify the given condition or two statements as true or false.

3. What is if and if-else statement?

If is used when a specified condition is true. If-else is used when a particular specified condition is not satisfying and is false.

4. What is the symbol for a conditional statement?

'\(\rightarrow\)' is the symbol used to represent the relation between two statements. For example, A\(\rightarrow\)B. It is known as the logical connector. It can be read as A implies B.

5. What is the Contrapositive of a conditional statement?

If not B, then not A (~B → ~A)

6. What is a universal conditional statement?

Conditional statements are those statements where a hypothesis is followed by a conclusion. It is also known as an " If-then" statement. If the hypothesis is true and the conclusion is false, then the conditional statement is false. Likewise, if the hypothesis is false the whole statement is false. Conditional statements are also termed as implications.

Conditional Statement: If today is Monday, then yesterday was Sunday

Hypothesis: "If today is Monday."

Conclusion: "Then yesterday was Sunday."

If A, then B (A → B)

• Live one on one classroom and doubt clearing
• Practice worksheets in and after class for conceptual clarity
• Personalized curriculum to keep up with school

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 31289

CO-6: Apply basic concepts of probability, random variation, and commonly used statistical probability distributions.

Learning Objectives

LO 6.26: Outline the logic and process of hypothesis testing.

LO 6.27: Explain what the p-value is and how it is used to draw conclusions.

Video: Hypothesis Testing (8:43)

Introduction

We are in the middle of the part of the course that has to do with inference for one variable.

So far, we talked about point estimation and learned how interval estimation enhances it by quantifying the magnitude of the estimation error (with a certain level of confidence) in the form of the margin of error. The result is the confidence interval — an interval that, with a certain confidence, we believe captures the unknown parameter.

We are now moving to the other kind of inference, hypothesis testing . We say that hypothesis testing is “the other kind” because, unlike the inferential methods we presented so far, where the goal was estimating the unknown parameter, the idea, logic and goal of hypothesis testing are quite different.

In the first two parts of this section we will discuss the idea behind hypothesis testing, explain how it works, and introduce new terminology that emerges in this form of inference. The final two parts will be more specific and will discuss hypothesis testing for the population proportion ( p ) and the population mean ( μ, mu).

If this is your first statistics course, you will need to spend considerable time on this topic as there are many new ideas. Many students find this process and its logic difficult to understand in the beginning.

In this section, we will use the hypothesis test for a population proportion to motivate our understanding of the process. We will conduct these tests manually. For all future hypothesis test procedures, including problems involving means, we will use software to obtain the results and focus on interpreting them in the context of our scenario.

General Idea and Logic of Hypothesis Testing

The purpose of this section is to gradually build your understanding about how statistical hypothesis testing works. We start by explaining the general logic behind the process of hypothesis testing. Once we are confident that you understand this logic, we will add some more details and terminology.

To start our discussion about the idea behind statistical hypothesis testing, consider the following example:

A case of suspected cheating on an exam is brought in front of the disciplinary committee at a certain university.

There are two opposing claims in this case:

• The student’s claim: I did not cheat on the exam.
• The instructor’s claim: The student did cheat on the exam.

Adhering to the principle “innocent until proven guilty,” the committee asks the instructor for evidence to support his claim. The instructor explains that the exam had two versions, and shows the committee members that on three separate exam questions, the student used in his solution numbers that were given in the other version of the exam.

The committee members all agree that it would be extremely unlikely to get evidence like that if the student’s claim of not cheating had been true. In other words, the committee members all agree that the instructor brought forward strong enough evidence to reject the student’s claim, and conclude that the student did cheat on the exam.

What does this example have to do with statistics?

While it is true that this story seems unrelated to statistics, it captures all the elements of hypothesis testing and the logic behind it. Before you read on to understand why, it would be useful to read the example again. Please do so now.

Statistical hypothesis testing is defined as:

• Assessing evidence provided by the data against the null claim (the claim which is to be assumed true unless enough evidence exists to reject it).

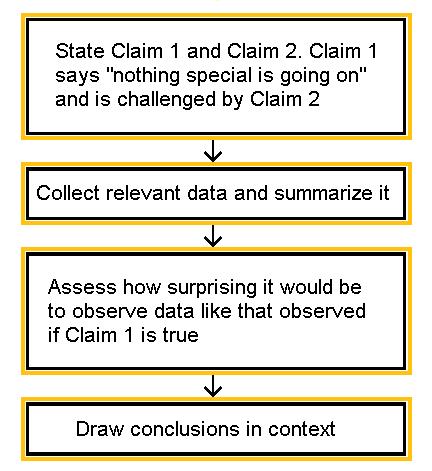
Here is how the process of statistical hypothesis testing works:

• We have two claims about what is going on in the population. Let’s call them claim 1 (this will be the null claim or hypothesis) and claim 2 (this will be the alternative) . Much like the story above, where the student’s claim is challenged by the instructor’s claim, the null claim 1 is challenged by the alternative claim 2. (For us, these claims are usually about the value of population parameter(s) or about the existence or nonexistence of a relationship between two variables in the population).
• We choose a sample, collect relevant data and summarize them (this is similar to the instructor collecting evidence from the student’s exam). For statistical tests, this step will also involve checking any conditions or assumptions.
• We figure out how likely it is to observe data like the data we obtained, if claim 1 is true. (Note that the wording “how likely …” implies that this step requires some kind of probability calculation). In the story, the committee members assessed how likely it is to observe evidence such as the instructor provided, had the student’s claim of not cheating been true.
• If, after assuming claim 1 is true, we find that it would be extremely unlikely to observe data as strong as ours or stronger in favor of claim 2, then we have strong evidence against claim 1, and we reject it in favor of claim 2. Later we will see this corresponds to a small p-value.
• If, after assuming claim 1 is true, we find that observing data as strong as ours or stronger in favor of claim 2 is NOT VERY UNLIKELY , then we do not have enough evidence against claim 1, and therefore we cannot reject it in favor of claim 2. Later we will see this corresponds to a p-value which is not small.

In our story, the committee decided that it would be extremely unlikely to find the evidence that the instructor provided had the student’s claim of not cheating been true. In other words, the members felt that it is extremely unlikely that it is just a coincidence (random chance) that the student used the numbers from the other version of the exam on three separate problems. The committee members therefore decided to reject the student’s claim and concluded that the student had, indeed, cheated on the exam. (Wouldn’t you conclude the same?)

Hopefully this example helped you understand the logic behind hypothesis testing.

Interactive Applet: Reasoning of a Statistical Test

To strengthen your understanding of the process of hypothesis testing and the logic behind it, let’s look at three statistical examples.

A recent study estimated that 20% of all college students in the United States smoke. The head of Health Services at Goodheart University (GU) suspects that the proportion of smokers may be lower at GU. In hopes of confirming her claim, the head of Health Services chooses a random sample of 400 Goodheart students, and finds that 70 of them are smokers.

Let’s analyze this example using the 4 steps outlined above:

• claim 1: The proportion of smokers at Goodheart is 0.20.
• claim 2: The proportion of smokers at Goodheart is less than 0.20.

Claim 1 basically says “nothing special goes on at Goodheart University; the proportion of smokers there is no different from the proportion in the entire country.” This claim is challenged by the head of Health Services, who suspects that the proportion of smokers at Goodheart is lower.

• Choosing a sample and collecting data: A sample of n = 400 was chosen, and summarizing the data revealed that the sample proportion of smokers is p -hat = 70/400 = 0.175.While it is true that 0.175 is less than 0.20, it is not clear whether this is strong enough evidence against claim 1. We must account for sampling variation.
• Assessment of evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves: How surprising is it to get a sample proportion as low as p -hat = 0.175 (or lower), assuming claim 1 is true? In other words, we need to find how likely it is that in a random sample of size n = 400 taken from a population where the proportion of smokers is p = 0.20 we’ll get a sample proportion as low as p -hat = 0.175 (or lower).It turns out that the probability that we’ll get a sample proportion as low as p -hat = 0.175 (or lower) in such a sample is roughly 0.106 (do not worry about how this was calculated at this point – however, if you think about it hopefully you can see that the key is the sampling distribution of p -hat).
• Conclusion: Well, we found that if claim 1 were true there is a probability of 0.106 of observing data like that observed or more extreme. Now you have to decide …Do you think that a probability of 0.106 makes our data rare enough (surprising enough) under claim 1 so that the fact that we did observe it is enough evidence to reject claim 1? Or do you feel that a probability of 0.106 means that data like we observed are not very likely when claim 1 is true, but they are not unlikely enough to conclude that getting such data is sufficient evidence to reject claim 1. Basically, this is your decision. However, it would be nice to have some kind of guideline about what is generally considered surprising enough.

A certain prescription allergy medicine is supposed to contain an average of 245 parts per million (ppm) of a certain chemical. If the concentration is higher than 245 ppm, the drug will likely cause unpleasant side effects, and if the concentration is below 245 ppm, the drug may be ineffective. The manufacturer wants to check whether the mean concentration in a large shipment is the required 245 ppm or not. To this end, a random sample of 64 portions from the large shipment is tested, and it is found that the sample mean concentration is 250 ppm with a sample standard deviation of 12 ppm.

• Claim 1: The mean concentration in the shipment is the required 245 ppm.
• Claim 2: The mean concentration in the shipment is not the required 245 ppm.

Note that again, claim 1 basically says: “There is nothing unusual about this shipment, the mean concentration is the required 245 ppm.” This claim is challenged by the manufacturer, who wants to check whether that is, indeed, the case or not.

• Choosing a sample and collecting data: A sample of n = 64 portions is chosen and after summarizing the data it is found that the sample mean concentration is x-bar = 250 and the sample standard deviation is s = 12.Is the fact that x-bar = 250 is different from 245 strong enough evidence to reject claim 1 and conclude that the mean concentration in the whole shipment is not the required 245? In other words, do the data provide strong enough evidence to reject claim 1?
• Assessing the evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves the following question: If the mean concentration in the whole shipment were really the required 245 ppm (i.e., if claim 1 were true), how surprising would it be to observe a sample of 64 portions where the sample mean concentration is off by 5 ppm or more (as we did)? It turns out that it would be extremely unlikely to get such a result if the mean concentration were really the required 245. There is only a probability of 0.0007 (i.e., 7 in 10,000) of that happening. (Do not worry about how this was calculated at this point, but again, the key will be the sampling distribution.)
• Making conclusions: Here, it is pretty clear that a sample like the one we observed or more extreme is VERY rare (or extremely unlikely) if the mean concentration in the shipment were really the required 245 ppm. The fact that we did observe such a sample therefore provides strong evidence against claim 1, so we reject it and conclude with very little doubt that the mean concentration in the shipment is not the required 245 ppm.

Do you think that you’re getting it? Let’s make sure, and look at another example.

Is there a relationship between gender and combined scores (Math + Verbal) on the SAT exam?

Following a report on the College Board website, which showed that in 2003, males scored generally higher than females on the SAT exam, an educational researcher wanted to check whether this was also the case in her school district. The researcher chose random samples of 150 males and 150 females from her school district, collected data on their SAT performance and found the following:

Again, let’s see how the process of hypothesis testing works for this example:

• Claim 1: Performance on the SAT is not related to gender (males and females score the same).
• Claim 2: Performance on the SAT is related to gender – males score higher.

Note that again, claim 1 basically says: “There is nothing going on between the variables SAT and gender.” Claim 2 represents what the researcher wants to check, or suspects might actually be the case.

• Choosing a sample and collecting data: Data were collected and summarized as given above. Is the fact that the sample mean score of males (1,025) is higher than the sample mean score of females (1,010) by 15 points strong enough information to reject claim 1 and conclude that in this researcher’s school district, males score higher on the SAT than females?
• Assessment of evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves: If SAT scores are in fact not related to gender (claim 1 is true), how likely is it to get data like the data we observed, in which the difference between the males’ average and females’ average score is as high as 15 points or higher? It turns out that the probability of observing such a sample result if SAT score is not related to gender is approximately 0.29 (Again, do not worry about how this was calculated at this point).
• Conclusion: Here, we have an example where observing a sample like the one we observed or more extreme is definitely not surprising (roughly 30% chance) if claim 1 were true (i.e., if indeed there is no difference in SAT scores between males and females). We therefore conclude that our data does not provide enough evidence for rejecting claim 1.
• “The data provide enough evidence to reject claim 1 and accept claim 2”; or
• “The data do not provide enough evidence to reject claim 1.”

In particular, note that in the second type of conclusion we did not say: “ I accept claim 1 ,” but only “ I don’t have enough evidence to reject claim 1 .” We will come back to this issue later, but this is a good place to make you aware of this subtle difference.

Hopefully by now, you understand the logic behind the statistical hypothesis testing process. Here is a summary:

Learn by Doing: Logic of Hypothesis Testing

Did I Get This?: Logic of Hypothesis Testing

Steps in Hypothesis Testing

Video: Steps in Hypothesis Testing (16:02)

Now that we understand the general idea of how statistical hypothesis testing works, let’s go back to each of the steps and delve slightly deeper, getting more details and learning some terminology.

Hypothesis Testing Step 1: State the Hypotheses

In all three examples, our aim is to decide between two opposing points of view, Claim 1 and Claim 2. In hypothesis testing, Claim 1 is called the null hypothesis (denoted “ Ho “), and Claim 2 plays the role of the alternative hypothesis (denoted “ Ha “). As we saw in the three examples, the null hypothesis suggests nothing special is going on; in other words, there is no change from the status quo, no difference from the traditional state of affairs, no relationship. In contrast, the alternative hypothesis disagrees with this, stating that something is going on, or there is a change from the status quo, or there is a difference from the traditional state of affairs. The alternative hypothesis, Ha, usually represents what we want to check or what we suspect is really going on.

Let’s go back to our three examples and apply the new notation:

In example 1:

• Ho: The proportion of smokers at GU is 0.20.
• Ha: The proportion of smokers at GU is less than 0.20.

In example 2:

• Ho: The mean concentration in the shipment is the required 245 ppm.
• Ha: The mean concentration in the shipment is not the required 245 ppm.

In example 3:

• Ho: Performance on the SAT is not related to gender (males and females score the same).
• Ha: Performance on the SAT is related to gender – males score higher.

Learn by Doing: State the Hypotheses

Did I Get This?: State the Hypotheses

Hypothesis Testing Step 2: Collect Data, Check Conditions and Summarize Data

This step is pretty obvious. This is what inference is all about. You look at sampled data in order to draw conclusions about the entire population. In the case of hypothesis testing, based on the data, you draw conclusions about whether or not there is enough evidence to reject Ho.

There is, however, one detail that we would like to add here. In this step we collect data and summarize it. Go back and look at the second step in our three examples. Note that in order to summarize the data we used simple sample statistics such as the sample proportion ( p -hat), sample mean (x-bar) and the sample standard deviation (s).

In practice, you go a step further and use these sample statistics to summarize the data with what’s called a test statistic . We are not going to go into any details right now, but we will discuss test statistics when we go through the specific tests.

This step will also involve checking any conditions or assumptions required to use the test.

Hypothesis Testing Step 3: Assess the Evidence

As we saw, this is the step where we calculate how likely is it to get data like that observed (or more extreme) when Ho is true. In a sense, this is the heart of the process, since we draw our conclusions based on this probability.

• If this probability is very small (see example 2), then that means that it would be very surprising to get data like that observed (or more extreme) if Ho were true. The fact that we did observe such data is therefore evidence against Ho, and we should reject it.
• On the other hand, if this probability is not very small (see example 3) this means that observing data like that observed (or more extreme) is not very surprising if Ho were true. The fact that we observed such data does not provide evidence against Ho. This crucial probability, therefore, has a special name. It is called the p-value of the test.

In our three examples, the p-values were given to you (and you were reassured that you didn’t need to worry about how these were derived yet):

• Example 1: p-value = 0.106
• Example 2: p-value = 0.0007
• Example 3: p-value = 0.29

Obviously, the smaller the p-value, the more surprising it is to get data like ours (or more extreme) when Ho is true, and therefore, the stronger the evidence the data provide against Ho.

Looking at the three p-values of our three examples, we see that the data that we observed in example 2 provide the strongest evidence against the null hypothesis, followed by example 1, while the data in example 3 provides the least evidence against Ho.

• Right now we will not go into specific details about p-value calculations, but just mention that since the p-value is the probability of getting data like those observed (or more extreme) when Ho is true, it would make sense that the calculation of the p-value will be based on the data summary, which, as we mentioned, is the test statistic. Indeed, this is the case. In practice, we will mostly use software to provide the p-value for us.

Hypothesis Testing Step 4: Making Conclusions

Since our statistical conclusion is based on how small the p-value is, or in other words, how surprising our data are when Ho is true, it would be nice to have some kind of guideline or cutoff that will help determine how small the p-value must be, or how “rare” (unlikely) our data must be when Ho is true, for us to conclude that we have enough evidence to reject Ho.

This cutoff exists, and because it is so important, it has a special name. It is called the significance level of the test and is usually denoted by the Greek letter α (alpha). The most commonly used significance level is α (alpha) = 0.05 (or 5%). This means that:

• if the p-value < α (alpha) (usually 0.05), then the data we obtained is considered to be “rare (or surprising) enough” under the assumption that Ho is true, and we say that the data provide statistically significant evidence against Ho, so we reject Ho and thus accept Ha.
• if the p-value > α (alpha)(usually 0.05), then our data are not considered to be “surprising enough” under the assumption that Ho is true, and we say that our data do not provide enough evidence to reject Ho (or, equivalently, that the data do not provide enough evidence to accept Ha).

Now that we have a cutoff to use, here are the appropriate conclusions for each of our examples based upon the p-values we were given.

In Example 1:

• Using our cutoff of 0.05, we fail to reject Ho.
• Conclusion : There IS NOT enough evidence that the proportion of smokers at GU is less than 0.20
• Still we should consider: Does the evidence seen in the data provide any practical evidence towards our alternative hypothesis?

In Example 2:

• Using our cutoff of 0.05, we reject Ho.
• Conclusion : There IS enough evidence that the mean concentration in the shipment is not the required 245 ppm.

In Example 3:

• Conclusion : There IS NOT enough evidence that males score higher on average than females on the SAT.

Notice that all of the above conclusions are written in terms of the alternative hypothesis and are given in the context of the situation. In no situation have we claimed the null hypothesis is true. Be very careful of this and other issues discussed in the following comments.

• Although the significance level provides a good guideline for drawing our conclusions, it should not be treated as an incontrovertible truth. There is a lot of room for personal interpretation. What if your p-value is 0.052? You might want to stick to the rules and say “0.052 > 0.05 and therefore I don’t have enough evidence to reject Ho”, but you might decide that 0.052 is small enough for you to believe that Ho should be rejected. It should be noted that scientific journals do consider 0.05 to be the cutoff point for which any p-value below the cutoff indicates enough evidence against Ho, and any p-value above it, or even equal to it , indicates there is not enough evidence against Ho. Although a p-value between 0.05 and 0.10 is often reported as marginally statistically significant.
• It is important to draw your conclusions in context . It is never enough to say: “p-value = …, and therefore I have enough evidence to reject Ho at the 0.05 significance level.” You should always word your conclusion in terms of the data. Although we will use the terminology of “rejecting Ho” or “failing to reject Ho” – this is mostly due to the fact that we are instructing you in these concepts. In practice, this language is rarely used. We also suggest writing your conclusion in terms of the alternative hypothesis.Is there or is there not enough evidence that the alternative hypothesis is true?
• Let’s go back to the issue of the nature of the two types of conclusions that I can make.
• Either I reject Ho (when the p-value is smaller than the significance level)
• or I cannot reject Ho (when the p-value is larger than the significance level).

As we mentioned earlier, note that the second conclusion does not imply that I accept Ho, but just that I don’t have enough evidence to reject it. Saying (by mistake) “I don’t have enough evidence to reject Ho so I accept it” indicates that the data provide evidence that Ho is true, which is not necessarily the case . Consider the following slightly artificial yet effective example:

An employer claims to subscribe to an “equal opportunity” policy, not hiring men any more often than women for managerial positions. Is this credible? You’re not sure, so you want to test the following two hypotheses:

• Ho: The proportion of male managers hired is 0.5
• Ha: The proportion of male managers hired is more than 0.5

Data: You choose at random three of the new managers who were hired in the last 5 years and find that all 3 are men.

Assessing Evidence: If the proportion of male managers hired is really 0.5 (Ho is true), then the probability that the random selection of three managers will yield three males is therefore 0.5 * 0.5 * 0.5 = 0.125. This is the p-value (using the multiplication rule for independent events).

Conclusion: Using 0.05 as the significance level, you conclude that since the p-value = 0.125 > 0.05, the fact that the three randomly selected managers were all males is not enough evidence to reject the employer’s claim of subscribing to an equal opportunity policy (Ho).

However, the data (all three selected are males) definitely does NOT provide evidence to accept the employer’s claim (Ho).

Learn By Doing: Using p-values

Did I Get This?: Using p-values

Comment about wording: Another common wording in scientific journals is:

• “The results are statistically significant” – when the p-value < α (alpha).
• “The results are not statistically significant” – when the p-value > α (alpha).

Often you will see significance levels reported with additional description to indicate the degree of statistical significance. A general guideline (although not required in our course) is:

• If 0.01 ≤ p-value < 0.05, then the results are (statistically) significant .
• If 0.001 ≤ p-value < 0.01, then the results are highly statistically significant .
• If p-value < 0.001, then the results are very highly statistically significant .
• If p-value > 0.05, then the results are not statistically significant (NS).
• If 0.05 ≤ p-value < 0.10, then the results are marginally statistically significant .

Let’s summarize

We learned quite a lot about hypothesis testing. We learned the logic behind it, what the key elements are, and what types of conclusions we can and cannot draw in hypothesis testing. Here is a quick recap:

Video: Hypothesis Testing Overview (2:20)

Here are a few more activities if you need some additional practice.

Did I Get This?: Hypothesis Testing Overview

• Notice that the p-value is an example of a conditional probability . We calculate the probability of obtaining results like those of our data (or more extreme) GIVEN the null hypothesis is true. We could write P(Obtaining results like ours or more extreme | Ho is True).
• We could write P(Obtaining a test statistic as or more extreme than ours | Ho is True).
• In this case we are asking “Assuming the null hypothesis is true, how rare is it to observe something as or more extreme than what I have found in my data?”
• If after assuming the null hypothesis is true, what we have found in our data is extremely rare (small p-value), this provides evidence to reject our assumption that Ho is true in favor of Ha.
• The p-value can also be thought of as the probability, assuming the null hypothesis is true, that the result we have seen is solely due to random error (or random chance). We have already seen that statistics from samples collected from a population vary. There is random error or random chance involved when we sample from populations.

In this setting, if the p-value is very small, this implies, assuming the null hypothesis is true, that it is extremely unlikely that the results we have obtained would have happened due to random error alone, and thus our assumption (Ho) is rejected in favor of the alternative hypothesis (Ha).

• It is EXTREMELY important that you find a definition of the p-value which makes sense to you. New students often need to contemplate this idea repeatedly through a variety of examples and explanations before becoming comfortable with this idea. It is one of the two most important concepts in statistics (the other being confidence intervals).
• We infer that the alternative hypothesis is true ONLY by rejecting the null hypothesis.
• A statistically significant result is one that has a very low probability of occurring if the null hypothesis is true.
• Results which are statistically significant may or may not have practical significance and vice versa.

Error and Power

LO 6.28: Define a Type I and Type II error in general and in the context of specific scenarios.

LO 6.29: Explain the concept of the power of a statistical test including the relationship between power, sample size, and effect size.

Video: Errors and Power (12:03)

Type I and Type II Errors in Hypothesis Tests

We have not yet discussed the fact that we are not guaranteed to make the correct decision by this process of hypothesis testing. Maybe you are beginning to see that there is always some level of uncertainty in statistics.

Let’s think about what we know already and define the possible errors we can make in hypothesis testing. When we conduct a hypothesis test, we choose one of two possible conclusions based upon our data.

If the p-value is smaller than your pre-specified significance level (α, alpha), you reject the null hypothesis and either

• You have made the correct decision since the null hypothesis is false
• You have made an error ( Type I ) and rejected Ho when in fact Ho is true (your data happened to be a RARE EVENT under Ho)

If the p-value is greater than (or equal to) your chosen significance level (α, alpha), you fail to reject the null hypothesis and either

• You have made the correct decision since the null hypothesis is true
• You have made an error ( Type II ) and failed to reject Ho when in fact Ho is false (the alternative hypothesis, Ha, is true)

The following summarizes the four possible results which can be obtained from a hypothesis test. Notice the rows represent the decision made in the hypothesis test and the columns represent the (usually unknown) truth in reality.

Although the truth is unknown in practice – or we would not be conducting the test – we know it must be the case that either the null hypothesis is true or the null hypothesis is false. It is also the case that either decision we make in a hypothesis test can result in an incorrect conclusion!

A TYPE I Error occurs when we Reject Ho when, in fact, Ho is True. In this case, we mistakenly reject a true null hypothesis.

• P(TYPE I Error) = P(Reject Ho | Ho is True) = α = alpha = Significance Level

A TYPE II Error occurs when we fail to Reject Ho when, in fact, Ho is False. In this case we fail to reject a false null hypothesis.

P(TYPE II Error) = P(Fail to Reject Ho | Ho is False) = β = beta

When our significance level is 5%, we are saying that we will allow ourselves to make a Type I error less than 5% of the time. In the long run, if we repeat the process, 5% of the time we will find a p-value < 0.05 when in fact the null hypothesis was true.

In this case, our data represent a rare occurrence which is unlikely to happen but is still possible. For example, suppose we toss a coin 10 times and obtain 10 heads, this is unlikely for a fair coin but not impossible. We might conclude the coin is unfair when in fact we simply saw a very rare event for this fair coin.

Our testing procedure CONTROLS for the Type I error when we set a pre-determined value for the significance level.

Notice that these probabilities are conditional probabilities. This is one more reason why conditional probability is an important concept in statistics.

Unfortunately, calculating the probability of a Type II error requires us to know the truth about the population. In practice we can only calculate this probability using a series of “what if” calculations which depend upon the type of problem.

Comment: As you initially read through the examples below, focus on the broad concepts instead of the small details. It is not important to understand how to calculate these values yourself at this point.

• Try to understand the pictures we present. Which pictures represent an assumed null hypothesis and which represent an alternative?
• It may be useful to come back to this page (and the activities here) after you have reviewed the rest of the section on hypothesis testing and have worked a few problems yourself.

Interactive Applet: Statistical Significance

Here are two examples of using an older version of this applet. It looks slightly different but the same settings and options are available in the version above.

In both cases we will consider IQ scores.

Our null hypothesis is that the true mean is 100. Assume the standard deviation is 16 and we will specify a significance level of 5%.

In this example we will specify that the true mean is indeed 100 so that the null hypothesis is true. Most of the time (95%), when we generate a sample, we should fail to reject the null hypothesis since the null hypothesis is indeed true.

Here is one sample that results in a correct decision:

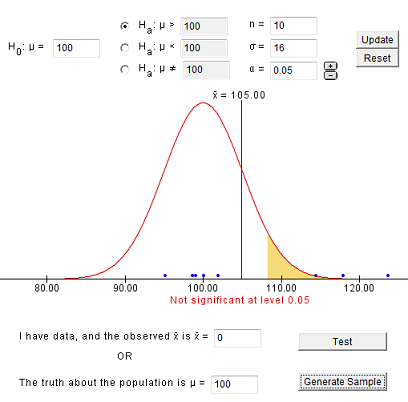
In the sample above, we obtain an x-bar of 105, which is drawn on the distribution which assumes μ (mu) = 100 (the null hypothesis is true). Notice the sample is shown as blue dots along the x-axis and the shaded region shows for which values of x-bar we would reject the null hypothesis. In other words, we would reject Ho whenever the x-bar falls in the shaded region.

Enter the same values and generate samples until you obtain a Type I error (you falsely reject the null hypothesis). You should see something like this:

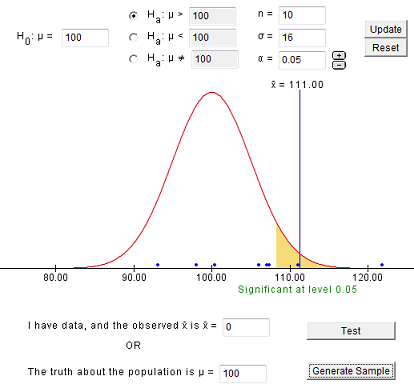
If you were to generate 100 samples, you should have around 5% where you rejected Ho. These would be samples which would result in a Type I error.

The previous example illustrates a correct decision and a Type I error when the null hypothesis is true. The next example illustrates a correct decision and Type II error when the null hypothesis is false. In this case, we must specify the true population mean.

Let’s suppose we are sampling from an honors program and that the true mean IQ for this population is 110. We do not know the probability of a Type II error without more detailed calculations.

Let’s start with a sample which results in a correct decision.

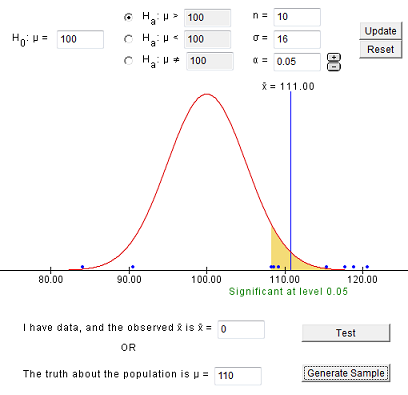
In the sample above, we obtain an x-bar of 111, which is drawn on the distribution which assumes μ (mu) = 100 (the null hypothesis is true).

Enter the same values and generate samples until you obtain a Type II error (you fail to reject the null hypothesis). You should see something like this:

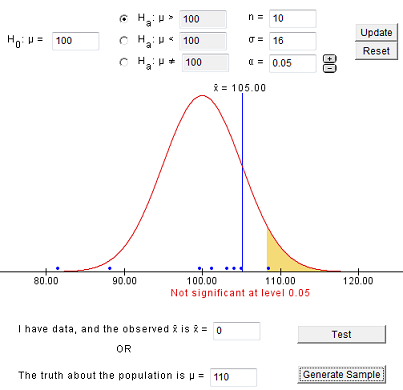
You should notice that in this case (when Ho is false), it is easier to obtain an incorrect decision (a Type II error) than it was in the case where Ho is true. If you generate 100 samples, you can approximate the probability of a Type II error.

We can find the probability of a Type II error by visualizing both the assumed distribution and the true distribution together. The image below is adapted from an applet we will use when we discuss the power of a statistical test.

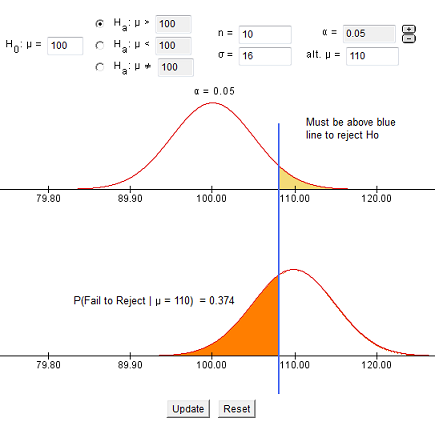
There is a 37.4% chance that, in the long run, we will make a Type II error and fail to reject the null hypothesis when in fact the true mean IQ is 110 in the population from which we sample our 10 individuals.

Can you visualize what will happen if the true population mean is really 115 or 108? When will the Type II error increase? When will it decrease? We will look at this idea again when we discuss the concept of power in hypothesis tests.

• It is important to note that there is a trade-off between the probability of a Type I and a Type II error. If we decrease the probability of one of these errors, the probability of the other will increase! The practical result of this is that if we require stronger evidence to reject the null hypothesis (smaller significance level = probability of a Type I error), we will increase the chance that we will be unable to reject the null hypothesis when in fact Ho is false (increases the probability of a Type II error).
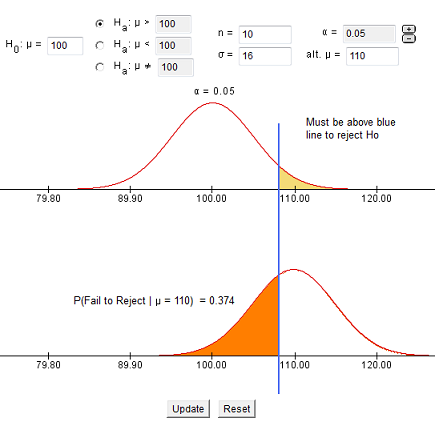
• When α (alpha) = 0.05 we obtained a Type II error probability of 0.374 = β = beta

• When α (alpha) = 0.01 (smaller than before) we obtain a Type II error probability of 0.644 = β = beta (larger than before)

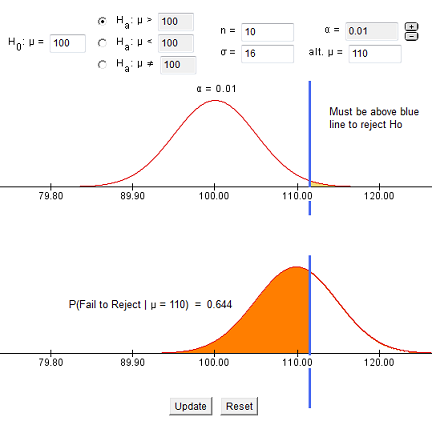
• As the blue line in the picture moves farther right, the significance level (α, alpha) is decreasing and the Type II error probability is increasing.
• As the blue line in the picture moves farther left, the significance level (α, alpha) is increasing and the Type II error probability is decreasing

Let’s return to our very first example and define these two errors in context.

• Ho = The student’s claim: I did not cheat on the exam.
• Ha = The instructor’s claim: The student did cheat on the exam.

Adhering to the principle “innocent until proven guilty,” the committee asks the instructor for evidence to support his claim.

There are four possible outcomes of this process. There are two possible correct decisions:

• The student did cheat on the exam and the instructor brings enough evidence to reject Ho and conclude the student did cheat on the exam. This is a CORRECT decision!
• The student did not cheat on the exam and the instructor fails to provide enough evidence that the student did cheat on the exam. This is a CORRECT decision!

Both the correct decisions and the possible errors are fairly easy to understand but with the errors, you must be careful to identify and define the two types correctly.

TYPE I Error: Reject Ho when Ho is True

• The student did not cheat on the exam but the instructor brings enough evidence to reject Ho and conclude the student cheated on the exam. This is a Type I Error.

TYPE II Error: Fail to Reject Ho when Ho is False

• The student did cheat on the exam but the instructor fails to provide enough evidence that the student cheated on the exam. This is a Type II Error.

In most situations, including this one, it is more “acceptable” to have a Type II error than a Type I error. Although allowing a student who cheats to go unpunished might be considered a very bad problem, punishing a student for something he or she did not do is usually considered to be a more severe error. This is one reason we control for our Type I error in the process of hypothesis testing.

Did I Get This?: Type I and Type II Errors (in context)

• The probabilities of Type I and Type II errors are closely related to the concepts of sensitivity and specificity that we discussed previously. Consider the following hypotheses:

Ho: The individual does not have diabetes (status quo, nothing special happening)

Ha: The individual does have diabetes (something is going on here)

In this setting:

When someone tests positive for diabetes we would reject the null hypothesis and conclude the person has diabetes (we may or may not be correct!).

When someone tests negative for diabetes we would fail to reject the null hypothesis so that we fail to conclude the person has diabetes (we may or may not be correct!)

Let’s take it one step further:

Sensitivity = P(Test + | Have Disease) which in this setting equals P(Reject Ho | Ho is False) = 1 – P(Fail to Reject Ho | Ho is False) = 1 – β = 1 – beta

Specificity = P(Test – | No Disease) which in this setting equals P(Fail to Reject Ho | Ho is True) = 1 – P(Reject Ho | Ho is True) = 1 – α = 1 – alpha

Notice that sensitivity and specificity relate to the probability of making a correct decision whereas α (alpha) and β (beta) relate to the probability of making an incorrect decision.

Usually α (alpha) = 0.05 so that the specificity listed above is 0.95 or 95%.

Next, we will see that the sensitivity listed above is the power of the hypothesis test!

Reasons for a Type I Error in Practice

Assuming that you have obtained a quality sample:

• The reason for a Type I error is random chance.
• When a Type I error occurs, our observed data represented a rare event which indicated evidence in favor of the alternative hypothesis even though the null hypothesis was actually true.

Reasons for a Type II Error in Practice

Again, assuming that you have obtained a quality sample, now we have a few possibilities depending upon the true difference that exists.

• The sample size is too small to detect an important difference. This is the worst case, you should have obtained a larger sample. In this situation, you may notice that the effect seen in the sample seems PRACTICALLY significant and yet the p-value is not small enough to reject the null hypothesis.
• The sample size is reasonable for the important difference but the true difference (which might be somewhat meaningful or interesting) is smaller than your test was capable of detecting. This is tolerable as you were not interested in being able to detect this difference when you began your study. In this situation, you may notice that the effect seen in the sample seems to have some potential for practical significance.
• The sample size is more than adequate, the difference that was not detected is meaningless in practice. This is not a problem at all and is in effect a “correct decision” since the difference you did not detect would have no practical meaning.
• Note: We will discuss the idea of practical significance later in more detail.

Power of a Hypothesis Test

It is often the case that we truly wish to prove the alternative hypothesis. It is reasonable that we would be interested in the probability of correctly rejecting the null hypothesis. In other words, the probability of rejecting the null hypothesis, when in fact the null hypothesis is false. This can also be thought of as the probability of being able to detect a (pre-specified) difference of interest to the researcher.

Let’s begin with a realistic example of how power can be described in a study.

In a clinical trial to study two medications for weight loss, we have an 80% chance to detect a difference in the weight loss between the two medications of 10 pounds. In other words, the power of the hypothesis test we will conduct is 80%.

In other words, if one medication comes from a population with an average weight loss of 25 pounds and the other comes from a population with an average weight loss of 15 pounds, we will have an 80% chance to detect that difference using the sample we have in our trial.

If we were to repeat this trial many times, 80% of the time we will be able to reject the null hypothesis (that there is no difference between the medications) and 20% of the time we will fail to reject the null hypothesis (and make a Type II error!).

The difference of 10 pounds in the previous example, is often called the effect size . The measure of the effect differs depending on the particular test you are conducting but is always some measure related to the true effect in the population. In this example, it is the difference between two population means.

Recall the definition of a Type II error:

Notice that P(Reject Ho | Ho is False) = 1 – P(Fail to Reject Ho | Ho is False) = 1 – β = 1- beta.

The POWER of a hypothesis test is the probability of rejecting the null hypothesis when the null hypothesis is false . This can also be stated as the probability of correctly rejecting the null hypothesis .

POWER = P(Reject Ho | Ho is False) = 1 – β = 1 – beta

Power is the test’s ability to correctly reject the null hypothesis. A test with high power has a good chance of being able to detect the difference of interest to us, if it exists .

As we mentioned on the bottom of the previous page, this can be thought of as the sensitivity of the hypothesis test if you imagine Ho = No disease and Ha = Disease.

Factors Affecting the Power of a Hypothesis Test

The power of a hypothesis test is affected by numerous quantities (similar to the margin of error in a confidence interval).

Assume that the null hypothesis is false for a given hypothesis test. All else being equal, we have the following:

• Larger samples result in a greater chance to reject the null hypothesis which means an increase in the power of the hypothesis test.
• If the effect size is larger, it will become easier for us to detect. This results in a greater chance to reject the null hypothesis which means an increase in the power of the hypothesis test. The effect size varies for each test and is usually closely related to the difference between the hypothesized value and the true value of the parameter under study.
• From the relationship between the probability of a Type I and a Type II error (as α (alpha) decreases, β (beta) increases), we can see that as α (alpha) decreases, Power = 1 – β = 1 – beta also decreases.
• There are other mathematical ways to change the power of a hypothesis test, such as changing the population standard deviation; however, these are not quantities that we can usually control so we will not discuss them here.

In practice, we specify a significance level and a desired power to detect a difference which will have practical meaning to us and this determines the sample size required for the experiment or study.

For most grants involving statistical analysis, power calculations must be completed to illustrate that the study will have a reasonable chance to detect an important effect. Otherwise, the money spent on the study could be wasted. The goal is usually to have a power close to 80%.

For example, if there is only a 5% chance to detect an important difference between two treatments in a clinical trial, this would result in a waste of time, effort, and money on the study since, when the alternative hypothesis is true, the chance a treatment effect can be found is very small.

• In order to calculate the power of a hypothesis test, we must specify the “truth.” As we mentioned previously when discussing Type II errors, in practice we can only calculate this probability using a series of “what if” calculations which depend upon the type of problem.

The following activity involves working with an interactive applet to study power more carefully.

Learn by Doing: Power of Hypothesis Tests

The following reading is an excellent discussion about Type I and Type II errors.

(Optional) Outside Reading: A Good Discussion of Power (≈ 2500 words)

We will not be asking you to perform power calculations manually. You may be asked to use online calculators and applets. Most statistical software packages offer some ability to complete power calculations. There are also many online calculators for power and sample size on the internet, for example, Russ Lenth’s power and sample-size page .

Proportions (Introduction & Step 1)

CO-4: Distinguish among different measurement scales, choose the appropriate descriptive and inferential statistical methods based on these distinctions, and interpret the results.

LO 4.33: In a given context, distinguish between situations involving a population proportion and a population mean and specify the correct null and alternative hypothesis for the scenario.

LO 4.34: Carry out a complete hypothesis test for a population proportion by hand.

Video: Proportions (Introduction & Step 1) (7:18)

Now that we understand the process of hypothesis testing and the logic behind it, we are ready to start learning about specific statistical tests (also known as significance tests).

The first test we are going to learn is the test about the population proportion (p).

This test is widely known as the “z-test for the population proportion (p).”

We will understand later where the “z-test” part is coming from.

This will be the only type of problem you will complete entirely “by-hand” in this course. Our goal is to use this example to give you the tools you need to understand how this process works. After working a few problems, you should review the earlier material again. You will likely need to review the terminology and concepts a few times before you fully understand the process.

In reality, you will often be conducting more complex statistical tests and allowing software to provide the p-value. In these settings it will be important to know what test to apply for a given situation and to be able to explain the results in context.

Review: Types of Variables

When we conduct a test about a population proportion, we are working with a categorical variable. Later in the course, after we have learned a variety of hypothesis tests, we will need to be able to identify which test is appropriate for which situation. Identifying the variable as categorical or quantitative is an important component of choosing an appropriate hypothesis test.

Learn by Doing: Review Types of Variables

One Sample Z-Test for a Population Proportion

In this part of our discussion on hypothesis testing, we will go into details that we did not go into before. More specifically, we will use this test to introduce the idea of a test statistic , and details about how p-values are calculated .

Let’s start by introducing the three examples, which will be the leading examples in our discussion. Each example is followed by a figure illustrating the information provided, as well as the question of interest.

A machine is known to produce 20% defective products, and is therefore sent for repair. After the machine is repaired, 400 products produced by the machine are chosen at random and 64 of them are found to be defective. Do the data provide enough evidence that the proportion of defective products produced by the machine (p) has been reduced as a result of the repair?

The following figure displays the information, as well as the question of interest:

The question of interest helps us formulate the null and alternative hypotheses in terms of p, the proportion of defective products produced by the machine following the repair:

• Ho: p = 0.20 (No change; the repair did not help).
• Ha: p < 0.20 (The repair was effective at reducing the proportion of defective parts).

There are rumors that students at a certain liberal arts college are more inclined to use drugs than U.S. college students in general. Suppose that in a simple random sample of 100 students from the college, 19 admitted to marijuana use. Do the data provide enough evidence to conclude that the proportion of marijuana users among the students in the college (p) is higher than the national proportion, which is 0.157? (This number is reported by the Harvard School of Public Health.)

Again, the following figure displays the information as well as the question of interest:

As before, we can formulate the null and alternative hypotheses in terms of p, the proportion of students in the college who use marijuana:

• Ho: p = 0.157 (same as among all college students in the country).
• Ha: p > 0.157 (higher than the national figure).

Polls on certain topics are conducted routinely in order to monitor changes in the public’s opinions over time. One such topic is the death penalty. In 2003 a poll estimated that 64% of U.S. adults support the death penalty for a person convicted of murder. In a more recent poll, 675 out of 1,000 U.S. adults chosen at random were in favor of the death penalty for convicted murderers. Do the results of this poll provide evidence that the proportion of U.S. adults who support the death penalty for convicted murderers (p) changed between 2003 and the later poll?

Here is a figure that displays the information, as well as the question of interest:

Again, we can formulate the null and alternative hypotheses in term of p, the proportion of U.S. adults who support the death penalty for convicted murderers.

• Ho: p = 0.64 (No change from 2003).
• Ha: p ≠ 0.64 (Some change since 2003).

Learn by Doing: Proportions (Overview)

Did I Get This?: Proportions ( Overview )

Recall that there are basically 4 steps in the process of hypothesis testing:

• STEP 1: State the appropriate null and alternative hypotheses, Ho and Ha.
• STEP 2: Obtain a random sample, collect relevant data, and check whether the data meet the conditions under which the test can be used . If the conditions are met, summarize the data using a test statistic.
• STEP 3: Find the p-value of the test.
• STEP 4: Based on the p-value, decide whether or not the results are statistically significant and draw your conclusions in context.
• Note: In practice, we should always consider the practical significance of the results as well as the statistical significance.

We are now going to go through these steps as they apply to the hypothesis testing for the population proportion p. It should be noted that even though the details will be specific to this particular test, some of the ideas that we will add apply to hypothesis testing in general.

Step 1. Stating the Hypotheses

Here again are the three set of hypotheses that are being tested in each of our three examples:

Has the proportion of defective products been reduced as a result of the repair?

Is the proportion of marijuana users in the college higher than the national figure?

Did the proportion of U.S. adults who support the death penalty change between 2003 and a later poll?

The null hypothesis always takes the form:

• Ho: p = some value

and the alternative hypothesis takes one of the following three forms:

• Ha: p < that value (like in example 1) or
• Ha: p > that value (like in example 2) or
• Ha: p ≠ that value (like in example 3).

Note that it was quite clear from the context which form of the alternative hypothesis would be appropriate. The value that is specified in the null hypothesis is called the null value , and is generally denoted by p 0 . We can say, therefore, that in general the null hypothesis about the population proportion (p) would take the form:

• Ho: p = p 0

We write Ho: p = p 0 to say that we are making the hypothesis that the population proportion has the value of p 0 . In other words, p is the unknown population proportion and p 0 is the number we think p might be for the given situation.

The alternative hypothesis takes one of the following three forms (depending on the context):

Ha: p < p 0 (one-sided)

Ha: p > p 0 (one-sided)

Ha: p ≠ p 0 (two-sided)

The first two possible forms of the alternatives (where the = sign in Ho is challenged by < or >) are called one-sided alternatives , and the third form of alternative (where the = sign in Ho is challenged by ≠) is called a two-sided alternative. To understand the intuition behind these names let’s go back to our examples.

Example 3 (death penalty) is a case where we have a two-sided alternative:

In this case, in order to reject Ho and accept Ha we will need to get a sample proportion of death penalty supporters which is very different from 0.64 in either direction, either much larger or much smaller than 0.64.

In example 2 (marijuana use) we have a one-sided alternative:

Here, in order to reject Ho and accept Ha we will need to get a sample proportion of marijuana users which is much higher than 0.157.

Similarly, in example 1 (defective products), where we are testing:

in order to reject Ho and accept Ha, we will need to get a sample proportion of defective products which is much smaller than 0.20.

Learn by Doing: State Hypotheses (Proportions)

Did I Get This?: State Hypotheses (Proportions)

Proportions (Step 2)

Video: Proportions (Step 2) (12:38)

Step 2. Collect Data, Check Conditions, and Summarize Data

After the hypotheses have been stated, the next step is to obtain a sample (on which the inference will be based), collect relevant data , and summarize them.

It is extremely important that our sample is representative of the population about which we want to draw conclusions. This is ensured when the sample is chosen at random. Beyond the practical issue of ensuring representativeness, choosing a random sample has theoretical importance that we will mention later.

In the case of hypothesis testing for the population proportion (p), we will collect data on the relevant categorical variable from the individuals in the sample and start by calculating the sample proportion p-hat (the natural quantity to calculate when the parameter of interest is p).

Let’s go back to our three examples and add this step to our figures.

As we mentioned earlier without going into details, when we summarize the data in hypothesis testing, we go a step beyond calculating the sample statistic and summarize the data with a test statistic . Every test has a test statistic, which to some degree captures the essence of the test. In fact, the p-value, which so far we have looked upon as “the king” (in the sense that everything is determined by it), is actually determined by (or derived from) the test statistic. We will now introduce the test statistic.

The test statistic is a measure of how far the sample proportion p-hat is from the null value p 0 , the value that the null hypothesis claims is the value of p. In other words, since p-hat is what the data estimates p to be, the test statistic can be viewed as a measure of the “distance” between what the data tells us about p and what the null hypothesis claims p to be.

Let’s use our examples to understand this:

The parameter of interest is p, the proportion of defective products following the repair.

The data estimate p to be p-hat = 0.16

The null hypothesis claims that p = 0.20

The data are therefore 0.04 (or 4 percentage points) below the null hypothesis value.

It is hard to evaluate whether this difference of 4% in defective products is enough evidence to say that the repair was effective at reducing the proportion of defective products, but clearly, the larger the difference, the more evidence it is against the null hypothesis. So if, for example, our sample proportion of defective products had been, say, 0.10 instead of 0.16, then I think you would all agree that cutting the proportion of defective products in half (from 20% to 10%) would be extremely strong evidence that the repair was effective at reducing the proportion of defective products.

The parameter of interest is p, the proportion of students in a college who use marijuana.

The data estimate p to be p-hat = 0.19

The null hypothesis claims that p = 0.157

The data are therefore 0.033 (or 3.3. percentage points) above the null hypothesis value.

The parameter of interest is p, the proportion of U.S. adults who support the death penalty for convicted murderers.

The data estimate p to be p-hat = 0.675

The null hypothesis claims that p = 0.64

There is a difference of 0.035 (or 3.5. percentage points) between the data and the null hypothesis value.

The problem with looking only at the difference between the sample proportion, p-hat, and the null value, p 0 is that we have not taken into account the variability of our estimator p-hat which, as we know from our study of sampling distributions, depends on the sample size.

For this reason, the test statistic cannot simply be the difference between p-hat and p 0 , but must be some form of that formula that accounts for the sample size. In other words, we need to somehow standardize the difference so that comparison between different situations will be possible. We are very close to revealing the test statistic, but before we construct it, let’s be reminded of the following two facts from probability:

Fact 1: When we take a random sample of size n from a population with population proportion p, then

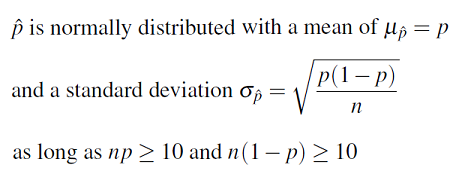
Fact 2: The z-score of any normal value (a value that comes from a normal distribution) is calculated by finding the difference between the value and the mean and then dividing that difference by the standard deviation (of the normal distribution associated with the value). The z-score represents how many standard deviations below or above the mean the value is.

Thus, our test statistic should be a measure of how far the sample proportion p-hat is from the null value p 0 relative to the variation of p-hat (as measured by the standard error of p-hat).

Recall that the standard error is the standard deviation of the sampling distribution for a given statistic. For p-hat, we know the following:

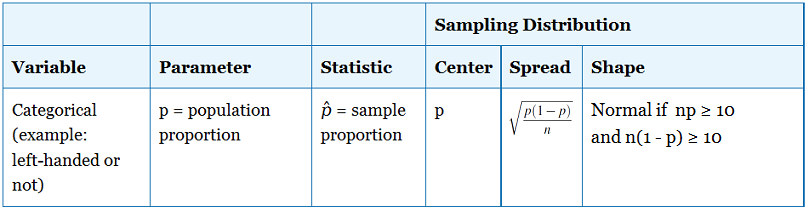
To find the p-value, we will need to determine how surprising our value is assuming the null hypothesis is true. We already have the tools needed for this process from our study of sampling distributions as represented in the table above.

If we assume the null hypothesis is true, we can specify that the center of the distribution of all possible values of p-hat from samples of size 400 would be 0.20 (our null value).

We can calculate the standard error, assuming p = 0.20 as

\(\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}=\sqrt{\dfrac{0.2(1-0.2)}{400}}=0.02\)

The following picture represents the sampling distribution of all possible values of p-hat of samples of size 400, assuming the true proportion p is 0.20 and our other requirements for the sampling distribution to be normal are met (we will review these during the next step).

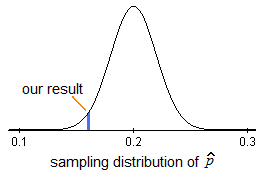
In order to calculate probabilities for the picture above, we would need to find the z-score associated with our result.

This z-score is the test statistic ! In this example, the numerator of our z-score is the difference between p-hat (0.16) and null value (0.20) which we found earlier to be -0.04. The denominator of our z-score is the standard error calculated above (0.02) and thus quickly we find the z-score, our test statistic, to be -2.

The sample proportion based upon this data is 2 standard errors below the null value.

Hopefully you now understand more about the reasons we need probability in statistics!!

Now we will formalize the definition and look at our remaining examples before moving on to the next step, which will be to determine if a normal distribution applies and calculate the p-value.

Test Statistic for Hypothesis Tests for One Proportion is:

\(z=\dfrac{\hat{p}-p_{0}}{\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}}\)

It represents the difference between the sample proportion and the null value, measured in standard deviations (standard error of p-hat).

The picture above is a representation of the sampling distribution of p-hat assuming p = p 0 . In other words, this is a model of how p-hat behaves if we are drawing random samples from a population for which Ho is true.

Notice the center of the sampling distribution is at p 0 , which is the hypothesized proportion given in the null hypothesis (Ho: p = p 0 .) We could also mark the axis in standard error units,

\(\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}\)

For example, if our null hypothesis claims that the proportion of U.S. adults supporting the death penalty is 0.64, then the sampling distribution is drawn as if the null is true. We draw a normal distribution centered at 0.64 (p 0 ) with a standard error dependent on sample size,

\(\sqrt{\dfrac{0.64(1-0.64)}{n}}\).

Important Comment:

• Note that under the assumption that Ho is true (and if the conditions for the sampling distribution to be normal are satisfied) the test statistic follows a N(0,1) (standard normal) distribution. Another way to say the same thing which is quite common is: “The null distribution of the test statistic is N(0,1).”

By “null distribution,” we mean the distribution under the assumption that Ho is true. As we’ll see and stress again later, the null distribution of the test statistic is what the calculation of the p-value is based on.

Let’s go back to our remaining two examples and find the test statistic in each case:

Since the null hypothesis is Ho: p = 0.157, the standardized (z) score of p-hat = 0.19 is

\(z=\dfrac{0.19-0.157}{\sqrt{\dfrac{0.157(1-0.157)}{100}}} \approx 0.91\)

This is the value of the test statistic for this example.

We interpret this to mean that, assuming that Ho is true, the sample proportion p-hat = 0.19 is 0.91 standard errors above the null value (0.157).

Since the null hypothesis is Ho: p = 0.64, the standardized (z) score of p-hat = 0.675 is

\(z=\dfrac{0.675-0.64}{\sqrt{\dfrac{0.64(1-0.64)}{1000}}} \approx 2.31\)

We interpret this to mean that, assuming that Ho is true, the sample proportion p-hat = 0.675 is 2.31 standard errors above the null value (0.64).

Learn by Doing: Proportions (Step 2)

Comments about the Test Statistic:

• We mentioned earlier that to some degree, the test statistic captures the essence of the test. In this case, the test statistic measures the difference between p-hat and p 0 in standard errors. This is exactly what this test is about. Get data, and look at the discrepancy between what the data estimates p to be (represented by p-hat) and what Ho claims about p (represented by p 0 ).
• You can think about this test statistic as a measure of evidence in the data against Ho. The larger the test statistic, the “further the data are from Ho” and therefore the more evidence the data provide against Ho.

Learn by Doing: Proportions (Step 2) Understanding the Test Statistic

Did I Get This?: Proportions (Step 2)

• It should now be clear why this test is commonly known as the z-test for the population proportion . The name comes from the fact that it is based on a test statistic that is a z-score.
• Recall fact 1 that we used for constructing the z-test statistic. Here is part of it again:

When we take a random sample of size n from a population with population proportion p 0 , the possible values of the sample proportion p-hat ( when certain conditions are met ) have approximately a normal distribution with a mean of p 0 … and a standard deviation of

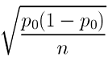
This result provides the theoretical justification for constructing the test statistic the way we did, and therefore the assumptions under which this result holds (in bold, above) are the conditions that our data need to satisfy so that we can use this test. These two conditions are:

i. The sample has to be random.

ii. The conditions under which the sampling distribution of p-hat is normal are met. In other words:

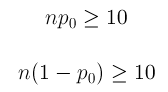
• Here we will pause to say more about condition (i.) above, the need for a random sample. In the Probability Unit we discussed sampling plans based on probability (such as a simple random sample, cluster, or stratified sampling) that produce a non-biased sample, which can be safely used in order to make inferences about a population. We noted in the Probability Unit that, in practice, other (non-random) sampling techniques are sometimes used when random sampling is not feasible. It is important though, when these techniques are used, to be aware of the type of bias that they introduce, and thus the limitations of the conclusions that can be drawn from them. For our purpose here, we will focus on one such practice, the situation in which a sample is not really chosen randomly, but in the context of the categorical variable that is being studied, the sample is regarded as random. For example, say that you are interested in the proportion of students at a certain college who suffer from seasonal allergies. For that purpose, the students in a large engineering class could be considered as a random sample, since there is nothing about being in an engineering class that makes you more or less likely to suffer from seasonal allergies. Technically, the engineering class is a convenience sample, but it is treated as a random sample in the context of this categorical variable. On the other hand, if you are interested in the proportion of students in the college who have math anxiety, then the class of engineering students clearly could not possibly be viewed as a random sample, since engineering students probably have a much lower incidence of math anxiety than the college population overall.

Learn by Doing: Proportions (Step 2) Valid or Invalid Sampling?

Let’s check the conditions in our three examples.

i. The 400 products were chosen at random.

ii. n = 400, p 0 = 0.2 and therefore:

\(n p_{0}=400(0.2)=80 \geq 10\)

\(n\left(1-p_{0}\right)=400(1-0.2)=320 \geq 10\)

i. The 100 students were chosen at random.

ii. n = 100, p 0 = 0.157 and therefore:

\begin{gathered} n p_{0}=100(0.157)=15.7 \geq 10 \\ n\left(1-p_{0}\right)=100(1-0.157)=84.3 \geq 10 \end{gathered}

i. The 1000 adults were chosen at random.

ii. n = 1000, p 0 = 0.64 and therefore:

\begin{gathered} n p_{0}=1000(0.64)=640 \geq 10 \\ n\left(1-p_{0}\right)=1000(1-0.64)=360 \geq 10 \end{gathered}

Learn by Doing: Proportions (Step 2) Verify Conditions

Checking that our data satisfy the conditions under which the test can be reliably used is a very important part of the hypothesis testing process. Be sure to consider this for every hypothesis test you conduct in this course and certainly in practice.

The Four Steps in Hypothesis Testing

With respect to the z-test, the population proportion that we are currently discussing we have:

Step 1: Completed

Step 2: Completed

Step 3: This is what we will work on next.

Proportions (Step 3)

Video: Proportions (Step 3) (14:46)

Calculators and Tables

Step 3. Finding the P-value of the Test

So far we’ve talked about the p-value at the intuitive level: understanding what it is (or what it measures) and how we use it to draw conclusions about the statistical significance of our results. We will now go more deeply into how the p-value is calculated.

It should be mentioned that eventually we will rely on technology to calculate the p-value for us (as well as the test statistic), but in order to make intelligent use of the output, it is important to first understand the details, and only then let the computer do the calculations for us. Again, our goal is to use this simple example to give you the tools you need to understand the process entirely. Let’s start.

Recall that so far we have said that the p-value is the probability of obtaining data like those observed assuming that Ho is true. Like the test statistic, the p-value is, therefore, a measure of the evidence against Ho. In the case of the test statistic, the larger it is in magnitude (positive or negative), the further p-hat is from p 0 , the more evidence we have against Ho. In the case of the p-value , it is the opposite; the smaller it is, the more unlikely it is to get data like those observed when Ho is true, the more evidence it is against Ho . One can actually draw conclusions in hypothesis testing just using the test statistic, and as we’ll see the p-value is, in a sense, just another way of looking at the test statistic. The reason that we actually take the extra step in this course and derive the p-value from the test statistic is that even though in this case (the test about the population proportion) and some other tests, the value of the test statistic has a very clear and intuitive interpretation, there are some tests where its value is not as easy to interpret. On the other hand, the p-value keeps its intuitive appeal across all statistical tests.

How is the p-value calculated?

Intuitively, the p-value is the probability of observing data like those observed assuming that Ho is true. Let’s be a bit more formal:

• Since this is a probability question about the data , it makes sense that the calculation will involve the data summary, the test statistic.
• What do we mean by “like” those observed? By “like” we mean “as extreme or even more extreme.”

Putting it all together, we get that in general:

The p-value is the probability of observing a test statistic as extreme as that observed (or even more extreme) assuming that the null hypothesis is true.

By “extreme” we mean extreme in the direction(s) of the alternative hypothesis.

Specifically , for the z-test for the population proportion:

• If the alternative hypothesis is Ha: p < p 0 (less than) , then “extreme” means small or less than , and the p-value is: The probability of observing a test statistic as small as that observed or smaller if the null hypothesis is true.
• If the alternative hypothesis is Ha: p > p 0 (greater than) , then “extreme” means large or greater than , and the p-value is: The probability of observing a test statistic as large as that observed or larger if the null hypothesis is true.
• If the alternative is Ha: p ≠ p 0 (different from) , then “extreme” means extreme in either direction either small or large (i.e., large in magnitude) or just different from , and the p-value therefore is: The probability of observing a test statistic as large in magnitude as that observed or larger if the null hypothesis is true.(Examples: If z = -2.5: p-value = probability of observing a test statistic as small as -2.5 or smaller or as large as 2.5 or larger. If z = 1.5: p-value = probability of observing a test statistic as large as 1.5 or larger, or as small as -1.5 or smaller.)

OK, hopefully that makes (some) sense. But how do we actually calculate it?

Recall the important comment from our discussion about our test statistic,

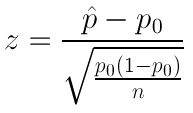
which said that when the null hypothesis is true (i.e., when p = p 0 ), the possible values of our test statistic follow a standard normal (N(0,1), denoted by Z) distribution. Therefore, the p-value calculations (which assume that Ho is true) are simply standard normal distribution calculations for the 3 possible alternative hypotheses.

Alternative Hypothesis is “Less Than”

The probability of observing a test statistic as small as that observed or smaller , assuming that the values of the test statistic follow a standard normal distribution. We will now represent this probability in symbols and also using the normal distribution.

Looking at the shaded region, you can see why this is often referred to as a left-tailed test. We shaded to the left of the test statistic, since less than is to the left.

Alternative Hypothesis is “Greater Than”

The probability of observing a test statistic as large as that observed or larger , assuming that the values of the test statistic follow a standard normal distribution. Again, we will represent this probability in symbols and using the normal distribution

Looking at the shaded region, you can see why this is often referred to as a right-tailed test. We shaded to the right of the test statistic, since greater than is to the right.

Alternative Hypothesis is “Not Equal To”

The probability of observing a test statistic which is as large in magnitude as that observed or larger, assuming that the values of the test statistic follow a standard normal distribution.

This is often referred to as a two-tailed test, since we shaded in both directions.

Next, we will apply this to our three examples. But first, work through the following activities, which should help your understanding.

Learn by Doing: Proportions (Step 3)

Did I Get This?: Proportions (Step 3)

The p-value in this case is:

• The probability of observing a test statistic as small as -2 or smaller, assuming that Ho is true.

OR (recalling what the test statistic actually means in this case),

• The probability of observing a sample proportion that is 2 standard deviations or more below the null value (p 0 = 0.20), assuming that p 0 is the true population proportion.

OR, more specifically,

• The probability of observing a sample proportion of 0.16 or lower in a random sample of size 400, when the true population proportion is p 0 =0.20

In either case, the p-value is found as shown in the following figure:

To find P(Z ≤ -2) we can either use the calculator or table we learned to use in the probability unit for normal random variables. Eventually, after we understand the details, we will use software to run the test for us and the output will give us all the information we need. The p-value that the statistical software provides for this specific example is 0.023. The p-value tells us that it is pretty unlikely (probability of 0.023) to get data like those observed (test statistic of -2 or less) assuming that Ho is true.

• The probability of observing a test statistic as large as 0.91 or larger, assuming that Ho is true.
• The probability of observing a sample proportion that is 0.91 standard deviations or more above the null value (p 0 = 0.157), assuming that p 0 is the true population proportion.
• The probability of observing a sample proportion of 0.19 or higher in a random sample of size 100, when the true population proportion is p 0 =0.157

Again, at this point we can either use the calculator or table to find that the p-value is 0.182, this is P(Z ≥ 0.91).

The p-value tells us that it is not very surprising (probability of 0.182) to get data like those observed (which yield a test statistic of 0.91 or higher) assuming that the null hypothesis is true.

• The probability of observing a test statistic as large as 2.31 (or larger) or as small as -2.31 (or smaller), assuming that Ho is true.
• The probability of observing a sample proportion that is 2.31 standard deviations or more away from the null value (p 0 = 0.64), assuming that p 0 is the true population proportion.
• The probability of observing a sample proportion as different as 0.675 is from 0.64, or even more different (i.e. as high as 0.675 or higher or as low as 0.605 or lower) in a random sample of size 1,000, when the true population proportion is p 0 = 0.64

Again, at this point we can either use the calculator or table to find that the p-value is 0.021, this is P(Z ≤ -2.31) + P(Z ≥ 2.31) = 2*P(Z ≥ |2.31|)

The p-value tells us that it is pretty unlikely (probability of 0.021) to get data like those observed (test statistic as high as 2.31 or higher or as low as -2.31 or lower) assuming that Ho is true.

• We’ve just seen that finding p-values involves probability calculations about the value of the test statistic assuming that Ho is true. In this case, when Ho is true, the values of the test statistic follow a standard normal distribution (i.e., the sampling distribution of the test statistic when the null hypothesis is true is N(0,1)). Therefore, p-values correspond to areas (probabilities) under the standard normal curve.

Similarly, in any test , p-values are found using the sampling distribution of the test statistic when the null hypothesis is true (also known as the “null distribution” of the test statistic). In this case, it was relatively easy to argue that the null distribution of our test statistic is N(0,1). As we’ll see, in other tests, other distributions come up (like the t-distribution and the F-distribution), which we will just mention briefly, and rely heavily on the output of our statistical package for obtaining the p-values.

We’ve just completed our discussion about the p-value, and how it is calculated both in general and more specifically for the z-test for the population proportion. Let’s go back to the four-step process of hypothesis testing and see what we’ve covered and what still needs to be discussed.

With respect to the z-test the population proportion:

Step 3: Completed

Step 4. This is what we will work on next.

Learn by Doing: Proportions (Step 3) Understanding P-values

Proportions (Step 4 & Summary)

Video: Proportions (Step 4 & Summary) (4:30)

Step 4. Drawing Conclusions Based on the P-Value

This last part of the four-step process of hypothesis testing is the same across all statistical tests, and actually, we’ve already said basically everything there is to say about it, but it can’t hurt to say it again.

The p-value is a measure of how much evidence the data present against Ho. The smaller the p-value, the more evidence the data present against Ho.

We already mentioned that what determines what constitutes enough evidence against Ho is the significance level (α, alpha), a cutoff point below which the p-value is considered small enough to reject Ho in favor of Ha. The most commonly used significance level is 0.05.

• Conclusion: There IS enough evidence that Ha is True
• Conclusion: There IS NOT enough evidence that Ha is True

Where instead of Ha is True , we write what this means in the words of the problem, in other words, in the context of the current scenario.

It is important to mention again that this step has essentially two sub-steps:

(i) Based on the p-value, determine whether or not the results are statistically significant (i.e., the data present enough evidence to reject Ho).

(ii) State your conclusions in the context of the problem.

Note: We always still must consider whether the results have any practical significance, particularly if they are statistically significant as a statistically significant result which has not practical use is essentially meaningless!

Let’s go back to our three examples and draw conclusions.

We found that the p-value for this test was 0.023.

Since 0.023 is small (in particular, 0.023 < 0.05), the data provide enough evidence to reject Ho.

Conclusion:

• There IS enough evidence that the proportion of defective products is less than 20% after the repair .

The following figure is the complete story of this example, and includes all the steps we went through, starting from stating the hypotheses and ending with our conclusions:

We found that the p-value for this test was 0.182.

Since .182 is not small (in particular, 0.182 > 0.05), the data do not provide enough evidence to reject Ho.

• There IS NOT enough evidence that the proportion of students at the college who use marijuana is higher than the national figure.

Here is the complete story of this example:

Learn by Doing: Learn by Doing – Proportions (Step 4)

We found that the p-value for this test was 0.021.

Since 0.021 is small (in particular, 0.021 < 0.05), the data provide enough evidence to reject Ho

• There IS enough evidence that the proportion of adults who support the death penalty for convicted murderers has changed since 2003.

Did I Get This?: Proportions (Step 4)

Many Students Wonder: Hypothesis Testing for the Population Proportion

Many students wonder why 5% is often selected as the significance level in hypothesis testing, and why 1% is the next most typical level. This is largely due to just convenience and tradition.

When Ronald Fisher (one of the founders of modern statistics) published one of his tables, he used a mathematically convenient scale that included 5% and 1%. Later, these same 5% and 1% levels were used by other people, in part just because Fisher was so highly esteemed. But mostly these are arbitrary levels.

The idea of selecting some sort of relatively small cutoff was historically important in the development of statistics; but it’s important to remember that there is really a continuous range of increasing confidence towards the alternative hypothesis, not a single all-or-nothing value. There isn’t much meaningful difference, for instance, between a p-value of .049 or .051, and it would be foolish to declare one case definitely a “real” effect and to declare the other case definitely a “random” effect. In either case, the study results were roughly 5% likely by chance if there’s no actual effect.

Whether such a p-value is sufficient for us to reject a particular null hypothesis ultimately depends on the risk of making the wrong decision, and the extent to which the hypothesized effect might contradict our prior experience or previous studies.

Let’s Summarize!!

We have now completed going through the four steps of hypothesis testing, and in particular we learned how they are applied to the z-test for the population proportion. Here is a brief summary:

Step 1: State the hypotheses

State the null hypothesis:

State the alternative hypothesis:

where the choice of the appropriate alternative (out of the three) is usually quite clear from the context of the problem. If you feel it is not clear, it is most likely a two-sided problem. Students are usually good at recognizing the “more than” and “less than” terminology but differences can sometimes be more difficult to spot, sometimes this is because you have preconceived ideas of how you think it should be! Use only the information given in the problem.

Step 2: Obtain data, check conditions, and summarize data

Obtain data from a sample and:

(i) Check whether the data satisfy the conditions which allow you to use this test.

random sample (or at least a sample that can be considered random in context)

the conditions under which the sampling distribution of p-hat is normal are met

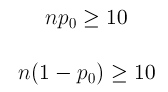
(ii) Calculate the sample proportion p-hat, and summarize the data using the test statistic:

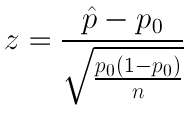
( Recall: This standardized test statistic represents how many standard deviations above or below p 0 our sample proportion p-hat is.)

Step 3: Find the p-value of the test by using the test statistic as follows

IMPORTANT FACT: In all future tests, we will rely on software to obtain the p-value.

When the alternative hypothesis is “less than” the probability of observing a test statistic as small as that observed or smaller , assuming that the values of the test statistic follow a standard normal distribution. We will now represent this probability in symbols and also using the normal distribution.

When the alternative hypothesis is “greater than” the probability of observing a test statistic as large as that observed or larger , assuming that the values of the test statistic follow a standard normal distribution. Again, we will represent this probability in symbols and using the normal distribution

When the alternative hypothesis is “not equal to” the probability of observing a test statistic which is as large in magnitude as that observed or larger, assuming that the values of the test statistic follow a standard normal distribution.

Step 4: Conclusion

Reach a conclusion first regarding the statistical significance of the results, and then determine what it means in the context of the problem.

If p-value ≤ 0.05 then WE REJECT Ho Conclusion: There IS enough evidence that Ha is True

If p-value > 0.05 then WE FAIL TO REJECT Ho Conclusion: There IS NOT enough evidence that Ha is True

Recall that: If the p-value is small (in particular, smaller than the significance level, which is usually 0.05), the results are statistically significant (in the sense that there is a statistically significant difference between what was observed in the sample and what was claimed in Ho), and so we reject Ho.

If the p-value is not small, we do not have enough statistical evidence to reject Ho, and so we continue to believe that Ho may be true. ( Remember: In hypothesis testing we never “accept” Ho ).

Finally, in practice, we should always consider the practical significance of the results as well as the statistical significance.

Learn by Doing: Z-Test for a Population Proportion

What’s next?

Before we move on to the next test, we are going to use the z-test for proportions to bring up and illustrate a few more very important issues regarding hypothesis testing. This might also be a good time to review the concepts of Type I error, Type II error, and Power before continuing on.

More about Hypothesis Testing

CO-1: Describe the roles biostatistics serves in the discipline of public health.

LO 1.11: Recognize the distinction between statistical significance and practical significance.

LO 6.30: Use a confidence interval to determine the correct conclusion to the associated two-sided hypothesis test.

Video: More about Hypothesis Testing (18:25)

The issues regarding hypothesis testing that we will discuss are:

• The effect of sample size on hypothesis testing.
• Statistical significance vs. practical importance.
• Hypothesis testing and confidence intervals—how are they related?

Let’s begin.

1. The Effect of Sample Size on Hypothesis Testing

We have already seen the effect that the sample size has on inference, when we discussed point and interval estimation for the population mean (μ, mu) and population proportion (p). Intuitively …

Larger sample sizes give us more information to pin down the true nature of the population. We can therefore expect the sample mean and sample proportion obtained from a larger sample to be closer to the population mean and proportion, respectively. As a result, for the same level of confidence, we can report a smaller margin of error, and get a narrower confidence interval. What we’ve seen, then, is that larger sample size gives a boost to how much we trust our sample results.

In hypothesis testing, larger sample sizes have a similar effect. We have also discussed that the power of our test increases when the sample size increases, all else remaining the same. This means, we have a better chance to detect the difference between the true value and the null value for larger samples.

The following two examples will illustrate that a larger sample size provides more convincing evidence (the test has greater power), and how the evidence manifests itself in hypothesis testing. Let’s go back to our example 2 (marijuana use at a certain liberal arts college).

We do not have enough evidence to conclude that the proportion of students at the college who use marijuana is higher than the national figure.

Now, let’s increase the sample size.

There are rumors that students in a certain liberal arts college are more inclined to use drugs than U.S. college students in general. Suppose that in a simple random sample of 400 students from the college, 76 admitted to marijuana use . Do the data provide enough evidence to conclude that the proportion of marijuana users among the students in the college (p) is higher than the national proportion, which is 0.157? (Reported by the Harvard School of Public Health).

Our results here are statistically significant . In other words, in example 2* the data provide enough evidence to reject Ho.

• Conclusion: There is enough evidence that the proportion of marijuana users at the college is higher than among all U.S. students.

What do we learn from this?

We see that sample results that are based on a larger sample carry more weight (have greater power).

In example 2, we saw that a sample proportion of 0.19 based on a sample of size of 100 was not enough evidence that the proportion of marijuana users in the college is higher than 0.157. Recall, from our general overview of hypothesis testing, that this conclusion (not having enough evidence to reject the null hypothesis) doesn’t mean the null hypothesis is necessarily true (so, we never “accept” the null); it only means that the particular study didn’t yield sufficient evidence to reject the null. It might be that the sample size was simply too small to detect a statistically significant difference.

However, in example 2*, we saw that when the sample proportion of 0.19 is obtained from a sample of size 400, it carries much more weight, and in particular, provides enough evidence that the proportion of marijuana users in the college is higher than 0.157 (the national figure). In this case, the sample size of 400 was large enough to detect a statistically significant difference.

The following activity will allow you to practice the ideas and terminology used in hypothesis testing when a result is not statistically significant.

Learn by Doing: Interpreting Non-significant Results

2. Statistical significance vs. practical importance.

Now, we will address the issue of statistical significance versus practical importance (which also involves issues of sample size).

The following activity will let you explore the effect of the sample size on the statistical significance of the results yourself, and more importantly will discuss issue 2: Statistical significance vs. practical importance.

Important Fact: In general, with a sufficiently large sample size you can make any result that has very little practical importance statistically significant! A large sample size alone does NOT make a “good” study!!

This suggests that when interpreting the results of a test, you should always think not only about the statistical significance of the results but also about their practical importance.

Learn by Doing: Statistical vs. Practical Significance

3. Hypothesis Testing and Confidence Intervals

The last topic we want to discuss is the relationship between hypothesis testing and confidence intervals. Even though the flavor of these two forms of inference is different (confidence intervals estimate a parameter, and hypothesis testing assesses the evidence in the data against one claim and in favor of another), there is a strong link between them.

We will explain this link (using the z-test and confidence interval for the population proportion), and then explain how confidence intervals can be used after a test has been carried out.

Recall that a confidence interval gives us a set of plausible values for the unknown population parameter. We may therefore examine a confidence interval to informally decide if a proposed value of population proportion seems plausible.

For example, if a 95% confidence interval for p, the proportion of all U.S. adults already familiar with Viagra in May 1998, was (0.61, 0.67), then it seems clear that we should be able to reject a claim that only 50% of all U.S. adults were familiar with the drug, since based on the confidence interval, 0.50 is not one of the plausible values for p.

In fact, the information provided by a confidence interval can be formally related to the information provided by a hypothesis test. ( Comment: The relationship is more straightforward for two-sided alternatives, and so we will not present results for the one-sided cases.)

Suppose we want to carry out the two-sided test:

• Ha: p ≠ p 0

using a significance level of 0.05.

An alternative way to perform this test is to find a 95% confidence interval for p and check:

• If p 0 falls outside the confidence interval, reject Ho.
• If p 0 falls inside the confidence interval, do not reject Ho.

In other words,

• If p 0 is not one of the plausible values for p, we reject Ho.
• If p 0 is a plausible value for p, we cannot reject Ho.

( Comment: Similarly, the results of a test using a significance level of 0.01 can be related to the 99% confidence interval.)

Let’s look at an example:

Recall example 3, where we wanted to know whether the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, when it was 0.64.

We are testing:

and as the figure reminds us, we took a sample of 1,000 U.S. adults, and the data told us that 675 supported the death penalty for convicted murderers (p-hat = 0.675).

A 95% confidence interval for p, the proportion of all U.S. adults who support the death penalty, is:

\(0.675 \pm 1.96 \sqrt{\dfrac{0.675(1-0.675)}{1000}} \approx 0.675 \pm 0.029=(0.646,0.704)\)

Since the 95% confidence interval for p does not include 0.64 as a plausible value for p, we can reject Ho and conclude (as we did before) that there is enough evidence that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003.

You and your roommate are arguing about whose turn it is to clean the apartment. Your roommate suggests that you settle this by tossing a coin and takes one out of a locked box he has on the shelf. Suspecting that the coin might not be fair, you decide to test it first. You toss the coin 80 times, thinking to yourself that if, indeed, the coin is fair, you should get around 40 heads. Instead you get 48 heads. You are puzzled. You are not sure whether getting 48 heads out of 80 is enough evidence to conclude that the coin is unbalanced, or whether this a result that could have happened just by chance when the coin is fair.

Statistics can help you answer this question.

Let p be the true proportion (probability) of heads. We want to test whether the coin is fair or not.

• Ho: p = 0.5 (the coin is fair).
• Ha: p ≠ 0.5 (the coin is not fair).

The data we have are that out of n = 80 tosses, we got 48 heads, or that the sample proportion of heads is p-hat = 48/80 = 0.6.

A 95% confidence interval for p, the true proportion of heads for this coin, is:

\(0.6 \pm 1.96 \sqrt{\dfrac{0.6(1-0.6)}{80}} \approx 0.6 \pm 0.11=(0.49,0.71)\)

Since in this case 0.5 is one of the plausible values for p, we cannot reject Ho. In other words, the data do not provide enough evidence to conclude that the coin is not fair.

The context of the last example is a good opportunity to bring up an important point that was discussed earlier.

Even though we use 0.05 as a cutoff to guide our decision about whether the results are statistically significant, we should not treat it as inviolable and we should always add our own judgment. Let’s look at the last example again.

It turns out that the p-value of this test is 0.0734. In other words, it is maybe not extremely unlikely, but it is quite unlikely (probability of 0.0734) that when you toss a fair coin 80 times you’ll get a sample proportion of heads of 48/80 = 0.6 (or even more extreme). It is true that using the 0.05 significance level (cutoff), 0.0734 is not considered small enough to conclude that the coin is not fair. However, if you really don’t want to clean the apartment, the p-value might be small enough for you to ask your roommate to use a different coin, or to provide one yourself!

Did I Get This?: Connection between Confidence Intervals and Hypothesis Tests

Did I Get This?: Hypothesis Tests for Proportions (Extra Practice)

Here is our final point on this subject:

When the data provide enough evidence to reject Ho, we can conclude (depending on the alternative hypothesis) that the population proportion is either less than, greater than, or not equal to the null value p 0 . However, we do not get a more informative statement about its actual value. It might be of interest, then, to follow the test with a 95% confidence interval that will give us more insight into the actual value of p.

In our example 3,

we concluded that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, when it was 0.64. It is probably of interest not only to know that the proportion has changed, but also to estimate what it has changed to. We’ve calculated the 95% confidence interval for p on the previous page and found that it is (0.646, 0.704).

We can combine our conclusions from the test and the confidence interval and say:

Data provide evidence that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, and we are 95% confident that it is now between 0.646 and 0.704. (i.e. between 64.6% and 70.4%).

Let’s look at our example 1 to see how a confidence interval following a test might be insightful in a different way.

Here is a summary of example 1:

We conclude that as a result of the repair, the proportion of defective products has been reduced to below 0.20 (which was the proportion prior to the repair). It is probably of great interest to the company not only to know that the proportion of defective has been reduced, but also estimate what it has been reduced to, to get a better sense of how effective the repair was. A 95% confidence interval for p in this case is:

\(0.16 \pm 1.96 \sqrt{\dfrac{0.16(1-0.16)}{400}} \approx 0.16 \pm 0.036=(0.124,0.196)\)

We can therefore say that the data provide evidence that the proportion of defective products has been reduced, and we are 95% confident that it has been reduced to somewhere between 12.4% and 19.6%. This is very useful information, since it tells us that even though the results were significant (i.e., the repair reduced the number of defective products), the repair might not have been effective enough, if it managed to reduce the number of defective products only to the range provided by the confidence interval. This, of course, ties back in to the idea of statistical significance vs. practical importance that we discussed earlier. Even though the results are statistically significant (Ho was rejected), practically speaking, the repair might still be considered ineffective.

Learn by Doing: Hypothesis Tests and Confidence Intervals

Even though this portion of the current section is about the z-test for population proportion, it is loaded with very important ideas that apply to hypothesis testing in general. We’ve already summarized the details that are specific to the z-test for proportions, so the purpose of this summary is to highlight the general ideas.

The process of hypothesis testing has four steps :

I. Stating the null and alternative hypotheses (Ho and Ha).

II. Obtaining a random sample (or at least one that can be considered random) and collecting data. Using the data:

Check that the conditions under which the test can be reliably used are met.

Summarize the data using a test statistic.

• The test statistic is a measure of the evidence in the data against Ho. The larger the test statistic is in magnitude, the more evidence the data present against Ho.

III. Finding the p-value of the test. The p-value is the probability of getting data like those observed (or even more extreme) assuming that the null hypothesis is true, and is calculated using the null distribution of the test statistic. The p-value is a measure of the evidence against Ho. The smaller the p-value, the more evidence the data present against Ho.

IV. Making conclusions.

Conclusions about the statistical significance of the results:

If the p-value is small, the data present enough evidence to reject Ho (and accept Ha).

If the p-value is not small, the data do not provide enough evidence to reject Ho.

To help guide our decision, we use the significance level as a cutoff for what is considered a small p-value. The significance cutoff is usually set at 0.05.

Conclusions should then be provided in the context of the problem.

Additional Important Ideas about Hypothesis Testing

• Results that are based on a larger sample carry more weight, and therefore as the sample size increases, results become more statistically significant.
• Even a very small and practically unimportant effect becomes statistically significant with a large enough sample size. The distinction between statistical significance and practical importance should therefore always be considered.
• Confidence intervals can be used in order to carry out two-sided tests (95% confidence for the 0.05 significance level). If the null value is not included in the confidence interval (i.e., is not one of the plausible values for the parameter), we have enough evidence to reject Ho. Otherwise, we cannot reject Ho.
• If the results are statistically significant, it might be of interest to follow up the tests with a confidence interval in order to get insight into the actual value of the parameter of interest.
• It is important to be aware that there are two types of errors in hypothesis testing ( Type I and Type II ) and that the power of a statistical test is an important measure of how likely we are to be able to detect a difference of interest to us in a particular problem.

Means (All Steps)

NOTE: Beginning on this page, the Learn By Doing and Did I Get This activities are presented as interactive PDF files. The interactivity may not work on mobile devices or with certain PDF viewers. Use an official ADOBE product such as ADOBE READER .

If you have any issues with the Learn By Doing or Did I Get This interactive PDF files, you can view all of the questions and answers presented on this page in this document:

• QUESTION/Answer (SPOILER ALERT!)

Tests About μ (mu) When σ (sigma) is Unknown – The t-test for a Population Mean

The t-distribution.

Video: Means (All Steps) (13:11)

So far we have talked about the logic behind hypothesis testing and then illustrated how this process proceeds in practice, using the z-test for the population proportion (p).

We are now moving on to discuss testing for the population mean (μ, mu), which is the parameter of interest when the variable of interest is quantitative.

A few comments about the structure of this section:

• The basic groundwork for carrying out hypothesis tests has already been laid in our general discussion and in our presentation of tests about proportions.

Therefore we can easily modify the four steps to carry out tests about means instead, without going into all of the details again.

We will use this approach for all future tests so be sure to go back to the discussion in general and for proportions to review the concepts in more detail.

• In our discussion about confidence intervals for the population mean, we made the distinction between whether the population standard deviation, σ (sigma) was known or if we needed to estimate this value using the sample standard deviation, s .

In this section, we will only discuss the second case as in most realistic settings we do not know the population standard deviation .

In this case we need to use the t- distribution instead of the standard normal distribution for the probability aspects of confidence intervals (choosing table values) and hypothesis tests (finding p-values).

• Although we will discuss some theoretical or conceptual details for some of the analyses we will learn, from this point on we will rely on software to conduct tests and calculate confidence intervals for us , while we focus on understanding which methods are used for which situations and what the results say in context.

If you are interested in more information about the z-test, where we assume the population standard deviation σ (sigma) is known, you can review the Carnegie Mellon Open Learning Statistics Course (you will need to click “ENTER COURSE”).

Like any other tests, the t- test for the population mean follows the four-step process:

• STEP 1: Stating the hypotheses H o and H a .
• STEP 2: Collecting relevant data, checking that the data satisfy the conditions which allow us to use this test, and summarizing the data using a test statistic.
• STEP 3: Finding the p-value of the test, the probability of obtaining data as extreme as those collected (or even more extreme, in the direction of the alternative hypothesis), assuming that the null hypothesis is true. In other words, how likely is it that the only reason for getting data like those observed is sampling variability (and not because H o is not true)?
• STEP 4: Drawing conclusions, assessing the statistical significance of the results based on the p-value, and stating our conclusions in context. (Do we or don’t we have evidence to reject H o and accept H a ?)
• Note: In practice, we should also always consider the practical significance of the results as well as the statistical significance.

We will now go through the four steps specifically for the t- test for the population mean and apply them to our two examples.

Only in a few cases is it reasonable to assume that the population standard deviation, σ (sigma), is known and so we will not cover hypothesis tests in this case. We discussed both cases for confidence intervals so that we could still calculate some confidence intervals by hand.

For this and all future tests we will rely on software to obtain our summary statistics, test statistics, and p-values for us.

The case where σ (sigma) is unknown is much more common in practice. What can we use to replace σ (sigma)? If you don’t know the population standard deviation, the best you can do is find the sample standard deviation, s, and use it instead of σ (sigma). (Note that this is exactly what we did when we discussed confidence intervals).

Is that it? Can we just use s instead of σ (sigma), and the rest is the same as the previous case? Unfortunately, it’s not that simple, but not very complicated either.

Here, when we use the sample standard deviation, s, as our estimate of σ (sigma) we can no longer use a normal distribution to find the cutoff for confidence intervals or the p-values for hypothesis tests.

Instead we must use the t- distribution (with n-1 degrees of freedom) to obtain the p-value for this test.

We discussed this issue for confidence intervals. We will talk more about the t- distribution after we discuss the details of this test for those who are interested in learning more.

It isn’t really necessary for us to understand this distribution but it is important that we use the correct distributions in practice via our software.

We will wait until UNIT 4B to look at how to accomplish this test in the software. For now focus on understanding the process and drawing the correct conclusions from the p-values given.

Now let’s go through the four steps in conducting the t- test for the population mean.

The null and alternative hypotheses for the t- test for the population mean (μ, mu) have exactly the same structure as the hypotheses for z-test for the population proportion (p):

The null hypothesis has the form:

• Ho: μ = μ 0 (mu = mu_zero)

(where μ 0 (mu_zero) is often called the null value)

• Ha: μ < μ 0 (mu < mu_zero) (one-sided)
• Ha: μ > μ 0 (mu > mu_zero) (one-sided)
• Ha: μ ≠ μ 0 (mu ≠ mu_zero) (two-sided)

where the choice of the appropriate alternative (out of the three) is usually quite clear from the context of the problem.

If you feel it is not clear, it is most likely a two-sided problem. Students are usually good at recognizing the “more than” and “less than” terminology but differences can sometimes be more difficult to spot, sometimes this is because you have preconceived ideas of how you think it should be! You also cannot use the information from the sample to help you determine the hypothesis. We would not know our data when we originally asked the question.

Now try it yourself. Here are a few exercises on stating the hypotheses for tests for a population mean.

Learn by Doing: State the Hypotheses for a test for a population mean

Here are a few more activities for practice.

Did I Get This?: State the Hypotheses for a test for a population mean

When setting up hypotheses, be sure to use only the information in the research question. We cannot use our sample data to help us set up our hypotheses.

For this test, it is still important to correctly choose the alternative hypothesis as “less than”, “greater than”, or “different” although generally in practice two-sample tests are used.

Obtain data from a sample:

• In this step we would obtain data from a sample. This is not something we do much of in courses but it is done very often in practice!

Check the conditions:

• Then we check the conditions under which this test (the t- test for one population mean) can be safely carried out – which are:
• The sample is random (or at least can be considered random in context).
• We are in one of the three situations marked with a green check mark in the following table (which ensure that x-bar is at least approximately normal and the test statistic using the sample standard deviation, s, is therefore a t- distribution with n-1 degrees of freedom – proving this is beyond the scope of this course):
• For large samples, we don’t need to check for normality in the population . We can rely on the sample size as the basis for the validity of using this test.
• For small samples , we need to have data from a normal population in order for the p-values and confidence intervals to be valid.

In practice, for small samples, it can be very difficult to determine if the population is normal. Here is a simulation to give you a better understanding of the difficulties.

Video: Simulations – Are Samples from a Normal Population? (4:58)

Now try it yourself with a few activities.

Learn by Doing: Checking Conditions for Hypothesis Testing for the Population Mean

• It is always a good idea to look at the data and get a sense of their pattern regardless of whether you actually need to do it in order to assess whether the conditions are met.
• This idea of looking at the data is relevant to all tests in general. In the next module—inference for relationships—conducting exploratory data analysis before inference will be an integral part of the process.

Here are a few more problems for extra practice.

Did I Get This?: Checking Conditions for Hypothesis Testing for the Population Mean

When setting up hypotheses, be sure to use only the information in the res

Calculate Test Statistic

Assuming that the conditions are met, we calculate the sample mean x-bar and the sample standard deviation, s (which estimates σ (sigma)), and summarize the data with a test statistic.

The test statistic for the t -test for the population mean is:

\(t=\dfrac{\bar{x} - \mu_0}{s/ \sqrt{n}}\)

Recall that such a standardized test statistic represents how many standard deviations above or below μ 0 (mu_zero) our sample mean x-bar is.

Therefore our test statistic is a measure of how different our data are from what is claimed in the null hypothesis. This is an idea that we mentioned in the previous test as well.

Again we will rely on the p-value to determine how unusual our data would be if the null hypothesis is true.

As we mentioned, the test statistic in the t -test for a population mean does not follow a standard normal distribution. Rather, it follows another bell-shaped distribution called the t- distribution.

We will present the details of this distribution at the end for those interested but for now we will work on the process of the test.

Here are a few important facts.

• In statistical language we say that the null distribution of our test statistic is the t- distribution with (n-1) degrees of freedom. In other words, when Ho is true (i.e., when μ = μ 0 (mu = mu_zero)), our test statistic has a t- distribution with (n-1) d.f., and this is the distribution under which we find p-values.
• For a large sample size (n), the null distribution of the test statistic is approximately Z, so whether we use t (n – 1) or Z to calculate the p-values does not make a big difference. However, software will use the t -distribution regardless of the sample size and so will we.

Although we will not calculate p-values by hand for this test, we can still easily calculate the test statistic.

Try it yourself:

Learn by Doing: Calculate the Test Statistic for a Test for a Population Mean

From this point in this course and certainly in practice we will allow the software to calculate our test statistics and we will use the p-values provided to draw our conclusions.

We will use software to obtain the p-value for this (and all future) tests but here are the images illustrating how the p-value is calculated in each of the three cases corresponding to the three choices for our alternative hypothesis.

Note that due to the symmetry of the t distribution, for a given value of the test statistic t, the p-value for the two-sided test is twice as large as the p-value of either of the one-sided tests. The same thing happens when p-values are calculated under the t distribution as when they are calculated under the Z distribution.

We will show some examples of p-values obtained from software in our examples. For now let’s continue our summary of the steps.

As usual, based on the p-value (and some significance level of choice) we assess the statistical significance of results, and draw our conclusions in context.

To review what we have said before:

If p-value ≤ 0.05 then WE REJECT Ho

If p-value > 0.05 then WE FAIL TO REJECT Ho

This step has essentially two sub-steps:

We are now ready to look at two examples.

A certain prescription medicine is supposed to contain an average of 250 parts per million (ppm) of a certain chemical. If the concentration is higher than this, the drug may cause harmful side effects; if it is lower, the drug may be ineffective.

The manufacturer runs a check to see if the mean concentration in a large shipment conforms to the target level of 250 ppm or not.

A simple random sample of 100 portions is tested, and the sample mean concentration is found to be 247 ppm with a sample standard deviation of 12 ppm.

Here is a figure that represents this example:

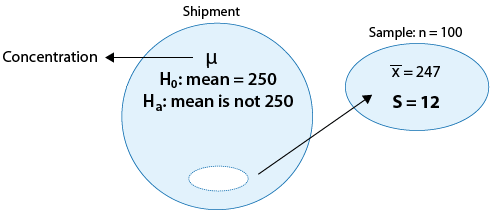
1. The hypotheses being tested are:

• Ha: μ ≠ μ 0 (mu ≠ mu_zero)
• Where μ = population mean part per million of the chemical in the entire shipment

2. The conditions that allow us to use the t-test are met since:

• The sample is random
• The sample size is large enough for the Central Limit Theorem to apply and ensure the normality of x-bar. We do not need normality of the population in order to be able to conduct this test for the population mean. We are in the 2 nd column in the table below.
• The test statistic is:

\(t=\dfrac{\bar{x}-\mu_{0}}{s / \sqrt{n}}=\dfrac{247-250}{12 / \sqrt{100}}=-2.5\)

• The data (represented by the sample mean) are 2.5 standard errors below the null value.

3. Finding the p-value.

• To find the p-value we use statistical software, and we calculate a p-value of 0.014.

4. Conclusions:

• The p-value is small (.014) indicating that at the 5% significance level, the results are significant.
• We reject the null hypothesis.
• There is enough evidence to conclude that the mean concentration in entire shipment is not the required 250 ppm.
• It is difficult to comment on the practical significance of this result without more understanding of the practical considerations of this problem.

Here is a summary:

• The 95% confidence interval for μ (mu) can be used here in the same way as for proportions to conduct the two-sided test (checking whether the null value falls inside or outside the confidence interval) or following a t- test where Ho was rejected to get insight into the value of μ (mu).
• We find the 95% confidence interval to be (244.619, 249.381) . Since 250 is not in the interval we know we would reject our null hypothesis that μ (mu) = 250. The confidence interval gives additional information. By accounting for estimation error, it estimates that the population mean is likely to be between 244.62 and 249.38. This is lower than the target concentration and that information might help determine the seriousness and appropriate course of action in this situation.

In most situations in practice we use TWO-SIDED HYPOTHESIS TESTS, followed by confidence intervals to gain more insight.

For completeness in covering one sample t-tests for a population mean, we still cover all three possible alternative hypotheses here HOWEVER, this will be the last test for which we will do so.

A research study measured the pulse rates of 57 college men and found a mean pulse rate of 70 beats per minute with a standard deviation of 9.85 beats per minute.

Researchers want to know if the mean pulse rate for all college men is different from the current standard of 72 beats per minute.

• The hypotheses being tested are:
• Ho: μ = 72
• Ha: μ ≠ 72
• Where μ = population mean heart rate among college men
• The conditions that allow us to use the t- test are met since:
• The sample is random.
• The sample size is large (n = 57) so we do not need normality of the population in order to be able to conduct this test for the population mean. We are in the 2 nd column in the table below.

\(t=\dfrac{\bar{x}-\mu}{s / \sqrt{n}}=\dfrac{70-72}{9.85 / \sqrt{57}}=-1.53\)

• The data (represented by the sample mean) are 1.53 estimated standard errors below the null value.
• Recall that in general the p-value is calculated under the null distribution of the test statistic, which, in the t- test case, is t (n-1). In our case, in which n = 57, the p-value is calculated under the t (56) distribution. Using statistical software, we find that the p-value is 0.132 .
• Here is how we calculated the p-value. http://homepage.stat.uiowa.edu/~mbognar/applets/t.html .

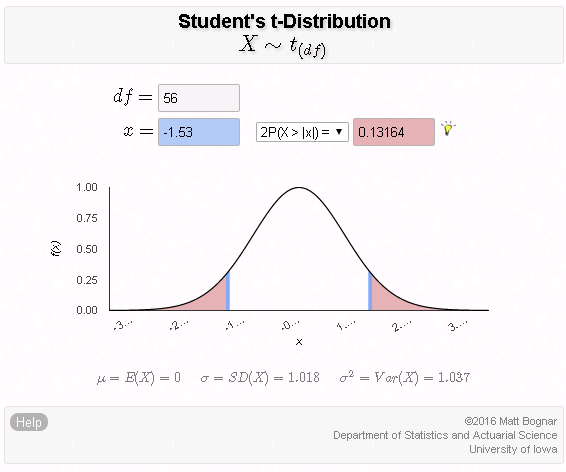
4. Making conclusions.

• The p-value (0.132) is not small, indicating that the results are not significant.
• We fail to reject the null hypothesis.
• There is not enough evidence to conclude that the mean pulse rate for all college men is different from the current standard of 72 beats per minute.
• The results from this sample do not appear to have any practical significance either with a mean pulse rate of 70, this is very similar to the hypothesized value, relative to the variation expected in pulse rates.

Now try a few yourself.

Learn by Doing: Hypothesis Testing for the Population Mean

From this point in this course and certainly in practice we will allow the software to calculate our test statistic and p-value and we will use the p-values provided to draw our conclusions.

That concludes our discussion of hypothesis tests in Unit 4A.

In the next unit we will continue to use both confidence intervals and hypothesis test to investigate the relationship between two variables in the cases we covered in Unit 1 on exploratory data analysis – we will look at Case CQ, Case CC, and Case QQ.

Before moving on, we will discuss the details about the t- distribution as a general object.

We have seen that variables can be visually modeled by many different sorts of shapes, and we call these shapes distributions. Several distributions arise so frequently that they have been given special names, and they have been studied mathematically.

So far in the course, the only one we’ve named, for continuous quantitative variables, is the normal distribution, but there are others. One of them is called the t- distribution.

The t- distribution is another bell-shaped (unimodal and symmetric) distribution, like the normal distribution; and the center of the t- distribution is standardized at zero, like the center of the standard normal distribution.

Like all distributions that are used as probability models, the normal and the t- distribution are both scaled, so the total area under each of them is 1.

So how is the t-distribution fundamentally different from the normal distribution?

• The spread .

The following picture illustrates the fundamental difference between the normal distribution and the t-distribution:

Here we have an image which illustrates the fundamental difference between the normal distribution and the t- distribution:

You can see in the picture that the t- distribution has slightly less area near the expected central value than the normal distribution does, and you can see that the t distribution has correspondingly more area in the “tails” than the normal distribution does. (It’s often said that the t- distribution has “fatter tails” or “heavier tails” than the normal distribution.)

This reflects the fact that the t- distribution has a larger spread than the normal distribution. The same total area of 1 is spread out over a slightly wider range on the t- distribution, making it a bit lower near the center compared to the normal distribution, and giving the t- distribution slightly more probability in the ‘tails’ compared to the normal distribution.

Therefore, the t- distribution ends up being the appropriate model in certain cases where there is more variability than would be predicted by the normal distribution. One of these cases is stock values, which have more variability (or “volatility,” to use the economic term) than would be predicted by the normal distribution.

There’s actually an entire family of t- distributions. They all have similar formulas (but the math is beyond the scope of this introductory course in statistics), and they all have slightly “fatter tails” than the normal distribution. But some are closer to normal than others.

The t- distributions that have higher “degrees of freedom” are closer to normal (degrees of freedom is a mathematical concept that we won’t study in this course, beyond merely mentioning it here). So, there’s a t- distribution “with one degree of freedom,” another t- distribution “with 2 degrees of freedom” which is slightly closer to normal, another t- distribution “with 3 degrees of freedom” which is a bit closer to normal than the previous ones, and so on.

The following picture illustrates this idea with just a couple of t- distributions (note that “degrees of freedom” is abbreviated “d.f.” on the picture):

The test statistic for our t-test for one population mean is a t -score which follows a t- distribution with (n – 1) degrees of freedom. Recall that each t- distribution is indexed according to “degrees of freedom.” Notice that, in the context of a test for a mean, the degrees of freedom depend on the sample size in the study.

Remember that we said that higher degrees of freedom indicate that the t- distribution is closer to normal. So in the context of a test for the mean, the larger the sample size , the higher the degrees of freedom, and the closer the t- distribution is to a normal z distribution .

As a result, in the context of a test for a mean, the effect of the t- distribution is most important for a study with a relatively small sample size .

We are now done introducing the t-distribution. What are implications of all of this?

• The null distribution of our t-test statistic is the t-distribution with (n-1) d.f. In other words, when Ho is true (i.e., when μ = μ 0 (mu = mu_zero)), our test statistic has a t-distribution with (n-1) d.f., and this is the distribution under which we find p-values.
• For a large sample size (n), the null distribution of the test statistic is approximately Z, so whether we use t(n – 1) or Z to calculate the p-values does not make a big difference.

Talk to our experts

1800-120-456-456

• Conditional Statement

What Is A Conditional Statement?

In mathematics, we define statement as a declarative statement which may either be true or may be false. Often sentences that are mathematical in nature may not be a statement because we might not know what the variable represents. For example, 2x + 2 = 5. Now here we do not know what x represents thus if we substitute the value of x (let us consider that x = 3) i.e., 2 × 3 = 6. Therefore, it is a false statement. So, what is a conditional statement? In simple words, when through a statement we put a condition on something in return of something, we call it a conditional statement. For example, Mohan tells his friend that “if you do my homework, then I will pay you 50 dollars”. So what is happening here? Mohan is paying his friend 50 dollars but places a condition that if only he’s work will be completed by his friend. A conditional statement is made up of two parts. First, there is a hypothesis that is placed after “if” and before the comma and second is a conclusion that is placed after “then”. Here, the hypothesis will be “you do my homework” and the conclusion will be “I will pay you 50 dollars”. Now, this statement can either be true or may be false. We don’t know. 

A hypothesis is a part that is used after the 'if' and before the comma. This composes the first part of a conditional statement. For example, the statement, 'I help you get an A+ in math,' is a hypothesis because this phrase is coming in between the 'if' and the comma. So, now I hope you can spot the hypothesis in other examples of a conditional statement. Of course, you can. Here is a statement: 'If Miley gets a car, then Allie's dog will be trained,' the hypothesis here is, 'Miley gets a car.' For the statement, 'If Tom eats chocolate ice cream, then Luke eats double chocolate ice cream,' the hypothesis here is, 'Tom eats chocolate ice cream. Now it is time for you to try and locate the hypothesis for the statement, 'If the square is a rectangle, then the rectangle is a quadrilateral'?

A conclusion is a part that is used after “then”. This composes the second part of a conditional statement. For example, for the statement, “I help you get an A+ in math”, the conclusion will be “you will give me 50 dollars”. The next statement was “If Miley gets a car, then Allie's dog will be trained”, the conclusion here is Allie's dog will be trained. It is the same with the next statement and for every other conditional statement.   

How Do We Know If A Statement Is True or False? 

In mathematics, the best way we can know if a statement is true or false is by writing a mathematical proof. Before writing a proof, the mathematician must find if the statement is true or false that can be done with the help of exploration and then by finding the counterexample. Once the proof is discovered, the mathematician must communicate this discovery to those who speak the language of maths. 

Converse, Inverse, contrapositive, And Bi-conditional Statement

We usually use the term “converse” as a verb for talking and chatting and as a noun we use it to represent a brand of footwear. But in mathematics, we use it differently. Converse and inverse are the two terms that are a connected concept in the making of a conditional statement.

If we want to create the converse of a conditional statement, we just have to switch the hypothesis and the conclusion. To create the inverse of a conditional statement, we have to turn both the hypothesis and the conclusion to the negative. A contrapositive statement can be made if we first interchange the hypothesis and conclusion then make them both negative. In a bi-conditional statement, we use “if and only if” which means that the hypothesis is true only if the condition is true. For example, 

If you eat junk food, then you will gain weight is a conditional statement.

If you gained weight, then you ate junk food is a converse of a conditional statement.

If you do not eat junk food, then you will not gain weight is an inverse of a conditional statement.

If yesterday was not Monday, then today is not Tuesday is a contrapositive statement. 

Today is Tuesday if and only if yesterday was Monday is a bi-conventional statement.   

Image will be uploaded soon

A Conditional Statement Truth Table

In the table above, p→q will be false only if the hypothesis(p) will be true and the conclusion(q) will be false, or else p→q will be true. 

Conditional Statement Examples

Below, you can see some of the conditional statement examples.

Example 1) Given, P = I do my work; Q = I get the allowance

What does p→q represent?

Solution 1) In the sentence above, the hypothesis is “I do my work” and the conclusion is “ I get the allowance”. Therefore, the condition p→q represents the conditional statement, “If I do my work, then I get the allowance”. 

Example 2) Given, a = The sun is a ball of gas; b = 5 is a prime number. Write a→b in a sentence. 

Solution 2) The conditional statement a→b here is “if the sun is a ball of gas, then 5 is a prime number”.

FAQs on Conditional Statement

1. How many types of conditional statements are there?

There are basically 5 types of conditional statements.

If statement, if-else statement, nested if-else statement, if-else-if ladder, and switch statement are the basic types of conditional statements. If a function displays a statement or performs a function on the condition if the statement is true. If-else statement executes a block of code if the condition is true but if the condition is false, a new block of code is placed. The switch statement is a selection control mechanism that allows the value of a variable to change the control flow of a program. 

2. How are a conditional statement and a loop different from each other?

A conditional statement is sometimes used by a loop but a loop is of no use to a conditional statement. A conditional statement is basically a “yes” or a “no” i.e., if yes, then take the first path else take the second one. A loop is more like a cyclic chain starting from the start point i.e., if yes, then take path a, if no, take path b and it comes back to the start point. 

Conditional statement executes a statement based on a condition without causing any repetition. 

A loop executes a statement repeatedly. There are two loop variables i.e., for loop and while loop.

Become a math whiz with AI Tutoring, Practice Questions & more.

Conditional Statements

Two common types of statements found in the study of logic are conditional and biconditional statements. They are formed by combining two statements which we then we call compound statements. What if we were to say, "If it snows, then we don't go outside." This is two statements combined. They are often called if-then statements. As in, "IF it snows, THEN we don't go outside." They are a fundamental building block of computer programming.

Writing conditional statements

A statement written in if-then format is a conditional statement.

It looks like

This represents the conditional statement:

"If p then q ."

A conditional statement is also called an implication.

If a closed shape has three sides, then it is a triangle.

The part of the statement that follows the "if" is called the hypothesis. The part of the statement that follows the "then" is the conclusion.

So in the above statement,

If a closed shape has three sides, (this is the hypothesis)

Then it is a triangle. (this is the conclusion)

Identify the hypothesis and conclusion of the following conditional statement.

A polygon is a hexagon if it has six sides.

Hypothesis: The polygon has six sides.

Conclusion: It is a hexagon.

The hypothesis does not always come first in a conditional statement. You must read it carefully to determine which part of the statement is the hypothesis and which part is the conclusion.

Truth table for conditional statement

The truth table for any two given inputs, say A and B , is given by:

• If A and B are both true, then A → B is true.
• If A is true and B is false, then A → B is false.
• If A is false and B is true, then A → B is true.
• If A and B are both false, then A → B is true.

Take our conditional statement that if it snows, we do not go outside.

If it is snowing ( A is true) and we do go outside ( B is false), then the statement A → B is false.

If it is not snowing ( A is false), it doesn't matter if we go outside or not ( B is true or false), because A → B is impossible to determine if A is false, so the statement A → B can still be true.

Biconditional statements

A biconditional statement is a combination of a statement and its opposite written in the format of "if and only if."

For example, "Two line segments are congruent if and only if they are the same length."

This is a combination of two conditional statements.

"Two line segments are congruent if they are the same length."

"Two line segments are the same length if they are congruent."

A biconditional statement is true if and only if both the conditional statements are true.

Biconditional statements are represented by the symbol:

p ↔ q

p ↔ q = p → q ∧ q → p

Writing biconditional statements

Write the two conditional statements that make up this biconditional statement:

I am punctual if and only if I am on time to school every day.

The two conditional statements that have to be true to make this statement true are:

• I am punctual if I am on time to school every day.
• I am on time to school every day if I am punctual.

A rectangle is a square if and only if the adjacent sides are congruent.

• If the adjacent sides of a rectangle are congruent then it is a square.
• If a rectangle is a square then the adjacent sides are congruent.

Topics related to the Conditional Statements

Conjunction

Counter Example

Biconditional Statement

Flashcards covering the Conditional Statements

Symbolic Logic Flashcards

Introduction to Proofs Flashcards

Practice tests covering the Conditional Statements

Introduction to Proofs Practice Tests

Get help learning about conditional statements

Understanding conditional statements can be tricky, especially when it gets deeper into programming language. If your student needs a boost in their comprehension of conditional statements, have them meet with an expert tutor who can give them 1-on-1 support in a setting free from distractions. A tutor can work at your student's pace so that tutoring is efficient while using their learning style - so that tutoring is effective. To learn more about how tutoring can help your student master conditional statements, contact the Educational Directors at Varsity Tutors today.

• ASCP Board of Certification - American Society for Clinical Pathology Board of Certification Training
• Holistic Medicine Tutors
• Internal Medicine Tutors
• DAT Courses & Classes
• Haitian Creole Tutors
• North Carolina Bar Exam Courses & Classes
• Actuarial Exam PA Test Prep
• Spanish 3 Tutors
• SSAT Test Prep
• Livonian Tutors
• Computer Programming Tutors
• CISM - Certified Information Security Manager Courses & Classes
• ARM - Associate in Risk Management Courses & Classes
• Arizona Bar Exam Test Prep
• SHSAT Test Prep
• REGENTS Tutors
• Series 57 Tutors
• WEST-E Test Prep
• Honors Science Tutors
• High School Level American Literature Tutors
• Kansas City Tutoring
• Austin Tutoring
• San Francisco-Bay Area Tutoring
• Buffalo Tutoring
• Philadelphia Tutoring
• Louisville Tutoring
• Atlanta Tutoring
• Dayton Tutoring
• San Antonio Tutoring
• Albuquerque Tutoring
• GRE Tutors in Los Angeles
• ACT Tutors in Philadelphia
• LSAT Tutors in Washington DC
• English Tutors in Atlanta
• SSAT Tutors in Los Angeles
• Physics Tutors in Seattle
• French Tutors in Seattle
• SSAT Tutors in Dallas Fort Worth
• ISEE Tutors in Dallas Fort Worth
• English Tutors in San Diego

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

17.6: Truth Tables: Conditional, Biconditional

• Last updated
• Save as PDF
• Page ID 34287

• David Lippman
• Pierce College via The OpenTextBookStore

We discussed conditional statements earlier, in which we take an action based on the value of the condition. We are now going to look at another version of a conditional, sometimes called an implication, which states that the second part must logically follow from the first.

Conditional

A conditional is a logical compound statement in which a statement \(p\), called the antecedent, implies a statement \(q\), called the consequent.

A conditional is written as \(p \rightarrow q\) and is translated as "if \(p\), then \(q\)".

The English statement “If it is raining, then there are clouds is the sky” is a conditional statement. It makes sense because if the antecedent “it is raining” is true, then the consequent “there are clouds in the sky” must also be true.

Notice that the statement tells us nothing of what to expect if it is not raining; there might be clouds in the sky, or there might not. If the antecedent is false, then the consquent becomes irrelevant.

Suppose you order a team jersey online on Tuesday and want to receive it by Friday so you can wear it to Saturday’s game. The website says that if you pay for expedited shipping, you will receive the jersey by Friday. In what situation is the website telling a lie?

There are four possible outcomes:

1) You pay for expedited shipping and receive the jersey by Friday

2) You pay for expedited shipping and don’t receive the jersey by Friday

3) You don’t pay for expedited shipping and receive the jersey by Friday

4) You don’t pay for expedited shipping and don’t receive the jersey by Friday

Only one of these outcomes proves that the website was lying: the second outcome in which you pay for expedited shipping but don’t receive the jersey by Friday. The first outcome is exactly what was promised, so there’s no problem with that. The third outcome is not a lie because the website never said what would happen if you didn’t pay for expedited shipping; maybe the jersey would arrive by Friday whether you paid for expedited shipping or not. The fourth outcome is not a lie because, again, the website didn’t make any promises about when the jersey would arrive if you didn’t pay for expedited shipping.

It may seem strange that the third outcome in the previous example, in which the first part is false but the second part is true, is not a lie. Remember, though, that if the antecedent is false, we cannot make any judgment about the consequent. The website never said that paying for expedited shipping was the only way to receive the jersey by Friday.

A friend tells you “If you upload that picture to Facebook, you’ll lose your job.” Under what conditions can you say that your friend was wrong?

1) You upload the picture and lose your job

2) You upload the picture and don’t lose your job

3) You don’t upload the picture and lose your job

4) You don’t upload the picture and don’t lose your job

There is only one possible case in which you can say your friend was wrong: the second outcome in which you upload the picture but still keep your job. In the last two cases, your friend didn’t say anything about what would happen if you didn’t upload the picture, so you can’t say that their statement was wrong. Even if you didn’t upload the picture and lost your job anyway, your friend never said that you were guaranteed to keep your job if you didn’t upload the picture; you might lose your job for missing a shift or punching your boss instead.

In traditional logic, a conditional is considered true as long as there are no cases in which the antecedent is true and the consequent is false.

Truth table for the conditional

\(\begin{array}{|c|c|c|} \hline p & q & p \rightarrow q \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

Again, if the antecedent \(p\) is false, we cannot prove that the statement is a lie, so the result of the third and fourth rows is true.

Construct a truth table for the statement \((m \wedge \sim p) \rightarrow r\)

We start by constructing a truth table with 8 rows to cover all possible scenarios. Next, we can focus on the antecedent, \(m \wedge \sim p\).

\(\begin{array}{|c|c|c|} \hline m & p & r \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \end{array}\)

\(\begin{array}{|c|c|c|c|} \hline m & p & r & \sim p \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

\(\begin{array}{|c|c|c|c|c|} \hline m & p & r & \sim p & m \wedge \sim p \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \end{array}\)

Now we can create a column for the conditional. Because it can be confusing to keep track of all the Ts and \(\mathrm{Fs}\), why don't we copy the column for \(r\) to the right of the column for \(m \wedge \sim p\) ? This makes it a lot easier to read the conditional from left to right.

\(\begin{array}{|c|c|c|c|c|c|c|} \hline m & p & r & \sim p & m \wedge \sim p & r & (m \wedge \sim p) \rightarrow r \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

When \(m\) is true, \(p\) is false, and \(r\) is false- -the fourth row of the table-then the antecedent \(m \wedge \sim p\) will be true but the consequent false, resulting in an invalid conditional; every other case gives a valid conditional.

If you want a real-life situation that could be modeled by \((m \wedge \sim p) \rightarrow r\), consider this: let \(m=\) we order meatballs, \(p=\) we order pasta, and \(r=\) Rob is happy. The statement \((m \wedge \sim p) \rightarrow r\) is "if we order meatballs and don't order pasta, then Rob is happy". If \(m\) is true (we order meatballs), \(p\) is false (we don't order pasta), and \(r\) is false (Rob is not happy), then the statement is false, because we satisfied the antecedent but Rob did not satisfy the consequent.

For any conditional, there are three related statements, the converse, the inverse, and the contrapositive.

Related Statments

The original conditional is \(\quad\) "if \(p,\) then \(q^{\prime \prime} \quad p \rightarrow q\)

The converse is \(\quad\) "if \(q,\) then \(p^{\prime \prime} \quad q \rightarrow p\)

The inverse is \(\quad\) "if not \(p,\) then not \(q^{\prime \prime} \quad \sim p \rightarrow \sim q\)

The contrapositive is "if not \(q,\) then not \(p^{\prime \prime} \quad \sim q \rightarrow \sim p\)

Consider again the conditional “If it is raining, then there are clouds in the sky.” It seems reasonable to assume that this is true.

The converse would be “If there are clouds in the sky, then it is raining.” This is not always true.

The inverse would be “If it is not raining, then there are not clouds in the sky.” Likewise, this is not always true.

The contrapositive would be “If there are not clouds in the sky, then it is not raining.” This statement is true, and is equivalent to the original conditional.

Looking at truth tables, we can see that the original conditional and the contrapositive are logically equivalent, and that the converse and inverse are logically equivalent.

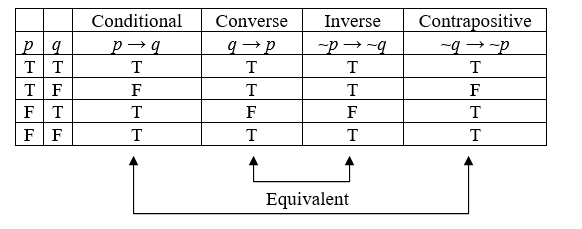
Equivalence

A conditional statement and its contrapositive are logically equivalent.

The converse and inverse of a conditional statement are logically equivalent.

In other words, the original statement and the contrapositive must agree with each other; they must both be true, or they must both be false. Similarly, the converse and the inverse must agree with each other; they must both be true, or they must both be false.

Be aware that symbolic logic cannot represent the English language perfectly. For example, we may need to change the verb tense to show that one thing occurred before another.

Suppose this statement is true: “If I eat this giant cookie, then I will feel sick.” Which of the following statements must also be true?

• If I feel sick, then I ate that giant cookie.
• If I don’t eat this giant cookie, then I won’t feel sick.
• If I don’t feel sick, then I didn’t eat that giant cookie.
• This is the converse, which is not necessarily true. I could feel sick for some other reason, such as drinking sour milk.
• This is the inverse, which is not necessarily true. Again, I could feel sick for some other reason; avoiding the cookie doesn’t guarantee that I won’t feel sick.
• This is the contrapositive, which is true, but we have to think somewhat backwards to explain it. If I ate the cookie, I would feel sick, but since I don’t feel sick, I must not have eaten the cookie.

Notice again that the original statement and the contrapositive have the same truth value (both are true), and the converse and the inverse have the same truth value (both are false).

Try it Now 5

“If you microwave salmon in the staff kitchen, then I will be mad at you.” If this statement is true, which of the following statements must also be true?

• If you don’t microwave salmon in the staff kitchen, then I won’t be mad at you.
• If I am not mad at you, then you didn’t microwave salmon in the staff kitchen.
• If I am mad at you, then you microwaved salmon in the staff kitchen.

Choice b is correct because it is the contrapositive of the original statement.

Consider the statement “If you park here, then you will get a ticket.” What set of conditions would prove this statement false?

• You don’t park here and you get a ticket.
• You don’t park here and you don’t get a ticket.
• You park here and you don’t get a ticket.

The first two statements are irrelevant because we don’t know what will happen if you park somewhere else. The third statement, however contradicts the conditional statement “If you park here, then you will get a ticket” because you parked here but didn’t get a ticket. This example demonstrates a general rule; the negation of a conditional can be written as a conjunction: “It is not the case that if you park here, then you will get a ticket” is equivalent to “You park here and you do not get a ticket.”

The Negation of a Conditional

The negation of a conditional statement is logically equivalent to a conjunction of the antecedent and the negation of the consequent.

\(\sim(p \rightarrow q)\) is equivalent to \(p \wedge \sim q\)

Which of the following statements is equivalent to the negation of “If you don’t grease the pan, then the food will stick to it” ?

• I didn’t grease the pan and the food didn’t stick to it.
• I didn’t grease the pan and the food stuck to it.
• I greased the pan and the food didn’t stick to it.
• This is correct; it is the conjunction of the antecedent and the negation of the consequent. To disprove that not greasing the pan will cause the food to stick, I have to not grease the pan and have the food not stick.
• This is essentially the original statement with no negation; the “if…then” has been replaced by “and”.
• This essentially agrees with the original statement and cannot disprove it.

Try it Now 6

“If you go swimming less than an hour after eating lunch, then you will get cramps.” Which of the following statements is equivalent to the negation of this statement?

• I went swimming more than an hour after eating lunch and I got cramps.
• I went swimming less than an hour after eating lunch and I didn’t get cramps.
• I went swimming more than an hour after eating lunch and I didn’t get cramps.

Choice b is equivalent to the negation; it keeps the first part the same and negates the second part.

In everyday life, we often have a stronger meaning in mind when we use a conditional statement. Consider “If you submit your hours today, then you will be paid next Friday.” What the payroll rep really means is “If you submit your hours today, then you will be paid next Friday, and if you don’t submit your hours today, then you won’t be paid next Friday.” The conditional statement if t , then p also includes the inverse of the statement: if not t , then not p . A more compact way to express this statement is “You will be paid next Friday if and only if you submit your timesheet today.” A statement of this form is called a biconditional .

Biconditional

A biconditional is a logical conditional statement in which the antecedent and consequent are interchangeable.

A biconditional is written as \(p \leftrightarrow q\) and is translated as " \(p\) if and only if \(q^{\prime \prime}\).

Because a biconditional statement \(p \leftrightarrow q\) is equivalent to \((p \rightarrow q) \wedge(q \rightarrow p),\) we may think of it as a conditional statement combined with its converse: if \(p\), then \(q\) and if \(q\), then \(p\). The double-headed arrow shows that the conditional statement goes from left to right and from right to left. A biconditional is considered true as long as the antecedent and the consequent have the same truth value; that is, they are either both true or both false.

Truth table for the biconditional

\(\begin{array}{|c|c|c|} \hline p & q & p \leftrightarrow q \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

Notice that the fourth row, where both components are false, is true; if you don’t submit your timesheet and you don’t get paid, the person from payroll told you the truth.

Suppose this statement is true: “The garbage truck comes down my street if and only if it is Thursday morning.” Which of the following statements could be true?

• It is noon on Thursday and the garbage truck did not come down my street this morning.
• It is Monday and the garbage truck is coming down my street.
• It is Wednesday at 11:59PM and the garbage truck did not come down my street today.
• This cannot be true. This is like the second row of the truth table; it is true that I just experienced Thursday morning, but it is false that the garbage truck came.
• This cannot be true. This is like the third row of the truth table; it is false that it is Thursday, but it is true that the garbage truck came.
• This could be true. This is like the fourth row of the truth table; it is false that it is Thursday, but it is also false that the garbage truck came, so everything worked out like it should.

Try it Now 7

Suppose this statement is true: “I wear my running shoes if and only if I am exercising.” Determine whether each of the following statements must be true or false.

• I am exercising and I am not wearing my running shoes.
• I am wearing my running shoes and I am not exercising.
• I am not exercising and I am not wearing my running shoes.

Choices a & b are false; c is true.

Create a truth table for the statement \((A \vee B) \leftrightarrow \sim C\)

Whenever we have three component statements, we start by listing all the possible truth value combinations for \(A, B,\) and \(C .\) After creating those three columns, we can create a fourth column for the antecedent, \(A \vee B\). Now we will temporarily ignore the column for \(C\) and focus on \(A\) and \(B\), writing the truth values for \(A \vee B\).

\(\begin{array}{|c|c|c|} \hline A & B & C \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \end{array}\)

\(\begin{array}{|c|c|c|c|} \hline A & B & C & A \vee B \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \end{array}\)

Next we can create a column for the negation of \(C\). (Ignore the \(A \vee B\) column and simply negate the values in the \(C\) column.)

\(\begin{array}{|c|c|c|c|c|} \hline A & B & C & A \vee B & \sim C \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

Finally, we find the truth values of \((A \vee B) \leftrightarrow \sim C\). Remember, a biconditional is true when the truth value of the two parts match, but it is false when the truth values do not match.

\(\begin{array}{|c|c|c|c|c|c|} \hline A & B & C & A \vee B & \sim C & (A \vee B) \leftrightarrow \sim C \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \end{array}\)

To illustrate this situation, suppose your boss needs you to do either project \(A\) or project \(B\) (or both, if you have the time). If you do one of the projects, you will not get a crummy review ( \(C\) is for crummy). So \((A \vee B) \leftrightarrow \sim C\) means "You will not get a crummy review if and only if you do project \(A\) or project \(B\)." Looking at a few of the rows of the truth table, we can see how this works out. In the first row, \(A, B,\) and \(C\) are all true: you did both projects and got a crummy review, which is not what your boss told you would happen! That is why the final result of the first row is false. In the fourth row, \(A\) is true, \(B\) is false, and \(C\) is false: you did project \(A\) and did not get a crummy review. This is what your boss said would happen, so the final result of this row is true. And in the eighth row, \(A, B\), and \(C\) are all false: you didn't do either project and did not get a crummy review. This is not what your boss said would happen, so the final result of this row is false. (Even though you may be happy that your boss didn't follow through on the threat, the truth table shows that your boss lied about what would happen.)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.8: Conditional/Hypothetical Clauses

• Last updated
• Save as PDF
• Page ID 108090

• Don Bissonnette
• South Seattle Community College

Conditional / Hypothetical Sentences

All conditional / hypothetical sentences consist of a dependent clause beginning with if (or other adverbials of condition) and an independent clause which is a result of the condition or hypothesis. A conditional sentence is one that is real or possibly can happen; a hypothetical sentence is one that is only imaginary - it either will not happen or did not happen.

Class One: Conditional

A.   Present or future situation: True and Real or Possible

If + present tense verb,     will or future implied verb ( c an, might, want, need, etc.)

           Examples:

If my sister visits Seattle, I will take her to Mount Rainier.

If we go there, I want to take a picnic lunch.

B.   General Truth situations, not for a specific time, something is always true and never changes.  It is True and Real or Possible

If + present tense verb,     present tense verb

           Examples:

If plants have good soil and get enough sunlight and water, they always grow well.

If a car runs out of gas, it stops.

C.  Past Situations: True and Completed Actions in the Past

Form:    

If + past tense,   past tense

           Examples:

If my father caught fish, he was happy.

If my grandmother cooked dinner when I was a boy, I always ate a lot.  

D.  Alternate Form for the Present and Future Situations : Should

We can use should in Class One conditional sentences in the present and future  when we are not sure of the condition . Only if the condition happens will the result happen. It gives a feeling of uncertainty (not sure of something).

          Examples:

If you should receive a letter from John, please tell me. Should you receive a letter from John, please let me know.

If you should get stopped by a policeman, you must have your driver's license with you or you will get a ticket. Should you get stopped by a policeman, you must have your driver's license with you or you will get a ticket.

Please note that the Class 3, Class 4, and Class 5 conditional/hypothetical  sentences and exercises will be part of the next book in this series (Book Five).

Exercise 43:  Use a class one conditional sentence to combine these sentences, please.  There are different ways to make these sentences.  Remember that if the IF Clause comes first in a sentence, then you MUST use a comma after the IF CLAUSE.

My son won’t go on a picnic with his friends.  It might rain today. My son won’t go on a picnic with his friends if it rains today.

I will buy a new car.  I refuse to spend a lot of money on a car. I will buy a new car if it doesn’t cost too much.

1.  I might fly back to Providence, R.I. this summer.  I have to find a cheap plane ticket.

2.  The student will come to class tomorrow.  She needs to get a ride from her friend.

3.  I might call my sister this evening.  I have to finish my homework early.

4.  My son eats breakfast.  He must have enough time to eat breakfast.

5.  The student is usually late to class.  When he arrives on time, other students are surprised.

6.  Students study in the library.  They need to use the services of the library.

7.  John will take ENG 102 next quarter.  He must pass ENG 101 this quarter.

8.  People are much happier.  The sun comes out in the summer.

9.  Students can study quietly in the library.  Library patrons are quiet in the library.

10.  My son goes to the piano room.  He wants to practice a piece of music.

11.  The woman gets angry very quickly.  People disagree with her.

12.  You can’t get out of jail.  A judge sentences you to jail.

44:  Complete the following sentences, please.

If I have a headache, ….. If I have a headache, I take three aspirins.

1.  I drink coffee in the afternoon, …..

2.  If it is not raining outside when I get home from work, …..

3.  I watch television if …..

4.  If I finish my homework early, …..

5.  My friend eats in the cafeteria if …..

6.  If I have free time, …..

7.  My dog barks if …..

8.  My back hurts if …..

9.  Children don’t go to school in the morning if …..

10.  If people need extra money, …..

11.  I take medicine if …..

12.  Students usually do their homework if …..

13.  If it is raining outside, …..

Exercise 45:  Complete the following sentences with a future meaning verb, please.

If I have homework this evening, ….. If I have homework this evening, I will do it until it is finished.

1.  If I pass the college’s entrance examination,

2.  If we have an examination next week,

3.  If I have to write a composition for next Monday,

4.  If my friend finishes her homework early,

5.  I will begin college classes next quarter,

6.  If we see each other at the market,

7.  If my friend wins the lottery,

8.  If there is something good on TV tonight,

9.  If I am sick tomorrow morning,

10.  If the gas tank on my car reads close to empty,

11.  If students study grammar,

12.  If some visitors come to Seattle for a visit this summer,

13.  If my friend calls me this weekend,

Exercise 46:  Use a class one conditional sentence in the past situations that were real and did happen, please.

Examples:  If I ate too much candy when I was a boy, I threw up .

If I had to go shopping with my sister and my mother when I was a boy, I wanted to go home right away.

1.  If it snowed a lot, my brother, sister, and I ------------------ (go) sledding.

2.  If the weather was nice after school, I ------------------- (walk) home from school.

3.  If there was a cowboy movie on television, I always ------------------ (watch) it.

4.  If my father took my mother shopping, I -------------------- (stay) in the car with him.

5.  If I got good grades on my report card at school, my parents ------------------- (be) very happy.

6.  If my sister cried when she was a little girl, my father -------------------- (comfort) her.

7.  If we took our lunches to school, we -------------------- (not have to) buy lunch.

8.  If we watched scary movies on TV, we -------------------- (have) a hard time falling asleep.

9.  If it was a holiday, our grandfather always -------------------- (give) us some old coins.

10.  If children were bad in school when I was a boy, teachers -------------------- (hit) them without worrying.

11.  If I bought candy with five cents as a boy, I always -------------------- (get) at least five pieces of candy.

12.  If a student fell asleep in class, the teacher ------------------- (slap) the back of his head to wake him up.

13.  If it was a major holiday, my grandmother and mother ------------------- (cook) both Italian food and American food.

14.  If one of my dogs slept in bed with me, my mother ------------------- (yell) at me and the dog.

15.  If my father had a day off from work, we -------------------- (be) very happy.

16.  If my Uncle Carl took me to a baseball game, I -------------------- (eat) a lot of junk food.

17.  If I caught big fish when I went fishing, I always --------------------- (bring) the fish home to eat for dinner.

Exercise 47:  In a class one conditional, change the IF clause to a SHOULD clause, please.

If I see you in class next Friday, I will be happy. 

Should I see you in class next Friday, I will be happy

1. If you win the lottery, you will become very rich.

2.  If it rains next Friday, you will get wet.

3.  If I catch a cold, I might have a runny nose.

4.  If my car breaks down on my way home, I will call Triple A (AAA) for help.

5.  If my son gets a better job, he will make more money.

6.  If my wife plans a barbecue for dinner this Saturday, I will have to do the cooking.

7.  If the Seattle Mariners ever win the World Series in baseball, I will die a happy man.

8.  If I go to Montreal, Canada, for a vacation, I will visit some of my relatives.

9.  If my son Alex comes home for a visit next year, I will be happy to see him again.

10.  If my son André buys a house, we will give him some furniture.

11.  If it rains hard tomorrow, I won’t be able to work in my garden.

12.  If my sister has enough money, she and her son and daughter-in-law will come to Seattle for a vacation next summer.

Class Two: Hypothetical

A.   Present or Future Situations - will not or are not very likely to occur- Not Real, Not Possible,

                                                                                                         Only Imaginary

If + past tense verb,     would or could   + base form of verb

          Examples:

If I had a million dollars, I would go on a long vacation.

If I played professional baseball, I could make a lot of money.

B.  Verb To Be: Were

In Class Two Conditionals, when you need to use the verb To Be , always use were after if . (This is called the subjunctive.)   

If + subject + were ,     would or could + base form of verb.

  Examples:

If I were a bird, I could fly .

If she were my daughter, I would love her like a father.

C.  Alternate Form for Present Hypothetical Situations: Were    

    Were may be used in place of if to form the Class Two Conditionals; however, this is usually only done in very formal situations.

         Were + noun,     would or could + verb stem

                                           or    

Were + subject + infinitive,     would or could + verb stem

          Examples:    

If you were an American, you would not take ESL classes. Were you an American, you would not take ESL classes.

If I were a woman, I could have a baby. Were I a woman, I could have a baby.

If I bought a new car, my wife would be happy. Were I to buy a new car, my wife would be happy.

If I went to Russia, I would visit Moscow. Were I to go to Russia, I would visit Moscow.

Exercise 48:  In this exercise, the hypothetical situation is in the present, but we use the past tense verbs to show that they are not real.  Complete the following sentences, please.

If my father were alive today, ….. If my father were alive today, he would be very proud of his grandchildren.

If I had a new car, ….. If I had a new car, I would not use it as a truck as I now do with my old car.

1.  If I had a million dollars,

2.  If today were Saturday,

3.  If I had more free time in my life,

4.  If it snowed in June,

5.  If you spoke English as well as I do,

6.  If I found $1,000 on the street in a paper bag,

7.  If I were a professional athlete,

8.  If you still lived in your native country,

9.  If I could go anywhere I wanted to on vacation,

10.  If someone put a gun to my head and demanded all of my money,

11.  If you didn’t go to school,

12.  If you were younger,

Exercise 49:  Complete the following sentences, please.

1.  I would learn to play the guitar if

2.  If I had a lot of money,

3.  My friend would speak better English if

4.  If I wrote better,

5.  I would be happier in life if

6.  Some children would do much better in school if

7.  I would get in trouble if

8.  If the electricity went out right now

9.  People would be healthier if

10.  If America didn’t spend so much money on wars around the world,

11.  My life would be much better if

12.  If my sister didn’t smoke cigarettes,

13.  I would go to the doctor if

14.  I could buy anything I wanted to if

15.  If I were president of the United States,  

Exercise 50:  Change the following class two conditional sentences by using WERE to begin the condition, please.

If I saw a ghost, I would be very scared.   Were I to see a ghost, I would be very scared.

If my mother were alive, she would love to listen to my son’s music. Were my mother alive, she would love to listen to my son’s music.

1.  If you were my child, you would speak perfect English.

2.  If I were an airplane pilot, I would fly planes every day.

3.  If my wife were sitting here, she might learn more English grammar.

4.  If today were Sunday, you wouldn’t be in my class.

5.  If I were sick now, I wouldn’t be to class.

6.  If I had a lot of hair, I wouldn’t were a hat.

7.  If my son ate three hamburgers, his stomach would hurt him.

8.  If I lost $1,000 gambling, my wife would kill me.

9.  If I wore dirty shoes in the house, she would kill me again.

10.  If I got a DWI, my wife would kill me a third time.

11.  If I were to shave my beard, my students might not recognize me.

12.  If I had more space, I would write more sentences.

• Math Article

Conditional Statement

In the study of logic, there are two types of statements, conditional statement and bi-conditional statement . These statements are formed by combining two statements, which are called compound statements . Suppose a statement is- if it rains, then we don’t play. This is a combination of two statements. These types of statements are mainly used in computer programming languages such as c, c++, etc. Let us learn more here with examples.

Conditional Statement Definition

A conditional statement is represented in the form of “if…then”. Let p and q are the two statements, then statements p and q can be written as per different conditions, such as;

• p implies q
• p is sufficient for q
• q is necessary for p

Points to remember:

• A conditional statement is also called implication .
• The sign of the logical connector conditional statement is →. Example P → Q pronouns as P implies Q.
• The state P → Q is false if the P is true and Q is false otherwise P → Q is true.

Truth Table for Conditional Statement

The truth table for any two inputs, say A and B is given by;

Example: We have a conditional statement If it is raining, we will not play. Let, A: It is raining and B: we will not play. Then;

• If A is true, that is, it is raining and B is false, that is, we played, then the statement A implies B is false.
• If A is false, that is, it is not raining and B is true, that is, we did not play, still the statement is true. A is the necessary condition for B but it is not sufficient.
• If A is true, B should be true but if A is false B may or may not be true.

What is a Bi-Conditional Statement?

A statement showing an “if and only if” relation is known as a biconditional statement. An event P will occur if and only if the event Q occurs, which means if P has occurred then it implies Q will occur and vice versa.

P: A number is divisible by 2.

Q: A number is even.

If P will occur then Q will occur and if Q will occur then P will occur.

Hence, P will occur if and only if Q will occur.

We can say that P↔Q.

Conditional Statement Examples

Q.1: If a > 0 is a positive number, then is a = 10 correct or not? Justify your answer.

Solution: Given, a > 0 and is a positive number

And it is given a = 10

So the first statement a > 0 is correct because any number greater than 0 is a positive number. But a = 10 is not a correct statement because it can be any number greater than 0.

Q.2: Justify P → Q, for the given table below.

Solution: Case 1: We can see, for the first row, in the given table,

If statement P is correct, then Q is incorrect and if Q is correct then P is incorrect. Both the statements contradict each other.

Hence, P → Q = False

Case 2: In the second row of the given table, if P is correct then Q is correct and if Q is correct then P is also correct. Hence, it satisfies the condition.

P → Q = True

Therefore, we can construct the table;

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.